分割法在高中物理解题中的应用

胡聪明

【摘要】高中物理教学内容是基于初中物理的基础进行的延伸和拓展，并且其中涵盖的抽象内容较多，所以学习难度较大.在实际的高中物理解题过程中，部分题目涵盖了多个知识点内容，所以学生在面对抽象的题目时感到解题困难.因此，综合高中物理解题教学方法和高中学生的物理思维模式，部分高中物理教师提出将分割法运用在物理解题过程中，以此帮助学生简化解题步骤，提高解题效率.在高中物理的解题中运用分割法能够将物理非理想模型转化为物理理想模型，将三维转变为二维，将非线性变量转化为线性变量甚至是恒量，以此简化问题，从而帮助高中学生完成解题.本文将以分割法概念作为切入点，然后分析分割法在高中物理解题中的意义，最后以实际题目为例分析分割法的运用.

【关键词】分割法;高中物理;解題应用

1 分割法概念简述

将研究对象分割成不同组成部分，然后对所有局部求和，这种方法称为分割法.这个方法的核心是简化物理量，把研究对象向已知物理量进行切割，将整体分割为若干个子对象，并将研究目的转变为若干个子目的，因此便于计算衡量，从而解决问题.在高中物理解题过程中运用分割法可以将一个独立的、完整的物体分割成若干部分，并且可以根据题干内容、题目要求采取多种多样的分割方式.

在高中物理解题教学或者实验教学中采取分割法可以以时间为单位对图像、对象、位移、轨迹进行分割，以此将陌生的问题转变为常规问题，降低题目难度系数，从而进行解答，因此，切割法在高中物理教学过程中是一种常见的思维方法.

2 分割法在高中物理解题中的意义

2.1 阐明物理规律

运用分割、填补的手段能够促使事物的特点发生变化，从而帮助学生明确物理规律，有助于学生深入了解物理知识.

例如 在高中物理力学教学篇章中，许多高中物理教师会通过独轮车、阿基米德“撬动地球”等内容引入杠杆原理.但是由于现阶段的高中学生对独轮车印象浅薄，也对“撬动地球”的说法感到夸张，不明确杠杆原理的受力点，导致对力学知识点内容模糊.因此，在教学过程借助多媒体设备为学生展示“切割独轮车”的动态图像，将独轮车切割为车身和车轮两部分，便能够直观地向学生阐释物理规律（如下图1所示）.

除此之外，在力学的教学过程中可以借助积木等教学用具制作独轮车的车身、车轮模型，并且通过拆分积木引导学生明白杠杆原理.

2.2 分析实验现象

纵观高中教育课程，物理课程教学过程中会涉及到大量的物理实验，而现阶段高中学生所接触到的物理规律都是经过大批物理学家所参与、设计、制作的物理实验进行分析总结而得出的.在高中物理教学过程中，物理实验也是受教者和教学者利用教学工具再现物理现象，有目的地开展物理教学工作的方法.

例如 高中物理《光的折射和全反射》的教学过程中，虽然本篇章中“光的折射”内容在初中物理教学中已经有所涉及，但是仍有部分同学对光的折射的概念产生混淆.因此在教学过程中通过设计“光的折射”实验，引导学生通过实验现象明确概念.

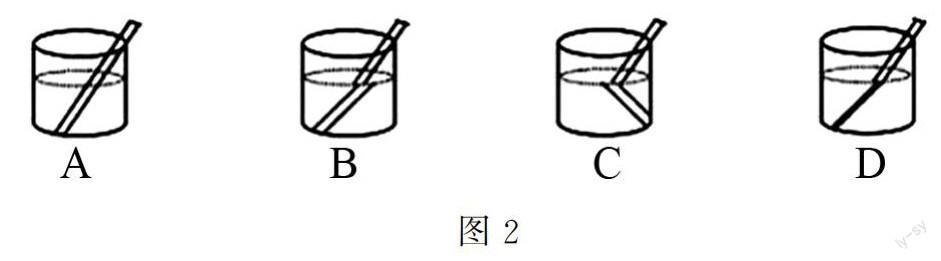
例如 在教学过程中通过多媒体课件展示以下图像，引导学生对光的折射进行思考.（如下图2所示）

在解题过程中，通过利用分割法将图中杯子上半部分和下半部分进行切割，玻璃杯和水相当于放大镜，所以水中的筷子被放大，所以B选项正确.在面对部分具有实验现象和实验特征的题目中采用分割法能够帮助学生明确了解物理量的作用，从而帮助答题.

3 分割法在高中物理解题中的应用

3.1 在重力计算中的应用

力学作为高中物理教育阶段的重点内容，也是高考的热门考点，所以结合重力计算题目，采用分割法能够发挥分割法的直观性优势，帮助学生进行解题.以下题为例：

例题1 A、B两个质点的质量分别为m_A和m_B，两个质点之间以一个不计质量的轻杆进行连接，再一细线连接A点，可促使该结构在悬挂过程中处于平衡状态.当杆沿处于竖直静止状态后，该系统的中心在杆的直线上，再将杆与C点进行连接，保证该结构处于平衡状态，那么点C就是该结构的重心（如下图3所示），求解重心.

那么根据G_A·AC=G_B·BC

将重心问题带入到直角坐标系当中，得出图3，根据杠杆原理可得重心C的坐标：

x_C=G_Ax_A+G_Bx_BG_A+G_B，

y_C=G_Ay_A+G_By_BG_A+G_B，

若两个质点质量相同，则质点连线中点为重心;若两个质点质量不同，则重心向重量较大的一方偏移.

分析 在高中物理力学的解题过程中，对部分求重心、质心的题目会采用定义法、负质量法等，其中定义法更加常见，但是对于题目中出现质量连续分布的物体，题目难度加大，采用定义法会感到较为困难;而负质量法的本质就是在分割法的基础之上，将物体分割成若干个子部分，继而对重心进行推论.

3.2 在定性分析中的应用

在高中物理解题过程中，定性分析是在研究对象所拥有的本质基础之上对其进行研究，总而言之是在解题过程中运用归纳、整合、概括等方法对题干内容中所表示的条件进行思维加工，从而得出物理规律的本质.因此，在此类题目解题过程中运用分割法能够帮助学生利用已知的事物本质对题干内容进行分析，然后进行加工得出答案，以下题为例：

例题2 如图4所示，原来静止的圆形线圈通以逆时针方向的电流I，在其直径AB上靠近B点放置一根垂直于线圈平面的固定不动的长直导线，并通以电流I′，则圆形线圈将如何转动？

分析 通过对题干已知信息的抓取分析得出该题主要考察了学生的右手螺旋定则和左手定则的掌握情况.在此类题目当中，教师通常引导学生利用微元法和分割法等方法进行解答.在使用微元法进行解答的过程中，以左手定则判断安培力的方向，然后可得直线电流在A点的上的磁场方向是竖直向上且平行于A点电流方向，所以A点不受安培力的影响.然后根据电流的方向进行分析，电流在磁场的影响作用下方向是斜向上运动的，根据右手螺旋定则和左手定则能够了解微元会受到安倍力的影响.综上所述可得该圆形线圈是根据AB为轴进行轴转动;同样，利用分割法对该题目进行解答时，假设将该圆形线圈进行切割，取与直径AB相对称的小段，并画出直导线所产生的磁场，根据安倍定则则可得出同样的结论.

3.3 在定量分析中的应用

在高中物理解题过程中的定量分析是通过物理题目中已有的对象数据或者对象性质之间的数据关系对其进行分析;除此之外，也可以是对不同的对象中所存在的相同性质、相互关系进行数量比较，比较得出的最终结果也将以数量的方式进行呈现.在高中物理定量分析中采用分割法能够将物体的整体数据分割成若干个子数据，从而帮助解答，以下题为例：

例题3 如下图5所示，某个力F=10N作用于半径为R=1m的转盘的边缘上，力F的大小保持不变，但方向始终与作用点的切线方向一致，则转动一周该力所做的功为多少？

分析 这道题考查的是匀速圆周运动和功的计算.在恒力作用下，力做的功为W=Fx所以求出在力作用下通过的位移即可知道答案.然而这道题中，力F沿着作用点的切线方向不断改变方向，属于变力做功，所以不能用W=Fx，直接求解.所以需要通过先计算力F转动一周的位移：x=2πR=2π，再计算力F的位移为：W=Fx=10×2πR=20πJ.在运用分割法进行解答过程中首先将F的运动轨迹进行分割，分割成无限个小段，那么在转动一周的情况下，F的作用点位移与转动的轨迹重合，那么在每一个小段上F所做的功为△W=F△s，那么得出同样答案.

3.4 在电场分析中的应用

在高中物理的教学内容中，电场分析可谓是教学的重点，同样也是高考的重点考核部分.从现行高中物理教材的电学内容进行分析，其中涵盖了电场的能的性质、电场的力的性质、带电粒子的运动等.而近年来高考中所出现的电学题目复杂，对学生的逻辑思维能力有着较高的要求，往往一道题目会考核多个知识点.而在高中物理电场分析题目解答中运用分割法能够将题干内容进行细化，帮助学生逐一攻克难点，以下题为例：

例题4 ab是长为l的均匀带电细杆，P₁、P₂是位于ab所在直线上的连点，位置如图6所示，ab上电荷产生的静电场在P₁处，场强大小为E₁，在P₂处的场强大小为E₂，则下列说法正确的是（）

（A）两处的电场方向相同，E₁>E₂.

（B）两处的电场方向相反，E₁>E₂.

（C）两处的电场方向相同，E₁2