初中数学中关于“圆”的解题策略
2022-05-30阿班
阿班


【摘要】在初中数学知识学习的过程中,“圆”的解题特征具有较强的灵活性及多解性,致使学生在解题过程中容易出现错误.因此,为避免这一现象,教师可以从圆的基础定理入手,启发学生对圆的引申知识进行创新、探究和思考,激发学生对关于“圆”知识内容的进一步学习.同时,教师还应引导学生遵循数学知识的一般学习规律和解题习惯学习“圆”的内容,让学生学会对“圆”知识内容的活学活用,提高学生的解题能力,本文就此展开论述.
【关键词】初中数学;圆;解题策略
1 前言
作为初中数学中的一项主要学习内容,“圆”的知识点学习内容能够影响到学生未来的数学学习,是一种基础性较强的知识内容.为使学生对“圆”知识点的内容高效理解,教师应结合考试题型对学生开展“圆”知识内容的教学引导,使学生能够理解圆的对称性、圆周角及圆的辅助线知识内容,提高学生的解题能力,使枯燥内容能够变得形象易懂,以此提高学生的数学知识核心素养.
2 以圆的基本定理归纳题型
传统层面的一题一分析学习模式,其教学效率不高,且难以提高学生的解题能力.所以,教师可以结合圆的基本定理,引导学生分析圆的知识内容,以此提高学生的数学问题思辨素养.
圆周角的定理是指:在圆周的顶点上,且两边为圆的两条弦的角,即圆上有圆周角的顶点,等弧或同弧对应的圆周角,都与这条弧对应的圆心角的一半相等.在关于圆周角的计算题、证明题解题方面,若从圆周角及圆心角方面开展思考,都可以便捷地找到解题思路,进而缩短学习时间.
在开展解题的过程中,以“圆的认识与圆的对称性”为例,本知识点的学习基本内容为,理解圆的对称性,圆是由无数条对称轴组成的,每一条经过圆心的直线都是其对称轴.还应学习垂径定理内容,与弦的直径平分且垂直,且弦对应的两条弧平分.
在对此问题进行解决的过程中,教师应启发学生先思考圆周角定理,并要求学生掌握圆心角、弦、弧之间的关系,掌握垂径定理并以定理进展证明,对圆的旋转不变性进行理解.
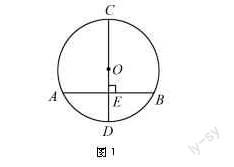
例如 在⊙O中,AB是弦,直径为CD,假如AB⊥CD于E,那么AC=BC,AD=BD.(见图1)
通过本案例推论垂径定理,对于一条直线及一个圆而言,只要具备五条定理中的两条,就能将其他三条定理推导出来,五条定理分别为:与弦垂直、过圆心、平分弦、平分弦所对的劣弧、平分弦所对优弧.结合教材层面的定义进行推论,平分弦(非直径)的直径与弦垂直,且将弦所对应的弧平分.同时,圆也是中心对称图形,圆心是其对称中心,圆还具有旋转不变性.
例1 在⊙O中,AB与⊙O相交于C、D,且BD=AC,那么,OB=OA吗?说出理由.
在这道例题中,教师可以引导学生思考,过点O作AB⊥OE于E,所以DE=CE,又因为BD=AC,所以BE=AE,因此,OE是AB的中垂线,而根据圆的垂线定理可知,中垂线上的任意一点,到线段两端的距离相等,所以OB=OA.
例2 有两个同心圆以O为圆心,大圆的弦AB与小圆相交于两点C、D,求证,AC=BD.(见图2)
证明 过O作AB⊥OE,结合垂径定理进行分析,垂直于弦的直径不仅能将弦平分,也能将这条弦所对应的两条弧平分,则AB被OE平分,CD也被OE平分,因此,DE=CE、BE=AE.又因为BE-DE=BD、AE-CE=AC,所以BE-DE=AE-CE,即BD=AC.
例3 ⊙O的弦CD和直径AB在E点相交,∠CEA=30°,EB=2cm,AE=6cm,求CD的长度.(见图3)
在解决本题的过程中,需要明确此题是利用垂径定理开展的计算问题,在求相关的半径、弦长、弦心距等问题的过程中,通常都会对半径和弦心距构成的直角三角形问题进行求解,而單纯应用“相交弦”定理解决此题会存在一定的难度.
因此,应充分利用已知条件∠BED =30°,构造出一个以半弦、半径、弦心距组成的直角三角形,在对直角三角形问题进行求解后,能够求出未知量[2].
解析 过O作CD⊥OF于点F,将OF、CO连接,因为EB=2,AE=6,所以AB=8,所以OE=AE-OA=2,OC=OA=12AB=4,
又因为在Rt△OEF中,∠AEC=30°,所以OF=12OE=1.
又因为在Rt△COF中,OF=1,OC=4,所以CF=x= 15,又因为CD⊥OF,所以DF=CF,所以CD=2 15.
3 以圆周角开展题型练习
通过案例分析圆形的解题步骤,深入地帮助学生理解圆形问题,提高学生的解题能力.在相关圆的知识点学习过程中,应明确的是其中还包括圆周角计算题目,在实际进行解题的过程中,这类题目多以填空题、选择题的形式出现.在解决此类问题的过程中,学生可以通过一定的解题技巧解决问题,尽量以最短的时间完成解题内容,以此提高解题效率.
在进行解题环节,学生可以结合题目中圆周角以及其所对应的圆心角、弦、弧进行解题,可以通过典型案例讲解法,并通过让学生完成大量练习的方式,增加对本知识内容的记忆.
教师可以启发学生先分析例题,再开展练习,使学生能够在教师指导的方法下做题,使学生的解题熟悉度得以增加.学生在掌握了基本学习方法后,教师应对学生进行深入引导,要求学生模拟教师的计算方法,并尝试将题目的答案在练习纸上进行分析、演练.
例4 在⊙O上分别有点A、B、C,∠AOB=72°,则∠ACB等于( )
(A)36°. (B)18°. (C)54°. (D)28°.
解析 根据圆周角定理可以对这一问题进行解题,圆周角定理反映的是圆心角与圆周角的关系,指的是一条弧所对应的圆周角,与它所对应的圆心角的一半相等,且等弧或同弧对应的圆周角相等[3].根据圆周角定理进行确定,当∠AOB=72°的时候,∠ACB=36°,因此,这道填空题的答案为(A)(见图4)
例5 若⊙O的直径为AB,AC=AB,∠ABE=45°,AC在⊙O的E点上相交,BC在⊙O的D点上相交.需要对∠EBC的度数进行计算,以及对CD=BD进行求证.(见图5)
本题考查的是等腰三角形三线合一定理、等腰直角三角形的性质和判定、圆周角定理等知识,解题的关键点是应对相对应角的度数问题进行解答.
解析 本题中圆的直径为AB,由于∠AEB=90°,∠ABE=45°,AC=AB,进而∠ACB=∠ABC,而这些已知条件是求∠EBC的关键点.将AD连接,由于∠ADB=90°,AC=AB,根据等腰三角形三线合一定义可知CD=BD.
解问题1,将AD连接,因为⊙O的直径为AB,所以AC⊥BE,BC⊥AD,因为∠ABE=45°,∠A=45°,又AB=AC,所以∠CAD=∠BAD=22.5°,所以∠CAD=∠EBC=22.5°.
解问题2,因为BC⊥AD,AC=AB,所以CD=BD.
例6 (见图6)已知△ABC,以AB为直径的⊙O分别交BC于E,交AC于D,连接ED,若EC=ED.
(1)求证:AB=AC;
(2)若AB=4,BC=23,求CD的长.
本题考查的是学生是否能够以圆周角定理及勾股定理分析问题,以此提高学生的圆形知识应用能力.
解 将BD连接,因为AB为直径,所以AC⊥BD,设CD=a,由于AB=AC=4,则AD=4-a,可以通过勾股定理分析此题,将半径、弦心距、半弦三者在同一个直角三角形中进行分析,比如,Rt△CBD中,BD2=BC2-CD2=(23)2-a2,所以(23)2-a2=42-(4-a)2,整理可得,a=32,即CD=32.
4 以圆的辅助线开展题型交流
圆的知识涉及到的知识点较多,且关于圆的题目涵盖基础题、综合题等.学生在学习基础题目的过程中,大都能轻松地完成试题内容,但进入综合题学习阶段,学生的学习不足就会凸显出来.为突破这一现象,教师可有计划对对学生进行教学引导,圆类的知识点中涵盖函数、直线与圆等知识,这类知识点问题复杂,需要辅助线进行辅助教学,但学生大都对辅助线类的知识存在学习难度.教师可以通过题型交流的方式,总结出辅助线的添加方式,以此提高学生的解题能力.
比如,在解決弦的问题过程中,通常需要作出圆心到弦的垂线段,这是一种辅助线即弦心距,主要是为了通过垂径定理,获得平分弦的条件,也是为了通过对直角三角形的构造,结合勾股定理的方式解题.
再比如,在解决同弧或等弧问题的环节,常连等弧对应的圆心角.在解决上述数学问题的过程中,可以通过辅助线的方式完成.
再比如,在学习已知弦中点时常连弦心距的过程中,也应通过辅助线的方式开展教学.
5 结语
综上所述,虽然圆形是一笔形成的图形,貌似很简单,实则却蕴含了丰富的内容.而圆也是一种最基本的平面图形,关于圆的题目,教师可以引导学生通过学习圆的基本定理、圆周角及画辅助线的方式启发学生学习,这会简化学习难度.同时,“圆”知识点的教学目的还在于提高学生的逻辑思维素养及数学知识的综合运用能力,教师可以通过引导学生解题的方式,帮助学生对更多的关于圆的图形问题进行练习,在完成习题的过程中,理解圆的定理,从而实现逐步提高数学综合能力的目的.
参考文献:
[1]张长新.九年级数学中关于“圆”的解题策略教学[J].科学咨询(教育科研),2020(08):279.
[2]蓝奇灵.初中数学教学中几何画板的应用[J].科学咨询(教育科研),2020(06):273.
