基于离散加筋理论的加筋圆柱壳轴压后屈曲缩尺模型研究

李正良 王静超 于伟 朱万旭

摘 要：針对新型干式煤气柜柜体（大型薄壁纵环离散加筋圆柱壳）轴压后屈曲的缩尺模型设计和相似预报问题，基于离散加筋理论与结构体系的总能量推导出结构轴压后屈曲的广 义相似条件和缩尺原理公式.对含不同初始缺陷类型和模型材料的纵环加筋圆柱壳，开展轴 压后屈曲不完全相似模拟研究.研究表明：纵环加筋圆柱壳缩尺模型的轴压后屈曲特性，结合 结构轴压后屈曲不完全相似的相应缩尺原理公式，能较好地预测其原型结构轴压后屈曲的结果.当模型与原型的材料泊松比相同时，模型能准确预测其原型的轴压后屈曲特性.随着模型 与原型的材料泊松比偏差增大，预测原型的后屈曲特性与其原型结果的偏差逐渐增大.提出的缩尺模型设计方法和缩尺原理公式，适用于不同初始缺陷类型和模型材料的纵环加筋圆柱 壳轴压后屈曲相似预报，为实际工程中类似结构轴压后屈曲缩尺模型设计和试验提供参考.

关键词：薄壁结构;气柜;离散加筋理论;后屈曲;缩尺模型

中图分类号：TU33  文献标志码：A

Study on Post-buckling Scalemodel of Stringer Stiffened-cylindrical Shells under Axial Compression Based on Discrete Stiffenedmethod

LI Zhengliang1，2，WANG Jingchao1，YU Wei3，4?，ZHU Wanxu3，4（1.School of Civil Engineering，Chongqing University，Chongqing400045，China;

2.Key Laboratory of New Technology for Construction of Cities inmountain Area（Chongqing University）of theministry of Education，Chongqing400045，China;

3.College of Civil and Architecture Engineering，Guilin University of Technology，Guilin 541004，China;

4.Guangxi Key Laboratory of New Energy and Building Energy Saving，Guilin University of Technology，Guilin 541004，China）

Abstract：Aiming at the scalemodel design and similarity prediction of the buckling of the new typical gas holders body（large thin-walled ring and stringer stiffened-cylindrical shell）under axial compression， general si-militude requirements and scaling laws of stiffened shells under axial compression are presented based on the dis-crete stiffenedmethod and the total energy of the structural system.For the ring and stringer stiffened-cylindrical shells with different initial imperfections andmodelingmaterial properties， the partial similitude of the post-buckling behaviors under axial compression ismainly investigated.The results show that： using partial similitude scaling laws for the post-buckling of stiffened cylindrical shells under axial compression， scaledmodels can accurately predict the post-buckling behaviors of prototypes of discretely ring and stringer stiffened-cylindrical shells under axial com-pression.When thematerial Poisson's ratio of themodel and the prototype is the same， themodel can accurately pre-dict the post-buckling behaviors of the prototype under axial compression.As thematerial Poissons ratio deviation between themodel and the prototype increases， the deviation of the post-buckling behaviors between the predicted prototype and its corresponding prototype gradually increases.In conclusion， the designmethod of scalemodels and scale laws are suitable for the similarity prediction of the post-buckling behaviors of discretely ring and stringer stiffened-cylindrical shells with different initial imperfections andmaterial properties， which provides a reference for the scalemodel design and test of similar structures in practical engineering.

Key words：thin-walled structures;gas holder;the discrete stiffenedmethod;post-buckling;scaledmodel

新型干式煤气柜是一种可储存可燃气体，是能节约能源和保护环境的大型重要构筑物[1].新型干式 煤气柜柜体作为一种典型的大型薄壁纵环离散加筋圆柱壳，由于试验条件和经费的限制，很难对其进行大量的原型结构试验.目前，较为可行的研究方法是 采用缩尺模型的试验结果结合相似理论预测原型的屈曲承载能力.因此，研究纵环加筋圆柱壳轴压后屈 曲缩尺模型的设计方法和相似原理，对验证与评估新型干式煤气柜柜体合理性和安全性显得尤为重要.

杨金花等[2]研究了具有环向贯穿脱层圆柱壳的屈曲问题，讨论了脱层大小、深度、位置以及复合材料纤维铺层方向对脱层圆柱壳屈曲载荷的影响.结果表明：脱层长度越大、越靠近壳的外表和轴向中心，结构的屈 曲 载 荷 越低.向 红 等[3]根据Von K-arman板理论，建立了具损伤正交各向异性板的非线性压曲方程.Singhatanadgid和Ungbhakorn[4]针对压 扭组合荷载作用下的正交各向异性圆板，进行了线性屈曲完全相似和不完全相似研究.结果表明：完全相似模型和采用各向同性材料的不完全相似模型，结合缩尺原理公式，可以较好地预测其原型的屈曲 特性，缩尺原理公式适用于具有任意相同边界条件的一对模型和原型.Hilburger等[5-6]考虑加筋圆柱壳 焊接缺陷的影响，根据结构的半径与等效厚度比值相等的原则，采用密加筋理论、有限元法和结构试验相结合的手段，对缩尺模型与原型进行了稳定性设计和试验，验证了新方法的正确性;同时给出了加筋圆柱壳模型详细和实用的设计方法，但尚未给出缩 尺模型与原型的屈曲相似关系.贾冬云等[7-8]采用理 论分析、有限元模拟和试验研究相结合的方法，对大型正多边形煤气柜立柱、加筋肋和壁板进行了系統的研究.总体而言，现有研究可以解决层合壳、板和密加筋圆柱壳屈曲的缩尺模型设计与相似预报问题，但对于纵环离散加筋圆柱壳屈曲相似的研究颇为缺乏，所以开展基于离散加筋理论的纵环加筋圆 柱壳轴压后屈曲缩尺模型研究非常有必要.

本文以纵环加筋圆柱壳为研究对象，基于离散 加筋理论与结构体系的总能量，推导出结构轴压后屈曲的广义相似条件与缩尺原理公式.基于酒窝缺 陷和焊缝缺陷的函数，建立了含初始缺陷的纵环加筋圆柱壳有限元模型.最后，对含初始缺陷的纵环加筋圆柱壳，开展轴压后屈曲不完全相似模拟研究，以验证缩尺模型设计的广义相似条件和轴压后屈曲缩 尺原理公式的准确性.

1基于离散加筋理论的加筋圆柱壳轴压后屈 曲缩尺原理

1.1纵环离散加筋圆柱壳轴压后屈曲的广义相似 条件

在相似转换过程中，相似结构体系的数学模型 是一致的.因此，任意两相似结构体系总能量间的关系可表示为：

式中：下标 p和m分别代表原型和模型;Xpi和Xmi（i=1，2，…，n）分别对应原型结构和模型结构的几何参 数和材料参数;ψ（Ci）（i=1，2，…，n）为两相似结构参 数的传递函数.根据该函数关系可推导出结构的屈 曲缩尺原理公式.

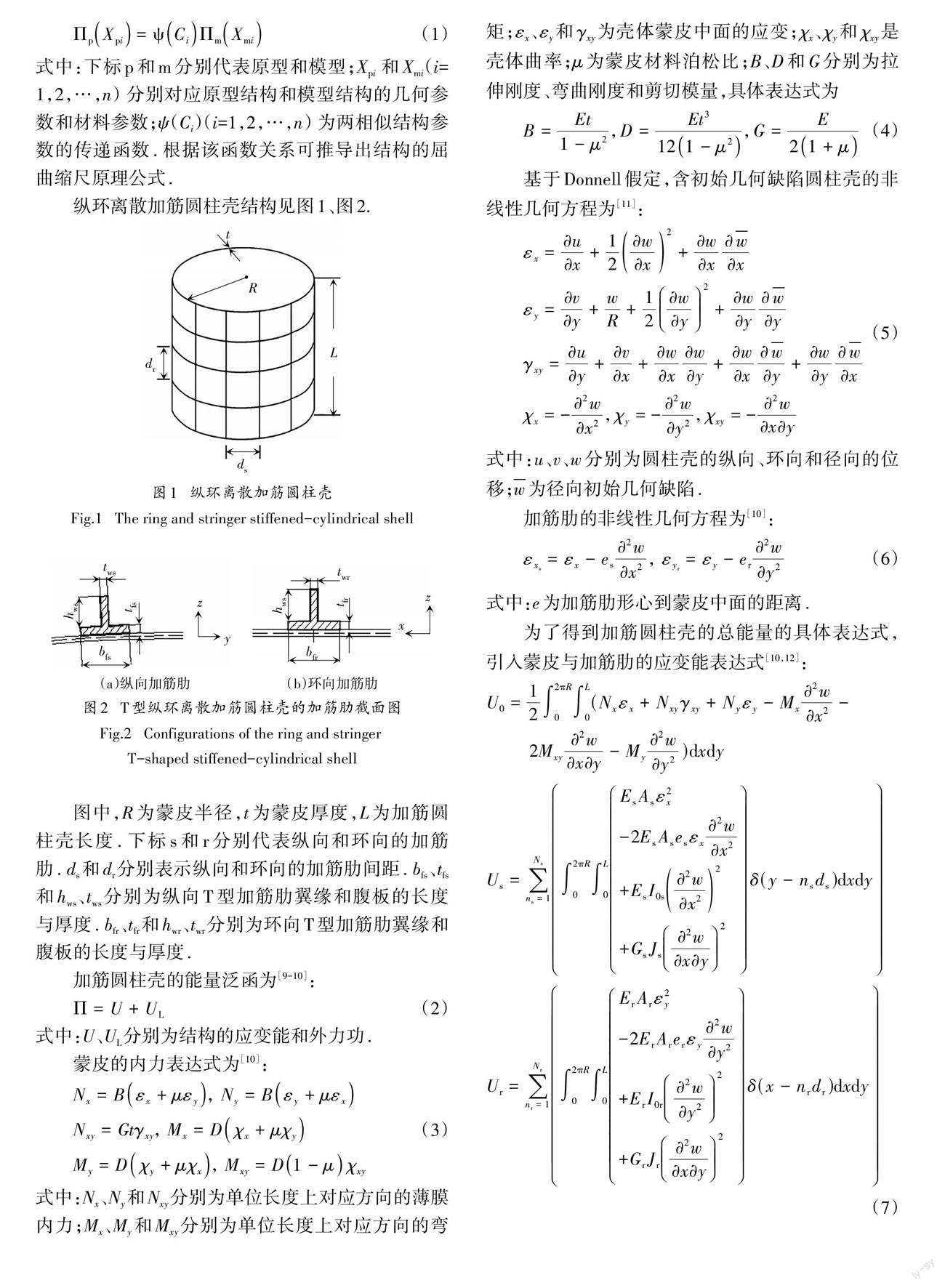
纵环离散加筋圆柱壳结构见图1、图2.

图中，R为蒙皮半径，t为蒙皮厚度，L为加筋圆 柱壳长度.下标 s和r分别代表纵向和环向的加筋肋.ds和dr分别表示纵向和环向的加筋肋间距.bfs、tfs和hws、tws分别为纵向 T型加筋肋翼缘和腹板的长度与厚度.bfr、tfr和hwr、twr分别为环向 T型加筋肋翼缘和腹板的长度与厚度.

2算例验证

基于现有文献中的模型，建立相同参数的有限 元模型进行屈曲分析，并对比它们的屈曲荷载间的误差，有效验证了建立的含初始缺陷的光滑圆柱壳有限元模型的准确性.基于ANSYS 软件建立有限元 模型，模型采用shell181单元，该单元为四节点六自由度单元，计算时间短，精度高.

2.1含酒窝缺陷光滑圆柱壳轴压后屈曲验证

采用文献[15]中含酒窝缺陷光滑圆柱壳轴压后屈曲的算例进行有限元模型验证.结构上端面承受 轴压荷载，下端面固支，上端面仅放松轴向位移自由度.材料和几何参数为：E=72 GPa、μ =0.31、R=0.25m、L=0.51m和t=0.000 5m.在结构高度方向 L/2位置施加酒窝缺陷，缺陷函数[15]见式（23）.

式中：s为缺陷范围内有限元网格节点到缺陷中心的距离;λ和δ0分别为酒窝缺陷的直径与中心幅值;θ和z1分别为光滑圆柱壳的环向和轴向的坐标;θ0和z0分别为酒窝缺陷中心的环向和轴向的坐标.

表1给出含酒窝缺陷光滑圆柱壳轴压后屈曲临 界荷载对比，其中pcr_α 表示文献[15]的临界屈曲荷 载，pcr_FEm表示本文计算的临界屈曲荷载.由结果可 知，不同缺陷半径和不同缺陷幅值工况下，光滑圆柱 壳轴压屈曲临界荷载与文献[15]结果的误差绝对值 均小于8%，表明进行的含酒窝缺陷圆柱壳轴压后屈曲分析准确、可靠.

2.2 含环向焊缝缺陷光滑圆柱壳轴压后屈曲验证

采用文献[16]中的含环向焊缝缺陷光滑圆柱壳 轴压后屈曲的算例进行有限元模型验证.结构两端面承受轴压荷载，上、下端面简支.材料和几何参数为：E=200 GPa、μ=0.3、R=10m、L=30m和t=0.001m.在结构高度方向 L/2位置施加一条环向内陷焊缝，缺 陷函数[16]见式（24）.

式中：λ0为焊缝缺陷半波长.

表2 给出含环向焊缝缺陷光滑圆柱壳轴压后屈 曲临界荷载对比，其中pcr_β 表示文献[16]的临界屈曲 荷载.

从表2可以看出，不同径厚比和环向焊缝不同 缺陷幅值工况下的光滑圆柱壳，其轴压后屈曲临界 荷载与文献[16]结果间的误差绝对值小于10%.同时，屈曲临界荷载处相应结构的屈曲模态环向波数相同.缺陷幅值小于等于1.0t时，误差绝对值在5%以内;当缺陷幅值为1.5t和2t时，误差分别为-7.83%和-9.04%，误差较大的原因可能是现有的板壳后屈 曲分析理论尚不能较好地分析板壳结构缺陷幅值大于1.0t的情况.综上所述，开展的含环向焊缝缺陷光 滑圆柱壳轴压后屈曲分析具有较好的准确性.

3 纵环离散加筋圆柱壳轴压后屈曲不完全相似分析

为了验证所推导的缩尺原理公式的准确性，首 先对纵环加筋圆柱壳缩尺模型和原型进行轴压后屈 曲分析.其次，将缩尺模型的计算结果代入缩尺原理 公式得到原型的预测结果.最后，将预测原型与原型的荷载位移曲线进行对比，并判断它们的屈曲临界 荷载对应的模态是否一致.

纵环加筋圆柱壳原型结构上、下端面简支.蒙皮 与加筋肋的材料参数为：E=200 GPa、μ=0.3.加筋肋 数量为：Ns=8、Nr=2.蒙皮与加筋肋几何参数分别见 表3和表4.

因满足全部相似条件极其困难，且完全相似在实际情况中也不适用，故可忽略完全相似的部分非 重要相似条件，进行结构的不完全相似研究.通过放松广义相似条件，开展缩尺模型的材料和几何尺寸 均发生变化的不完全相似研究.此时，假设模型的蒙 皮几何尺寸具有相同的几何缩尺因子，且模型与原型具有相同的边界条件，可得如下相似关系：

不完全相似缩尺模型的蒙皮几何参数的缩尺因 子均取10，同时，缩尺模型的蒙皮和加筋肋的材料分别使用铝（Al）、紫铜（Copper）、黄铜（Brass）和塑料（PVC），表5 列出了缩尺模型的材料参数.根据式（26）求得缩尺模型环向和纵向等效加筋肋的几何尺寸，发现它们的几何缩尺因子与蒙皮的几何缩尺因 子相等.

实际工程中的薄壳结构通常存在着一定的初始 几何缺陷.其中，酒窝缺陷与焊缝缺陷为典型且不利 缺陷.因此，引入不同幅值的酒窝缺陷与环向焊缝缺 陷，进行含初始缺陷的纵环离散加筋圆柱壳轴压后屈曲不完全相似分析.

3.1含酒窝缺陷纵环离散加筋圆柱壳轴压后屈曲不完全相似分析

采用式（23）建立含酒窝缺陷的纵环加筋圆柱壳 原型与缩尺模型.其中，缺陷幅值取 δ0=IF·t，IF代表初始几何缺陷的缺陷因子，在结构环向加筋肋上施 加2个酒窩缺陷，结构变形图如图3所示.

4 种不同模型材料的T 形纵环加筋圆柱壳轴压后屈曲不完全相似模拟的结果见图4～图7.由图可 知，在结构达到屈曲前，其荷载与位移处于近似线性关系;当荷载达到上临界点时，荷载随位移陡然下降，结构进入后屈曲阶段;同时，随着IF值的增大，结构上临界点对应的屈曲荷载逐渐减小.表6为预测原型与原型的上临界屈曲荷载的误差对比.由表6可知，随着模型与原型所取材料泊松比偏差的增大，预测原型与原型的上临界点屈曲荷载的偏差也逐渐 增大.IF=1，模型材料为Al时，T型纵环加筋圆柱壳平衡路径上临界点径向位移矢量和云图对比见图8.通过对比上临界点处屈曲模态图可知，上临界点处 缩尺模型与其对应原型的屈曲模态均相同.由以上分析可知，基于缩尺原理公式，缩尺模型能较好地预测其对应原型的平衡路径和屈曲模态.

3.2 含环向焊缝缺陷纵环离散加筋圆柱壳轴压后屈 曲不完全相似分析

采用式（24）建立含环向焊缝缺陷的纵环加筋圆 柱壳原型与缩尺模型，其中缺陷幅值取 δ0=IF·（t+bf+hw）.在结构每条环向加筋肋翼缘的两端上施加2条环向焊缝缺陷，结构变形图见图9.

4 种不同模型材料的T型纵环加筋圆柱壳轴压后屈曲不完全相似模拟的结果见图10～图13.由图可知，结构达到屈曲前，荷载与位移处于近似线性关系;当荷载达到上临界点时，荷载随位移陡然下降，结构进入后屈曲阶段;同时，随着IF值的增大，结构上临界点所对应的屈曲荷载逐渐减小.表7为预测原型与原型的上临界屈曲荷载的误差对比.由表7可知，随着模型与原型所取材料的泊松比偏差的增 大，预测原型与原型的上临界点屈曲荷载的偏差也 逐渐增大.IF=0.1，模型材料为Al时，T型纵环加筋圆 柱壳平衡路径上临界点径向位移矢量和云图对比见 图14.通过对比上临界点处屈曲模态图可知，上临界 点处缩尺模型与其对应原型的屈曲模态均相同.根据以上分析可知，基于缩尺原理公式，缩尺模型能较好地预测其对应原型的平衡路径和屈曲模态.

4 结论

本文以纵环离散加筋圆柱壳为研究对象，根据离散加筋理论和能量法推导出结构轴压后屈曲的广义相似条件与缩尺原理公式;结合轴压后屈曲缩尺 原理公式，对含初始缺陷纵环加筋圆柱壳的原型和缩尺模型，进行了结构轴压后屈曲的不完全相似分析.得到如下结论：

1）纵环离散加筋圆柱壳缩尺模型的轴压后屈 曲荷载位移曲线，结合结构轴压后屈曲不完全相似 缩尺原理公式，能较好预测原型结构轴压后屈曲的结果.随缩尺模型与原型的材料泊松比偏差的增大，由纵环离散加筋圆柱壳不完全相似缩尺模型预测的原型结构荷载位移曲线与原型结构结果的偏差逐渐 增大.因此，在利用纵环离散加筋圆柱壳轴压后屈曲不完全相似缩尺模型设计方法和缩尺原理公式进行相似预报时，模型结构与原型结构的材料泊松比应相近.

2）提出的纵环离散加筋圆柱壳轴压后屈曲的缩尺模型设计方法和缩尺原理公式适用于不同几何 缺陷形式和缺陷幅值的加筋圆柱壳轴压后屈曲相似 预报，并且能比较准确地预报大型加筋圆柱壳轴压后屈曲特性.这为采用离散加筋圆柱壳轴压后屈曲 缩尺模型实验预测其对应原型的后屈曲特性提供了参考.

参考文献

[1]于伟.新型干式煤气柜结构的非线性屈曲与稳定研究[D].重庆：重庆大学，2016：1-14.

YU W.Study on nonlinear buckling and stability of new typical dry gasholder[D].Chongqing：Chongqing University，2016：1-14.（In Chinese）

[2]杨金花，傅衣铭.具脱层复合材料层合圆柱壳的屈曲分析[J].湖南大学学报（自然科学版），2005，32（5）：25-30.

YANG J H，FU Ym.Buckling analysis of composite laminated cy-lindrical shell with delamination[J].Journal of Hunan University（Natural Sciences），2005，32（5）：25-30.（In Chinese）

[3] 向红，傅衣铭，鲁永红.具损伤正交各向异性板的后屈曲分析[J].湖南大学学报（自然科学版），2007，34（9）：57-61.   XIANG H，FU Ym，LU Y H.Post-buckling analysis of ortho-tropic plate considering damage[J].Journal of Hunan University（Natural Sciences），2007，34（9）：57-61.（In Chinese）

[4]SINGHATANADGID P， UNGBHAKORN V.Scaling laws forbuckling of polar orthotropic annular plates subjected to compres-sive and torsional loading[J].Thin-Walled Structures，2005，43（7）：1115-1129.

[5]HILBURGERmW，HAYNIE W T，LOVEJOY A E，et al.Sub-scale and full-scale testing of buckling-critical launch vehicle shell structures[C]// 53rd AIAA/ASME/ASCE/AHS/ASC Struc-tures，Structural Dynamics andmaterials Conference.Hawaii： American Institute of Aeronautics and Astronautics，2012：1688-1721.

[6]HILBURGERmW，LINDELLmC，WATERS W A，et al.Testand analysis of buckling-critical stiffenedmetallic launch vehicle cylinders[C]//2018 AIAA/ASCE/AHS/ASC Structures，Structural Dynamics，andmaterials Conference.Florida：American Institute of Aeronautics and Astronautics，2018：1697-1726.

[7]賈冬云，曹平周，姜德进.正多边形气柜立柱结构简化分析方法研究[J].工程力学，2010，27（6）：252-256.

JIA D Y，CAO P Z，JIANG D J.Study on simplified analyticalmethod for the column of regular polygon gasholder[J].Engineer-ingmechanics，2010，27（6）：252-256.（In Chinese）

[8]贾冬云，曹平周，姜德进，等.大型正多边形气柜壳体的试验研究[J].土木工程学报，2011，44（8）：52-58.

JIA D Y，CAO P Z，JIANG D J，et al.Experimental study of the shell of a large-scale regular polygon gasholder[J].China Civil Engineering Journal，2011，44（8）：52-58.（In Chinese）

[9]UNGBHAKORN V，SINGHATANADGID P.A scaling law for vi-bration response of laminated doubly curved shallow shells by en-ergy approach[J].mechanics of Advancedmaterials and Struc-tures，2009，16（5）：333-344.

[10]中国科学院力学研究所固体力学研究室板壳组.加筋圆柱曲板与圆柱壳[M].北京：科学出版社，1983：12-18.

Institute ofmechanics，Chinese Academy of Sciences，Group of Solidmechanics Research Shell.Stiffened cylindrical panels and cylindrical shells[M].Beijing：Science Press，1983：12-18.（In Chinese）

[11] AMABILIm.Nonlinear vibrations and stability of shells andplates[M].Cambridge ：Cambridge University Press，2008：29-32.

[12] FISHER C A.Dynamic buckling of an axially compressed cylindri-cal shell with discrete rings and stringers[D].Oklahoma：The Uni-versity of Oklahoma Graduate College，1972：66-70.

[13] 陈骥.钢结构稳定理论与设计[M].北京：科学出版社，2001：255-256

CHEN J.Stability of steel structures theory and design[M].Bei-jing：Science Press，2001：255-256.（In Chinese）

[14] COHEN-TANNOUDJI C，DIU B，LALOE F.Quantummechan-ics，Volume II[M].New York：Wiley，1977：1469-1471.

[15] WANG B，HAO P，LI G，et al.Determination of realistic worst im-perfection for cylindrical shells using surrogatemodel[J].Struc-tural &multidisciplinary Optimization，2013，48（4）：777-794.

[16] ROTTER Jm，TENG J G.Elastic stability of cylindrical shellswith weld depressions[J].Journal of Structural Engineering，1989，115（5）：1244-1263.