混合配筋偏心受压构件正截面承载力计算理论和方法

张望喜 胡彬彬 易伟建

摘 要：为完善钢筋和纤维增强复合材料（FRP）筋混合配筋混凝土偏心受压构件正截面 承载力计算方法，基于已有钢筋和玻璃纤维增强复合材料（GFRP）筋混合配筋混凝土偏压构件试验，通过试验现象和破坏形态归纳出三种典型的破坏类型，进而分析各破坏类型之间的界限，给出了相对界限受压区高度.利用ABAQUS进行参数分析，得到混合配筋混凝土偏压构件二阶弯矩增大系数表达式，考虑基本假定以及二阶效应的影响，推导了矩形截面偏压构件 正截面承载力计算公式.通过对比计算结果与试验结果，发现本文建议的计算公式具有很好的准确性和实用性（试验值与计算值之比Nu，t / Nu，e的均值为0.99，标准差为0.053），可为混合 配筋混凝土偏压构件在实际工程中的应用和推广提供一定的理论指导和设计借鉴.

关键词：混合配筋;偏压构件;正截面;承载能力;计算理论

中图分类号：TU375.4 文献标志码：A

Calculation Theory and Method of Normal Section Bearing Capacity of Eccentric Compression Member Reinforced with

Steel Bars and Fiber Reinforced Polymer Bars

ZHANG Wangxi1，2?，HU Binbin2，YI Weijian1，2

（1.Hunan Provincial Key Laboratory on Diagnosis for Engineering Structures（Hunan University），Changsha 410082，China;

2.College of Civil Engineering，Hunan University，Changsha 410082，China）

Abstract：To improve the calculation method of normal section bearing capacity of eccentric compression mem-ber reinforced with steel bars and Fiber Reinforced Polymer（FRP）bars，this study summed up three typical failure types，then analyzed the limit failures among each failure type，and gave relative-boundary compressive region′s height based on several tests of concrete members reinforced with steel bars and Glass Fiber Reinforced Polymer（GFRP）bars under eccentric compression.The second-order moment augmentation factor was obtained through pa-rameter analyses using ABAQUS.By considering the basic assumptions and the influence of the second-order bend-ing moment，the calculation formulas for the normal section bearing capacity of the rectangular section eccentric com-pression members were derived.By comparing the calculation results with the test results，it was proved that the cal-culation formulas proposed in this paper had good accuracy and practicability（the mean value of the ratio Nu，t/Nu，e between the experimental values and the calculated values was0.99and the standard deviation was0.053），whichcan provide a certain theoretical guidance and design reference for the application and promotion of concrete eccen-tric compression members reinforced with FRP bars and steel bars in practical engineering.

Key words：hybrid reinforcement;eccentric compression member;normal section;bearing capacity;calculation theory

钢筋混凝土結构耐久性问题引起了人们的广泛关注，钢筋锈蚀是造成钢筋混凝土结构过早失效的主要原因之一，各国每年花费大量的人力与物力用于结构加固或替换[1].目前，减少钢筋锈蚀的方法主 要有：增大混凝土的保护层厚度、提高混凝土的密实 性、在钢筋表面涂抹环氧树脂等[2-3]，虽然这些方法 延缓了钢筋的锈蚀，但难以从根本上解决混凝土结构耐久性问题.为此，必须找到一种耐腐蚀并且可以代替钢筋作用的材料.纤维增强复合材料（FRP）筋是一种抗拉强度高、密度小、耐腐蚀性好的筋材，并 且和混凝土有良好的共同工作性能[4]，因此可以替 代混凝土构件中的普通钢筋[5]，从而改善或解决由 钢筋锈蚀导致的混凝土结构耐久性问题.

目前，FRP筋已在实际工程中广泛应用，包括大跨度桥梁梁板、临时基坑支护、水工构筑物、特殊的军用建筑、医疗核磁共振设备等[6-7].由于FRP 筋具有较低的弹性模量、线弹性的本构关系[8-9]，配置 FRP 筋的混凝土构件可能会发生脆性破坏，在正常 使用状态下也可能会产生过大的裂缝宽度和挠度.在矩形截面的混凝土构件中，边角区钢筋由于双向侵蚀和应力共同作用，导致较早出现锈蚀，因此可以将 FRP 筋布置在截面易发生腐蚀的边角区域，将普 通钢筋布置在截面内部，这样不仅改善了钢筋混凝 土结构耐久性问题，也解决了FRP 筋混凝土结构脆 性破坏的问题[10-11].

很多学者进行了FRP筋混凝土受压构件的试验研究，并发现 FRP 筋与混凝土具有良好的共同工作 性能[12-14]，我国规范[15-16]也涉及到了FRP 筋受压构件的设计计算.当钢筋和FRP 筋混合配筋用在混凝 土偏压构件中时，由于FRP 筋和钢筋物理性能以及力学性能不同，已有规范的承载力计算公式不再适用于钢筋和FRP筋混合配置的混凝土偏压构件承载力计算.本文基于若干假定，以玻璃纤维增强复合材 料（GFRP）筋为例，推导出钢筋和GFRP 筋混合配筋 混凝土偏压构件的承载力计算公式，为实际工程计算提供安全可靠的依据.

1混合配筋混凝土偏压构件破坏特征

1.1破坏类型

根据试验现象和结果[4，17-24]，偏心荷载作用下混 合配筋混凝土柱的破坏类型可归结为三种：屈服-受拉破坏、屈服-受压破坏和受压破坏.

1.1.1屈服-受拉破坏

当轴向力N的偏心距较大，且纵向钢筋的配筋率不高时，在N 作用下截面呈现出部分受压、部分受拉的特点.随着荷载的增加，混凝土受拉侧很快出现 横向裂缝，由于纵筋配筋率不高，受拉纵筋的应力增长较快，钢筋先屈服，钢筋塑性伸长导致裂缝向受压区急剧扩展，而后 GFRP筋被拉断.在这种破坏形式下，受拉钢筋先屈服，实现了刚度的转折，表现出一定的延性破坏的特征.

1.1.2 屈服-受压破坏

这类破坏形式，和屈服-受拉破坏相似.不同之处在于，钢筋屈服后，GFRP 筋在受压区混凝土达到极限压应变之前没有被拉断.此时该破坏模式具有明显的预兆，横向裂缝快速扩展，变形显著增大，具有塑性破坏的特点.

1.1.3受压破坏

当轴向力N的偏心距较小，或偏心距较大且纵向钢筋的配筋率很高时，在N 作用下截面可能呈现 出部分受压、部分受拉或全截面受压的状态.远离轴力一側的钢筋未发生屈服，GFRP 筋未破坏，靠近轴力一侧的混凝土达到极限压应变.这类破坏发生时，没有明显的预兆，具有脆性破坏的特点，在设计时应该避免此类破坏的发生.

1.2 界限破坏

从上述破坏类型可以看出，屈服-受拉破坏与屈 服-受压破坏的区别就在于GFRP筋是否被拉断，屈 服-受压破坏与受压破坏的区别就在于钢筋是否屈 服.若钢筋屈服且构件以GFRP筋被拉断而破坏，则是屈服-受拉破坏;若钢筋屈服且构件以混凝土被压碎而破坏，则是屈服-受压破坏;若钢筋未屈服且构件以混凝土被压碎而破坏，则是受压破坏.

图1所示为混合配筋混凝土偏心受压构件的截 面应变，图中εs为远离轴力一侧的纵筋拉应变，εfu为GFRP 筋极限拉应变，εy为钢筋屈服时对应的拉应变，εcu为混凝土的极限压应变.当εs> εfu时，钢筋屈 服，GFRP 筋被拉断，截面为屈服-受拉破坏（如图1中的ab）;当εs=εfu时，GFRP 筋被拉断的同时，受压区边缘混凝土达到极限压应变，为屈服-受拉破坏与屈 服-受压破坏的界限（如图1中的ac）;当εy<εs<εfu时，钢筋屈服，GFRP 筋未被拉断，混凝土被压碎，截面为屈服-受压破坏（如图1中的ad）;当εy=εs<εfu时，为屈 服-受压破坏与受压破坏的界限（如图1中的ae）;当εs<εy时，钢筋未屈服，截面为受压破坏（如图1中的af）;当到达g点时，进入全截面受压状态.由此可以计算出屈服-受拉破坏与屈服-受压破坏的相对界限受压区高度ξb1以及屈服-受压破坏与受压破坏的相对界限受压区高度ξb2.当ξ≤ξb1时，为屈服-受拉破 坏;当ξb1<ξ≤ξb2时，为屈服-受压破坏;当ξ>ξb2时，为受压破坏.

式中：xb1、xb2以及x0b1、x0b2分别为按等效矩形应力图形以及平截面假定计算的受压区高度;h0为截面有效高度;β1为和等效矩形应力图形有关的参数;ffu为GFRP 筋极限抗拉强度;fy为钢筋屈服强度;Ef和Es分别为GFRP 筋和钢筋的受拉弹性模量.

2  偏压构件正截面承载力计算

2.1 基本假定

本文的公式推导基于以下假定：1）截面应变符 合平截面假定[25];2）不考虑受拉区混凝土的抗拉强度;3）钢筋和GFRP 筋与混凝土有良好的黏结作用，在截面同一位置处，钢筋与GFRP 筋应变相同;4）混 凝土受压的应力-应变曲线，按 GB 50010—2010[26]中的规定采用，见图2（a）;5）钢筋和GFRP 筋受拉的应力-应变曲线见图2（b）和（c）;6）纵筋的应力为纵筋的应变乘以相应的弹性模量，但不超过其抗拉强度与抗压强度.

GFRP 筋线弹性的本构关系，导致其发生脆性破 坏，为了使 GFRP 筋在使用时具有一定的安全储备度，取其抗拉强度设计值[16，26-27]为：

式中：ffy、ffk分别为GFRP 筋的抗拉强度设计值、标准 值;γf为GFRP 筋的材 料分项系数，取1.25;γe 为GFRP 筋的环境影响系数，室内环境取1.25，一般室 外环境取1.4，海洋环境、侵蚀性环境取1.6（强碱环 境取 2.0）;CE为GFRP 筋环境折减系数，非侵蚀环境取0.8，侵蚀环境取0.7.

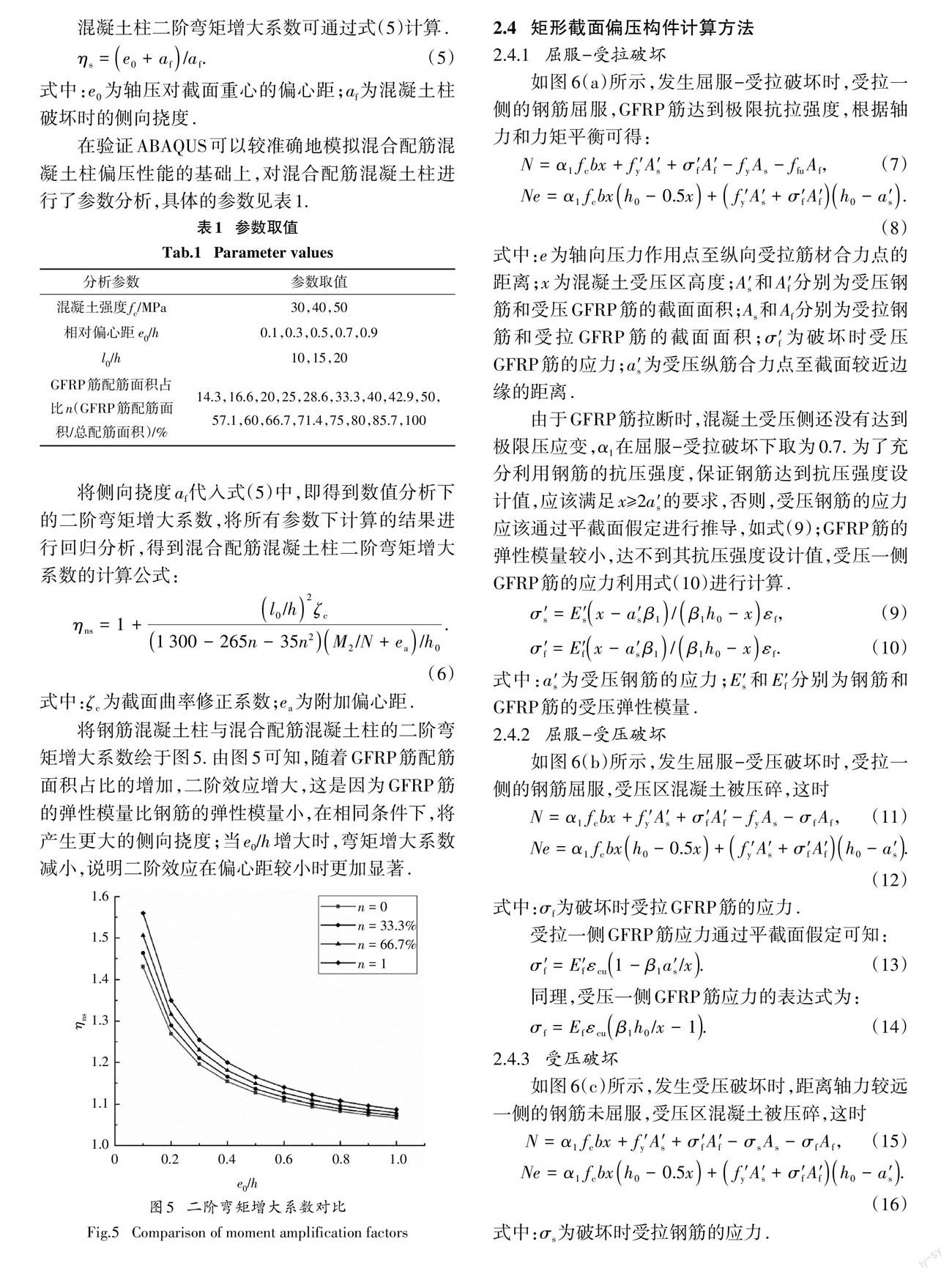
在混合配筋混凝土柱中，当GFRP 筋达到设计应力时，由平截面假定可知，钢筋应力σs=Esffy/Ef，若钢筋未屈服，则 σs=Esffy/Ef

2.2 混合配筋配置形式

关于混合配筋的配置形式，部分学者更加倾向于在单层配筋中用GFRP 筋代替部分钢筋，但为了更好地解决由钢筋锈蚀导致的混凝土耐久性问题，也有对双层混合配筋混凝土柱的研究，在外侧配置 GFRP 筋，在内侧配置钢筋.此时，钢筋与GFRP 筋的有效高度h0=h-c-ds-d-4s/5，其中h为截面高度，c为保护层厚度，ds为箍筋直径，d为外侧 GFRP 筋直径，s为两排配筋之间的距离，通过这种方法计算的有效高度，具有更高的安全系数，下面证明这种计算方法的可行性.图3为双层混合配筋示意图，h01、h02为钢筋、GFRP 筋合力作用点到截面受拉受压分界点的距离.

钢筋和GFRP筋分别对分界点的弯矩的和为Mh=σsAsh01+ σfAfh02，钢筋和GFRP筋合力作用点对分界 点的弯矩为Mh0=（σsAs+σfAf）（4h01/5+h02/5）.由平截面 假定可知，εf=εsh02/h01，假设钢筋的弹性模量是 GFRP 筋的4倍，一排和二排配筋面积相等，则有Mh-Mh0=（EsεsAfh02/5h01-EsεsAs/5）（h02-h01）>0，说明利用上述公式计算的有效高度是偏于安全的.

2.3 P-6 二阶效应

当偏心受压构件的长细比以及轴压比偏大，反 弯点不在杆件高度范围内时，经P-δ效应放大后，弯 矩控制截面可能会从构件端部转移到构件中部.因 此，在截面设计时应考虑 P-δ效应的不利影响.

2.3.1  长细比限值

我国规范GB 50010—2010[26]和美国规范ACI318—19[28]中对需要考虑钢筋混凝土柱 P-δ效应的情况进行了规定，即单曲率对称弯曲的钢筋混凝土 柱的长细比大于22.但由于GFRP 筋的弹性模量低于钢筋，文献[29]建议单曲率对称弯曲的FRP 筋混 凝土柱长细比限值取17.为了充分考虑附加挠度对构件产生的影响，钢筋和GFRP 筋混合配筋混凝土柱 长细比限值也取17.当混合配筋混凝土柱长细比满 足式（4）时，不需要考虑 P-δ效应[30].

式中：l0为构件计算长度;i为回转半径;M1、M2分别为已经考虑侧向挠度的偏心受压构件两端截面按弹 性分析确定的对同一主轴的组合弯矩设计值，绝对值较小的杆端弯矩为M1，绝对值较大的杆端弯矩为M2，当构件单曲率弯曲时，M1和M2 均取正值，否则取负值.

2.3.2 二阶弯矩增大系数

由于GFRP 筋和钢筋力学性能的差异，很难通过理论推导得出正确的弯矩增大系数[31].因此，本文将 基于ABAQUS有限元软件进行参数分析拟合出混合 配筋混凝土柱二阶弯矩增大系数.

为验证利用ABAQUS有限元软件进行数值分析的正确性，建立了46个模型[4，18-24]，将由模拟得出的偏压柱峰值荷载和峰值荷载下对应的侧向挠度和试 验结果进行对比，结果见图4.Nt/Ns表示试验峰值荷 载和模拟峰值荷载的比值，δt/δs表示试验侧向挠度和模拟侧向挠度的比值，Nt/Ns的平均值为0.955，标准 差为0.004，δt/δs的平均值为0.986，标准差为0.029.由 此可见，ABAQUS可以较好地模拟混合配筋混凝土 柱的承载力和侧向挠度.

式中：e0为轴压对截面重心的偏心距;af为混凝土柱 破坏时的侧向挠度.

在验证ABAQUS可以较准确地模拟混合配筋混 凝土柱偏压性能的基础上，对混合配筋混凝土柱进行了参数分析，具体的参数见表1.

将侧向挠度af 代入式（5）中，即得到数值分析下的二阶弯矩增大系数，将所有参数下计算的结果进行回归分析，得到混合配筋混凝土柱二阶弯矩增大系数的计算公式：

将钢筋混凝土柱与混合配筋混凝土柱的二阶弯 矩增大系数绘于图5.由图5可知，随着 GFRP 筋配筋 面积占比的增加，二阶效应增大，這是因为GFRP 筋的弹性模量比钢筋的弹性模量小，在相同条件下，将 产生更大的侧向挠度;当e0/h增大时，弯矩增大系数减小，说明二阶效应在偏心距较小时更加显著.

2.4 矩形截面偏压构件计算方法

2.4.1  屈服-受拉破坏

如图6（a）所示，发生屈服-受拉破坏时，受拉一侧的钢筋屈服，GFRP 筋达到极限抗拉强度，根据轴力和力矩平衡可得：

式中：e为轴向压力作用点至纵向受拉筋材合力点的距离;x为混凝土受压区高度;A和Af′分别为受压钢 筋和受压 GFRP 筋的截面面积;As和Af分别为受拉钢 筋和受拉 GFRP 筋的截 面 面 积;σf′为破 坏时受压 GFRP 筋的应力;a为受压纵筋合力点至截面较近边 缘的距离.

由于GFRP 筋拉断时，混凝土受压侧还没有达到极限压应变，α1在屈服-受拉破坏下取为0.7.为了充分利用钢筋的抗压强度，保证钢筋达到抗压强度设计值，应该满足 x≥2a的要求，否则，受压钢筋的应力应该通过平截面假定进行推导，如式（9）;GFRP 筋的弹性模量较小，达不到其抗压强度设计值，受压一侧GFRP筋的应力利用式（10）进行计算.

2.4.2 屈服-受压破坏

如图6（b）所示，发生屈服-受压破坏时，受拉一侧的钢筋屈服，受压区混凝土被压碎，这时

2）在进行混合配筋偏压构件屈服-受拉破坏以及GFRP 筋混凝土偏压构件受拉破坏正截面承载力计算时，GFRP 筋使用的是极限抗拉强度，但 GFRP 筋应力-应变关系呈线性，没有明显的屈服点，因此为了增加构件的安全储备，建议在进行截面设计时，使用GFRP 筋抗拉强度设计值，计算公式和上述相似，不再赘述.

2.5 -相关曲线

根据轴力和弯矩平衡方程，可以得到轴力和弯 矩之间的相关关系，现以实例说明.混凝土柱的截面 尺寸 b×h为340mm×340mm，混凝土保护层厚度c= 25mm，fc=31.1MPa，fy=fy′=400mPa，ffu=840mPa，ff=840mPa，混凝土柱采用对称配筋，单侧配筋形式为： 柱 Ⅰ 选用7?12，柱 Ⅱ 选用4?12+312，柱 Ⅲ 选用2?12+512，柱Ⅳ选用712，?表示 GFRP 筋，表示 钢 筋.设= N/fc bh0，= M/fc bh，将 柱 Ⅰ ～ 柱 Ⅳ的-相关曲线绘于图7.

以柱Ⅱ为例，说明混合配筋混凝土柱-相关曲线的特点.屈服-受拉破坏和屈服-受压破坏只是 GFRP 筋应力不同，没有明显的分界点，以ab 段表示，截面承受的弯矩 M随着轴力N的增大而增大，b 点为屈服-受压破坏和受压破坏的界限状态，在此点弯矩值最大，bc 段表示受压破坏时的N-M曲线，截面 承受的弯矩 M随着轴力N的增大而减小.a 点轴向力为0，表示构件处于受弯状态，c 点弯矩为0，表示构件处于轴心受压状态.从图7中可以看出，柱Ⅳ的-相关曲线位于最外侧，说明钢筋混凝土柱的承载力最高，随着 GFRP 筋配筋面积的增加，混凝土 柱的承载能力逐渐降低，但其界限破坏点逐渐升高，延性增加，这和Elchalakani等[4]的研究结果相同.

3公式准确性对比验证

选取已有文献中的试验试件，根据试件不同的破坏特征代入不同的方程组进行求解，将理论承载力值与试验承载力值进行对比，详见表2.结果表明，理论公式计算值与试验实测值相差不大（试验值与计算值之比Nu，t/Nu，e的均值为0.99，标准差为0.053），说明计算公式具有较好的准确性，可以用来指导工 程设计计算.

4结论

1）钢筋和GFRP 筋混合配筋偏心受压构件有屈 服-受拉破坏、屈服-受压破坏以及受压破坏三种破 坏模式.

2）当混合配筋混凝土偏压构件的长细比大于17时，可依据本文推导的考虑 GFRP筋配筋面积占比的二阶弯矩增大系数考虑侧向挠度对构件承载力的不 利影响.

3）基于若干假定推导出的矩形截面偏心受压构件承载力计算公式具有良好的准确性和适用性，可为混合配筋混凝土构件在实际工程中的应用和推广 提供一定的理论指导和设计借鉴.

参考文献

[1]HASAN H A，SHEIKH M N，HADI M N S.Maximum axial load

carrying capacity of Fibre Reinforced-Polymer（FRP） bar rein-forced concrete columns under axial compression[J].Structures，2019，19：227-233.

[2]叶列平，冯鹏.FRP在工程结构中的应用与发展[J].土木工程学报，2006，39（3）：24-36.

YE L P，FENG P.Applications and development of fiber-reinforced polymer in engineering structures[J].China Civil Engi-neering Journal，2006，39（3）：24-36.（In Chinese）

[3]谭永山，余红发，梅其泉，等.不同措施对热带海洋砼结构服役寿命的影响[J].湖南大学学报（自然科学版），2018，45（6）：97-105.

TAN Y S，YU H F，MEI Q Q，et al.Effects of various measures on service life of concrete structure in tropical marine environment[J].Journal of Hunan University（Natural Sciences），2018，45（6）：97-105.（In Chinese）

[4]ELCHALAKANI M，MA G W.Tests of glass fibre reinforced poly-mer rectangular concrete columns subjected to concentric and ec-centric axial loading [J].Engineering Structures，2017，151：93-104.

[5]董志強，吴刚.FRP 筋增强混凝土结构耐久性能研究进展[J].土木工程学报，2019，52（10）：1-19.

DONG Z Q，WU G.Research progress on durability of FRP bars reinforced concrete structures [J].China Civil Engineering Jour-nal，2019，52（10）：1-19.（In Chinese）

[6]代力.持续荷载与环境作用下混凝土梁中GFRP筋抗拉性能研究[D].武汉：武汉理工大学，2017：9-11.

DAI L.Study on tensile properties of GFRP bars embedded in con-crete beams under sustained load and environmental effects[D].Wuhan：Wuhan University of Technology，2017：9-11.（In Chi-nese）

[7]OMER A I I.Experimental and theoretical study on seismic behav-

ior of concrete columns reinforced with steel-basalt FRP compos-ite bars and hybrid stirrups [D].Nanjing：Southeast University，2016：1-2.

[8]葉列平，冯鹏，林旭川，等.配置 FRP的结构构件的安全储备指标及分析[J].土木工程学报，2009，42（9）：21-31.

YE L P，FENG P，LIN X C，et al.Analysis of safety margin indi-ces for structural members with FRP[J].China Civil Engineering Journal，2009，42（9）：21-31.（In Chinese）

[9]朱德举，徐旭锋，郭帅成，等.高温后玄武岩和玻璃纤维增强复合材料筋的力学性能[J].湖南大学学报（自然科学版），2021，48（7）：151-159.

ZHU D J，XU X F，GUO S C，et al.Mechanical properties of basalt and glass fiber reinforced polymer tendons after exposed to el-evated temperatures[J].Journal of Hunan University（Natural Sci-ences），2021，48（7）：151-159.（In Chinese）

[10]庞蕾，屈文俊，李昂.混合配筋混凝土梁抗弯计算理论[J].中国公路学报，2016，29（7）：81-88.

PANG L，QU W J，LI A.Calculation of flexural strength for con-crete beams reinforced with hybrid（FRP and steel）bars[J].China Journal of Highway and Transport，2016，29（7）：81-88.（In Chi-nese）

[11]SUN Z Y，WU G，ZHANG J，et al.Experimental study on concrete

columns reinforced by hybrid steel-fiber reinforced polymer（FRP）bars under horizontal cyclic loading[J].Construction and Building Materials，2017，130：202-211.

[12]KHARAL Z，SHEIKH S A.Seismic behavior of square and circu-lar concrete columns with GFRP reinforcement [J].Journal of Composites for Construction，2020，24（1）：04019059.

[13]GURI Z，MISINI M.Experimental and numerical study of circular

columns reinforced with steel and glass FRP bars[J].Magazine of Concrete Research，2021，73（4）：163-173.

[14]SUN L，YANG Z Y，JIN Q，et al.Effect of axial compression ratio

on seismic behavior of GFRP reinforced concrete columns[J].In-ternational Journal of Structural Stability and Dynamics，2020，20（6）：2040004.

[15]纤维增强复合材料筋混凝土桥梁技术标准：CJJ/T 280—2018[S].北京：中国建筑工业出版社，2018：21-24.

Technical standard for concrete bridge with FRP reinforcements： CJJ/T 280—2018 [S].Beijing ：China Architecture & Building Press，2018：21-24.（In Chinese）

[16]纤维增强复合材料工程应用技术标准：GB 50608—2020[S].北京：中国计划出版社，2020：21，104-108.

Technical standard for fiber reinforced polymer（FRP）in constru-tion：GB 50608—2020[S].Beijing：China Planning Press，2020： 21，104-108.（In Chinese）

[17]ISSA M，METWALLY I，ELZEINY S.Performance of eccentri-cally loaded GFRP reinforced concrete columns[J].World Journal of Engineering，2012，9（1）：71-78.

[18]SUN L，WEI M H，ZHANG N.Experimental study on the behav-ior of GFRP reinforced concrete columns under eccentric axial load

[J].Construction and Building Materials，2017，152：214-225.[19]刘景.GFRP 筋混凝土柱偏压破坏机理及设计方法研究[D].武汉：武汉理工大学，2017：44-63.

LIU J.Failure mechanism and calculation methods studies on ec-centric loaded concrete columns reinforced with GFRP bars[D].Wuhan：Wuhan University of Technology，2017：44-63.（In Chi-nese）

[20]林澤昕.偏压荷载作用下GFRP 筋混凝土柱试验研究和纵筋配筋率计算[D].武汉：武汉理工大学，2018：32-33.

LIN Z X.Experiment of reinforced concrete columns with GFRP bars under eccentric axial compression load and longitudinal rein-forcement calculation[D].Wuhan：Wuhan University of Technol-ogy，2018：32-33.（In Chinese）

[21]汪光波.GFRP筋增强混凝土柱的抗压性能试验研究[D].武汉：武汉科技大学，2018：61-62.

WANG G B.Experimental study on compressive performance of concrete columns reinforced by GFRP bars[D].Wuhan：Wuhan University of Science and Technology，2018：61-62.（In Chinese）

[22]高伟男.碱、盐环境下FRP 筋抗压强度耐久性及FRP 筋与钢筋混杂配筋混凝土柱偏压试验研究[D].北京：北京工业大学，2017：54-67.

GAO W N.Experimental study on compressive strength of FRP rebars in alkali and salt solution and eccentric compression of con-crete column with hybrid reinforcement of FRP and steel rebars[D].Beijing：Beijing University of Technology，2017：54-67.（In Chinese）

[23]KHORRAMIAN K，SADEGHIAN P.Experimental and analytical

behavior of short concrete columns reinforced with GFRP bars un-der eccentric loading [J].Engineering Structures，2017，151：761-773.

[24]KHORRAMIAN K，SADEGHIAN P.Experimental investigationof short and slender rectangular concrete columns reinforced withGFRP bars under eccentric axial loads[J].Journal of Composites for Construction，2020，24（6）：04020072.

[25]王国强，孙理想.GFRP 筋混凝土板正截面抗弯承载力研究[J].玻璃钢/复合材料，2017（7）：29-34.

WANG G Q，SUN L X.Research on the flexural behavior of con-crete slabs with hybrid reinforcement of gfrp bars[J].Fiber Rein-forced Plastics/Composites，2017（7）：29-34.（In Chinese）

[26]混凝土结构设计规范：GB 50010—2010[S].北京：中国建筑工业出版社，2011：34-35.

Code for design of concrete structures：GB 50010—2010[S].Beijing：China Architecture & Building Press，2011：34-35.（In Chinese）

[27]NANNI A.Guide for the design and construction of concrete rein-forced with FRP bars（ACI 440.1R-03）[C]//Structures Congress 2005.Reston，VA：American Society of Civil Engineers，2005：16-17.

[28]Building code requirements for structural concrete and commen-tary ：ACI318—19[S].Farmington Hills，MI：American Con-crete Institute，2019：67-68.

[29]MIRMIRAN A，YUAN W，CHEN X B.Design for slenderness inconcrete columns internally reinforced with fiber-reinforced poly-mer bars[J].ACI Structural Journal，2001，98：116-125.

[30]彭飞，薛伟辰.FRP 筋混凝土偏压柱承载力计算方法[J].建筑结构学报，2018，39（10）：147-155.

PENG F，XUE W C.Calculation approach of ultimate capacity of FRP reinforced concrete columns under eccentric compression[J].Journal of Building Structures，2018，39（10）：147-155.（In Chinese）

[31]许晶，贡金鑫 .无侧移钢筋混凝土柱荷载-变形特性及非线性二阶效应[J].建筑结构学报，2012，33（5）：93-104.

XU J，GONG J X.Load-deflection characteristic and calculation of second-order effect of non-sway reinforced concrete columns[J].Journal of Building Structures，2012，33（5）：93-104.（In Chinese）