考虑非平稳横风作用的列车-大跨斜拉桥耦合系统动力响应

何旭辉 谭凌飞 顾建华 敬海泉 李书昌

摘 要：為了研究非平稳横风对列车-大跨斜拉桥耦合系统的动力响应，首先使用EMD（经验模态分解）方法对已有实测台风数据进行处理，获得台风的时变平均风速，将风谱中的平均风速替换成时变平均风速，通过谐波合成法模拟得到非平稳横风脉动风速.使用有限元 软件 ANSYS和多体动力学软件 SIMPACK 建立列车-轨道-斜拉桥耦合分析模型，非平稳风荷 载包括时变平均风引起的静风力和非平稳脉动风引起的抖振力.计算了风-列车-大跨斜拉桥 耦合系统的动力响应，对比分析了平稳风与非平稳风作用下列车和斜拉桥的加速度响应以及桥上列车的安全舒适性指标.结果表明：对比平稳风，在非平稳风作用下列车的横向和竖向最大加速度分别增大了12%和23%，桥梁的横向和竖向最大加速度分别增大了16%和7%，列车的轮重减载率、轮轨横向力、脱轨系数分别增大了9%、14%和4%，列车的横向Sperling 指标有一定的增大，从而降低了桥上行车的安全性和舒适性;频谱图显示在低频区域内，非平稳风作用下列车的竖向振动、横向振动和桥梁的横向振动会更加强烈.

关键词：非平稳横风;风-车-桥;多体动力学;大跨斜拉桥;动力响应

中图分类号：U442 文献标志码：A

Dynamic Response of Train-Long Span Cable-stayed   Bridge Coupling System Considering Nonstationary Crosswind

HE Xuhui1，2，TAN Lingfei1，2，GU Jianhua3，JING Haiquan1，2?，LI Shuchang3

（1.School of Civil Engineering，Central South University，Changsha 410075，China;

2.National Engineering Laboratory for High-Speed Railway Construction Technology，Changsha 410075，China;

3.Guangdong Guangzhu Intercity Rail Transit Co，Ltd，Guangzhou 510335，China）

Abstract：In order to study the dynamic response of a non-stationary crosswind on the train-long span cable-stayed bridge coupling system，the EMD（Empirical Mode Decomposition）method is used to process the existing measured typhoon data to obtain the time-varying average wind speed of the typhoon.The average wind speed in the wind spectrum is replaced by the time-varying average wind speed，and the non-stationary crosswind fluctuating windspeed is simulated by the weighted amplitude wave superposition method.The finite element software ANSYSand the multi-body dynamics software SIMPACK are used to establish a train-track-cable-stayed bridge coupling analysis model.The non-stationary wind load includes the static wind caused by the time-varying average wind and the buffeting force caused by the non-stationary fluctuating wind.The dynamic response of the coupled system of wind-train-long-span cable-stayed bridge is calculated，and the acceleration responses of the train and cable-stayed bridge under the action of stationary wind and non-stationary wind as well as the safety and comfort indexes of the train on the bridge are compared and analyzed.The results show that compared with the stationary wind，the maximum lateral and vertical acceleration of the train are increased by12 % and 23% under the action of non-stationary wind，respectively，and the maximum lateral and vertical acceleration of the bridge are increased by16 % and 7 %，respectively.The wheel load reduction rate，wheel-rail lateral force and derailment coefficient of the train increase by9%，14 % and 4 %，respectively.The lateral Sperling index of the train increases to a certain extent，thus reducing the safety and comfort of driving on the bridge.The spectrum shows that in the low frequency region，the vertical vibration，transverse vibration of the train and the transverse vibration of the bridge are more intense un-der the action of non-stationary wind.

Key words：non-stationary crosswind;wind-vehicle-bridge;multibody dynamics;long-span cable-stayed bridge;dynamic response

截至2020年底，我国高铁运营里程达3.79万 km，成为世界上高速铁路里程最长、列车密度最高、网络结构最复杂的国家.众所周知，高速铁路有着高平顺性、高舒适性、高稳定性和高安全性的要求，现 代大跨度斜拉桥正朝着更大跨、更轻柔、更纤细的方向发展，因此当较大的铁路荷载作用在柔性的大跨斜拉桥上时，列车的行车安全性、舒适性和桥梁的安全性成为当下的热点问题[1].此外由于长三角、珠三角地区处在太平洋台风的直接侵袭范围，与常规的风相比，台风的风速更大，非平稳特性更显著，因此 台风的到来会对高速列车安全产生更不利的影响，高速列车的行车安全性将遭遇更大的挑战.

国内外学者已经对风-车-桥系统耦合振动开展了大量研究[2]，夏禾等[3]提出了一种基于Monte Carlo 技术模拟随机风速场下列车-桥梁系统动力可靠性的分析方法.郭向荣等[4]考虑脉动风沿桥梁纵向的空间相关性，随机模拟出沿桥跨若干点处的风速时程曲线，采用时域分析法对脉动风作用下高速列车 通过该桥时的车桥时变系统动力响应进行较详细的分析，从安全性与舒适性两方面计算分析该桥列车行车的临界风速.李永乐等[5-6]利用自制的气动力分离装置-交叉滑槽系统在风洞试验中研究了车辆和桥梁之间的气动影响，使用自编程技术建立了风-车-桥非线性空间耦合振动分析模型.韩艳等[7]研究 车桥间气动干擾对桥上车辆行驶的影响，研究结果表明：考虑车桥间气动干扰对车辆动力响应影响较大.Montenegro等[8]使用欧洲标准化委员会（CEN）离 散阵风模型和基于随机生成风场的湍流风模型模拟 生成了两种不同风模型，研究了不同风模型对列车 侧风稳定性的影响.

上述风-车-桥系统耦合振动的研究多将风视为平稳随机过程，因此没有对非平稳风作用下的列车-桥梁振动进行研究.由于缺乏理论分析框架，对风-车-桥非平稳耦合振动的研究报道相当少见.然而，大多数列车倾覆事故实际上是由于重要的非平稳因 素相关的极端风造成的[9].与静止边界层风相比，非 平稳极端风的风速呈现出时变均值、时变方差、时变频率等时变特征[10-11].此外，在相对较短的持续时间 内，这些极端事件中的风速可以达到平均值的数倍[12].何旭辉等[13]基于伪激振法（PEM），建立了非平 稳风作用下高速列车-桥梁耦合振动的有效分析框 架，证明了风的非平稳特性对列车-桥梁耦合作用系统的动力性能有重要影响，其不足之处在于没有考 虑真实的轮轨关系.因此，研究非平稳特性对车桥系统振动的影响具有重要意义.

本文的研究背景是在建的金海特大桥，该桥是 主跨为3×340m的四塔斜拉桥，也是世界上首座公路 铁路两用的四塔斜拉桥，桥址靠近南海，所处的风环 境十分恶劣，常年遭受台风侵袭，因此，开展非平稳 风作用下大跨度斜拉桥桥上行车安全研究是十分有必要的.本文通过EMD（Empirical Mode Decomposi-tion）方法从已有的实测台风数据中提取出时变平均风速，将风谱中的平均风速替换成时变平均风速，通 过谐波合成法模拟得到非平稳风脉动风速，将列车和桥梁的风荷载时程施加到由有限元分析软件 ANSYS和多体动力学软件 SIMPACK联合建立的风-高速列 车-大跨斜拉桥耦合分析模型当中，计算分析了平稳 风与非平稳风作用下车桥系统的动力响应区别.

1非平稳风场模拟方法

1.1非平稳风速模型

在平稳风速模型研究中，在某一时刻 t的风速等于平均风速加上均值为零的平稳脉动风速，即

实测台风结果表明：不同于平稳边界层风速，台 风风速时常在均值、方差、频率等方面表现出明显的时变特征.目前国内外学者提出了一些非平稳模型 来描述台风和极端风的非平稳性，并与对台风或其 他极端风的非平稳风速认识基本保持一致，即非平

稳风速等于时变平均风速加上脉动风速，可表示为：

1.2 非平稳风场模拟

在进行风场模拟时，十分关键的一步就是对平 均风剖面模型的研究.根据已有研究结果，针对地表粗糙度较小的状况，本文中选用拟合效果较好的指数函数模型来描述台风平均风速随高度的变化规 律.指数函数风剖面经验模型见式（3）.

根据公式（2）可知，模拟非平稳风速需要分时变平均风速模拟和脉动风速模拟，然后再将这两部分叠加即可得到模拟出来的非平稳风速，图1所示为模拟流程图.

现有研究中，一般采用三种方法来获取时变平 均风速，分别是：①假定时变平均风速服从已知函数，如余弦函数;②从实际台风风速时程曲线中提 取;③假定时变平均风速为一常数.因为台风的非平 稳特性十分明显，风速变化很快，不同台风之间的物理特性相差较大，风速分布规律差别也较大，所以选用某一常数或服从某确定函数曲线的假定来模拟时变平均风速是不恰当的，因此本文使用EMD分解方法从实测的台风风速时程曲线提取时变平均风速，这样可信度高且准确度也高.

平稳风的脉动风速通常基于经典功率谱，使用谐波合成法进行模拟.由于台风风速的非平稳性明显，风速变化快，其平均速度也表现出较明显的时变性，而传统谐波合成法的平均风速为常量，基于进化谱的理念，在模拟台风脉动风速时，通过时变平均风速的变化来实现更新功率谱，从而实现对台风的模拟[14].将台风风场模拟时长 T分成N个足够小的时间间隔 ?t，T= N?t，在足够小的时间间隔 ?t 内任意时刻的风速可视为该?t 内的平均风速，也就是时变平均风速等于平均风速.因此在模拟台风时需要分两步：①在每个足够短的时间间隔 ?t 内，采用谐波合成法模拟零均值稳态脉动风速，实现每个足够短的时间间隔 ?t 内的脉动风模拟;②在不同时间间隔中，随着时变平均风速变化更新风功率谱，实现不同时间间隔内的脉动风速模拟.

1.2.1时间间隔 ?t 内的脉动风速模拟

直接采用谐波合成法对足够小的时间间隔 ?t 内的脉动风速进行模拟，以高度为z处的节 点 i（i=1，2，…，m）进行说明，具体步骤如下.

在模拟台风风场时，已有研究中，在水平顺风向一般选用经典风谱中的Kaimal谱作为功率谱密度函数，表达式如式（4）所示.

1.2.2 不同时间间隔内的脉动风速模拟

接着只需将式（4）中的功率谱更新，再重复第一步，就能获得每个时间间隔内的脉动风速.最后将脉动风速与时变平均风速相加就可获得非平稳风速.

2  风-列车-大跨斜拉桥耦合系统

2.1  作用在列车和桥梁上的非平稳风荷载

由数值模拟方法得到非平稳风场后，作用在列 车和桥梁上的风荷载分为两部分：一是由时变平均 风引起的时变静风荷载;二是由脉动风引起的非平 稳抖振力.由 Davenport 准定常理论可得，主梁和列车在时变平均风作用下的非平稳静风荷载可表示为：

式中：F（t）、F（t）、F（t）分别为由时变平均风产生的阻力、升力和力矩;ρ是空气密度;（t）为时变平均 风速;B为桥梁断面宽度;H为垂直于平均风向的侧 风投影面积（单位长度）;CD、CL和CM分别为阻力系数、升力系数和力矩系数.桥梁主梁和列车的三分力系数均通过风洞试验得到，0°风攻角时车-桥系统中列车与桥梁空气动力学参数见表1.

抖振力载荷是由随机风的脉动量引起的.根据 准定常假定，主梁的抖振力载荷根据公式（8）计算.

式中：F（t）、F（t）、F（t）分別为抖振阻力、抖振升力和抖振力矩;C、C、CM′分别为阻力系数、升力系数和力矩系数对风攻角求导;χD、χ、χL、χL′、χM和χM′为气动导纳;u*（t）、w*（t）为脉动风在水平方向和垂向的分量;其他符号同前.对于较为钝化的截面，气动导纳函数偏安全地取1.0.

当计算列车风荷载时，上述公式中的（t）应替 换成合成风速（t），见公式（9）.

2.2 列车动力学模型

ICE3型列车模型在SIMPACK 软件中建立，列车的具体参数见文献[15]，单节列车模型为二系悬挂 四轴列车，包含 4个轮对、2个转向架和1个车体，各个刚体通过弹簧和阻尼连接，共 7个刚体，在软件中列车模型如图2所示.悬挂系统分为一系悬挂、二系悬挂，一系悬挂由轴箱弹簧、轴箱减震器等组成，用于转向架与轮对之间的连接;二系悬挂主要由空气弹簧、横向减振器、抗蛇行减振器等组成，用于车体与转向架之间的连接.为确保建立的列车运动接近 现实情况，各个刚体均考虑6个自由度，其中各个自由度分别为伸缩、横摆、浮沉、侧滚、点头、摇头，因此 单节列车一共 42个自由度.

2.3 桥梁、轨道结构动力模型

本文使用的桥梁为在建的金海特大桥，为多塔多跨斜拉桥，全长1369m，跨径布置为（58.5+116+3×340+116+58.5）m，主箱采用单箱三室截面，顶板采用正交异性钢桥面板，主梁断面高度4.5m，桥面 总宽 49.6 m，中间钢箱梁宽17.6 m，两侧挑臂式桥面 宽16 m，整体布置图如图3所示.大跨度斜拉桥和轨道有限元模型均使用有限元分析软件 ANSYS 建立，桥梁前10阶频率见表2.对建立好的模型进行子结构分析，得到所需的刚度矩阵和质量矩阵，通过ANSYS与SIMPACK 之间的程序接口，最终以柔性体和柔性轨道的形式分别建立斜拉桥和轨道的动力分析模型，并使用扣件将轨道与主梁连接起来，通过弹 簧-阻尼来模拟扣件.根据我国《高速实验列车技术 条件》中的建议，计算时采用德国轨道低干扰谱模拟 不平顺功率谱，空间步长为0.2m.本文列车采用单 列8 车编组（拖车+6动车+拖车）的高速列车模型，为了避免由于弹性轨道体过短而导致列车上桥、下桥 瞬间动力响应发生突变，轨道模型分为3部分：桥前 轨道模型（长度216 m）、桥上轨道模型和桥后轨道模型（长度216 m）.

2.4 车-轨-桥耦合模型验证

为验证本文建模方法的正确性，采用文献[16]中的桥梁、轨道和列车参数，利用本文中的轮轨耦合方法建立车?轨道?桥耦合振动分析模型[17]，计算了1节拖车以300km/h 通过桥梁时，桥梁跨中和钢轨跨中的竖向位移.文献[16]中也验证了SIMPACK与ANSYS 仿真分析的正确性.将本文计算结果与文献[16]和文献[17]对比，如表3所示，结果吻合较好，误差在3%以内，可以证明本文计算结果的准确性.

3 非平稳风对列车-大跨斜拉桥耦合系统动力响应影响分析

本文对现有实测台风数据采用上述风场模拟方法获得了非平稳台风风速时程，另外采用谐波合成法模拟得到平稳风速时程，图4给出了时距为10min的非平稳风在顺风向的时程曲线.对第一个模拟点的非平稳风速脉动部分进行快速傅里叶变换（FFT），并与Kaimal 谱进行比较，得到顺风向脉动风速功率谱密度如图5所示.

由图5可知，模拟得到脉动风速的模拟功率谱与目标谱，除在最低频率部分外，吻合非常好.

3.1  非平稳风对列车动力响应影响分析

在轨道不平顺的激励下，经过桥梁时会产生振动，列车的振动通过轮轨传递至主梁上，导致大跨斜拉桥也发生振动，而大跨斜拉桥的振动又会通过轮 轨传递到车体.对于列车而言，通常采用安全性和舒 适性指标来反映其动力响应.本文分别计算非平稳风和平稳风对耦合系统动力响应的影响，列车舒适 性指标主要考虑列车车体的加速度.为使结果更加直观，直接比较两种风环境下的车体加速度的时程曲线.由于拖车质量小、响应大，因此给出拖车在大跨斜拉桥上以300km/h的速度运行时两种风环境下的加速度时程曲线，结果如图6所示.随后将加速度时程曲线进行快速傅里叶变换（FFT），得到加速度的频谱图，如图7所示.

由图6可知，首先两种风环境下列车的加速度趋势基本一致，但加速度的峰值却有一定的差距.非 平稳风与平稳风作用下桥上列车车体的最大横向加速度分别为0.923m/s2和0.823m/s2，增长幅度约为12%;而竖向加速度分别为0.712m/s2和0.576 m/s2，增长幅度约为23%.这表明非平稳风作用下列车加速度的峰值会有一定的增加.在本文中列车横向和竖向最大加速度分别增加了0.1m/s2和0.136 m/s2，而 车体加速度属舒适性指标，因此非平稳风作用下会导致行车舒适性降低.

由图7可知，车体横向加速度在非平稳风和平 稳风作用下对应的一阶横向频率均为0.94Hz，但非 平稳风产生的振动在低频区域内比平稳风更加突 出;而车体竖向加速度的情况也是相同的，它们的一阶竖向频率均为0.88Hz，在低频区域内非平稳风引 起的振动更加明显，因此非平稳风作用下列车的振动频率和平稳风作用下是相同的，但在低频范围内 非平稳风引起车体的振动更加强烈.

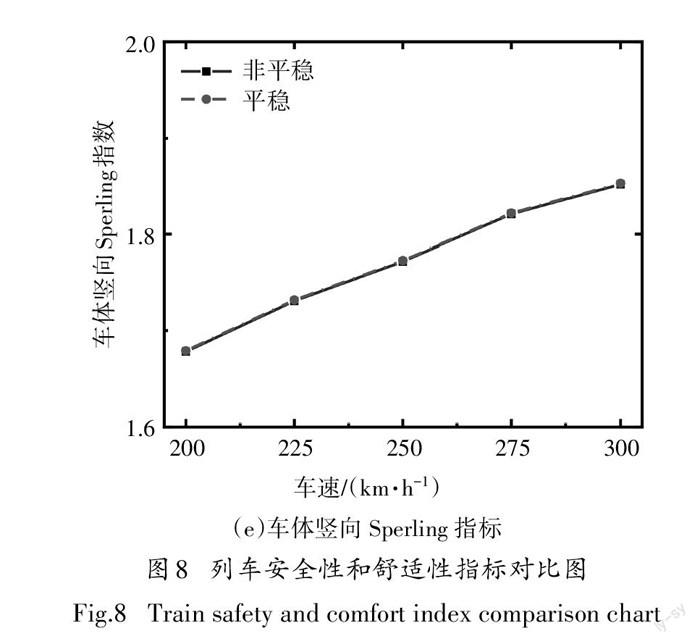
本文列车行车的安全性指标主要包括：轮重减 载率、轮轨横向力和脱轨系数.本文采用Sperling 指 标来评价乘客乘车的舒适性.列车在大跨斜拉桥上以200～300km/h行驶，受到非平稳风与平稳风作用，列车的安全性和舒适性指标如图8所示.

由图8可知，安全性和舒适性指标均随着列车 车速的增大而提高，其中轮重减载率在列车车速超 过225 km/h时就超过了规范限值，其他指标均在规范限值以内.当列车车速低于250km/h时，非平稳风 作用下，列车的安全性指标略有增大;当列车车速达到275 km/h 后，列车的轮重减载率和轮轨横向力表现出较大的差异，以车速300km/h为例，非平稳风作用下，列车的3种安全性指标分别为0.905、75.1kN和0.336，平稳风作用下的数值分别为0.827、73.3kN和0.323，增幅分别约为9%、14%和4%，故非平稳风会使桥上行车的安全性更差.然而不同种类风作用下列车的竖向Sperling 指标没有明显变化，这是因为计算中风速的竖向分量大小相差很小;而非平稳风 作用下车体横向Sperling 指标有一定的增大.

3.2 非平稳风对大跨斜拉桥动力响应影响分析

对于大跨斜拉桥而言，本文采用加速度来评价 其动力响应.同样地先给出四塔斜拉桥中跨跨中处的加速度时程曲线，结果如图9所示.同样地将主梁跨中加速度时程曲线进行快速傅里叶变换（FFT），得到加速度的频谱图，如图10所示.

由图9可知，两种风环境下桥梁的横向加速度曲线变化趋势基本保持一致，非平稳风对应的变化幅度更大且最大横向加速度为0.344 m/s2，而平稳风对应的最大横向加速度为0.296 m/s2，变化幅度约为16%;而在竖向最大加速度方面，非平稳风和平稳风 作用下分别为0.176 m/s2和0.165m/s2，变化幅度约为7%，因此非平稳风会增大桥梁加速度.

由图10可知，在低频区域内，对比平稳风，非平 稳风对桥梁产生的横向振动更剧烈，而桥梁横向加速度在非平稳风和平稳风作用下桥梁的一阶横向频率为0.93Hz，这和列车横向加速度的一阶横向频率0.94Hz 十分接近，因此列车过桥时发生过车桥共 振;在桥梁竖向加速度方面，两种风作用下桥梁的一阶竖向频率为0.28Hz，这和桥梁自身的一阶对称竖弯频率0.285 5Hz几乎完全一致，但在此频率处平稳 风对桥梁产生的振动比非平稳风更大，而在高频区域内两种风没有明显区别.

4结论

本文通过数值模拟技术模拟得到了非平稳台风 风场，并建立了高速列车-大跨斜拉桥耦合振动分析模型，开展了非平稳风与平稳风作用下车-桥系统动力响应影响分析，所得主要結论如下：

1）对列车系统而言，在非平稳横风作用下，斜拉 桥上运行的列车加速度会增大，经比较列车横向和竖向最大加速度增大幅度分别约为12%和23%，因 此非平稳风横风作用下列车的行车舒适性会明显降 低;通过频谱分析可以发现，非平稳风和平稳风作用下列车的一阶振动频率相同，但在低频范围内非平 稳风对列车产生的振动更强烈;比较两种风环境下列 车的安全性指标，非平稳台风会使列车的轮重减载率、轮轨横向力和脱轨系数增大，相比于平稳风，增长 幅度分别约为9%、14%和4%，因此非平稳台风会使 桥上行车的安全性更差;此外列车的Sperling指标仅在横向表现了差异，在竖向没有表现出明显的差异.

2）对桥梁系统而言，在非平稳横风作用下，斜拉 桥跨中处的加速度会增大，经比较可知，中跨跨中横向和竖向最大加速度增大幅度分别约为16%和7%;桥梁竖向加速度频谱图表明，在非平稳风和平稳风 作用下桥梁和列车在横向的振动频率相同，两者可能发生共振;而竖向加速度频谱图显示，在低频区域 内平稳风对桥梁引起的振动比非平稳风更加强烈，并且振动的频率刚好与桥梁本身的一阶对称竖弯基 频接近.

参考文献

[1]洪新民.侧风下考虑双车交会气动效应的高速列车-大跨度斜拉桥耦合振动研究[D].长沙：中南大学，2020：1-2.

HONG X M.Study on the coupled vibration of high-speed train and long span cable-stayed bridge system under the aerodynamic effect of trains passing each other in crosswind [D].Changsha： Central South University，2020：1-2.（In Chinese）

[2]韩艳，陈浩，刘跃飞，等.桥梁抖振力空间相关性对风-车-桥耦合动力响应的影响[J].湖南大学学报（自然科学版），2015，42（9）：82-88.

HAN Y，CHEN H，LIU Y F，et al.Effect of the coherence of buf-feting forces of bridges on the coupled dynamic responses of wind-vehicle-bridge system[J].Journal of Hunan University（Natural Sciences），2015，42（9）：82-88.（In Chinese）

[3]夏禾，陈英俊.风和列车荷载同时作用下车桥系统的动力可靠性[J].土木工程学报，1994，27（2）：14-21.

XIA H，CHEN Y J.Dynamic reliability of train bridge system un-der wind action [J].China Civil Engineering Journal，1994，27（2）：14-21.（In Chinese）

[4]郭向荣，曾庆元.京沪高速铁路南京长江斜拉桥方案行车临界风速分析[J].铁道学报，2001，23（5）：75-80.

GUO X R，ZENG Q Y.Analysis of critical wind speed for running trains on a schemed Yangtze River Bridge at Nanjing on Jing-Hu high speed railway line[J].Journal of the China Railway Society，2001，23（5）：75-80.（In Chinese）

[5]李永乐，强士中，廖海黎.考虑车辆位置影响的风-车-桥系统耦合振动研究[J].桥梁建设，2004，34（3）：1-4.

LI Y L，QIANG S Z，LIAO H L.Study of coupling vibration of wind-train-bridge system with regard to train location effect[J].Bridge Construction，2004，34（3）：1-4.（In Chinese）

[6]李永乐，强士中，廖海黎.风-车-桥系统空间耦合振动研究[J].土木工程学报，2005，38（7）：61-64.

LI Y L，QIANG S Z，LIAO H L.3-d coupled vibration of wind-vehicle-bridge system[J].China Civil Engineering Journal，2005，38（7）：61-64.（In Chinese）

[7]韩艳，刘叶，黄静文，等.考虑车桥间气动干扰的桥上车辆行驶安全性分析[J].湖南大学学报（自然科学版），2019，46（7）： 76-85.

HAN Y，LIU Y，HUANG J W，et al.Traffic safety analysis of ve-hicles on a bridge considering the aerodynamic interference be-tween vehicles and bridge[J].Journal of Hunan University（Natu-ral Sciences），2019，46（7）：76-85.（In Chinese）

[8]MONTENEGRO P A，HELENO R，CARVALHO H，et al.A com-

parative study on the running safety of trains subjected to cross-winds simulated with different wind models[J].Journal of Wind Engineering and Industrial Aerodynamics，2020，207：104398.

[9]劉庆宽，杜彦良，乔富贵.日本列车横风和强风对策研究[J].铁道学报，2008，30（1）：82-88.

LIU Q K，DU Y L，QIAO F G.Train-crosswind and strong wind countermeasure research in Japan[J].Journal of the China Rail-way Society，2008，30（1）：82-88.（In Chinese）

[10]TAO T Y，WANG H，WU T.Comparative study of the wind char-acteristics of a strong wind event based on stationary and nonsta-tionary models[J].Journal of Structural Engineering，2017，143（5）：04016230.

[11]WANG H F，WU T.Hilbert-wavelet-based nonstationary wind

field simulation：a multiscale spatial correlation scheme[J].Jour-nal of Engineering Mechanics，2018，144（8）：04018063.

[12]LOMBARDO F T，SMITH D A，SCHROEDER J L，et al.Thun-derstorm characteristics of importance to wind engineering [J].Journal of Wind Engineering and Industrial Aerodynamics，2014，125：121-132.

[13]HE X H，SHI K，WU T.An efficient analysis framework for high-speed train-bridge coupled vibration under non-stationary winds[J].Structure and Infrastructure Engineering，2020，16（9）：1326-1346.

[14]劉焕举，韩万水，武隽，等.大跨径桥梁三维台风风场数值模拟[J].振动与冲击，2017，36（24）：77-84.

LIU H J，HAN W S，WU J，et al.Numerical simulation of three-dimensional hurricane wind field around a long-span bridge[J].Journal of Vibration and Shock，2017，36（24）：77-84.（In Chi-nese）

[15]陈春霞.侧风下高速列车交会车-轨-桥耦合系统振动响应分析[D].长沙：中南大学，2019：23-24.

CHEN C X.Vibration response analysis of train-track-bridge cou-pling system under the action of high-speed trains passing each other in crosswind [D].Changsha：   Central South University，2019：23-24.（In Chinese）

[16]杨子云.汽车撞击荷载下列车?轨道?桥梁耦合振动精细化仿真分析[D].长沙：中南大学，2016：36-37.

YANG Z Y.The refined simulation analysis of coupled vibration of train-track-bridge subjected to motor collision loads[D].Chang-sha：Central South University，2016：36-37.（In Chinese）

[17]HAN Y，LIU Y，HU P，et al.Effect of unsteady aerodynamic loads

on driving safety and comfort of trains running on bridges[J].Ad-vances in Structural Engineering，2020，23（13）：2898-2910.