基于GeoGebra的高中数学建模案例研究

【摘要】在高中数学建模课堂教学实践中，充分应用GeoGebra能有效推动高中数学建模教学的真正实施，是提高数学建模教学效果的新途径.以具体的案例为例，感受GeoGebra应用于高中数学建模的技术优势，体会具体操作的技术路径;从研究教材内容适切点、构建教学范式、学生主动实践方面，阐述如何在日常建模教学中提升师生使用GeoGebra的能力.

【关键词】数学建模;GeoGebra;课堂教学

随着国家一系列提升教育现代化水平政策的出台，信息技术与教育教学融合的发展经历了起步阶段、应用阶段，逐步步入整合阶段和创新阶段[1].GeoGebra是一个集代数计算功能、图形计算功能、几何作图功能、概率统计功能于一体的免费数学信息技术工具.它具有适用于多种操作系统、数学功能完整、操作相对简单、可以用中文输入命令等优点，延伸了学生的双手和大脑，拓展了师生的视野和能力.因此，在高中数学建模课堂教学实践中，充分应用GeoGebra，能有效推动高中数学建模教学的真正实施，是提高数学建模教学效果的新途径.

1GeoGebra应用于高中数学建模的技术优势

1.1函数模型——代数运算和数形结合

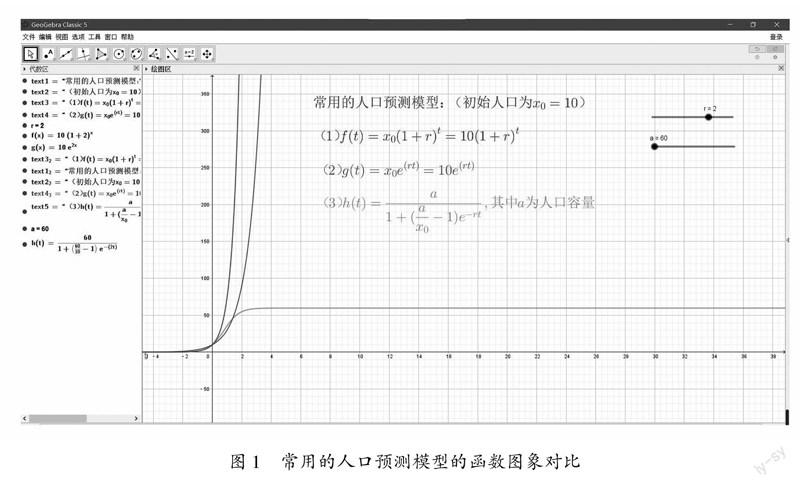
GeoGebra计算区具有数值计算、因式分解、方程求解、求导求积分等功能;绘图区有点、直线、曲线、多边形、圆、圆锥曲线、角度、滑动条等多种绘图及绘图辅助功能，此外命令输入功能让绘图和计算功能更加灵活.这些功能应用在数学建模的函数模型教学中能帮助学生直观观察函数图象，归纳函数的性质，近而通过逻辑推理进行证明.

如在人口增长模型的教学中，可以用GeoGebra绘制三种函数对应的图象，根据实际问题，理性的选择相应的函数进行拟合（见图1）.

1.2几何模型——直观可视

GeoGebra的动态几何功能应用最为广泛，它不仅可以作出规则图形、函数图象等二维几何图形，3D作图区还可以用于绘制三维图形，用户可以根据数学建模基础知识和GeoGebra丰富的命令功能绘制三维动态图形.这一功能为数学建模课程中几何模型的教学提供了直观可视的教学体验，通过可视化的呈现形式突出问题要点、克服理解难点.例如在地月模型的教学中，可以通过GeoGebra展现出地球与月球的动态几何抽象模型，帮助学生理解几何模型形成的过程（见图2）.

1.3概率模型——仿真模拟

GeoGebra还有强大的仿真模拟功能，能对一些常用的概率模型进行3D仿真试验，用仿真试验代替真实试验，既能直观展示又能规避实际操作的诸多困难与不便.如人教A版必修二教材中例题：从你所在的班级任意选出6名同学，调查他们的出生月份，假设出生在1月、2月……12月是等可能的，设事件A=“至少有两人出生月份相同”，设计一种试验方法，模拟20次，估计事件A发生的概率.我们就可以用Geogebra概率功能进行仿真模拟：输入命令“序列[序列[random（1，12），i，1，6]，i，1，20]”，形成一个列表，列表内是用于模拟6名同学的出生月份的1～12范围内的随机数，以6个数字为一行，每一行为一组，共20组，相当于模拟了20次.输入命令“条件计数[长度[互异[p]]<6，p，m1]”，计算出20组随机数中有相同数据的组数a，用于模拟事件A“至少有两人出生月份相同”在20次模拟中出现的频数.输入命令“a/20”即可计算出在1次仿真模拟试验中事件A发生的频率b.按F9可以快速重复本次的仿真模拟，得到多次仿真模拟实验结果（见图3）.

事件A发生的频率此外，我们还可以利用绘图区按钮编程中相应的脚本功能，将多次仿真模拟所得频率显示在同一图象中，通过CAS计算事件A發生的概率约为0.78，从而得到事件A在每次仿真模拟中的频率稳定在事件A发生的概率（约为0.78）附近（见图4）.

1.4Geogebra的多变量分析功能用于模型拟合

Geogebra的多变量分析功能可以用于对有效数据进行分析、模型拟合和检验.如研究茶水温度随时间变化数据时，利用Geogebra双变量分析功能对下表中的一组数据进行模型拟合.

Geogebra表格区创建新表格，将时间和水温数据填入.选中时间和水温数据，点击变量分析按钮选择双变量分析，画出散点图.

Geogebra自带丰富的回归模型，如线性模型、对数模型、多项式模型、幂函数模型、指数函数模型、成长曲线模型、正弦函数模型以及逻辑模型，可以对数据进行直接拟合，如下图为指数函数回归模型：

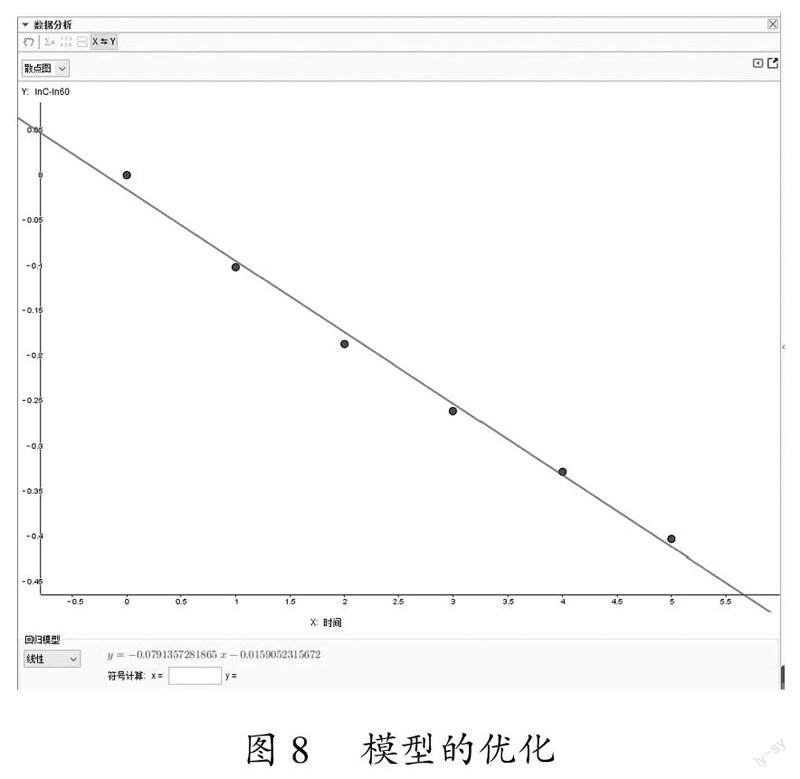
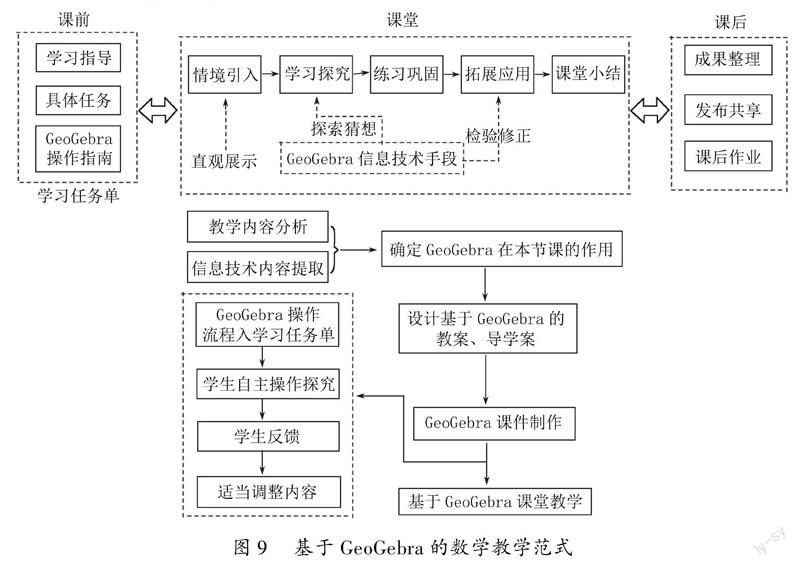
这些模型均会出现随着时间增加，茶水降至负值的现象，显然与事实不符.因此，在进行拟合操作时仅服从数据是不够的，还需要结合生活实际修正模型，考虑到茶水温度降至室温就不能再降的事实，可以选择函数y=kat+25（k∈R，0

选中A列、D列，利用双变量分析功能进行线性拟合，得到lna≈-0.0791，lnk≈4.0784，从而得出

a≈e^-0.0791≈0.9239，k≈e^4.0784≈59.0509.

根据实际情况可知，当t=0，y=85，可直接得到k=60，因此上述过程可进一步优化为ln（y-25）-ln60=tlna，再次进行双变量分析，得到的lna值差别不大.所以我们确定k=60，a=0.9239，就得到了一个模型y=60×0.9239t+25（t≥0）.

2反思与总结

通过信息技术与高中数学建模课程的深度融合，可以使学生用数学语言表达现实世界，发现和提出问题，感悟数学与现实之间的关联，积累数学实践的经验，认识到数学模型在科学、社会、工程、技术等诸多领域的作用，培养学生的创新精神和科学精神.结合当下高中数学建模教学现状，笔者提出以下三点建议：

2.1找准信息技术与教材内容的适切点，深入挖掘GeoGebra技术功能

GeoGebra虽然操作简单，但要完成更加复杂的任务，需要教师进一步学习以提高技术应用手段.教师可以从GeoGebra的论文、著作及官方网站中获取资源，或者从中国大学生MOOC等网站观看视频课程.新教材也更加重视用信息技术手段来发现、探究、解释数学知识，教师可以找准 GeoGebra与教材的适切点，开发并记录典型的基于GeoGebra的教学片段和案例，在此过程中对GeoGebra技术手段进行深入挖掘以优化教学效果，探究GeoGebra与高中数学建模课堂的最佳融合方式.

2.2构建基于GeoGebra的教学范式，积极变革数学课堂教学结构

利用GeoGebra等信息技术可以实现循环证明，在探索—猜想—检验—修正—证明的循环中，GeoGebra有利于实现其中的几步或全部[2].因此，根据GeoGebra在数学教学中的作用，开发基于GeoGebra的数学教学范式，以改变现有的数学课堂讲授模式，达成多元表征的呈现和联结.

2.3从观察参与到应用实践，让学生逐渐成为GeoGebra的应用主体

目前GeoGebra应用于数学课堂一般都是教师展示，学生观看学习.为了提高学生的参与度，可在学习任务单中加入相应的GeoGebra案例操作步骤，让学生按照步骤进行实践，尝试用GeoGebra探究、解释数学问题;此外，还可以开发GeoGebra建模校本课程，让学生对GeoGebra的更多基础功能进行系统学习，为学生提供一定的基础建模题目进行实践，促使学生探索GeoGebra的高级应用功能，让学生成为GeoGebra的应用主体.

参考文献

[1]宁连华，崔皓翔.信息技术与数学教学的深度融合研究评析[J].江苏教育，2020（04）：19-23.

[2]刘怡轩.GeoGebra在中学数学教学中的应用与展望[J].中学数学教学参考，2021（05）：42-44，54.

作者简介李现勇（1976—），男，山东青岛人，正高级教师，青岛市高中数学教研员，山东省特级教师，齐鲁名师，苏步青数学教育奖获得者，中国教育学会领航计划专家，人民教育出版社高中数学新教材培训专家，人民教育出版社教材核心编写者、《必修一教師教学用书》副主编;曾获教育部基础教育课程改革教学研究成果二等奖.