构造全等或相似 巧解特殊角问题

侯冠羽

一、具备条件

1.已知或结论中有 90°角、45°角或 60°角;

2.角的顶点在坐标轴或与坐标轴平行的直线上.

二、突破方法

总体思路：构造全等模型或相似模型.

1. 90°角

方法一：构造“一线三垂直”的全等模型;

方法二：构造“一线三垂直”的相似模型.

2. 45°角或 60°角

方法一：将 45°角或 60°角构造在直角三角形中，再回到 90°角的处理方式;

方法二：直接构造“一线三等角”的全等模型或相似模型.

三、经典变式

1.已知正方形 90°角;2.已知等边三角形 60°角.

四、典型例題

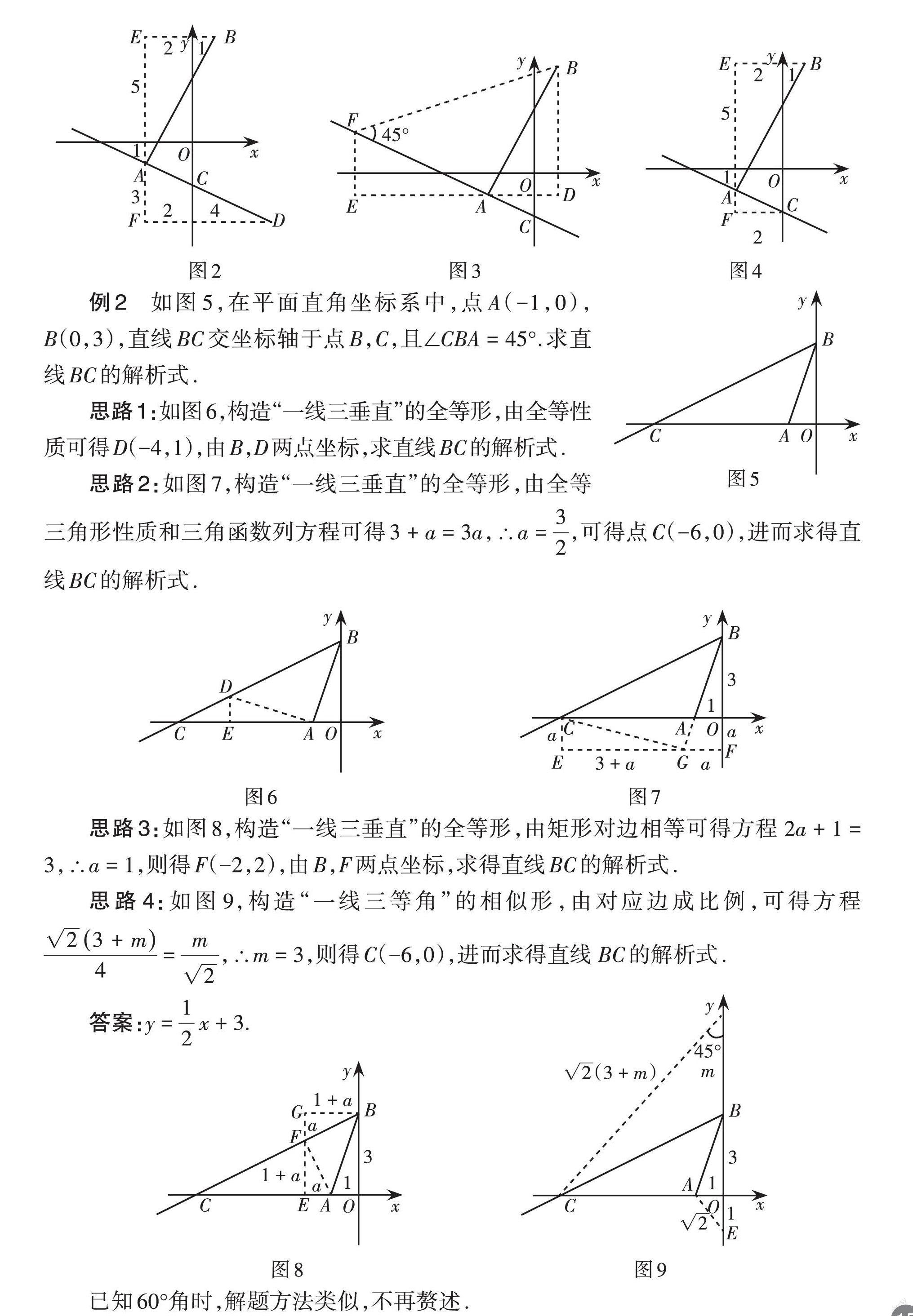
例1 在如图1，平面直角坐标系中，点 A（-2，-1），B（1，5），直线AC⊥AB交y轴于点C，求直线AC的解析式.

思路1：如图2，构造“一线三垂直”的全等形，易得点D的坐标是（4，-4）， 利用A，D两点求解析式即可.

思路2：如图3，构造“一线三垂直”的全等形，易得点F的坐标是（-8，2），利用A，F两点求解析式即可.

思路3：如图4，构造“一线三垂直”的相似形，易得点C的坐标是（0，-2），利用A，C两点求解析式即可.

答案：y = [-12x] - 2.

例2 如图5，在平面直角坐标系中，点A（-1，0），B（0，3），直线BC交坐标轴于点B，C，且∠CBA = 45°.求直线BC的解析式.

思路1：如图6，构造“一线三垂直”的全等形，由全等性质可得D（-4，1），由B，D两点坐标，求直线BC的解析式.

思路2：如图7，构造“一线三垂直”的全等形，由全等三角形性质和三角函数列方程可得3 + a = 3a，∴a = [32]，可得点C（-6，0），进而求得直线BC的解析式.

思路3：如图8，构造“一线三垂直”的全等形，由矩形对边相等可得方程 2a + 1 = 3，∴a = 1，则得F（-2，2），由B，F两点坐标，求得直线BC的解析式.

思路4：如图9，构造“一线三等角”的相似形，由对应边成比例，可得方程[23+m4] = [m2]，∴m = 3，则得C（-6，0），进而求得直线 BC的解析式.

答案：y = [12x] + 3.

已知60°角时，解题方法类似，不再赘述.