打破思维定式 感悟代数思想
2022-05-30房天营
房天营

【案例背景】
方程是小学阶段培养学生代数思想的重要载体,是学生由算术思维迈向代数思维的起点,所以方程在小学阶段具有极其重要的地位。方程是学生在经历了用字母表示数的过程,并且会寻找数量之间的等量关系的基础上学习的。然而,无论是用字母表示数,还是寻找数量之间的等量关系,对学生而言都是很抽象的,他们一下子很难接受代数思维,所以教学的难度很大。
【教学内容分析】
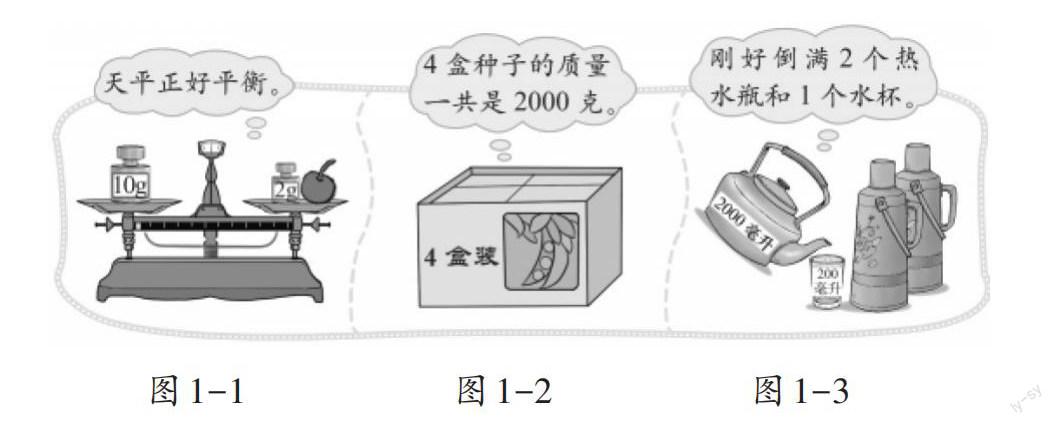
“认识方程”这节课的重点是要学生结合具体情境了解方程的意义,会用方程表示情境中的等量关系,并且经历将现实问题抽象成等式与方程的过程,学生在学习的过程中将积累等量关系符号化的活动经验。为了使学生体会方程是刻画现实世界的一个数学模型,激发学生的学习兴趣,教材编排了三个情境(如图1-1、1-2、1-3)和三个问题:
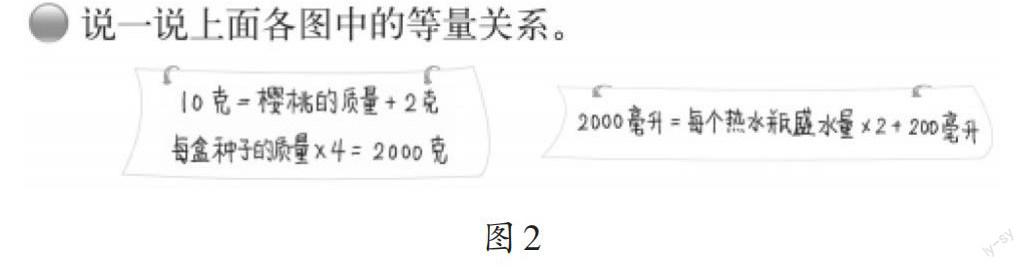
第一个问题是用口头语言描述上述情境中的等量关系(如图2)。
第二个问题是引入“用字母表示数”,引导学生用式子表示情境中的等量关系(如图3)。
第三个问题是观察上面表示等量关系所用的式子,抽象并概括出共同特征,从而认识方程(如图4)。
【教学回放】
师(出示图1-1):估一估樱桃的质量。
生1:我估计大约有10克。
生2:我估计大约有30克。
师:你们说的都是具体的数量,能不能用字母来表示樱桃的质量?
生3:樱桃的质量是n克。
生4:樱桃的质量是x克。
……
出示:
师:根据这幅图说一个式子。
生5:樱桃的质量+小砝码的质量=大砝码的质量。
师:现在樱桃的质量是x克,能列出一个式子吗?
生6:x+2=10。
[教学思考:借助天平直观演示平衡,说明两边物体的质量相等,学生说出等量关系后很容易列出等式。由实物演示到抽象式子的过程,学生的思维能力得到进一步发展。]
出示图6:
师:观察情境图,说出图中的数量关系。
生7:4块月饼的质量=380克。
生8:每块月饼的质量×4=380克。
生9:380÷4就等于每块月饼的质量。
师:如果每块月饼重y克,能列出一个等式吗?
生10:380÷4=y。
师(有点着急):没错,这是一个等式,但不是根据“每块月饼的质量×4=380克”来列的,还可以怎么列?
(学生沉默)
师:看黑板上的式子“每块月饼的质量×4=380克”,左边是什么?右边呢?怎么列式?
生11:y×4=380。
出示:4块月饼的质量=380克
4y=380
[教学思考:由天平过渡到电子秤,形式的变化使学生失去了直观的两端相等的参照,陷入了用算术法计算结果的惯性思维当中。尽管教师一再启发、提示,但学生由于没有学习方程,始终很难想到用方程式子表示等量关系。]
出示课本情境图:
师:看到这幅图,你会列式吗?
生12:(2000-200)÷2。
师:为什么这样列式?
生12:这样可以算出每个热水瓶能装900毫升水。
师:我们不需要计算出结果,只需要表示它们之间的相等关系。2个热水瓶的容量和1个水杯的容量正好是水壶的容量,应该怎样列式?
生13:2个热水瓶的容量+1个水杯的容量=水壶的容量。
师:如果每个热水瓶的容量是n毫升,怎样用式子表示?
生14:2×n+200=2000。
生15:2n+200=2000。
(教师根据板书的算式分类、归纳,揭示方程的概念。然而在练习环节,学生依然出现了“不列方程,而用算术方法直接算出结果”的现象。)
[教学思考:用语言表达等量关系本身就是教学的难点,更何况是这么复杂的等量关系,学生不能顺利说出等量关系也是意料之中。但教师没有更好的办法引导学生感受顺向思维的优势。]
出示图8:
生16:x+20=20+50。
出示图9:
生17:(11-7)÷2=x。
(有的学生干脆直接算出了结果)
【案例研讨】
在议课环节,评课教师给出了积极的评价:执教者语言幽默诙谐,尤其是肢体语言极为丰富,课堂上笑声不断,给学生营造了一个愉快的学习氛围;这节课的教学设计朴实而有新意,教学过程真实而生动,学生学得轻松又愉快。但是也提出了存在的问题:在揭示方程概念时,学生列方程表示的式子始终没能达到要求,虽然这是学生真实的学习状态,但是显然没有达到预期的教学效果。
学生在表示情境图中的等量关系时为什么不会顺向思维用方程表示,非得逆向思维用算术方法计算出结果呢?如何解决这一问题?
【案例分析及思考】
带着这个问题,笔者认真查阅了相關资料并积极和教研组的教师进行了探讨,得出以下几个方面的因素。
1.学生的思维定式。用算术方法计算结果是学生多年的习惯,因为从小学一年级开始,面对问题时,教师常这样提问:“要想求出这个问题,我们该怎么计算?”算术法已经成为学生的惯性思维,因而与新知造成冲突。而学生的认知与经验发生冲突,正是学习新知的一个契机,也是学习新知的增长点。对此,教师首先应认可等式380÷4=y,再引导学生利用字母表示数的知识进行讨论,最后得出4y=380。这样,先让学生明白同样的等量关系可以用不同的等式表达,再引导学生比较这两个等式哪个更好,更符合思维习惯。学生经过比较后也会得出“4y=380更好理解”的结论。
2.学生对于用字母表示数量和把字母当成已知数量参与运算不习惯。因为有了前一节的用字母表示数的认知基础,本节课的教学如果要充分链接旧知识,在涉及从数量等式到含有字母的等式时,就需要适当过渡一下。如一开始的天平平衡,两边都放入已知的砝码,左边放2个5克砝码,右边放一个10克砝码,让学生得出5+5=10,然后把一个砝码换成一个实物,假设它有x克,引导学生写出5+x=10。这样强化等量关系和等式的概念,便能唤醒学生的旧知,学生就能够从生活情境中提炼出方程模型,并用含有未知数的等式来表达等量关系。
3. 学生处在由具体形象思维到抽象思维的过渡时期。用天平演示时,学生很容易得出等量关系,并列出方程,而对于隐藏了天平的实物或图片,学生则不容易列出方程。这就充分说明了具体形象的东西,学生容易理解和接受,而对于需要进行分析和推理的概念,学生则难以接受和领悟。对此,可充分利用多媒体和各种直观的实物教具,先带领学生对等量关系及等式进行有目的地观察,让学生从具体的形象中区分哪些是主要的,哪些是次要的,找出它们之间的内在联系,再用形象生动的语言启发他们比较、分析和判断,找出其中的相同点和不同点,再归纳概括出等量关系与等式之间的本质属性,学生就能从形象思维过渡到抽象思维,列方程就会更加顺利。
4.提出的问题指向不明确。在出示4块月饼重380克的情境图之后,教师提出:“观察情境图,说出图中的数量关系。”接着又问:“如果每块月饼重y克,能列出一个等式吗?”这样的问题指向不够明确,学生的思考也就没有目的性。这里的问题可以更具体些,例如改成“根据情境图,我们可以找到一个等量关系,写出一个等式,那么在图中你还能找到另一块等量关系吗?”这样学生就能容易地说出“4块月饼的质量=380克”。教师再启发学生分析 “当一块月饼的质量未知时,我们可用字母x或y表示,那么能得出一个什么样的等式呢?”这样的引导更自然,学生用方程来表示也会水到渠成。
总之,教学方程知识,教师要根据教学内容和学生的思维水平,运用恰当的教学方法,提出切实可行的要求,对学生进行代数思维的初步训練。只有这样,才能让学生感悟和接受方程思想,从而与初中数学的学习接轨。“教学永远是一门遗憾的艺术”,但只要教师静下心来思考,蹲下身体了解学生,深度把握细节,有效突破难点,就会让课堂精彩而高效,也会让遗憾少一些。
(责编 金 铃)
