“用倒推的策略解决问题”学习路径优化的实证研究

王逸骏

[摘 要]“用倒推的策略解决问题”的教学目标是让学生能用自己的话解释倒推的过程，能在评论与讨论中找到方法，形成交流合作的能力以及逆向思维。文章以斯根普的理解模型为理论依据，得到了促进倒推策略教学的优化学习路径，并给出相应的教学建议。

[关键词]倒推;解决问题;学习路径;逆向思维

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2022）17-0008-04

一、引言

“解决问题的策略”（又称“还原问题”）是苏教版教材的重要内容之一。此内容的设置旨在让学生初步学会从数学的角度发现问题和提出问题，综合运用数学知识和其他知识解决简单的数学问题，发展应用意识和实践能力;获得分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，发展创新意识。

“倒推”是解决问题时经常用到的一种策略。在用“倒推”策略解决问题时，学生要进行分析、选择、判断、对比、优化等一系列复杂的思维活动。“倒推”策略，通俗地讲就是“倒过来想”，即从事情的结果倒过去想它在开始的时候是怎样的，教学的目的在于培养学生的逆向思维和发散性思维，提高其解决问题的能力。为了让学生能够真正掌握“倒推”的策略，必须探索出利于学生理解的学习路径，笔者把研究问题定为：教师预设的学习路径是怎样的？经过实践检验并优化过的学习路径是怎样的？如何验证学习的路径是否得到了优化？

二、研究设计

1.研究对象

根据学生的期末考试成绩和前测数据，发现苏州市S小学六年级甲、乙两个平行班的学生在数学学习水平上没有显著的差异。两次教学均由W教师承担，教龄4年。

2.研究流程

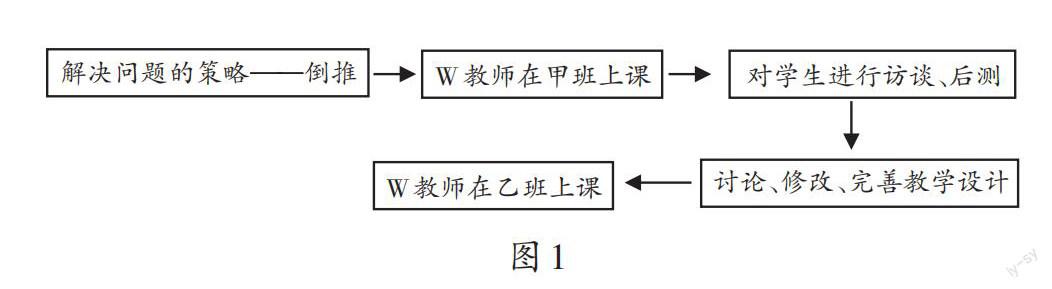
研究的主要步骤如图1所示：

主要采用课堂观察法、问卷调查法、访谈法、行动研究法来收集数据。来自教师的数据包括教学设计、教学录像、教学反思日志、课前和课后测试单。

3.对学生的后测

（1）理论模型

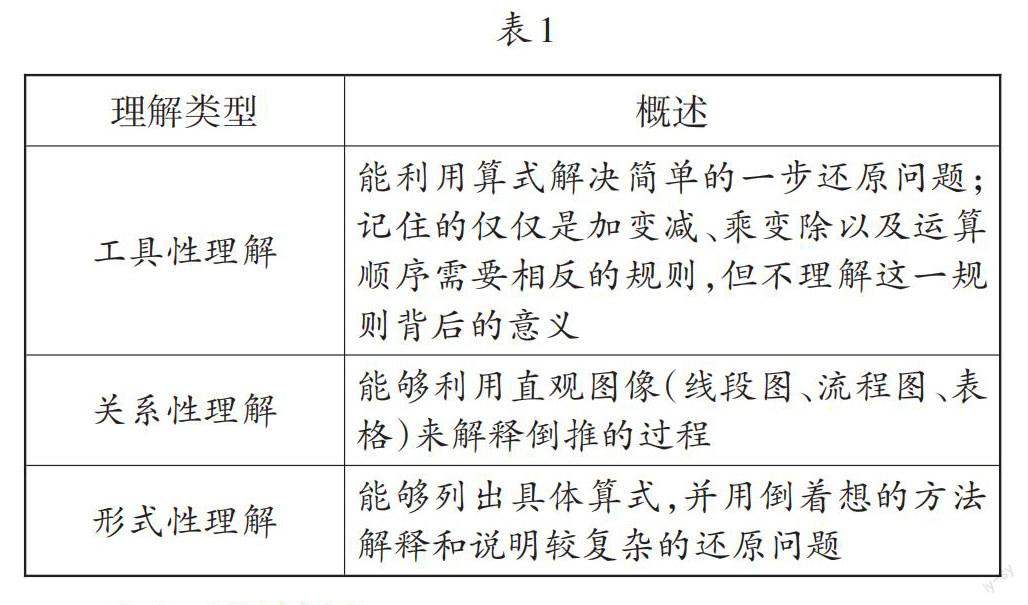
本文以斯根普的理解模型为理论依据，把学生的理解分为以下三种类型（如表1），以这三类理解为标准判断学生对倒推策略的理解情况。

（2）后测材料

用尽可能多的方法（可用文字、算式、画图等）表示解决以下问题的过程。

问题1 有一位老人说：“把我的年龄加上12，再除以4，接着减去15，最后乘10，恰好是100岁。”求这位老人的年龄。

问题2 学校运来36棵树苗，乐乐与欢欢两人争着去栽，乐乐先拿了若干树苗，欢欢看到乐乐拿得太多，就抢了10棵，乐乐不肯，又从欢欢那里抢回来6棵，这时乐乐拿的棵数是欢欢的2倍。问：最初乐乐拿了多少棵树苗？

问题3 粮库内有一批面粉，第一次运出总数的一半多3吨，第二次运出剩下的一半少7吨，还剩4吨。问：粮库内原有面粉多少吨？

问题4 粮库里有120吨面粉，第一次运出总数的一半多2吨，第二次运出剩下的一半少7吨，现在还有多少吨面粉？

问题5 结合问题3和问题4，说说在什么情况下需要用倒推的策略来解决问题。

（3）计分标准

根据学生的回答，参照表1的理解类型，对学生的理解进行分类并计分（如表2）。

三、结果与分析

1.学习路径A

（1）学习路经A的呈现

W教师独立备课，并在甲班上课。根据课堂实录，归纳出第一次设计与实施的学习路径A（如图2）。

首先，从前测已知学生对于简单的一步还原问题掌握得还是非常到位的，正确率高达94.59%，但是对于较复杂的类似于“几分之几多几”的多步还原问题，学生的正确率却只有62.16%。因此以简单的一步还原问题作为任务1，旨在让学生在教师的引导下通过直观表征的方式理解题中信息，进而用倒着想的方法解决问题，最后能够将理解的内容抽象为算式。

其次，出示任务2，旨在让学生在复杂情境中独立整理题目中的信息，用倒着想的方法解决问题，能够列出算式。

最后，出示任务3，旨在让学生在教师的引导下通过列表的方式整理信息，并用倒着想的方法解决问题，能够列出算式。

（2）教学效果

教学结束后，对甲班学生进行后测，学生不同理解类型的平均得分如表3所示。

工具性理解得分为0.324，说明部分学生对于还原问题还停留在表象阶段，记住的仅仅是加变减、乘变除以及运算顺序需要相反的规则，但不理解这一规则背后的意义。

关系性理解得分为0.432，而形式性理解得分为0.243，主要原因有以下三点：

①形式性理解对于学生而言认知难度较高;

②部分学生解题时需要借助线段图整理信息，但在复杂情境中无法将线段图直接转换成算式;

③W教师在课堂上过分强调用画图的方式整理信息，忽视了对学生倒着想的方法的引导和思维的训练。

（3）问题分析

①不会直观表征。学生是通过线段图来整理信息，进而列出算式的，而真正的直观理解应该是看图即可知道结果，不需要再次进行计算。

②难以抽象成算式。教师着重于信息的整理，对于倒着想的方法的引导比较少，进而使得学生抽象理解不到位，抽象成算式的能力较弱。

③分率问题对倒推造成干扰。任务1导致大部分学生陷入了“单位1”是否已知的怪圈，因为学生看到分数就自然而然想到了分数应用题，不会从倒推的角度去思考问题。

④时间分配不合理。任务1耗时过长，以至于后面的任务2匆忙，任务3来不及出示。

（4）改进建议

①替换任务1。教师发展指导者L在教学研讨中提出：任务1容易对学生造成干扰，使学生陷入解决分率问题的怪圈，并不适合放在课始，应当改为从整数出发的还原问题，并在学生提出用线段图或者流程图以后，补充列表的方法。这样一来，3种整理信息的方法都在任务1中有所体现，且从整数出发，学生不会将其與分率问题混淆，倒推的味道更浓，学生也更容易从倒着想的方法出发解题。

②增加对比练习。教师发展指导者Q在教学研讨中提出：还原问题的特点是已知现在的情况，探索原来的情况。但是现实中，还原问题不过是诸多现实问题中的一个种类，所以在教学新知后，需要出示两道对比练习题，让学生体会遇到什么类型的问题适合用倒推的策略去解决。

2.改进后的学习路径B

（1）学习路径B的呈现

经过对学习路径A的课后反思与讨论，W教师重新修改教学设计，在乙班实施了学习路径B（如图3）。

（2）教学效果

教学结束后，W教师对学生实施了后测，结果如表4所示。

比较表3和表4可以发现，学生的工具性理解的得分明显下降，形式性理解的得分显著上升，关系性理解的得分基本持平，这与教师有意识地引导学生倒着想并用自己的话解释倒推的过程这一设计是密不可分的。此外，形式性理解的提升还与教师有意识地引导学生进行对比练习，进而总结出还原问题的一般规律有关。总体来说，学生在还原问题的理解上取得了一定的进步，说明这一学习路径的优化确实可行。

四、结论与建议

1.结论

W教师预设的学习路径A中的任务1太过注重教授学生用画图的策略去整理信息，而忽视了对学生运用倒推策略的引导。在经过教师发展指导者L和Q的干预后，W教师重新进行任务单的设计。从不涉及分率的问题出发，启发学生用倒着想的方法去解决问题，让学生自由交流解决问题的具体过程，自然生成线段图、流程图、列表的信息整理方法，最后利用两道对比练习题（任务4）引导学生思考在什么样的情况下适合用倒推的策略解决问题。

对比甲、乙两个班学生的后测数据可知，优化学习路径后，学生工具性理解的得分明显下降，而形式性理解的得分显著上升。

2.建议

（1）弱化整理信息的策略教学

倒推策略和逆向思维的培养是本节课的教学重点和教学目标，但还有一个重要的过程性策略，那便是画图整理题中的信息。不少教师在教学时往往会本末倒置，习惯性依托画图来解释解决问题的过程，忽视了对于学生倒推策略和逆向思维的培养。因此，教师在教学该内容时要弱化整理信息的策略教学。

（2）任务设计的指向性要明确

如果任务设计从含有分率的还原问题出发，那么学生在思考如何解决问题时就容易从解决分率问题的角度入手，这样一来便不利于教学的开展。因此，教师在设计任务时指向性要明确，要有意识地引导学生从倒推的角度思考解决问题的方法。

（責编 金 铃）