学习科学视角下的数学空间游戏设计与应用研究

尚俊杰 曾嘉灵 周均奕

[摘   要] 空间能力是信息时代下人才培养的关键之一，与数学学習联系紧密，而立体图形的折叠与展开是中国小学数学图形与几何教学的重难点。教育游戏环境能够促进数学认知和空间能力发展。研究采用设计研究法，基于学习科学视角下教育学、心理学、认知神经科学在折叠与展开领域的相关研究成果，分析教育游戏相关理论构建认知、动机和调节的三维度游戏设计原则，设计开发了一款折叠与展开教育游戏《方块消消乐》，并开展应用研究对游戏的实际效果进行了评估。研究分析了32名学生的成绩数据发现，在每天40分钟共三天的基于游戏教学干预后，学生的数学知识学习和心理折叠能力显著提升，对于知识学习先验能力低的学生提升效果尤为明显。

[关键词] 学习科学; 教育游戏; 游戏化学习; 数学认知; 图形与几何; 空间能力; 折叠与展开; 心理折叠

[中图分类号] G434            [文献标志码] A

一、引   言

空间能力是人类的重要能力之一[1]，包含大量非语言认知能力，对于数学、工程、科学、技术能力等领域的成功至关重要[2-3]，尤其与数学能力联系紧密[4-6]。认知神经科学研究发现，人们在加工空间任务和数学任务时会激活相似的神经通路[7-9]，表明空间能力和数学能力的紧密联结可能基于更底层的共享过程。我国十分重视数学教育中空间与图形知识的培养，在《义务教育数学课程标准（2011年版）》（新课标）中将“图形与几何”作为数学课程内容的四大领域之一，强调“帮助学生建立空间观念”具有举足轻重的地位。

然而，图形与几何部分也是小学数学教学中比较薄弱的环节，一方面小学生的抽象思维和空间思维能力尚未发展完全，空间想象能力较弱，对平面图形和立体图形的正确表征难以建立;另一方面教师在进行相关知识教学时也难以表述，使其成了教学难点之一。其中，立体图形的折叠与展开更是难度排序第一的知识点[10]。研究发现，在折叠与展开的教学过程中，学生存在对于折叠与展开问题的想象困难;课堂教学中的动手操作只是流于形式;学生往往因课后练习出错率高，逐渐失去对几何的学习兴趣等[11]。

近年来，游戏化学习备受关注，“寓教于乐”的教育游戏不仅可以激发学习动机，还能够发展学生的认知能力[12]。此外，已有许多研究证实了游戏环境对空间能力的提升效果[12-15]。鉴于此，本研究以学习科学的多学科视角，基于教育学、心理学和认知科学领域的相关研究成果，对立体图形折叠与展开的教学内容、认知机制进行分析，设计开发了一款适合小学五年级“立体图形折叠与展开”内容学习的数学空间教育游戏《方块消消乐》（曾用名：《方块消消消》），并将该教育游戏应用于教育教学实践，对其应用效果进行了评估。

二、理论基础

（一）基于学习科学视角的折叠与展开学习

本研究从学习科学的跨学科视角出发，综述了教育学、心理学和认知科学领域相关理论和研究成果，深入系统地分析了折叠与展开的学习过程，为折叠与展开教育游戏科学、有效的认知活动设计提供理论基础。

1. 教育学视角

几何学习和空间能力发展是小学数学课程的重要内容之一。对于立体图形的折叠与展开这一学习内容，学习者需要掌握立体图形（如长方体、正方体）的特征、认识立体图形展开图、在展开图中找到各组相对的面等知识点[16]。在教学的过程中，教师需要重点关注学习者感受和想象将立体图形表面展开的过程，帮助学生感受图形在二维平面和三维立体之间展开和折叠的运动变化[17]。整个运动变化过程是学习的重点，同时引导学生深入了解立体图形的特征，培养学生的空间能力。

为了达到以上的教学目标，研究者们设计了剪纸盒、磁力片等多种教学方式[18-21]。已有研究也探讨了学生在学习折叠与展开内容时出现的问题及可能成因，如高晓旭认为，由于学生缺乏独立自主的操作训练、教师缺乏对学生想象过程的确切指导等原因，学生会出现难以想象立体图形变化过程、难以理解展开图与立体图面关系、难以描述折叠与展开动态过程等问题[11]。

因此，了解学生空间想象的认知过程是促进有效的数学学习和空间训练的关键步骤。学生对立体图形进行折叠与展开的过程，实际上是在进行心理折叠的过程，与心理折叠能力息息相关。

2. 心理学视角

心理折叠（Mental Folding）是一种复杂的空间可视化能力，是将二维的空间图形和对象通过心理操作，转换成三维的空间图形和对象的信息加工过程[22]。心理学相关研究从心理折叠能力的发展和认知层面分析了学生在心理折叠任务时的表现，关注学生对二维图形和三维物体的表征过程和加工模式。

心理折叠能力作为一种复杂的空间能力，会随着年龄的增大而逐渐提高，其中8至9岁是学生从二维图形认知向三维物体认知发展的重要阶段。有许多因素可能会影响学生的心理折叠表现，比如折叠与展开的方向。根据Tversky提出的功能空间模型[23]，物体附着在三个身体轴上，包括头/脚（head/feet）、前/后（front/back）和左/右（left/right）[24]。与左/右轴相比，有关头/脚轴或前/后轴上物体的信息可以更快地被检索到[25-26]。因此，学生较好处理前/后轴上的折叠，也比较好处理头/脚轴的折叠，较难处理左/右轴的折叠[27]。折叠过程中涉及的正方形数目也会对心理折叠任务难度产生影响，每次动作所涉及的正方形数目越大，其难度越大[28-29]。此外，立体图形的不同类型也会影响心理折叠的难度，其中立方体难度较小[30]，是学生认识立体图形展开图较好的切入点。

研究表明，空间能力可以通过与环境的交互得到发展[31]，同样心理折叠能力也可以通过训练提升，桌面游戏和计算机环境均对心理折叠能力的发展有促进效果[32]，如Yun等[33]发现，与传统教学方法相比，VGLS（虚拟几何学习系统）在提升中学生心理折叠能力方面具有明显优势。此外，教育游戏也是提升学生心理折叠能力的有效途径之一。从感知重组和学习的视角理解空间概念的发展[34]，技术可以通过约束、反馈和目标结构系统帮助学生从非正式的感知特征转变为更具规范性的特征[35]。而教育游戏可以为学生提供基于感知的体验，能够促进学生与概念本身的交互，有助于发展心理折叠能力[36]。

3. 认知神经科学视角

教育学和心理学分别从行为层面和认知层面分析了折叠与展开学习的过程，认知神经科学研究则从生理层面探究了折叠与展开学习的神经学基础。众多研究者应用脑成像技术研究学习者的大脑活动，探索心理折叠任务的基础神经结构。脑电研究证明，心理折叠与大脑的顶叶区域有着密切的关系[37-39]。此外，Dan和Reiner应用脑电图测量了学生在观看2D或3D折纸演示视频时的认知负荷指数，结果表明3D的演示视频能够显著降低学生的认知负荷指数[40]，同时提升心理折叠能力。据此，本研究在教育游戏中设计了3D脚手架以促进学生的认知，辅助学生想象二维图形和三维物体运动变化的过程，并减轻学生的认知负荷。

（二）教育游戏支持的折叠与展开学习

本研究立足于建构主义学习视阈，对教育游戏设计开发理论研究进行梳理。从教育游戏中的学习者信息加工模式、有效教学情境创设、学习动机激发和教师的促进引导作用四个方面讨论教育游戏设计原则，以认知、动机和调节三个维度建构教育游戏设计理论框架（见表1），为折叠与展开教育游戏的有效设计提供参考和支持。

1. 认知设计

多媒体学习认知理论（Cognitive Model of Multimedia Learning）总结了多媒体学习中的认知过程和心理表征，根据学习科学的三项基本原则，包括双通道原则、有限容量原则和主动加工原则，描述了多媒体环境学习是如何发生的[41-42]。当人们玩教育游戏时，可以在三种认知加工中分配有限的加工能力，包括无关加工、必要加工和生成加工。教育游戏在促进生成加工过程时起着重要作用，但容易产生无关加工过程。因此，教育游戏设计的目标是最大程度地减少无关加工，引发必要加工并促进生成加工。

由于教育游戏具有丰富的三维空间，教学内容主要通过视觉信息呈现，往往占据着学习者的视觉通道，因此在学习者与教育游戏进行交互时，同时进行有意义的听觉和视觉输入可能对学习者的注意力造成破坏[43]。好的教育游戏会使用环境音乐来调节听觉通道，但需要注意环境音乐和音效的有效设计，以减少无关加工。另外，由于学习者每次在一个通道内只能处理少量信息，应注意避免同时呈现过多的学习材料，增加学习者的认知负荷，以保证必要加工过程的顺利进行。

本研究基于多媒体认知理论，分析学习者在教育游戏中的信息加工模式，提出了教育游戏设计开发的认知设计原则，见表1中1-1、1-2。

2. 动机设计

情境认知理论认为，将学习置于知识产生和运用的特定物理或社会情境中，才可能发生有意义的学习。受情境认知理论的影响，教育游戏的设计主张将知识与情境融合，模拟真实的应用情境，设计虚拟的仿真场景，使学习者在与学习情境的交互中进行有意义学习，实现知识与技能的有效迁移。在教育游戏的设计中，可以通过给予玩家身份（Identity）吸引其思维，使其相信自己在游戏情境中是一个独特的个体[43]，促进学生在教育游戏中的投入。

心流理论（Flow Theory）指出，当人们在进行某些日常活动时会完全投入到情境当中，注意力高度集中，并且过滤掉所有与活动不相关的知觉，进入到一种心流状态[44-45]。心流是学习的最佳状态，可以通过内在满足感使学习者在从事任务时不停探索，不断达到新的目标，最大化提高学习效率和学习深度[46]。基于心流理论，在教育游戏的设计中应该遵循以下规律：（1）概念和内容的复杂性是逐渐增加的，随着个人技能水平的提高，挑战水平也随之提高，从而在无聊和沮丧状态之间产生动态的张力;（2）游戏的规则必须明确，使学习具有可复制性，帮助学生探索环境和物体;（3）向学生提供明确的目标;（4）向学生提供快速、清晰的反馈，使学生知道自身目前的进度，以及成功完成任务还需要做什么努力;（5）游戏界面设计（即用于操纵游戏的控件）尽可能清晰和用户友好，以减少无关加工[47-48]。

本研究基于情境认知理论和心流理论，分析内在动机的激发方式，提出了教育游戏设计开发的动机设计原则，见表1中的2-1至2-6。

3. 调节设计

Kolb提出了体验学习理论，用学习循环模型来表示体验学习的过程，主要包含四个步骤：具体体验、观察反思、形成抽象概念和在新情境中检验[49]。其中，反思是体验学习的核心，在教育游戏中鼓励批判性思维会影响更多长期记忆通道。当学习者利用现有知识库（模式）在教育游戏中学习时，将获得新的体验，并将其与他们先验的知识和经验联系起来，进行有效组织，从而吸收游戏中嵌入的学习内容，这就是学习者在教育游戏中的自我调节学习过程。在基于教育游戏的学习中，教师扮演着指导者的角色，负责促进和引导学习[50]。根据对教育游戏自我调节学习过程的分析，教师在课堂上应负责：（1）根据学习者独立完成任务的情况，创建知识脚手架;（2）设计小步子教学指导，为学习者提供表达和反思的机会;（3）在学习者完成所有任务前，提供学习支持，答疑引导。另外，为了及时给学习者提供学习支持与反馈、指导教学和评估学习，应根据教学需求，在教育游戏中设计恰当的数据收集点，以收集到需要的反馈、评价数据。

本研究基于体验学習理论，分析教师的促进引导作用，提出了教育游戏设计开发的调节设计原则，见表1中的3-1至3-4。

三、教育游戏设计研究

基于学习科学和教育游戏的理论基础，本研究设计开发了这款促进小学五年级学生折叠与展开学习的教育游戏《方块消消乐》。该游戏的设计围绕内容设计和游戏设计两个方面展开，其中内容设计是游戏整体设计的基础。游戏的设计框架如图1所示。

首先，在游戏的内容设计方面，本研究基于《义务教育数学课程标准（2011年版）》的学习内容标准和学段学习要求，开展了对人教版和北师大版教材的教学内容分析。经过整合分析结果，进一步总结与拓展，得到折叠与展开教育游戏的教学内容与组织顺序，基于此构建知识模块与框架，设计每个知识模块的认知活动，开发认知活动相应的学习资源，并针对学生认知困难的点设计脚手架，以支持学习。

其次，围绕着游戏的内容，贴合着目标概念学习，本研究开展了游戏总体元素的设计，包括故事背景的创设，搭建学习情境;设计游戏形式与规则玩法;体现游戏核心的功能模块设计;具体化游戏设计表现的场景交互设计。功能模块设计是教育游戏实现教育目标的重要部分，本游戏的功能包括任务功能、脚手架功能、反馈评价功能、成就收集功能和行为数据收集功能。游戏整体设计旨在使学习内容与游戏元素相互呼应，实现教育游戏内容概念与游戏的有效整合。相比于平衡游戏的教育性与游戏性，本研究旨在促进教育性与游戏性的融合发展。

（一）游戏内容设计

基于国家课程标准折叠与展开内容学习要求，本研究从目标定位、教学内容、教学序列和空间对象表征方面对两版教科书进行对比分析，确定采用正方体作为空间概念的表征方式，及以逐层递进、逐渐抽象的方式组织的三个教育游戏知识模块：展开图相对面的辨认、展开图前面与上面/下面的辨认、立体图形与展开图的对应。通过不同类型的任务对同一空间概念进行表征，为学生提供丰富的认知机会，促进学生思维发展。

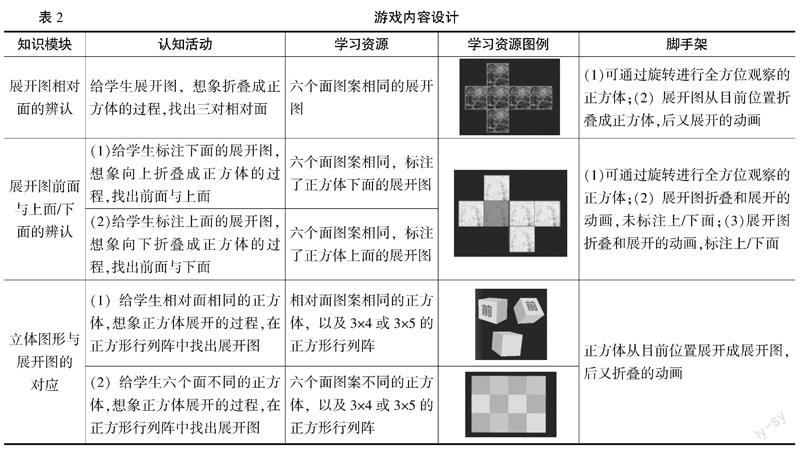
参考基于学习科学视角的折叠与展开学习研究，针对每个知识模块开展认知活动设计。为了给予学生想象图形运动变化过程的最大空间，所有学习活动均呈现静态平面图形与可观察的立体图形，将图形动态变化过程保留给学生进行想象。在认知活动设计中，综合考虑了学生的年龄特征与任务难度的影响因素。遵循学生的年龄发展规律，在学习过程中逐渐增加难度，实现学生思维从具体到抽象的过渡;考虑到折叠与展开方向和每次操作所涉及的正方形数目是影响任务难度的两个因素，对任务难度进行排序，并根据难度排序进行关卡设计。具体的认知活动设计见表2。

学生在教育游戏环境中通过学习资源直接与学习内容进行交互，构建空间概念表征，因此游戏的学习资源设计在内容框架和认知活动的基础上开展，主要为正方体平面展开图、可旋转观察的正方体及正方形行列阵，见表2。

为了帮助学生解决认知困难、促进学生对二维图形和三维物体运动变化过程的理解和表征，本研究设计了两种认知脚手架，分别为可旋转观察的正方体和二维图形与三维物体运动变化过程的演示动画。例如，在展开图相对面的辨认模块中，游戏提供了可通过旋转进行全方位观察的正方体，帮助学生建立对平面图形和立体图形的表征，辅助进行二维图形和三维物体表征的转换;以及展开图从目前位置折叠成正方体，后又展开的动画，帮助学生进行平面图形和立体图形转换的想象，突破认知困难。

（二）游戏整体设计

1. 故事背景创设

故事背景创设能够为学生提供在教育游戏世界中独特的个体身份，增强代入感，提升学习动机，是保证游戏其他设计效果的基础。《方块消消乐》将学生设定为勇闯混沌的库布（Cube）世界的勇士，并提供八款游戏化身选择，学生可以选择其一开始游戏，与邪恶势力斗争，找寻被封印的12神兽，守护库布世界。

2. 规则玩法设计

基于对学习者的分析，《方块消消乐》目标对象为小学五年级学生，为了在游戏过程中，尽量减少学生在操作和规则理解上的困难，应设定清晰明确的游戏规则，保持学生的注意力和兴趣，并将主要玩法设计得简单且易于操作。因此，本游戏采用消除游戏的形式，学生在游戏中会遇到基于每一关卡图形库随机生成的图形，玩家需要在限定的步数内消除足够多的正方形。根据每一个知识模块的任务要求，学生需在图形中找出、消除对应的面，如果选择正确，相应的面被消除，玩家累积得分，步数减少，进行下一个任务或图形挑战;反之，玩家的机会步数减少，进行同一个任务挑战。游戏结束，根据玩家得分进行总结性评价反馈，评判星级，并进行关卡物品奖励。

3. 功能模块设计

游戏的功能模块设计是支持教育游戏有效运作、达到教学目标的关键，《方块消消乐》游戏主要包括任务功能、脚手架功能、反馈评价功能、成就收集功能和学生行为数据收集功能。

其中，任务功能是教育游戏的核心功能，也是学生进行认知活动的功能。如前文所述，本游戏中包括三种任务：展开图相对面辨认任务、展开图前面与上面/下面辨认任务和立体图形与展开图对应任务，以闯关模式作为其具体表现形式，设计对应的三个地图：火焰山、冰川岛和水晶岩洞。

脚手架功能是支持学生进行折叠与展开学习，帮助突破认知困难的功能。如前所述，本游戏设计了两种脚手架支持：可观察的正方体和平面图形与立体图形变化过程动画，旨在帮助学生建立对平面图形和立体图形的表征，建构表征相互转换的过程。根据三种任务要求，设计渐进的脚手架，表现在游戏中为不同难易程度的提示，见表2。需要注意的是，当学生使用了正方体脚手架提示时，本次操作得分减半;当学生使用了折叠与展开动画脚手架提示时，本次操作不得分。

反馈评价功能是学生获得学习反馈以调整学习过程的功能，包括闯关过程中的实时反馈和闯关结束后的总结性评价反馈。闯关过程中的实时反馈表现在学生进行图形选择后，如果选择正确则图形消除、出现选择正确游戏音效、得到积分奖励，如图2（a）所示;如果選择错误则图形不消除、出现选择错误游戏音效、不积分，并显示错误提示，以帮助学生发现认知错误，及时构建正确概念，如图2（b）所示。总结性评价反馈发生在学生闯关结束后，对学生在这一关的学习表现进行评星打分，提供学习结果反馈。

成就收集功能是为学生设置的随机通关奖励，能够有效激发学生的学习动机。每个关卡都设有通关物品奖励，如地图碎片、护身符、神兽等，学生可以在背包处查看已获得的通关奖励。学生行为数据收集功能则是教师获得教学反馈、调整教学的重要参考，也是教育游戏评价的数据基础之一，能够提供客观有效的学习行为数据。本游戏设计了学生行为数据采集点，一方面记录关卡内学生的任务完成情况，包括学生每次操作的时间、图形、正误情况、选择情况等;另一方面记录学生关卡任务完成外的行为情况，包括提示、暂停、重新开始、背包等。

4. 场景交互设计

基于理论基础中确定的教育游戏设计理论框架，开展场景交互设计。《方块消消乐》共设计了9种场景界面，如游戏入口界面、关卡选择界面、游戏主界面、游戏结果界面等，每一种界面都承载着游戏的不同功能，共同组成了完整的游戏架构。

四、教育游戏应用研究

为了检验《方块消消乐》折叠与展开学习的效果，本研究将此游戏应用于小学五年级课堂教学，开展了实验研究，以评估《方块消消乐》对提升学生数学知识学习和心理折叠能力的效果。并尝试探究《方块消消乐》对具有不同先验能力的学生，是否会产生不同的影响效果。根据研究目的，本研究采用前后测实验设计，并提出两个研究假设。假设一：学生的知识学习和心理折叠能力后测成绩都显著高于前测成绩;假设二：对于先验能力低的学生，其知识学习和心理折叠能力的提升效果都显著高于先验能力高的学生。

（一）研究设计

1. 研究对象

本研究在北京市一所公立小学的五年级开展，随机选取了一个班级共37名学生参与实验，其中女生20名，男生17名。由于整个实验周期（包括前测、干预和后测）持续11天，存在一些学生无法完成整个实验的情況，所收集到的数据反馈不完全，无法纳入分析过程，作剔除处理。完整参与研究的总人数为32人，其中女生15名，男生17名。该所小学使用北京版教材，尚未完成“立体图形的折叠与展开”内容的学习。

2. 研究工具

为测量学生的知识学习成绩，研究参考小学五年级折叠与展开内容的习题和试题，在小学数学教育专家的指导下，开发了学习成效测试，共包含11道题目，分别为6道选择题和5道填空题。每道题目计1分，测试总分为11分，学生的测试成绩为正确回答题目的累计分数。针对前测和后测开发了两版学习成效测试，保持试题数目、类型、测试内容和难度相同，题目中具体图形和答案不同。

为评估学生的心理折叠能力，研究选取了应用最为广泛的纸张折叠测试（Paper Folding Test）[51]作为测量工具，共包含20道题目。测试总分为20分，学生的测试成绩为正确回答题目的累计数目减去错误回答数目的五分之一。测试题目被分为两部分，每部分有10道题目，呈现在同一页上，计时3分钟完成。每道题目给出一张正方形纸的折叠和打孔方式，学生需要想象打孔后的纸张展开过程，并在五个答案中选择展开后的正方形纸。

3. 研究过程

实验前测在实验干预的前一周进行，即第一天，学生进行了知识学习和心理折叠能力的前测，分别用时为14分钟和6分钟。在第八天至第十天，开展三天的实验干预，学生每天进行1课时的基于《方块消消乐》的学习，持续时间40分钟。第八天为新授课，由教师开展基于《方块消消乐》的折叠与展开内容教学;第九天和第十天为练习课，学生独立进行基于《方块消消乐》的学习，教师作为引导者的角色，为学生答疑解惑，提供学习支持。干预结束后，第十一天，学生进行知识学习和心理折叠能力的后测，用时与前测一致。

（二）研究结果

1. 教育游戏应用效果

本研究采用配对样本t检验对学生前后测数据进行分析，以探究教育游戏的应用效果。结果见表3，学生知识学习的后测总分均值（M=9.63，SD=1.29）显著高于前测（M=6.00，SD=2.78），t（31）=-8.618，p=0.000，d=1.524;心理折叠能力的后测总分均值（M=10.85，SD=4.23）显著高于前测（M=8.38，SD=4.33），t（31）=-5.075，p=0.000，d=0.897。研究结果证明了研究假设一，学生的知识学习和心理折叠能力后测成绩都显著高于前测成绩，说明教育游戏《方块消消乐》的应用能够提升学生的数学知识学习和心理折叠能力。

2. 不同能力学生对比

本研究采用独立样本t检验，对高先验能力学生和低先验能力学生的前后测分数差（后测—前测）进行分析，以探究教育游戏对具有不同先验能力学生的影响效果。由于样本量未达100人，本研究分别按照前测知识学习分数和心理折叠能力分数，以50%为界将学生分为高能力组（16名）和低能力组（16名）[52]。结果见表4，知识学习先验能力低的学生分数提升均值（M=5.31，SD=1.92）显著高于先验能力高的学生（M=1.94，SD=1.39），t（30）=-5.69，p=0.000，d=2.01;心理折叠先验能力低的学生分数提升均值（M=3.00，SD=2.84）与先验能力高的学生（M=1.95，SD=2.66）无显著差异，t（30）=-1.08，p=0.289。研究结果部分证明了研究假设二，对于知识学习先验能力低的学生，《方块消消乐》应用的提升效果显著高于知识学习先验能力高的学生;不过《方块消消乐》的应用对于心理折叠先验能力不同的学生，提升效果无显著差异。

五、结论与讨论

（一）研究总结

本研究基于学习科学视角设计开发了一款科学、有效、有趣的教育游戏《方块消消乐》。在学习方式上，游戏结合了学习科学领域对折叠与展开学习过程的研究结果，以遵循学生认知发展规律的方式有效建构空间概念;在学习内容上，游戏基于我国设定的课程标准与权威教材进行了详细的教学内容设计分析，以保证内容基础的适切性;在游戏设计上，本研究分析提出了教育游戏设计开发的认知设计原则、动机设计原则和调节设计原则，以实现教育性与游戏性的融合。在此基础上，本研究将游戏与课堂教学整合，开展了教育游戏的应用效果评价。结果显示，《方块消消乐》可以有效地提升学生的数学知识学习和心理折叠能力。在知识学习上，相比于先验能力高的学生，《方块消消乐》对先验能力低的学生提升效果更佳，而对于心理折叠能力来说，《方块消消乐》对于先验能力不同的学生具有相同的提升效果。

学习科学作为一个研究教与学的跨学科研究领域，整合了教育学、心理学、认知科学、脑科学等众多领域研究成果。如何将学习科学理论落实在具体的教育游戏设计中，以学习科学理论指导学生在教育游戏中学习，是每一个教育游戏实践者都必须要思考的问题。在教育游戏的设计开发中，实践者需要梳理学习内容，总结学生学习过程中遇到的问题与困境，然后以问题为锚点，分析学生认知规律与认知水平。以学习科学相关理论为基础建构教育游戏的整体逻辑框架，从而搭建理论与实践之间的桥梁。

（二）研究启发

回顾本研究可以发现，教育游戏设计是从理论到实践不断落地的过程。从理论研究开始，结合需求分析，最终完成游戏的设计与开发，以实现科学、有效、有趣的教育游戏。据此，本研究得出以下教育游戏设计的启发：

1. 理论研究是教育游戏设计开发基础

教育游戏设计开发过程的理论基础包括学习内容相关理论和教育游戏设计理论。学习内容相关理论能够帮助研究者了解学生的学习过程和认知方式，从而设计科学的认知活动支持学生的概念建构，保证教育游戏的科学性。本研究中《方块消消乐》的设计基于学习科学的跨学科研究成果，探究学生二维、三维图形表征建构和心理折叠能力认知过程，以及折叠与展开教育教学问题及成因，总结出设计开发教育游戏认知活动的理论基础。教育游戏设计理论是游戏总体设计的参考，为教育游戏的有趣性提供支持。本研究立足于建构主义学习视域，基于多媒体认知理论分析学习者在教育游戏中的信息加工模式，基于情境认知理论和心流理论分析内在动机的激发方式，基于体验学习理论分析教师的促进引导作用，从认知设计、动机设计、调节设计三个方面提出教育游戏设计开发的原则，为营造科学有效的学习环境提供支持。

2. 需求分析是教育游戏有效应用的保障

在研究目标内容相关理论的同时，应开展对目标知识内容的教学和学习的需求分析。通过需求分析，建构教育游戏设计开发的内容基础，贴合目标需求进行教育游戏的认知活动设计，从而保证教育游戏的有效性和实用性。本研究从中国数学课程标准出发，分析人教版和北师大版小学五年级数学教科书，梳理“立体图形折叠与展开”相关部分的教学设计思路，明确教学目标、教学内容和学习深度范围，为构建教育游戏的学习内容框架、设计符合学生认知发展的认知活动与相应的学习资源和脚手架提供参考。

3. 设计开发实现教育性和游戏性的融合

相比于将教育游戏的教育性和游戏性作为两个排他的因素进行平衡，本研究旨在推动教育性和游戏性的融合，从而实现两方面的交互发展。理论研究与需求分析为教育游戏设计开发提供了理论基础和内容基础，指导游戏的内容设计和总体设计。教育游戏的设计开发应以目标知识的内容设计为基础，贴合教学内容设计开展游戏总体设计，促进学习者发现知识本身的乐趣，从而激发内部动机。本研究立足于游戏的内容设计，开展贴合学习内容的游戏总体设计，融合发展教育性与游戏性。

（三）研究不足与反思

由于时间限制，本研究设计的游戏并没有得到大范围的测试，尚未开展后续教学工作;另外，游戏内容和规则还需要结合学生学习情况进行适应性的修改。因此，本研究设计的折叠与展开游戏还需要进一步的迭代优化和改进，如在游戏设计上，可以丰富游戏规则，探索渐进性玩法，以增强游戏趣味性;在内容设计上，可以利用游戏后台数据对学习内容的理论分析进行补充和完善，提升内容设计的科学性和有效性。在未来研究中，研究者可以通过迭代的优化以实现螺旋上升的游戲设计，最终落实到一线教育教学实践，进一步助力学生数学学习和空间能力的培养。

致谢：在研究过程中，感谢北京市顺义区西辛小学朱秋庭校长、刘学红校长、李云龙主任、付秀芳老师、张丽丽老师、赵海平老师、赵丽老师提供的指导、支持和帮助;感谢北京市顺义教育研究考试中心教研员周爱东老师、深圳市福田区教育科学研究院小学数学教研员姚铁龙老师提供的建议和指导;此外，还要感谢胡若楠、夏琪、石长征、张媛媛等北京大学学习科学实验室的老师、同学们给予的支持和帮助！

[参考文献]

[1] 傅孟霞.培养儿童空间认知能力的数字化游戏设计[D].济南：山东师范大学，2013.

[2] WAI J， LUBINSKI D， BENBOW C P. Spatial ability for STEM domains： aligning over 50 years of cumulative psychological knowledge solidifies its importance[J]. Journal of educational psychology， 2009， 101（4）：817-835.

[3] TOSTO M G， HANSCOMBE K B， HAWORTH C M A， DAVIS O S P， PETRILL S A， DALE P S， MALYKH S， PLOMIN R， KOVAS Y. Why do spatial abilities predict mathematical performance？[J]. Developmental science， 2014， 17（3）： 462-470.

[4] TURGUT M. Development of the spatial ability self-report scale（SASRS）： reliability and validity studies[J]. Quality & quantity， 2015， 49（5）：1997-2014.

[5] GUNDERSON E A， RAMIREZ G， BEILOCK S L， LEVINE S C. The relation between spatial skill and early number knowledge： the role of the linear number line[J]. Developmental psychology， 2011， 48（5）：1229-1241.

[6] MIX K S， CHENG Y L. The relation between space and math： developmental and educational implications[J]. Advances in child development and behavior， 2012， 42：197-243.

[7] HUBBARD E M， PIAZZA M， PINEL P ， DEHAENE S. Interactions between number and space in parietal cortex[J]. Nature reviews neuroscience， 2005， 6（6）：435-448.

[8] BUETI D， WALSH V. The parietal cortex and the representation of time， space， number and other magnitudes[J]. Philosophical transactions of the royal society b-biological sciences， 2009， 364（1525）： 1831-1840.

[9] UTTAL D H， MEADOW N G， TIPTON E， HAND LL， ALDEN AR， WARREN C， NEWCOMBE NS. The malleability of spatial skills： a meta-analysis of training studies[J]. Psychological bulletin， 2013， 139（2）：352-402.

[10] 曾嘉灵. 基于学习科学视角的数学空间能力教育游戏设计与应用研究——以小学五年级“立体图形的折叠与展开”为例[D].北京：北京大学，2020.

[11] 高晓旭.小学生几何图形折叠与展开困难的原因分析与对策研究[D].济南：山东师范大学，2018.

[12] 尚俊杰，张露.基于认知神经科学的游戏化学习研究综述[J].电化教育研究，2017，38（2）：104-111.

[13] GAGNON D. Videogames and spatial skills： an exploratory study[J]. Educational communication and technology journal， 1985， 33（4）： 263-275.

[14] FENG J， SPENCE L， PRATT J. Playing an action video game reduces gender differences in spatial cognition[J]. Psychological science， 2010， 18（10）：850-855.

[15] BOOT W R， KRAMER A F， SIMONS D J， FABIANI M， GRATTON G. The effects of video game playing on attention， memory， and executive control[J]. Acta psychologica， 2008， 129（3）：387-398.

[16] 田志明，朱小平.我們该教给学生什么？——对正方体展开图的深入研讨[J].小学教学参考：数学版，2010（3）：13-14.

[17] 钱建兵.有感于正方体展开图的“另类”教学[J].小学数学教育， 2016（20）：48.

[18] 何忠云.关注"三量"，提质增效——小学高年级数学课堂教学有效性策略探究[J]. 内蒙古教育，2015（8）：70.

[19] 张少刚.合理操作 发展想象——“长方体和正方体的展开图”教学片断与思考[J].小学数学教育，2017（20）：59-60.

[20] 袁红健.三问，在实践中发展空间观念——以“长方体和正方体表面的展开图”两次教学为例谈对比思考[J].数学教学通讯，2017（31）：31-33.

[21] 丁伟， 李一鸣.“展开与折叠”教学实录与评析[J].小学数学教育， 2018（Z1）：50-53.

[22] VOYER D， VOYER S， BRYDEN M P. Magnitude of sex differences in spatial abilities： a meta-analysis and consideration of critical variables[J]. Psychological bulletin， 1995， 117（2）：250-270.

[23] TVERSKY B. Structures of mental spaces —how people think about space[J]. Environment and behavior， 2003， 35（1）：66-80.

[24] FRANKLIN N， TVERSKY B. Searching imagined environments[J]. Journal of experimental psychology- general， 1990， 119（1）： 63.

[25] BRYANT D J， TVERSKY B， FRANKLIN N. Internal and external spatial frameworks for representing described scenes[J]. Journal of memory and language， 1992， 31（1）：74-98.

[26] NEWCOMBE N， HUTTENLOCHER J. Children's early ability to solve perspective-taking problems[J]. Developmental psychology， 1992， 28（4）：635-643.

[27] MA'RIFATIN S， AMIN S M， SISWONO T Y E. Students' mathematical ability and spatial reasoning in solving geometric problem[J]. Journal of physics conference series， 2019， 1157（4）：042062.

[28] SHEPARD R N， FENG C. A chronometric study of mental paper folding[J]. Cognitive psychology， 1972， 3（2）：228-243.

[29] ROBERTS J E， BELL M A. Two- and three-dimensional mental rotation tasks lead to different parietal laterality for men and women[J]. International journal of psychophysiology， 2003， 50（3）：235-246.

[30] FAW P J. A study of the development of the ability of selected students to visualize the rotation and development of surfaces[J]. Quality of life research， 1977， 6（6）：531-554.

[31] LIU A S， SCHUNN C D. The central questions of spatial cognition[J]. The oxford handbook of cognitive science， 2017，169：190.

[32] ARICI S， ASLAN-TUTAK F. The effect of origami-based instruction on spatial visualization， geometry achievement， and geometric reasoning[J]. International journal of science and mathematics education， 2015， 13（1）：179-200.

[33] YUN R， XI H， LI Y. The experiment of improving students' spatial ability by using VGLS[J].Advances in artificial reality and tele-existence， 2006，467-473.

[34] GOLDSTONE R L， LANDY D H， JI Y S. The education of perception[J]. Topics in cognitive science， 2010， 2（2）：265-284.

[35] VITALE J， BLACK J， SWART M. Promoting development of geometry concepts： interfacing multiple embodied representations with a computer game[J]. In Proceedings of the Annual Meeting of the Cognitive Science Society， 2011（33）： 33.

[36] BLACK J B， KHAN S A， HUANG S C D. Video and computer games as grounding experiences for learning[J]. Learning by playing： video gaming in education， 2014， 290-301.

[37] MILIVOJEVIC B，JOHNSON B W，HAMM J P，CORBALLIS M C. Non-identical neural mechanisms for two types of mental transformation： event-related potentials during mental rotation and mental paper folding[J]. Neuropsychologia，2003，41（10）：1345-1356.

[38] JAU？譒OVEC N， JAU？譒OVEC K. Sex differences in mental rotation and cortical activation patterns： can training change them？[J] Intelligence， 2012， 40（2）： 151-162.

[39] GLASS L， KRUEGER F， SOLOMON J， RAYMONT V， GRAFMAN J. Mental paper folding performance following penetrating traumatic brain injury in combat veterans： a lesion mapping study[J]. Cerebral cortex， 2012， 23（7）：1663-1672.

[40] DAN A， REINER M. Reduced mental load in learning a motor visual task with virtual 3D method[J]. Journal of computer assisted learning， 2017， 34（1）：84-93.

[41] MAYER R E. Applying the science of learning to multimedia instruction[J]. Psychology of learning and motivation： cognition in education， 2011， 55：77-108.

[42] MAYER R E. Computer games for learning： an evidence-based approach[M]. Cambridge： MIT Press， 2014.

[43] ANNETTA L A. The "I's" have it： a framework for serious educational game design[J]. Review of general psychology， 2010， 14（2）：105-112.

[44] CSIKSZENTMIHALYI M. Beyond boredom and anxiety. The experience of play in work and games[J]. Journal of individual psychology， 1977， 33（2）：267-268.

[45] ANNETTA L， MANGRUM J， HOLMES S，COLLAZO K， CHENG M T. Bridging realty to virtual reality： investigating gender effect and student engagement on learning through video game play in an elementary school classroom[J]. International journal of science education， 2009， 31（8）：1091-1113.

[46] FINNERAN C M. Flow in computer-mediated environments： promises and challenges[J]. Social science electronic publishing， 2013， 15（1）：82-101.

[47] PILKE E M. Flow experiences in information technology use[J]. International journal of human-computer studies，2004，61（3）：347-357.

[48] 馬颖峰，隋志华.基于Flow理论的教育游戏沉浸性设计策略研究——教育游戏活动难度动态调控研究[J].电化教育研究，2010，（3）：54-57，62.

[49] KOLB D A. Experiential learning： experience as the source of learning and development（Second Edition）[M]. NJ：Pearson FT Press， 2014.

[50] 张露，尚俊杰.基于学习体验视角的游戏化学习理论研究[J].电化教育研究，2018，39（6）：11-20，26.

[51] EKSTROM R B， FRENCH J W， HARMAN H H. Manual for kit of factor-referenced cognitive tests[M]. Princeton， NJ： Educational Testing Services，1976.

[52] 吴明隆，涂金堂. SPSS与统计应用分析[M].大连：东北财经大学出版社，2012.

Research on Design and Application of Mathematical Spatial Games from Learning Sciences Perspective

SHANG Junjie，  ZENG Jialing，  ZHOU Junyi

（Lab of Learning Sciences， Graduate School of Education， Peking University， Beijing 100871）

[Abstract] Spatial ability is one of the keys to talent training in the information age and is closely linked to mathematics learning. However， it is found that folding and unfolding of three-dimensional figures is an important and difficult point in the teaching of graphics and geometry in Chinese elementary school. Educational game environments can promote the development of mathematical cognition and spatial ability. As a result， this study adopts the design-based research method， based on the relevant research results of pedagogy， psychology， and cognitive neuroscience research on folding and unfolding from the perspective of learning sciences， analyzes the theories related to educational games to construct the three-dimensional game design principles of cognition， motivation and regulation， and designs and develops a folding and unfolding educational game "Cube Elimination". An applied study is also conducted to evaluate the actual effect of the game. The study analyzes the performance data of 32 students and finds that the students' mathematical knowledge learning and mental folding abilities have been improved significantly after a 40-minute daily game-based instructional intervention for a total of three days， especially for students with lower initial knowledge proficiency.

[Keywords] Learning Sciences; Educational Games; Gamified Learning; Mathematical Cognition; Graphics and Geometry; Spatial Ability; Folding and Unfolding; Mental Folding

[作者简介] 尚俊杰（1972—），男，河南林州人。研究员，主要从事学习科学与技术设计、游戏化学习、教育技术领导政策等研究。E-mail：jjshang@pku.edu.cn。

基金项目：北京市教育科学“十四五”规划2021年度延续课题“基于学习科学和游戏化学习的学习能力培养研究"（课题编号： CEFA21067）