灵活应用所学知识解决问题
2022-05-30王岚
王岚

学习知识一定要活学活用,学习数学亦是如此,切记不能生搬硬套、墨守成规.“看菜吃饭,量体裁衣”,说的也是这个道理.我们一定要根据实际情况灵活应用所学知识解决问题.
例1 甲、乙两人分别在六次射击中的成绩(单位:环)如右表所示:你知道在六次射击中成绩发挥比较稳定的是哪一位吗?
思路点拨:看过此题就知道是要比较稳定性,有的同学立刻联想到老师讲过的规律,“方差越小,数据的波动就越小,该组数据就越稳定;方差越大,数据的波动就越大,该组数据就越不稳定”,从而得出结论.这种做法有点墨守成规,计算起来比较麻烦.仔细观察两组数据就会发现:甲组数据的极差是:8 - 6 = 2,乙组数据的极差是:9 - 5 = 4,且甲组数据中有3对相同的数据,乙组数据中仅有2对相同的数据. 另外甲组数据中有2个数等于平均数7,而乙组数据中没有等于平均数的数据. 据此断定甲组数据波动小,也就是说甲組数据稳定,根本没有必要计算方差.
例2 如图1,?ABCD中,对角线AC,BD相交于点O,过点O分别作OE⊥AD于E,OF⊥BC于F. 求证:OE = OF.
马小虎同学不假思索地做出如下证明:
∵四边形ABCD是平行四边形,∴OA = OC.
∵OE⊥AD,OF⊥BC,∴∠AEO = ∠CFO = 90°.
∵∠1 = ∠2,∴△AOE≌△COF(AAS),∴OE = OF.
这种证法看似天衣无缝,其实却有漏洞.通过证明△AOE与△COF全等,然后利用“全等三角形的对应边相等”来证明OE = OF,这个证明思路没有问题. 不过为什么会有“∠1 = ∠2”呢?他竟理直气壮地回答:“∠1与∠2是对顶角,当然相等.” ∠1与∠2真是对顶角吗?假如∠1与∠2是对顶角,那么点E,O,F三点应该在一条直线上.可是从已知条件中无法得出这个结论. 俗话说,“条条大道通罗马”. 由于证明E,O,F三点共线既困难又麻烦,因此我们可以绕过这个“关卡”,避免证明E,O,F三点共线. 下面提供三种思路.
思路点拨:方法一:从证明∠EAO = ∠FCO入手,证明△AOE≌△COF.
方法二:由OE,OF分别是△AOD与△BOC的高,联想“全等三角形对应边上的高相等”,可以考虑证明△AOD≌△COB.
方法三:由高联想面积,要证OE = OF,由于AD = BC,可以考虑证明△AOD与△BOC的面积相等.
由此看来,解决数学问题时,不要“钻牛角尖”,要注意“避其锋芒”,换一个角度,曲径通幽,会达到“柳暗花明”的境界.
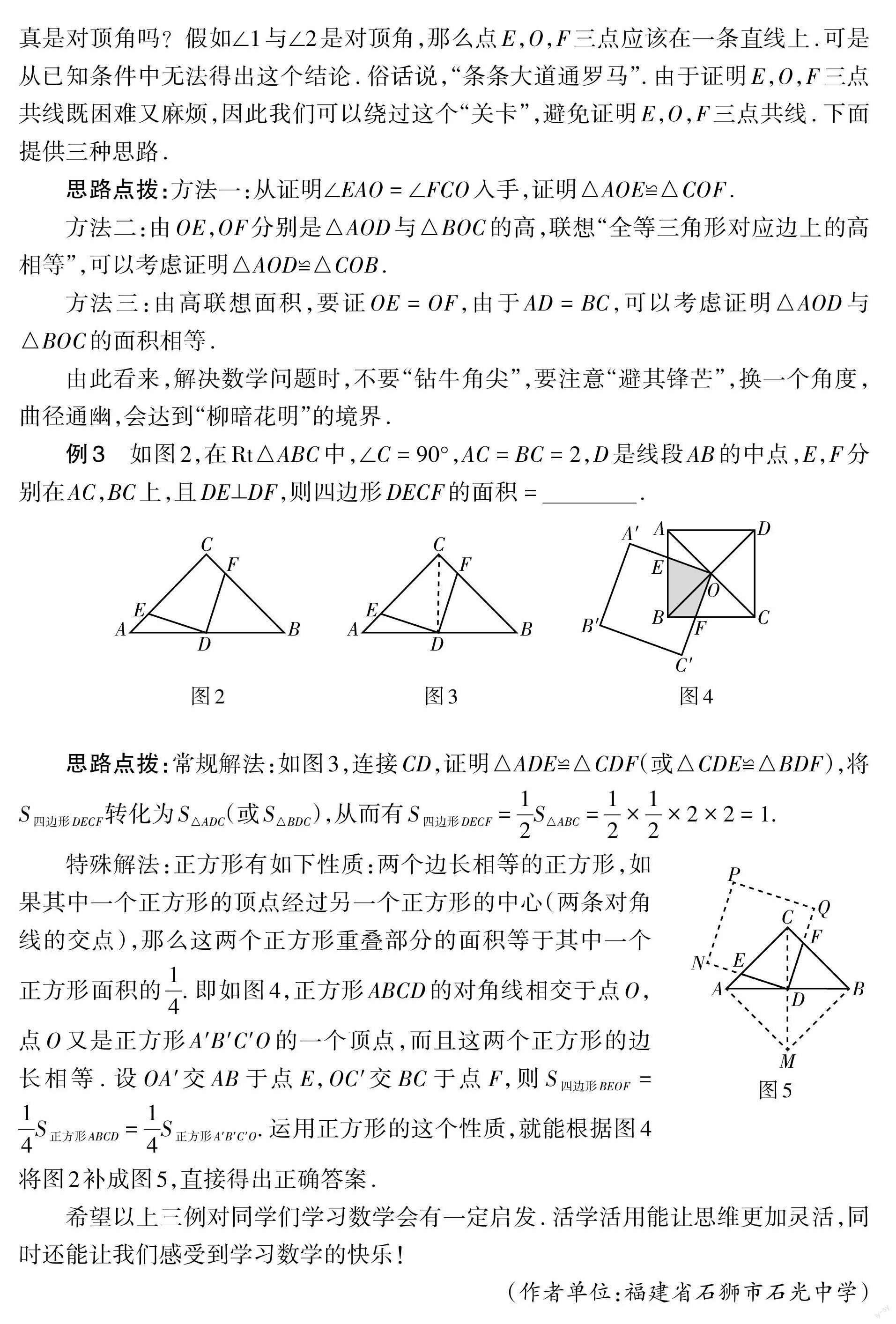
例3 如图2,在Rt△ABC中,∠C = 90°,AC = BC = 2,D是线段AB的中点,E,F分别在AC,BC上,且DE⊥DF,则四边形DECF的面积 = .
思路点拨:常规解法:如图3,连接CD,证明△ADE≌△CDF(或△CDE≌△BDF),将S四边形DECF转化为S△ADC(或S△BDC),从而有S四边形DECF = [12]S△ABC = [12] × [12] × 2 × 2 = 1.
特殊解法:正方形有如下性质:两个边长相等的正方形,如果其中一个正方形的顶点经过另一个正方形的中心(两条对角线的交点),那么这两个正方形重叠部分的面积等于其中一个正方形面积的[14]. 即如图4,正方形ABCD的对角线相交于点O,点O又是正方形A'B'C'O的一个顶点,而且这两个正方形的边长相等. 设OA'交AB于点E,OC'交BC于点F,则S四边形BEOF = [14]S正方形ABCD = [14]S正方形A'B'C'O. 运用正方形的这个性质,就能根据图4将图2补成图5,直接得出正确答案.
希望以上三例对同学们学习数学会有一定启发. 活学活用能让思维更加灵活,同时还能让我们感受到学习数学的快乐!
(作者单位:福建省石狮市石光中学)
