学习难点,教学整合的出发点
2022-05-30余庆玲
余庆玲

【摘 要】在根据学生学习难点找准教学着力点的基础上,教师对北师大版教材四年级上册“角的认识”相关内容进行教学整合。整合后,教师将《相交与垂直》《旋转与角》2课时内容合并成1课时教学。教学实践表明,整合后的教学有助于学生更好地理解相交、垂直、角等概念,建立结构化的知识体系。
【关键词】教学整合;角的认识;整体建构
“学生立场、单元视角、有机整合、适度拓展”是实现“生本课堂”提高教师专业水平的有效途径。教学中,教师需要理清教学内容的知识脉络及前后联系,透析数学本质,根据学生的学习难点找准教学的着力点,并据此进行教学或内容重构,帮助学生建立有结构的知识体系。按照结构化的思路教学时,可联结单元内或单元间的内容,提升教学的系统性,以使学生的数学学习更有张力和厚度。下面以北师大版教材四年级上册“角的认识”相关内容为例,谈谈如何根据学生的学习难点实施单元教学整合。
【教学思考】
一、学习内容分析
“角的认识”是平面几何教学中的重要内容。教学前教师自己先要清晰地理解角的概念。在平面几何中,角有静态与动态两种基本定义。角的静态定义为:具有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的两条边。角的动态定义为:一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角,所旋转射线的端点叫做角的顶点,开始位置的射线叫做角的始边,终止位置的射线叫做角的终边。
理解了角的定义后,可以发现在本单元教学内容中的“相交与垂直、旋转与角”之间存在着一些隐性的“逻辑关系”。 平行和相交表示的都是两条直线的位置关系。可以想象,一条直线在平面上运动,其基本运动方式有平移和旋转两种。一条直线平移后,运动的起始位置与终止位置的两条线相互平行。如果在直线上任取一个点,直线绕着这个点旋转,那么直线的起始位置与终止位置的两条线相交,线相交自然会形成角。
二、学习难点分析
在北师大版教材中,角的学习内容包括“认识角、角的分类、角的度量”三大板块,其中有关“认识角”的内容,教材分别在二年级下册安排了《认识角》,在四年级上册安排了《旋转与角》两课,从静态定义和动态定义两个层面,引导学生进行角的初步认识和再认识。
在二年级下册教学《认识角》时,学生要借助具体的事物来认识角。因为从生活中找到的角往往都具有“形”的特质,所以在学生的心目中就容易产生“能看到的边越长角越大”的错觉。如图1中,学生常会觉得“鳄鱼嘴巴的开口比人的嘴巴开口大”,理由是鳄鱼嘴巴能装进去的东西比人嘴巴能装进去的东西多。可见学生容易把“容纳的大小、开口的间距”错当角的大小。
三、解决难点的路径
为突破“角的大小与画出的边长短无关,只跟两条边张口的大小有关”这一教学难点,笔者尝试通过“让角的概念跟旋转相连,建立两条边的位置关系”的方式重构教学内容。
在二年级教学《角的初步认识》时,教师应尽量选择与旋转相关的物体作为教学素材,让学生感受因旋转所产生的位置关系,与角的形成有密切关系。教学四年级“线与角”单元时,教师把“相交与垂直”“旋转与角”整合为一课时,让学生通过“旋转”理解“相交、角、垂直”三个概念,并感悟它们之间的联系。通过角的动态形成过程,赋予“始边”和“终边”的概念,再在比较不同大小的角的过程中,明确“角的大小与画的边长短无关,只跟两条边张口的大小有关”。
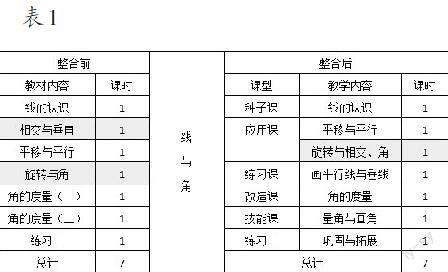
整合后的教学路径为:在直线上任取一点,直线绕着这个点旋转,直线的起始位置与终止位置是一种相交的关系,相交后的图形上有角;将一条射线绕其端点进行旋转,其起始位置与终止位置形成了角。旋转的张口越大,形成的这个角就越大,因此就形成了各种大小不同的角。整合后“线与角”单元的教学顺序调整为表1。
【教学实践过程】
根据以上分析确定本内容教学目标为:(1)通过旋转认识相交、角、垂直与垂线等概念,明确各类角之间的大小关系,感受知识的生长性和整体性。(2)能正确判断两条直线是否相交,能准确辨认各类角,并能按要求画出已知直线的垂线。
一、复习图形的运动方式
教师在黑板上画一条直直的线。
师:黑板上有一条直直的线,如果它在黑板上运动,可以有哪些不同的运动方式?
生:平移和旋转。
师:如果做平移运动,它运动前所在的位置我们称之为“起始位置”,运动后停留的位置我们称之为“终止位置”。想象一下,它的起始位置与终止位置所在的两条直线之间有怎样的位置关系?
生:平移后,它的起始位置与终止位置所在的直线是一组平行线。
师:如果做旋转运动,运动前的直线和运动后的直线又会产生怎样的位置关系呢?
师:今天我们就研究研究。
二、体会旋转与相交、旋转与角的关系
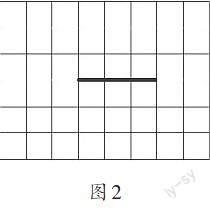
教师提供操作板(自制学具)。出示图2,图中有一根可旋转的磁棒,并描出这根磁棒的起始位置。
师:请每位同学在操作板上用自己喜欢的方式将这根磁棒进行旋转,并画出磁棒的起始位置与终止位置。
(学生动手操作,教师巡视收集、呈现两种不同旋转情况的學生作品)
师:说说刚才你是怎么进行旋转的?
生:我是绕磁棒上的一个点进行旋转的。(边比画边说明,如图3)
师:此时你是把这根磁棒看作一条什么线绕一点旋转的?
生:直线。
师:有跟他不一样的旋转吗?
生:我是绕磁棒的一个端点旋转的。(边比画边说明,如图4)
师:此时你又是把这根磁棒看作一条什么线绕一点旋转的?
生:射线。
师:两位同学磁棒的旋转有什么共同的地方。
生:都会得到角。
小结:将小棒绕小棒上一点旋转,起始位置与终止位置所在的直线可以形成角;将小棒绕其端点旋转,起始位置与终止位置也形成了一个角。
三、了解角的属性与类别
教师呈现“绕着磁棒的端点旋转”的学生作品。
师:接下来,我们重点研究一条射线绕它的端点旋转而形成角的情况。
师:这么多的角相互间有什么区别吗?
生:它们的位置不同。
生:角的大小不同。
师:你所说的角的大小指的是什么?
生:两条射线之间的张口大小就是角的大小。
师:在这些旋转而成的角中,你觉得哪个角最特别?特别在哪里?
师:根据两条边相交的位置关系,可以把角分为锐角、直角、钝角、平角、周角。
师:结合前面的学习经历,说说“关于角,你有了哪些体会?”
小结:角是一条射线绕着它的端点旋转而成的,两条射线的交点就是角的顶点,射线的起始位置是角的始边,射线的终止位置是角的终边。旋转的幅度越大,形成的角越大。角的大小和旋转幅度有关,和边画的长短无关。
四、认识垂直与垂线
教师介绍:当两条直线相交成直角时,我们就说这两条直线互相垂直,其中一条是另一条的垂线,它们的交点叫垂足。
学生操作:过直线上一点和直线外一点分别作已知直线的垂线。
学生反馈并交流作图方法。
五、巩固练习(略)
【教学反思】
将“相交与垂直、旋转与角”整合,引导学生从旋转的角度认识角,学生会更容易理解无论射线怎么延伸,其位置关系不会改变。“角的大小”这一教学难点不攻自破。
“相交与垂直、旋转与角”整合后,为学生后继量角与画角的学习积累了活动经验,有助于实现前后知识的相通和学习的迁移,体现知识的生长性和系统性。
单元整合是课程与教学之间的桥梁,是教师对课程的二度开发,是让教学更有系统性、时效性的有效策略和途径。教學整合,要真正做到从学生的需要出发,在找准学生学习难点后进行整体教学设计,帮助学生感悟知识本质,发展思维能力。
(浙江省金华师范学校附属小学 321000)
