大概念引领下的数学原理课教学探究
2022-05-30刘铁智吕增锋
刘铁智 吕增锋

【摘 要】从知识点教学走向学科大概念教学是解决数学原理课“没什么好教”的有效途径。大概念引领下的数学原理课教学策略是:首先,立足“是什么”的大概念,解读数学原理的育人功能;其次,立足“如何学”的大概念,构建宏大的数学原理学习场景;最后,立足“学得怎么样”的大概念,在迁移应用中获得数学原理。
【关键词】大概念;计数原理;数学原理教学;数学育人
根据教学内容把数学课堂教学进行分类,一般可以分为概念课、习题课、公式课、定理课、原理课等课型。相对于其他课型,纯粹的数学原理课比较少,在高中数学中只有两个基本计数原理、立体几何的三个基本事实、充要条件等。此外,数学原理课内容往往比较简单,就拿两个基本计数原理来说,就是小学阶段加法运算与乘法运算的简单推广,学生在理解上不会有太大难度,这也无形中让教师产生“没什么好教”的错觉。因此,在数学原理课教学中,原理建构通常都被一带而过,很多教师都把重心放在原理的应用上,通过大量的例题与习题进行巩固提升,硬生生地把原理课上成了习题课,数学原理课应有的育人功能无法得到充分发挥。因此,笔者建议教师应从数学育人的角度重新审视数学原理课的教学策略。
一、大概念及大概念教学的内涵
大概念指的是反映专家思维方式的概念、观念或论题,它具有生活价值[1],是居于学科基本结构的核心概念或若干居于课程核心位置的抽象概念整合相关知识、原理、技能、活动等课程内容要素,形成有关联的课程内容组块[2]。大概念的“大”不是指“庞大”,因此,不能以所包含的知识范围的大小来判断一个概念是否是大概念。这里的“大”指的是“核心”“高位”或“上位”,即学科领域中最精华、最有价值的核心内容,是力图对学生的认知基础进行集成与融合的概念,具有较强的迁移价值。比如,函数是刻画客观世界变化规律的重要模型;平面向量是沟通代数、三角、几何的桥梁;解析几何的核心是用代数方法解决几何问题;等等。这些都可以称为数学中的大概念。大概念能够解释较大范围内的一系列相关现象、事实以及相互关系;能将较大范围内分散的知识和事实联结为有结构、有系统的整体;能作为一种解释模型,赋予个别的、具体的事实以深层的意义。按照大概念的教学功能来分,可以被分为指向“学什么”“如何学”“学得怎么样”的大概念。当然这些指向有的是明指,有的是暗指,比如,几何学是认识现实世界的基石明指几何学是基石,暗指几何学在数学中的基石作用;又比如,用空间角来刻画垂直关系明指空间角的重要作用,暗指证明垂直需要找到相应的空间角。
大概念教学则是以大概念为锚点组织教学的一种方式,其一般操作步骤如下。首先,用大概念统摄与组织教学内容,能够使离散的事实、技能相互联系、结构化,并被赋予一定意义。其次,大概念教学强调引导学生超越对知识和技能的学习,走向那些超越时空和情境所存在的、可迁移的观点和思想[3],从而促使深度学习的发生。最后,大概念教学有明晰的学习目标,有效的表现性任务,有利于学生自主、合作、探究学习,完成学习成果。在大概念教学中,教师要成为学科教学的专家,不仅要知道教什么,还要知道为什么而教;不仅要理解学生,也要理解设计,包括单元设计、活动设计、问题设计等,用自己丰富的专业知识引领学生像专家那样思考,使学生也成为学习的专家。大概念教学结构、联系、迁移的基本特征,使其可以直指数学原理的中枢,不仅可以让学生更好地理解数学原理,而且有助于在原理教学中实现由知识教学向素养培育的跨越。下面笔者以“两个基本计数原理”为例,谈谈大概念引领下的数学原理课教学。
二、大概念引领下的数学原理课教学
(一)立足“是什么”的大概念,解读数学原理的育人功能
众所周知,对教学内容的解读是教学设计的基础,解读是否到位,不仅关系到能否真正发挥教材的作用,还会直接影响到课堂教学的质量。不同于一般的教学内容,数学原理往往具有内容的基础性和运用的无意识性并存的特点,即数学原理本身简单,学生平时也在运用,但这种运用是一种无意识的运用,学生不会把这种运用上升到数学原理的高度去理解。因此,在对数学原理的解读中,不要局限于对零碎知识点的剖析,而是要立足“是什么”的大概念的前提下,在关注“四基”“四能”的同时,着重分析其潜在的育人功能,以育人功能来统领知识与方法,从而唤醒学生主动提炼数学原理、运用数学原理的意识。
常用的指向“是什么”的大概念有“数学是模型”“数学是工具”“数学是运算”“数学是推理”等。“两个基本计数原理”是为“计数”服务的,分类计数原理解决问题是将一个复杂问题分解为若干类别,然后分类解决,各个击破;分步计数原理是将一个复杂问题的解决过程分解为若干步骤,先对每个步骤进行细致分析,再整合为一个完整的过程。由此,可以得到计数原理“是什么”的大概念,即计数原理是实现科学计数的方法与策略。于是,在这个大概念的引领下再对教学内容进行解读的话,本节课的核心内容及育人功能就很清晰,即“一个中心”“两个原理”“三个关键”“四个素养”,如图1,其中“四个素养”指的是育人功能。
围绕“是什么”的大概念来进行教学分析,不仅可以明确数学原理的本质,而且还能解决数学原理解读中存在的逻辑混乱、顾此失彼、视角单一等一系列问题,从而实现教学分析完整化、系统化。
(二)立足“如何学”的大概念,构建宏大的数学原理学习场景
不可否认,数学原理本身往往比较简单,内容也比较单薄,但这并不意味着数学原理的教学就可以不用遵循意义建构的方法与原则,其教学过程就可以简化为教师呈现原理,学生记忆原理与运用原理。事实上,数学原理的形成都需要经历从具体到抽象的过程,要让学生真正了解原理的来龙去脉,必须要依托数学大概念,因为数学大概念本身就是对课程标准、核心素养、教学重难点、评价标准等深度提炼的结果,其所展现出来的“如何学”的内涵可以有效调动学生学习的内在驱动力。
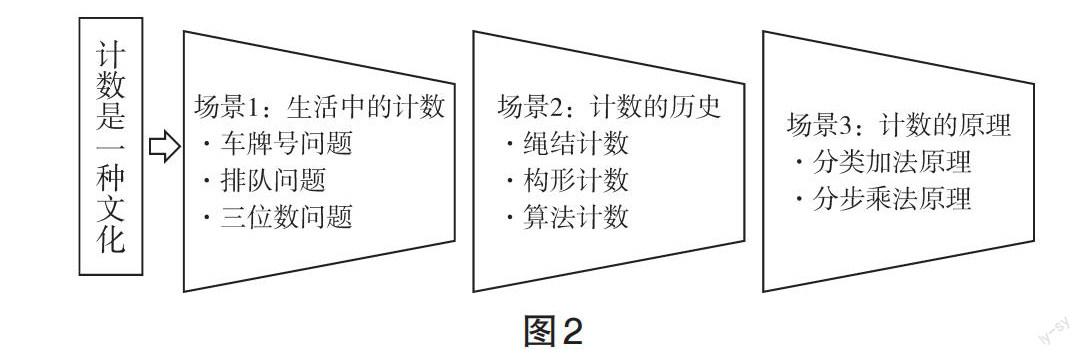
常用的指向“如何學”的大概念有“数学重在理解”“用联系的观点看数学”“数学要关注应用”“数学要凸显文化价值”等。计数问题不仅与生活息息相关,而且历史悠久。早在数字出现之前,古人就开始结绳计数,其原理是把绳结与要计数的对象对应起来,体现了数学的映射思想;随着数字的发明,古希腊的数学家开始构形计数,用鹅卵石把数字按照一定形状排列出来,就形成了所谓的形数,比如三角形数、四边形数、五边形数等,再通过图形的几何特征来计数,我国古代的垛积数采用的也是相同的方法;随着运算的发展就进入了算法计数的时代,各种算法的出现加快了计数的效率。由此可见,尽管两个基本计数原理只是加法运算与乘法运算的推广,但其背后蕴含着丰富的数学文化。因此,计数是一种文化应该成为如何学习本节内容的大概念。在这个大概念的引领下,就可以构建生成“两个基本计数原理”的三大学习场景,即生活中的计数、计数的历史、计数的原理(如图2所示),从而使本节课的学习成为一场数学文化的盛宴。
在“生活中的计数”场景中,教师可以设计以下问题引发学生对于生活中“计数”需求的思考。
问题1-1 我国民用汽车号牌的编号由两部分组成。第一部分为用汉字表示的省、自治区、直辖市简称和用英文字表示的发牌机关代号。第二部分为由阿拉伯数字和英文字母组成的序号,其中,序号的编码规则为:
(1)由10个阿拉伯数字和除0之外的24个英文字母组成;
(2)最多只能有2个英文字母。
如果某地级市发牌机关采用5位序号编码,那么这个发牌机关最多能发放多少张汽车号牌?
问题1-2 某运动会上,8名男运动员参加100米决赛,其中甲、乙、丙三人必须在1,2,3,4,5,6,7,8八条跑道的奇数号跑道上,则安排这8名运动员比赛的方式共有 种。
问题1-3 用0,1,2,3,4五个数字,
(1)可以排成多少个三位数字的电话号码?
(2)可以排成多少个三位数?
(3)可以排成多少个能被2整除的无重复数字的三位数?
问题1-4 如果数量很少,可以一个一个的数;如果数量很多,还能一个一个地去数吗?
在“计数的历史”场景中,通过介绍绳结计数、构形计数、算法计数三种计数方法来呈现计数的历史脉络。其中,绳结计数是人类最原始、最简单的计数方法,对应的计数原理就是逐个数,特点是操作简单,但效率低;构形计数指的是通过把数字按照一定的规律排列成几何图形,再利用图形的性质进行计数,古希腊的“形数”和我国古代的“垛积术”均属于这类计数的范畴,其特点是化数为形,巧妙构造;算法计数借助比较成熟的运算法则与技巧进行计数,程序化、高效化是其最显著的优点,尤其进入信息时代,算法计数成为发展趋势,而本节课的两个原理正是算法计数的理论基础。
在“计数的原理”场景中,让学生经历原理的形成、原理的比较、原理的推广、原理的应用的完整过程,在丰富的生活情境中,逐步领会分类标准不重不漏、分步标准步骤完整的计数精髓。
(三)立足“学得怎么样”的大概念,在迁移应用中获得数学原理
数学原理往往是在运用中被感知与发现的,两个计数原理其实就是人们在解决计数问题中的经验与方法的总结,而且迁移应用也是衡量“理解”的一个重要指标,即把所学的知识迁移到新的环境和挑战中,而不仅仅是知识的回忆和再现。深入的理解是获得数学原理的前提,为了加速这个过程,教师应围绕“学得怎么样”大概念设计相关的启发性问题,比如,“是否可以利用大概念来解释问题”“是否需要对大概念做进一步完善”“能否运用大概念进行创造性活动”等[4],从而使学生在经历从具体到抽象的归纳,再从抽象到具体的演绎过程中实现对数学原理的自然建构。
常用的指向“学得怎么样”的大概念既包括“四基”“四能”“三会”,还包括学习数学所具备的思维品质,比如,敢于质疑、善于思考、实事求是的精神。例如,为了区分两个计数原理的异同,可以围绕“三会”这个大概念设计形同质异的问题。
问题2-1 如果用一个大写的英文字母或一个阿拉伯数字来给座位编号,总共能编出多少种不同的号码?
问题2-2 某班级有男生30名,女生24名,现从中任选1名男生或女生代表班级参加比赛,共有多少种不同的选法?
问题3-1 如果要求座位编号是两位编码,第一位是英文字母,第二位是阿拉伯数字,共能编出多少种不同的座位编号?
问题3-2 某班级有男生30名,女生24名,现从中任选男生和女生各1名代表班级参加比赛,共有多少种不同的选法?
通过比较分析两组问题的“异”与“同”,不仅可以让学生体会到现实计数中“差之毫厘谬以千里”的客观事实,帮助学生树立仔细审题的意识,而且有助于揭示计数原理中“分类”“分步”两个本质属性。
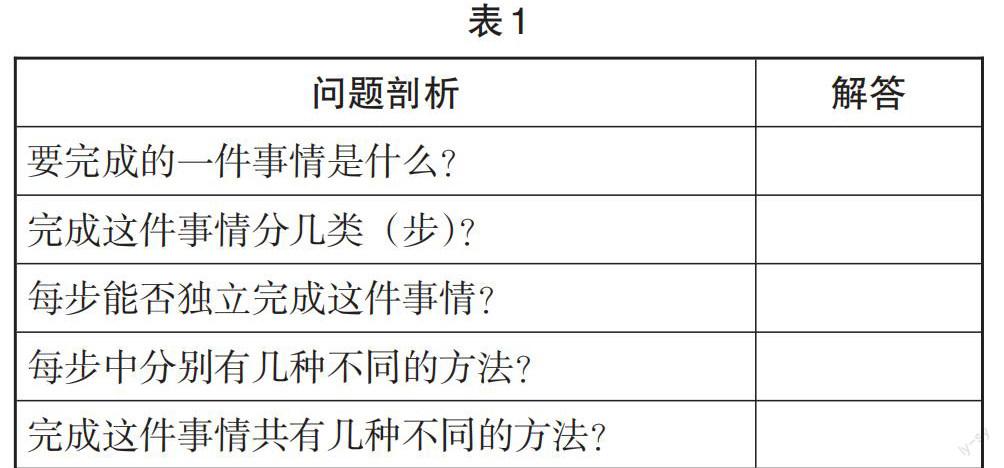
例如,为了构建原理应用的路径,教师可以围绕“四能”这个大概念设计能够引发学生思考的表格(见表1)。
计数原理指向的是解决问题的策略与方法,表1为计数提供了一般的路径,实现了计数问题的算法化,尤其是学生一开始对于计数问题不熟悉的时候,这张表格可以为学生提供思维指引,可以有效避免计数的重复与遗漏。
教学是一个复杂的系统工程,每个学期、每个单元、每节课既有各自目标,又相互影响、相互制约,它们之间构成一个有机整体。在教学设计时,教师须持有这种整体的理念来规划教学[5]。大概念引领下的数学原理教学,可以将数学原理的本身、原理育人的功能、原理的构建等都纳入数学教学的大系统中去考量,从而促使知识体系结构化、整体化,有助于发展学生的核心素养。
參考文献:
[1]刘徽.“大概念”视角下的单元整体教学构型:兼论素养导向的课堂变革[J].教育研究,2020(6):64-77.
[2]吕立杰.大概念课程设计的内涵与实施[J].教育研究,2020(10):53-61.
[3]刘徽.大概念教学:让教育新理念真正落地[J].上海教育,2020(11):1.
[4]何美婕,刘徽,蒋昕昀.大概念教学应用阶段的教学设计[J].上海教育,2020(11):58-60.
[5]邵朝友,韩文杰,张雨强.试论以大观念为中心的单元设计:基于两种单元设计思路的考察[J].全球教育展望,2019(6):74-83.
(责任编辑:陆顺演)
