科技金融资源配置效率区域差异研究

王永辉 邵林

选取2016—2020年31个省市区科技金融的相关数据，运用BCC模型和CCR模型对全国31个省市区科技金融资源配置效率进行评价。实证研究发现，我国科技金融资源配置效率存在区域差异。与此同时，还需要从科技金融产品创新和金融市场改进、政府科技金融与市场科技金融协同、科技金融参与主体多元化等方面进一步促进我国科技金融健康发展，提高自主科技创新能力。

一、引言

科学技术的发展对促进经济高质量发展，增强我国经济的竞争力起着重要作用。科技创新对推动我国经济优化升级、实现高质量发展具有重要作用。然而，科技创新从技术研发到成果转化再到生产环节这一系列流程都需要大量的资金支持，且由于科技创新的高风险性，需要建立从技术研发到生产环节的风险共担机制，需要多方金融主体的配合。科技金融是金融产业与科技产业的有机融合，它引导金融资本和资源向科技创新领域倾斜，优化科技金融资源配置，促进经济转型升级，促进经济竞争力，实现高质量发展发挥着至关重要的作用。科技金融资源配置效率反映了我国金融资源和科技资源配置的合理程度，金融资源和科技资源的结合对实现经济转型优化升级，建设创新型国家具有重要的支撑作用［1］。

二、文献回顾

关于科技金融定义的界定，目前学术界尚未形成共识。赵昌文等（2009）提出科技金融“工具论”，他认为科技金融是一种金融工具，是一种对推动科技活动和技术创新、加快授权专利转化以及促进科技企业发展具有关键作用的制度安排［2］。Haslem等（1999）搜集了美國1987—1992年商业银行的相关数据，运用数据包络分析（DEA）对银行的金融创新效率进行实证分析，研究发现有五分之一的商业银行存在金融创新效率偏低的问题，商业银行需要通过松弛改进，优化金融资源的投入和产出，提高金融服务效率和质量［3］。Abdullah Saeed等（2018）通过对阿曼地区金融市场与科技型企业的调查显示，阿曼金融体系的优化与金融机构的服务效率二者呈正相关的关系，金融体系的不断优化会带动科技型企业的发展并以此促进经济社会的发展［4］。

国内对科技金融效率的研究主要是从投入和产出角度构建科技金融效率评价体系。科技金融效率的评价方法可以分为参数统计法和非参数统计法。参数统计方法最具代表性的就是随机前沿分析法（SFA），而非参数统计法最常见的就是数据包络分析法（DEA）。甘星等（2017）运用数据包络分析法（DEA）对我国三大经济圈的科技金融效率进行分析，研究发现江苏、浙江、安徽、辽宁、河北和山东的科技金融效率小于1，未处于有效状态，并针对目前6省市科技金融发展存在的问题提出改进措施［5］。陶立祥等（2020）运用数据包络分析（DEA）通过搜集2013—2017年武汉市科技金融的相关数据建立科技金融评价指标体系，研究发现武汉市科技金融综合效率虽然没有处于有效状态，但处于上升阶段，且呈现规模递增状态［6］。杜金岷等（2016）运用随机前沿分析模型（SFA）对我国31个省市的科技金融效率进行分析，发现只有北京、上海等7个省市的科技金融效率处于有效状态。其他省市的科技金融综合效率都没有处于有效状态［7］。贺宝成等（2021）运用DEA-BBC模型对2008-2018年我国29个省市的科技金融数据进行分析，研究发现科技金融效率存在区域差异，仅北京、广东五个省市的科技金融效率均为有效状态，其余省份的科技金融效率均没有达到有效状态，有待进一步完善［8］。李天籽等（2022）结合Undesirable-SBM模型等模型对武汉城市圈2010—2019年面板数据进行分析，研究发现忽略科技创新过程中的风险会使科技金融效率虚高，武汉城市圈科技金融效率重心轨迹呈东北—西南的格局［9］。张清叶等（2022）利用DEA-Malmquist法构建科技金融效率评价体系，对河南省科技金融效率进行实证分析，研究发现河南省科技金融技术效率呈明显的上升趋势，而科技金融规模效率则恰恰相反，各地市之间科技金融效率区域差异加大，需要具体问题具体分析［10］。

国内外学者对科技金融效率进行了大量研究但仍存在着许多不足：第一是大半部分学者只是从静态上研究固定时点上各地区科技金融效率的差异，而从动态上分析科技金融资源配置效率的变化的文章少之又少；其次，在科技金融评价体系构建时，科技金融数据和指标的选取上不够合理，例如有学者将GDP增量作为科技金融产出的评价指标，但GDP的增加不仅跟科技金融有关，所以会对研究结果产生一定的偏差。本文通过运用DEA模型对2016-2020年我国31个省市的科技金融资源配置效率进行研究，希望能够全面、准确地反映5年间我国科技金融资源配置效率的真实发展情况，提出有益于我国科技金融发展的针对性建议，促进经济高质量发展。

三、研究方法、指标选取与数据说明

（一）研究方法

数据包络分析（DEA）是一种非参数统计方法，其工作原理简单，即将某一决策单位与另一决策单位进行比较，进而得出该决策单位的效率，即利用决策单元的输入、输出数据，对有效生产前沿面进行估算，再由各个决策单位之间的有效边界距离来判定各决策单位的有效性。CCR模型和BCC模型是DEA中最常用的模型［11］。

1.CCR模型。假设存在n个决策单元（DMU），每个决策单元（DMU）包含m种投入，分别记作xi（i=1，2，……，m），存在q种产出，分别记作yr（r=1，2，……，q），将选取的决策单元记为DMUk。将其带入CCR模型中，决策单元DMUk的效率值可以通过以下公式进行计算：

上述算式中，λj为决策单元的系数，s-为决策单元投入松弛变量，而s+为决策单元产出的松弛变量。在上述算式中，将决策单元的效率值记作θ*（0≤θ*≤1）。设ε设为一个无限趋近于0的正数，在进行实证分析时可将其设置为0.0000001。当决策单元的效率值θ*=1，并且s-和s+都等于0时，这时就认为决策单元DMUk处于强有效的状态；在最优解θ*=1时，如果决策单元的s-和s+不等于0，则判定 DMUk是一个弱有效的状态；如果最优解θ*<1时，判定 DMUk被视为无效状态。

2.BCC模型。通过CCR模式以计算出决策单元的综合效率，但不能判定纯技术效率与规模效率的大小。因此，为对决策单位的技术有效性进行分析，仅需将约束条件 ∑=1加至 CCR模型，即 BCC模型，其结果与被评估的决策单位具有同样的生产规模。BCC模型中，利用下列模型计算出决策单元 k的效率值：

（二）指标选取与数据说明

1.指标选取。构建科技金融资源配置效率评价体系时，指标的选取要科学、合理，能够全面的展现科技金融投入与产出的实际情况，同时确保相关科技金融数据的可得性和可靠性。遵循科学性和合理性等原则，本文选取的科技金融资源配置效率的相关指标如表1。

各指标的说明如下：

（1）规模以上工业企业R&D活动人员：反映企业参与科技研发人员的数量的指标，由R&D人员全时当量得到。

（2）规模以上工业企业R&D经费内部支出：反映企业研发经费投入力度，由基础研究经费、试验发展经费和应用研究经费构成。

（3）科技支出占一般公共预算支出的比重：反映政府对科技创新活动的支持力度，由政府科技支出占政府公共支出的比重来表示。

（4）专利申请授权量：反映科技创新活动活跃程度，由专利申请数和专利授权数得到。

（5）规模以上工业企业新产品销售收入：反映企业在生产经营活动中创新产品所取得的销售收入［12］。

2.數据说明。选取2016—2020年全国31个省市科技金融的相关数据，数据来源于《高新技术产业统计年鉴》《中国统计年鉴》和Wind数据库。由于数据的可得性，对缺失相关年份和省市的数据采用ARIMA填补。

四、实证研究

运行Deap2.1软件，设置为基于产出导向的BCC模型对2016—2020年全国科技金融效率进行分析，结果如表2所示，效率的取值范围为［0，1］，得到的综合效率基于CCR模型计算得到的综合技术效率，不是纯粹的技术效率，而是在纯技术效率的基础上考虑了规模效益。所以，如果一个决策单位的综合效率为1，则其技术效率和规模效益必然为1。在这一阶段，我们认为，这一决策单元的投入—产出效率都是很高的，可以使这一区域的科技金融资源得到最优化的分配。如果某个决策单位的技术效率为1以下，说明这个决策单位的效率并不是有效的，其技术效率和规模效益中至少有一个是小于1的。通过实证分析，将31省市的科技金融资源配置效率划分为三个档次，区域综合效率为1时，说明区域内的科技和金融资源分配是有效的；当区域综合效率为［0.8，1］时，说明区域内科技和金融资源的配置是相对比较有效的，需要调整投入或产出松弛变量就能实现有效水平；当地区的综合效率值在［0，0.8］时，表明该地区科技金融资源配置存在较大问题，需要对投入变量和产出变量进行较大调整。

由表2可以看出，2016-2020年，山西、内蒙古、江西、山东、新疆的科技金融综合技术效率都是1。这说明，在一定的产出条件下，科技金融投资的规模和综合技术效率都是最好的。江苏、甘肃、北京、天津、河北、上海、安徽、福建、陕西、青海、宁夏的科技金融投资与产出都是比较有效的，经过适当的调节，可以使其达到一个较好的水平。其余15个省份的综合技术效率均处于［0.3，0.8］，离有效水平还有很大差距，有待进一步调整。

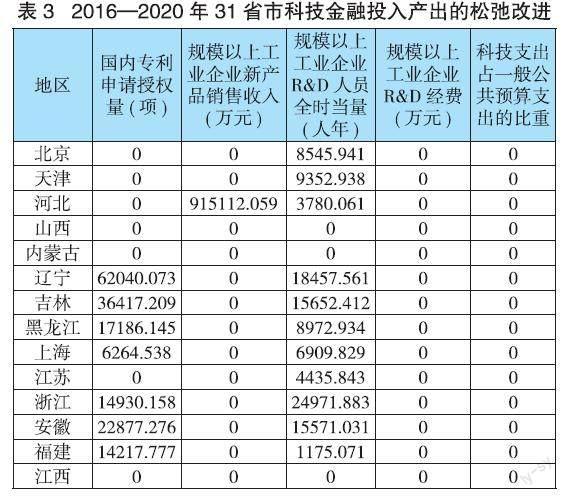
从表3可以看出，31个省市在2016—2020年间的科技金融投入和产出的松弛改进。若区域综合效率为1时，科技金融投入和科技金融产出的松弛改进值均不为0，该地区的科技金融资源配置效率仅仅是弱有效状态。可以通过增加科技金融投入或减少科技金融产出达到强有效状态；如果该地区综合技术效率值等于1，并且科技金融投入变量或科技金融产出变量的松弛改进值全都等于0，则认为该地区科技金融资源配置效率处于强有效状态。此时，该地区实现了科技金融资源配置效率的帕累托最优。

从表3可知，上海、浙江等12个省市需要减少专利申请授权量，河南需要减少新产品销售收入达到产出变量的最优状态；而北京、天津等18个省市企业研发人员较少，河南、广东、等5个省市研发经费较少，建议增加投入以实现投入变量的最优状态，最终实现帕累托最优。

五、结论与对策建议

研究结果表明，2016—2020年天津、山东等9个省市科技金融资源配置效率达到有效状态，其余22个省市未达到有效状态。其中北京、广东等9个省市的科技金融资源配置效率处于相对有效状态，只要稍加调整，即可达到有效水平。虽然随着科学技术水平的提高，我国科技金融发展迅速，但科技金融资源还存在浪费现象，资源配置效率还需要不断提升。为加快科技金融发展，推进创新型国家建设，实现经济高质量发展，本文提出以下建议：

一是推进金融产品更新升级，完善金融市场的参与机制，促进科技型企业和高新技术型企业的发展。创新融资方式，拓宽融资渠道，以商业银行等第三方金融机构为高科技企业提供信贷支持，针对科技企业轻资产的特点开展多种形式的融资贷款，如信用担保贷款、人才定价、知识产权和专利成果质押、公司股权质押等多种方式的贷款，创新金融服务产品，开发银保贷、投贷通等多种类型的金融产品。对符合上市条件的科技型企业加大培训工作力度。鼓励符合条件的科技型企业到科创板、创业板上市，完善多层次的资本市场。

二是充分发挥政府科技金融的供给引导作用和市场科技金融的需求追随作用。由于科技型企业高风险、高投资、周期长的特点，使得科技型企业在发展前期往往因为资金短缺、缺乏融资渠道面临创业失败的风险，需要政府科技金融发挥供给引导的作用，加大对科技型企业和高新技术型企业的扶持力度，运用财政和税收政策推动科技型企业的发展，引入风险投资机构和商业银行等第三方金融机构，扩大参与主体，形成投贷联动，充分发挥市场科技金融的需求追随作用。政府相关部门提高科技创新再贷款的额度，降低科技型企业和高新技术型企业贷款利率，引导市场资金流入科技创新领域，撬动社会资金促进科技创新。

三是充分发挥第三方科技金融服务机构的媒介作用，促进科技与金融加速融合。与商业银行等第三方金融机构合作，为科技型企业开展信用等级评价、投融资担保等专业服务，提供咨询业务解决科技企业的疑难问题，减少信息的不对称性，降低信息获取成本。對企业科技成果进行估价，对缺乏资金支持且拥有科技成果的企业，提供资金支持或科技成果转让。投融资机构以资金入股，提高股权的流动性，为企业解决融资问题和管理问题提供专业建议。

参考文献：

［1］张远为.湖北省科技金融资源配置效率研究——基于BCC模型和Malmquist指数法［J］.湖北社会科学，2021（09）.

［2］赵昌文，陈春发，等.科技金融［M］.北京：科学出版社，2009.

［3］Haslem John A，Scheraga Carl A，Bedingfield James P.DEA Efficiency Profiles of U.S.Banks Operating Internationally［J］.International Review of Economics and Finance，1999，（08）.

［4］Abdullah S，Shayem S.Financial Depth and Efficiency，and Economic Growth Nexus in Saudi Arabia and Oman［J］.Review of Economics and Business Studies， 2018，（11）.

［5］甘星，甘伟.环渤海、长三角、珠三角三大经济圈科技金融效率差异实证研究［J］.宏观经济研究，2017，（11）.

［6］陶立祥，沈俊，等.武汉市科技金融发展效率研究——基于BCC模型和Malmquist指数法［J］.科技管理研究，2020，（06）.

［7］杜金岷，梁岭，等.中国区域科技金融效率研究［J］.金融经济学研究，2016，（06）.

［8］贺宝成，李姗珊.我国省域科技金融效率时空演进分析［J］.合作经济与科技，2022（01）：54-56.

［9］李天籽，韩沅刚.武汉城市圈科技金融效率时空特征与趋同演化分析［J］.经济地理，2022，42（01）：61-69.

［10］张清叶，赵天宇.基于DEA-Malmquist的河南省科技创新效率研究［J］.科技创业月刊，2022，35（02）：36-42.

［11］成刚.数据包络分析方法与Max DEA软件[M].北京：知识产权出版社，2014.

［12］张鹏，李林欣，曾永泉.基于DEA-Malmquist指数的粤港澳大湾区科技创新效率评价研究［J］.工业技术经济，2021，40（02）：12-17.

基金项目： 2022年度济南市哲学社会科学规划研究项目（项目编号：JNSK22B17）。

作者单位：王永辉，齐鲁工业大学（山东省科学院）金融学院，研究生；邵林，齐鲁工业大学（山东省科学院）副教授，管理学博士。