基于不锈钢非线性应力- 应变模型的动车组专用污物箱静强度分析与应用

2022-05-30李宝国吕鹤婷

科学技术创新 2022年16期

李宝国姜军赵斌吕鹤婷

（中车山东机车车辆有限公司，山东济南 250022）

不锈钢材料具有将结构强度、耐久性及美学完美结合的独特优势，且具有防锈、防火、维护维修成本低等许多优点[1，2]，在近年来逐渐成为铁路客车污物箱制作的主体材料。大量的拉伸、压缩试验表明，单一的线性应力-应变曲线并不能真正很好的描述不锈钢材料的实际应力随应变的变化。为了得到更为吻合的不锈钢材料应力- 应变曲线，国内外专家做了大量的研究[3-7]。

针对目前国内污物箱分析时对不锈钢材料应力-应变曲线选用的不合理性，本文引入国际上较为通用的且在0～σ0.2范围内被广泛认可的经典R-O 模型作为不锈钢材料输入应力- 应变函数，利用其更加吻合实际应力随应变变化的特性进行污物箱静强度分析校核，得到了相较于线性应力- 应变曲线更为精确的分析结果。该非线性模型的引入可有效提高污物箱静强度分析的准确性，对于提高污物箱设计可靠性、减少材料设计浪费意义重大。

1 不锈钢材料力学特性分析

图1 为不锈钢与低碳钢材料的力学性能对比示意图，其中曲线A 代表低碳钢材料，曲线B 代表不锈钢材料，从图中可以明显看出，与低碳钢材料不同，不锈钢材料没有明显的屈服点，其屈服极限定义为产生0.2%的塑性应变所对应的应力，并称为名义屈服极限，用σ0.2表示；在名义屈服极限以下，只是在应力很低的范围，应力- 应变可近似认为成线性关系，在大部分范围内，应力-应变关系是明显非线性的。如果在污物箱强度分析计算时，将弹性模量作为一个常数输入，即将不锈钢材料的应力- 应变曲线看做固定斜率的线性函数变化，则会造成计算结果出现大幅偏差，从而影响设计准确性。

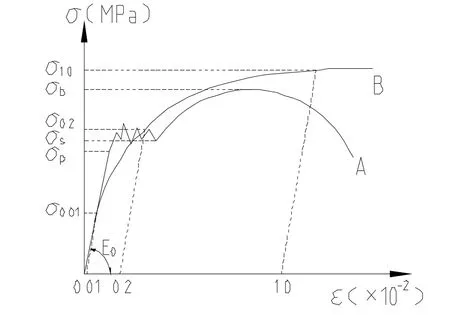
图1 不锈钢与低碳钢材料力学性能对比示意图[5]

本文引入的非线性材料的经典R-O 模型由Ramberg 和Osgood 提出，并由Hill 进行了修正[6]：

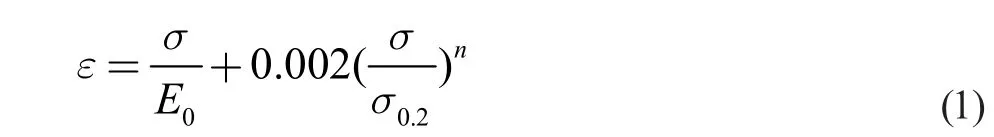
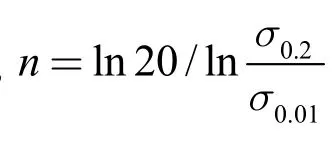
2 模型建立

污物箱的静强度计算一般是依据标准EN12663 的要求，使用有限元软件ANSYS Workbench 进行分析计算。

2.1 有限元模型

污物箱箱体采用316L 不锈钢材料，吊臂采用304 不锈钢材料；以污物箱箱体及吊臂作为计算模型，采用壳单元（Shell63）进行离散，吊臂与车体底架的连接采用三向弹簧单元（Combine14）进行模拟。整个装置共离散为64046 个单元，62855 个节点，离散模型见图2 所示。

图2 离散模型及约束与加载方式示意图

2.2 计算载荷及载荷工况

按照标准EN12663 的规定进行加载。在弹簧单元末端施加全约束，约束与加载方式如图3 所示。施加载荷的工况如表1 所示。

表1 载荷施加工况

2.3 材料力学性能

不锈钢材料304 和316L 基本力学性能如表2 所示。

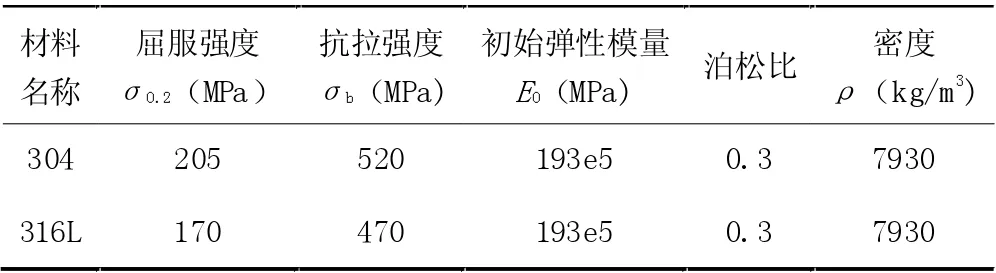
表2 不锈钢304 和316L 材料的基本力学性能

模型一：线性应力- 应变曲线模型

将不锈钢材料力学性能与普通低碳钢材料相类比，默认材料应力- 应变符合σ=E0ε，即应力与应变为线形关系，在计算过程中，将弹性模量作为一个常数（初始弹性模量E0）输入，这种计算方法即为静强度分析的线形计算方法。

模型二：非线性应力- 应变曲线模型

采用国际是常用的经典R-O 模型来对不锈钢材料应力不超过σ0.2的一段曲线进行拟合，将公式（1）引入到对污物箱静强度校核的有限元分析中，由n 引入的σ0.01，E0、σ0.2和σ0.01均由同一批次材料制作的试件的拉伸试验确定，n 通过计算获得。

2.4 静强度评估方法

在振动载荷及其组合工况作用下，污物箱及其联接结构上任意一点的应力均应小于相应材料的许用应力（316L 母材=170/1.0=170MPa，焊缝=170/1.1=154MPa（开坡口）；304 母材=206 /1.0=206MPa，焊缝=206/1.1=187MPa（开坡口））。

3 污物箱静强度分析

3.1 污物箱静强度应力对比分析

根据表1 的载荷施加，分别利用两种材料模型对污物箱静强度进行了校核计算，两种模型的计算应力值与参考许用应力和试验结果进行了对比（其中试验采用破坏性试验，无法得到具体每种工况的试验应力值，但是满足至少1.2 倍的安全系数，故，取参考许用应力与试验校核应力之比为1.2）如图3 所示。

从图3 中可以看出，模型1 的计算应力值明显偏大，远高于试验校核应力值，计算误差过大；而模型2 的计算应力值与试验校核应力值也有一定误差，但是误差值较小，在一定的可控范围内，说明模型二的计算精度更高，计算结果更可信。而且，模型1 的计算应力值已经大于参考许用应力值，这就可能造成实际设计时的人为加固、加厚等改进，从而增加了设计浪费和材料浪费。所以在进行污物箱静强度校核时，将不锈钢材料认定为应力- 应变非线性材料，并利用经典R-O 模型进行求解可以获得比利用线性材料模型求解更为精确的结果，从而可以有效的降低设计成本，节约材料，减少资源浪费。

当然，从图3 中可以看出，两种计算模型的结果都有一定误差，寻求一种更为合理的模型来真实拟合不锈钢材料的应力- 应变曲线，从而获得更为精确的计算结果，对于污物箱设计与优化意义重大。

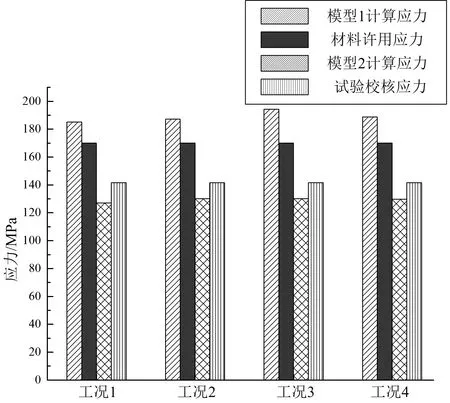
图3 模型计算应力与参考许用应力及试验结果比较

3.2 污物箱静强度应力云图分析与改进

基于3.1 部分的分析，采用经典R-O 模型可以获得更为精确的有限元分析结果，提取表1 四种工况下的应力云图，如图4 所示，分析其最大应力发生部位，应力分布状况，从而对污物箱优化设计提出可靠建议。

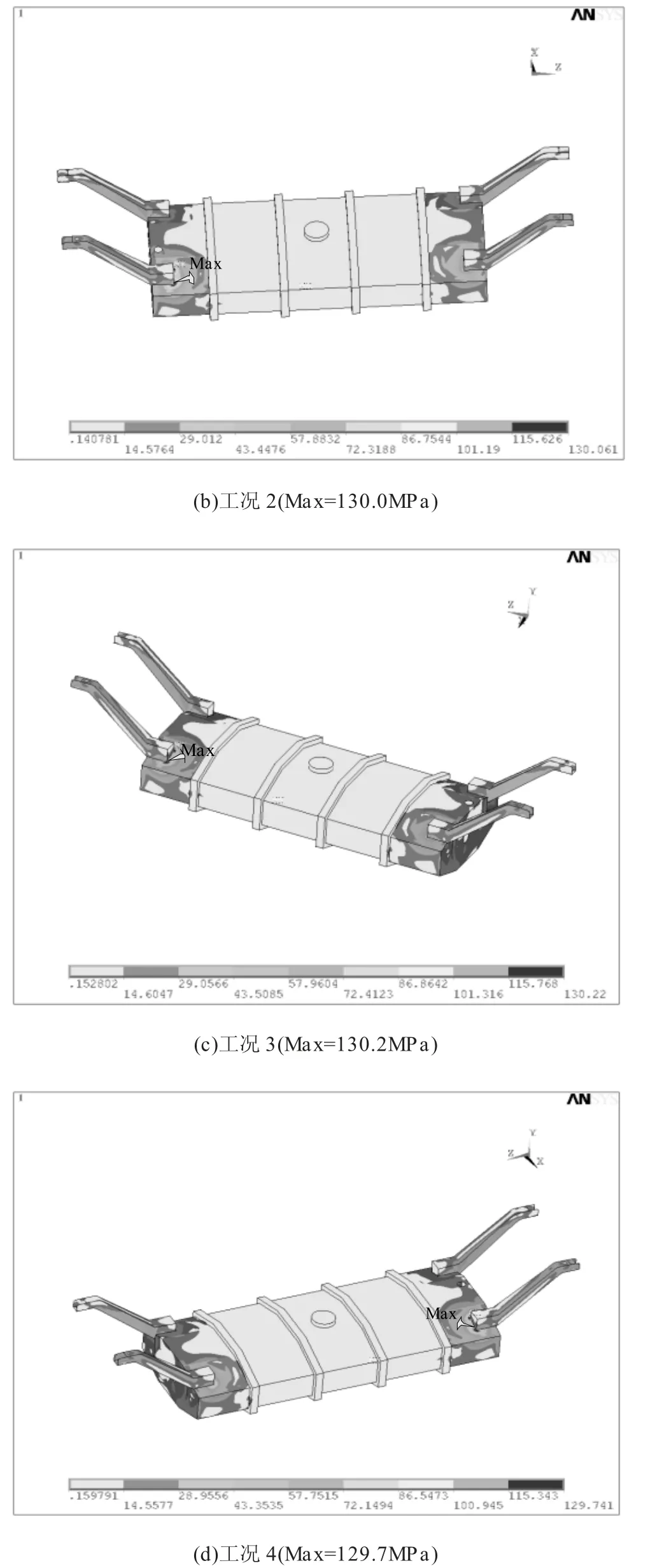
图4 不同工况条件下污物箱应力云图

从图4 可以发现，四种工况应力最大处都反生于吊臂与箱体连接焊缝处，而且应力分布也是从吊臂与箱体连接处逐渐向外扩散，并逐渐减小，且在沿吊臂方向应力集中较为明显。相对于普通材料与焊缝材料，焊缝处的应力普遍低于材料的许用应力。所以，针对污物箱应力集中的分析结果，在污物箱设计时需要对吊臂与箱体连接处的焊缝进行专门的加强，并保证焊接质量，以确保该焊缝处的稳定可靠。同时对吊臂及箱体与吊臂连接处周围的箱体部分也应进行专门校核及加强，可以适当增加此处加强筋的数量，保证承载强度。