基于多智能体深度强化学习的空间众包任务分配
2022-05-30赵鹏程于洪梅
赵鹏程, 高 尚, 于洪梅
(吉林大学 计算机科学与技术学院, 长春 130012)
众包(crowdsourcing)是一种利用人群智慧完成任务的计算范式. 随着移动互联网的快速发展和移动设备的普及, 空间众包(space crowdsourcing, SC)[1]成为一种新兴的众包类别. 在SC系统中, 首先请求者将时空任务提交到平台; 然后在差旅预算、 任务期限和技能要求等约束条件下进行任务分配或选择; 最后工人在截止日期前赶往指定地点完成任务并获得报酬. 目前, 任务分配作为空间众包中最基本的挑战, 得到广泛关注. 现有的工作存在以下不足: 1) 大多数只考虑工人或请求者单方面的利益, 若只考虑工人利益, 则会导致偏远地区的任务难以完成; 若只考虑请求者利益, 则任务分配可能会对某些工人不公平; 2) 通常只考虑强制工人合作或禁止工人合作的单一场景, 前者忽略了工人的情感和偏好, 而后者不利于工人和请求者利益的最大化; 3) 精确算法由于复杂度过高而难以在实际中应用, 而贪婪算法仅注重眼前利益, 只能得到次优解.
研究表明, 多智能体系统(multi-agent system, MAS)与众包系统的关键要素和过程联系紧密[2], 多主体技术可用来提高众包系统的自适应性和自组织性, 并解决任务分配、 任务分解、 激励机制设计等众包中的典型挑战. 此外, 深度强化学习(deep reinforcement learning, DRL)以Markov决策过程为理论框架, 考虑了动态环境下的即时回报和未来回报, 根据与复杂环境交互的经验, 直接拟合参数化模型学习最优策略, 在许多复杂的实际问题中都取得了成功. 近年来, 研究者们开始将注意力机制[3-5]引入DRL模型中, 通过有针对性地利用输入信息, 提升了模型的性能[6-7].
基于上述研究, 本文通过定义允许但非强制合作的空间众包(allow but not force cooperation spatial crowdsourcing, ABNFC-SC)场景, 利用基于A2C(advantage actor-critic)方法的多智能体深度强化学习(multi-agent deep reinforcement learning, MADRL)模型解决其中的任务分配问题. 优化目标是同时最大化任务完成率和工人收益率, 且本文设计了同时考虑请求者利益和工人利益的全局奖励函数. 为提升模型的性能, 引入注意力机制以指导智能体间的协作. 实验结果证明了本文方法的有效性、 鲁棒性和优越性.
1 预备知识
1.1 多智能体深度强化学习与A2C算法
多智能体强化学习是强化学习的思想和算法在多智能体系统中的应用[8-9], 其中各智能体在与环境互动和彼此交流中不断地学习和改进自身策略, 所有智能体协同工作以实现特定的目标[10]. 为解决更大规模和更高复杂度的问题, 研究者们将深度学习方法[11-12]与传统的多智能体强化学习算法相结合, 提出了多智能体深度强化学习.
演员-评论家(actor-critic, AC)算法是经典的强化学习方法, 该方法训练一个充当Actor角色的策略网络以产生最优化策略, 同时训练一个充当Critic的价值网络对Actor的动作进行打分, 并指导Actor的策略更新. 通过引入优势函数, 可得AC方法扩展为A2C方法[13], 实现了性能的进一步提升.
1.2 注意力机制
注意力机制的原理是通过训练参数化模型从输入信息中提取出与任务目标高度相关的信息, 排除干扰, 从而提高任务处理的效率和准确性. 本文采用经典Query-Key-Value模式的注意力机制[14], 其形式化描述为
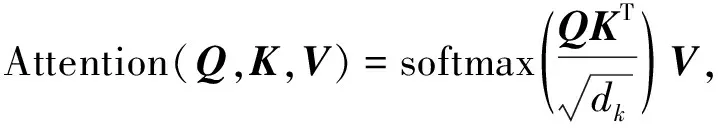
(1)
其中Q,K,V为特征向量,dk为Q(或K)的维度.
2 场景定义
本文所用的一些符号及其意义列于表1.

表1 符号及描述
2.1 任务和工人
在每个时间步, 任意任务tj(j∈[1,M])都可定义为一个七元组tj=〈l,a,d,b,r,f,Ψ〉, 其中:tj.l表示任务所在位置;tj.a表示任务被提交到平台的时刻;tj.d表示任务的截止时间;tj.b表示任务预算;tj.r表示任务半径, 即平台只为tj分配位于以tj.l为圆心、 以tj.r为半径范围内的工人;tj.f表示任务是否允许被多个工人合作完成,tj.f=1表示允许,tj.f=0表示禁止; 向量tj.Ψ=(ψ1,ψ2,…,ψNΨ)标记了任务的技能要求, 其中NΨ为所有任务要求技能的总数, 并且对∀k∈[1,NΨ],tj.Ψ.ψk=1表示tj要求对应技能,tj.Ψ.ψk=0表示tj不要求对应技能.
在每个时间步, 任意工人wi(i∈[1,N])都可以定义为一个六元组wi=〈l,v,ξ,f,μ,Ψ〉, 其中:wi.l表示工人的当前位置;wi.v表示工人的移动速度;wi.ξ表示工人在前往任务地点行程中单位距离的开销;wi.f表示工人是否愿意与他人合作,wi.f=1表示愿意,wi.f=0表示不愿意;wi.μ表示失败概率, 即wi有wi.μ的概率使任务失败(由于设备故障、 主观放弃等原因); 与任务中的对应定义类似, 向量wi.Ψ=(ψ1,ψ2,…,ψNΨ)标记了wi拥有的技能.
2.2 技能覆盖向量
为清楚表达工人wi对任务tj技能要求的满足程度, 同时为方便描述, 下面给出技能覆盖向量(skill cover vector)的概念, 其为一个NΨ维向量, 定义为

(2)
其中对∀k∈[1,NΨ], 有
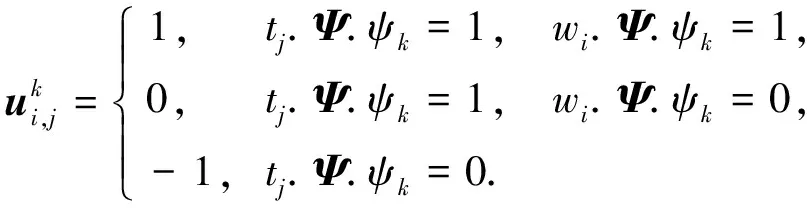
(3)
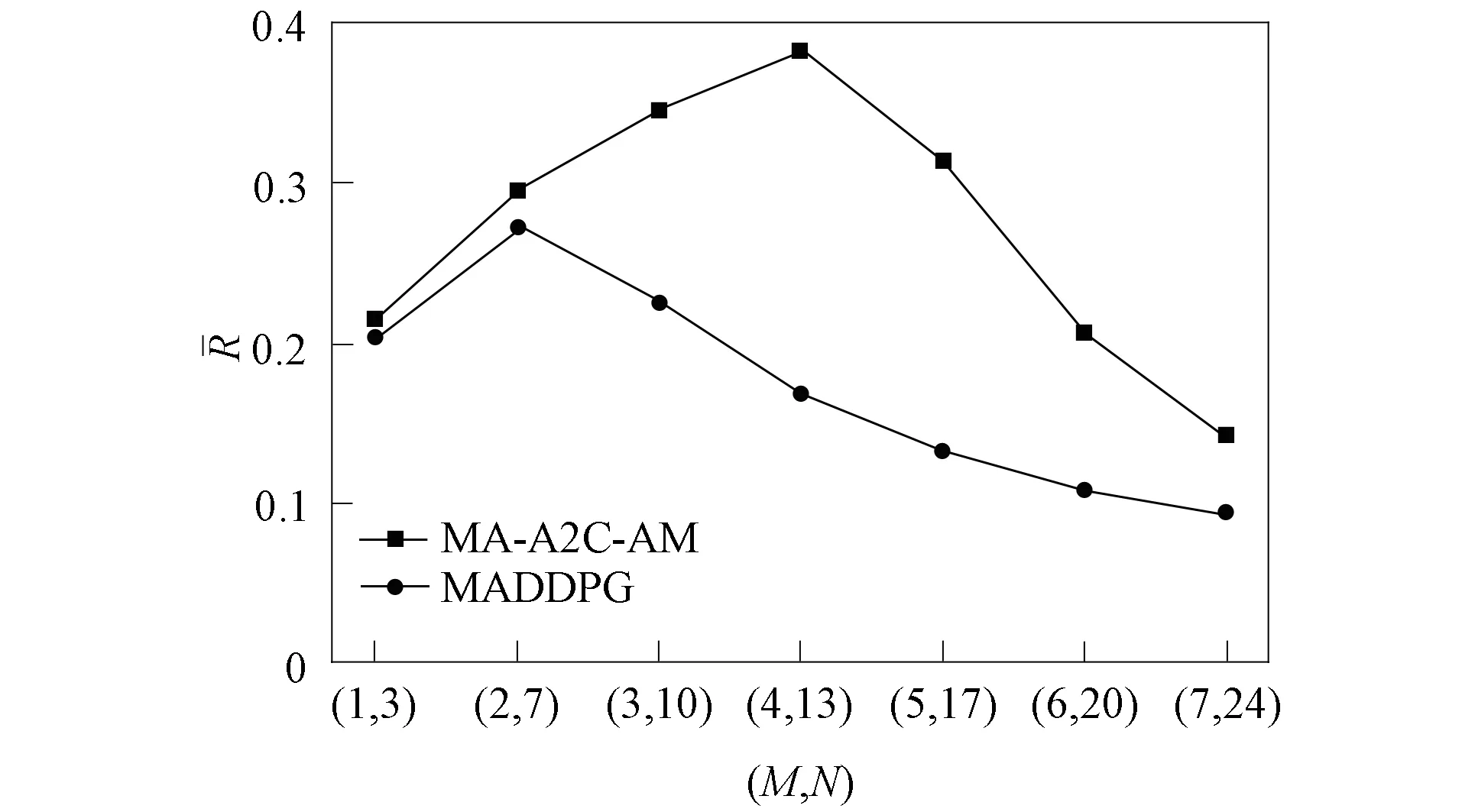
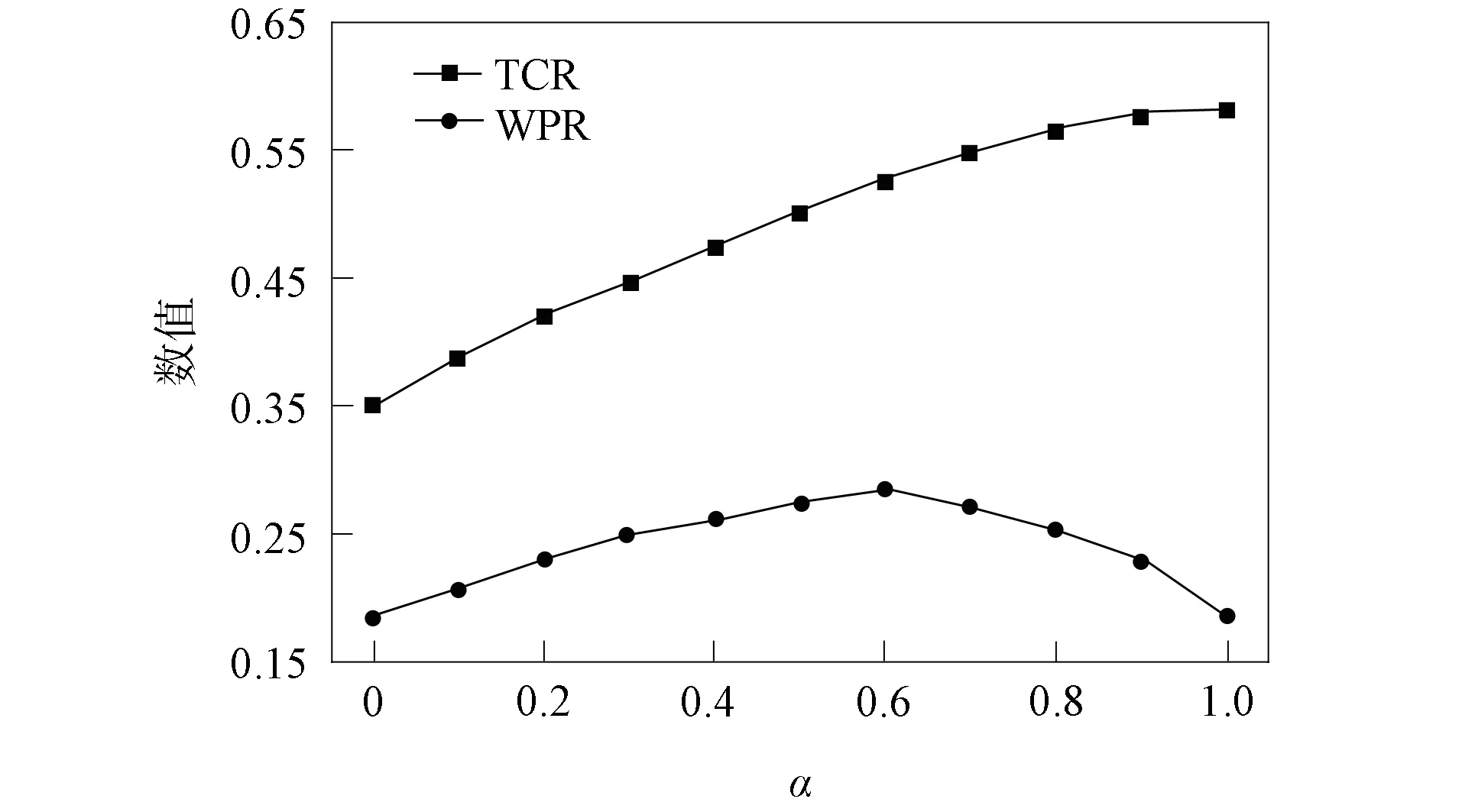
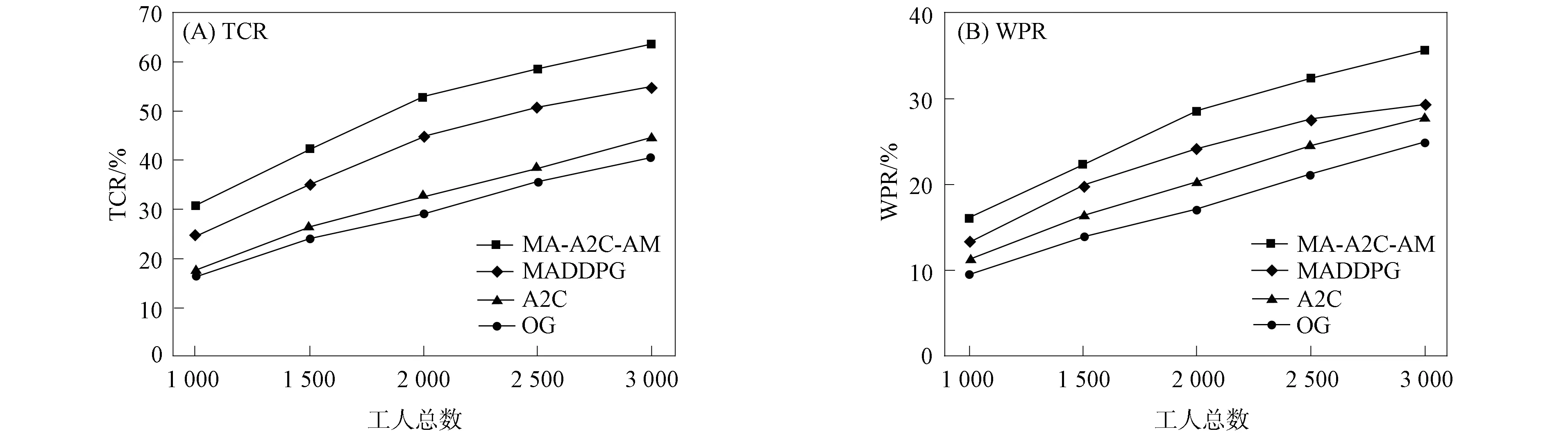
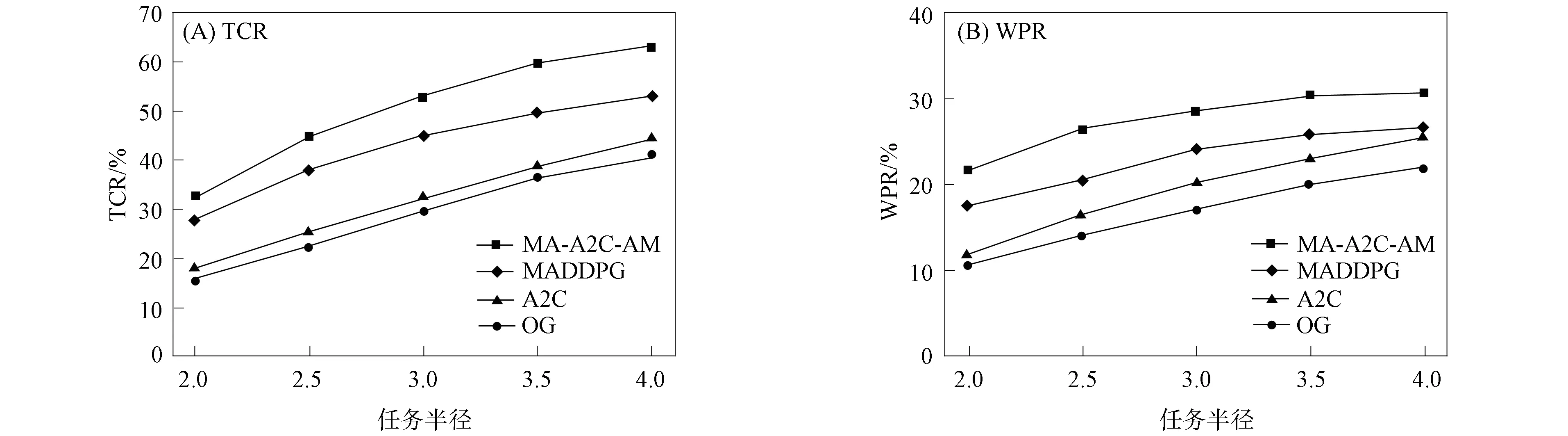
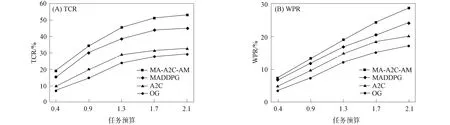
进一步, 为Up,j和Uq,j(0 (4) 下面给出wi成为tj的潜在工人的约束条件.潜在工人的含义:wi是tj的潜在分配对象, 但平台最终不一定会将tj分配给wi.约束条件如下. 1) 空间约束:wi必须位于tj的选择半径内, 即 dist(wi.l,tj.l)≤tj.r, (5) 其中不等号左边表示wi和tj之间的直线距离. 2) 时间约束:wi必须在tj的截止时间前到达任务地点, 即 route(wi.l,tj.l)/wi.v≤(tj.d-tj.a), (6) 其中不等号左边表示从wi.l到tj.l的路线长度. 3) 预算约束:wi的行程代价不得超过任务预算, 即 Ci,j=wi.ξ·route(wi.l,tj.l)≤tj.b. (7) 4) 技能约束: 在tj有技能要求的前提下, 如果tj禁止合作或wi不愿合作, 则wi必须具备tj要求的全部技能; 否则,wi只需具备至少一项tj要求的技能即可, 即 (8) 其中ones表示求向量中1的个数的函数. 基于上述条件, 定义参数Fi,j, 规定若wi和tj满足上述条件, 则Fi,j=1, 表示wi是tj的潜在工人; 反之,Fi,j=0, 表示wi不是tj的潜在工人. 下面给出由潜在工人组成的工人小组G可获得tj的必要条件. 1) 整体预算约束: 小组成员的行程代价之和不得超过任务预算, 即 (9) 2) 整体技能须满足tj的技能要求, 即令 UG=U1,j⊕U2,j⊕…⊕U|G|,j, (10) 则 ones(UG)=ones(tj.Ψ). (11) 特别地, 当|G|=1时, 上述条件即为单个潜在工人可获得tj的必要条件. 本文将每个工人建模为一个智能体, 但MADRL模型中智能体的个数和网络结构都是固定的, 因此MADRL只支持在固定个数的工人和任务之间进行匹配(设任务和工人的个数分别为M,N), 而现实中M个任务不一定恰好对应N个潜在工人.本文采用如下方法解决该问题: 在每轮匹配中, 首先利用下列每轮匹配中任务和工人选择算法确定实际参与匹配的工人集合W和任务集合T; 其次, 若|W| 算法1每轮匹配中任务和工人选择算法. 输入:M,N, 任务队列Qt, 可用工人集合SW, 计数器k; 输出: 参与本轮匹配的任务集合T和工人集合W; 1) 初始化:T=Ø,W=Ø,k=0 2) while TRUE 3)t←Qt.top( ) 4)G←GetPotentialWorkers(t,SW)//由约束条件, 从SW中找出t的所有潜在工人, 构成集合G 5) ifk+1≤M, |W∪G|≤Nthen 6)k←k+1,W←W∪G,T←T∪{t},Qt.pop( ),SW←SW-G 7) else 8) break 9) end if 10) end while. 图1 ABNFC-SC工作流程Fig.1 Workflow of ABNFC-SC 本文解决方案的思路如图1所示, 首先在训练阶段的每个时间步, 根据算法1, 由训练数据生成M个任务和N个工人/智能体(其中可能包含虚拟的任务或工人), 并由每个智能体根据自身的策略选择要执行的任务. 工人选择好任务后, 进入任务反选工人过程, 即对每个任务, 根据约束条件, 通过穷举搜索, 在选择了该任务的工人中选出能以最小代价完成该任务的工人或工人小组(如果存在这样的工人或工人小组). 然后程序模拟工人执行任务的过程, 并根据执行结果计算各智能体的立即回报. 最后, 根据立即回报更新MADRL模型参数并开始下一轮匹配. 重复以上过程直到训练结束. 注意, 尽管穷举搜索的复杂度较高, 但在本文研究的问题中, 选择同一任务的工人一般不超过5个, 因此穷举搜索是完全可行的. 在实际应用阶段, 任务被提交到平台后先进入任务队列等待, 当平台上等待的任务数量和对应的潜在工人数量达到匹配条件(即算法1中循环的退出条件)时, 平台即进行一次任务分配. 首先, 由训练好的MADRL模型在后台模拟工人选择任务; 然后, 运用穷举搜索, 平台反选工人并形成最终的任务分配方案发布; 最后, 获得任务的工人前往任务地点执行任务并取得报酬. 图2 MA-A2C-AM架构Fig.2 Architecture of MA-A2C-AM 本文提出具有注意力机制的多智能体优势演员-评论家(multi-agent advantage actor critic with attention mechanism)模型, 简称MA-A2C-AM, 其架构如图2所示. 为解决可扩展性问题, 本文采用去中心化结构; 为解决环境非稳定问题, 本文利用注意力机制计算其他智能体对智能体i的影响ci, 并将ci和局部观测oi一起输入价值网络Vωi, 使得Critic能根据局部观测和来自其他智能体的有效信息更准确地评估当前状态. 进一步, 本文同时将ci引入策略网络πθi, 使智能体学会彼此合作, 根据其他智能体的状态自适应地调整自身策略, 最终实现整体利益的最大化.图2中, i表示除智能体i外其他智能体的集合. 首先定义智能体i的局部观测oi为 oi={wi.f,Ii,1,Ii,2,…,Ii,M}, (12) 其中对∀j∈[1,M], 向量Ii,j表示与tj相关的信息, 表示为 Ii,j=(tj.f,tj.b,Fi,j,Ci,j,Ui,j), (13) 式中Ci,j为从wi.l到tj.l的行程代价.对智能体i, 其策略网络和价值网络的输入均为其局部观测oi和其他智能体信息对它的影响, 即由注意力机制计算出的上下文向量ci. 策略网络的输出是一个概率分布, 输出节点有(M+1)个, 其中前M个节点的输出值依次表示选择任务t1到任务tM的概率, 第(M+1)个节点的输出表示不选择任何任务的概率.价值网络只有一个输出节点, 其输出是一个实数, 表示对智能体i当前状态的打分, 即对智能体i在当前状态下的折扣累计回报估计. 在ABNFC-SC中, 工人之间本质上是相互协作的关系, 需要相互协作以完成共同的目标----最大化任务的完成率和工人的整体收益. 因此, 本文将奖励函数设置为任务完成率和工人收益率的加权和, 且所有智能体共享此奖励, 即对任意∀i∈[1,N], 智能体i在时间步τ的即时奖励为 (14) 其中α∈[0,1]为权重参数,Tτ和Mτ分别为第τ个时间步发布和完成的实际任务总数,Vτ为第τ个时间步发布的实际任务总价值(即预算之和),Pτ为第τ个时间步工人的总收益(即工人完成的任务总价值减去工人总的行程代价).这些量都可以在训练过程中根据工人执行任务情况及任务和工人的属性计算. 在时间步τ, 对任意智能体i, 首先用全连接层FC1_i对局部观测oi进行embedding操作, 得到ei.其次, 利用注意力机制由ei和ek(k∈i)计算出上下文向量ci, 然后将ei和ci输入第二个全连接层FC2_i_A和FC2_i_C, 再分别经过softmax层和linear层得到最终的策略和对当前状态的打分.最后, 根据策略产生动作aτ,i, 以所有智能体的联合动作Aτ=aτ,1×aτ,2×…×aτ,N与环境互动, 从而得到即时奖励rτ,i和新的观测oτ,i+1, 并进入下一轮迭代.期间, 智能体会收集轨迹数据并适时更新网络参数. 本文将策略网络的损失函数定义为 (15) 其中:τb和τe分别表示minibatch中的第一个和最后一个时间步;Aτ,i为优势函数, (16) γ∈(0,1]为折扣因子.式(15)同时包含了策略梯度损失和策略熵损失.策略梯度损失的作用是根据优势函数的正负增大或减小在未来采取相应动作的概率, 而引入策略熵损失的目的是鼓励智能体在训练初期多探索不同动作, 避免模型短期内贪婪地收敛到局部最优.超参数β通常是一个很小的正数, 用于确定熵项的相对重要性. 为提高价值网络对当前状态下预期回报的评估准确性, 本文将折扣累计回报和价值网络输出之间的均方误差作为价值网络的损失函数, 即 (17) 算法2MA-A2C-AM训练过程. 输入: 每个智能体的价值网络和策略网络; 输出: 网络参数{θi}i∈[1,N],{ωi}i∈[1,N]; 超参数:α,β,γ,|B|,T,ηθ,ηω//T表示训练的总步数; 2) repeat 3) 对∀i∈[1,N]: 智能体i根据πθi(·|oτ,i,oτ,i)执行动作aτ,i 4) 用联合动作Aτ=aτ,1×aτ,2×…×aτ,N与环境互动, 模拟工人执行任务 5) 对∀i∈[1,N]: 智能体i得到奖励rτ,i和新的局部观测oτ+1,i 6) 对∀i∈[1,N]:Bi←Bi∪{(τ,oτ,i,aτ,i,rτ,i,oτ+1,i,oτ+1,i)} 7)h←h+1,τ←τ+1,k←k+1 8) ifk=|B| or训练数据耗尽 9) 对∀i∈[1,N]: 对∀τ∈Bi, 计算Rτ,i;θi←θi-ηθθiL(θi);ωi←ωi-ηωωiL(ωi);Bi←Ø 10)k←0 11) end if 12) if 训练数据耗尽 13)τ←0,k←0, {Bi←Ø,o0,i}i∈[1,N] 14) end if 15) untilh≥T. 算法2给出了模型的训练过程. 在时间步τ, 首先对∀i∈[1,N], 智能体i根据局部观测和策略网络选择动作ai.然后程序模拟联合动作与环境的交互并计算即时奖励rτ,i, 同时每个智能体收集自身训练轨迹.当样本的数量达到minibatch规模或训练数据耗尽时, 每个智能体根据样本和价值网络计算折扣累计回报Rτ,i, 并通过小批量梯度更新策略网络和价值网络的参数. 如果训练数据耗尽但未达到总训练步数, 则使用原训练数据开始新一轮训练. 迭代以上训练过程, 直到达到总训练步数. 本文将MA-A2C-AM与MADDPG[15],A2C[13],OG[16](online greedy)等3种方法进行性能比较. 其中: MADDPG是经典的多智能体深度强化学习方法, 采用集中训练分散执行架构, Actor仅依据局部观测做出决策, 而集中式Critic根据所有智能体的观测为Actor打分, 在本文实验中, MADDPG的工作方式与MA-A2C-AM完全相同, 区别仅在于两者采用不同的强化学习模型产生策略; A2C是经典的单智能体强化学习方法, 同样采用Actor-Critic架构, 并利用优势函数降低估计的方差, 本文中A2C采用在线分配方法, 为每个新到达的任务选择合适的工人; A2C无法支持工人合作, 因为在合作场景下单智能体强化学习的动作空间随潜在工人数量呈指数增长; OG是一种在线贪婪算法, 其迭代地尝试将能以较低的成本覆盖更多技能的工人分配给当前任务, 直到完成任务. 所有基于强化学习的方法均使用式(14)作为回报函数. 本文使用任务完成率(task completion rate, TCR)和工人收益率(worker profitability rate, WPR)两项指标评价各算法的性能, 分别表示为 (18) (19) 表2 实验场景设置 本文将2013-01-01—2018-12-31的数据, 共1 778 108条, 用于训练, 剩余700 466条数据用于测试. Actor和Critic被同时训练, 以形成最佳任务分配策略, 但在测试时只需使用Actor产生动作, Critic被弃用. MA-A2C-AM,MADDPG和A2C均采用Leaky ReLU为激活函数, Adam为梯度优化器, 神经网络的权重和偏置均由机器学习库PyTorch默认初始化. 超参数β和γ统一设置为β=0.01,γ=0.98, 所有模型均训练100万时间步. 对MA-A2C-AM, FC1_i及注意力模块中的全连接层节点个数为24, FC2_i_A和FC2_i_C节点个数为64. 对MADDPG, Actor隐藏层设置为{32,16}, Critic隐藏层设置为{128,64,32}. 为增加早期探索,ε-greedy被用作行为策略, 且在训练的前3/4段,ε从0.8指数衰减到0.01.对于A2C, 其价值网络和策略网络隐藏层均为{64,32}, 并且任务的潜在工人上限设为5, 即在每轮匹配中, 若当前任务的潜在工人不足5位, 则以虚拟工人补充; 若超过5位(实验中该情况极少发生), 则选最先找到的5位. 其余超参数及训练时长列于表3, 其中训练时长取多次相同实验的平均值. 表3中, lr_a和lr_c分别表示Actor和Critic的学习率. 实验的软硬件设置为: 系统采用Ubuntu 16.04 LTS, 编程语言采用Python 3.7.4+PyTorch 1.0.0, CPU为Intel Xeon E5-2620×1, GPU为Tesla P40×1. 表3 超参数和训练时长 本文采用控制变量法进行实验, 可变参数为工人总数、 任务半径、 任务预算, 其取值见表2. 其中U(2.1,25),3.0,2 000表示默认值. 在每组实验中, 只改变其中一个参数, 同时保持其他参数为默认值. 在进行对比实验前, 需确定不同实验条件下M,N,α的最佳取值. 4.3.1 确定最佳M,N值 由于训练强化学习模型会耗费大量时间, 所以通过枚举(M,N)并进行大量实验确定所有实验条件下的最佳(M,N)不切实际, 因此本文结合有限的实验推断不同条件下(M,N)的合理取值.步骤如下: 1) 在表2所列的默认实验条件下, 取α=0.5, 对某特定M, 依次取M个连续的任务并根据算法1计算对应的潜在工人数量, 记为NM, 可得一系列NM.对这些NM求平均值并对结果取整, 将最终的结果记为N, 即得到了一个(M,N)对, 改变M, 最终得到一系列的(M,N)对, 即{(1,3),(2,7),(3,10),(4,13),(5,17),(6,20),(7,24)}. 3) 对于其他实验设置, 首先按步骤1)中的方法找出对应的(M,N)对, 然后选出N值位于步骤2)中最优区间中的(M,N)对, 如果有多个(M,N)对符合条件, 则将N值最小的(M,N)对作为最终结果.表4列出了不同可变参数下最终选定的(M,N)对. 4.3.2 确定最佳α值 为找到最合适的比例系数α, 本文考察了MA-A2C-AM针对不同α的表现.令α在0~1间以0.1为步长变化, 其余参数采用默认值, 观察MA-A2C-AM在TCR和WPR两个指标上的变化, 结果如图4所示.由图4可见, 当α>0.6时, TCR的增加变得缓慢, 同时WPR开始下降, 所以实现整体最大化的α值在0.6附近.进一步的实验证明,α对不同条件不敏感且MA-A2C-AM上的结论同样适用于MADDPG.因此, 在后续实验中统一设置α=0.6. 表4 不同实验条件下的(M,N)对 图3 (M,N)对对实验结果的影响Fig.3 Effect of (M,N) pairs on experimental results 图4 α对实验结果的影响Fig.4 Effect of α on experimental results 4.3.3 结果对比 确定了最佳的(M,N)和α后, 下面将MA-A2C-AM与其他3种任务分配方法进行性能对比. 工人总数对实验结果的影响如图5所示. 图5 工人总数对实验结果的影响Fig.5 Effect of total number of workers on experimental results 由图5可见, 随着可用工人数量的增加, 所有方法都可以更好地实现分配. OG虽然允许工人合作, 但其只贪婪地优化当前任务的分配, 形成了局部最优解, 因而表现最差. 由于A2C无法支持工人间的合作, 因此难以实现较高的任务完成率, 在TCR上仅略优于OG. A2C在WPR上相对于OG有较明显的优势, 表明A2C学习到了有利于长期目标的策略. MADDPG和MA-A2C-AM优于另外两种方法, 表明合作机制加上合理的分配策略, 能提高任务分配的效果, 也显示出多智能体强化学习在解决空间众包任务分配问题上的优势. 去中心化的MA-A2C-AM比集中式训练的MADDPG有更好的可扩展性, 可以在较多的任务和工人间进行匹配, 并且MA-A2C-AM中的注意力机制促进了智能体间的协作. 因此, MA-A2C-AM实现了优于MADDPG的分配策略. 图6 任务半径对实验结果的影响Fig.6 Effect of task radius on experimental results 任务半径对实验结果的影响如图6所示. 由图6可见, 图6中各方法的排名相对于图5没有变化. 随着任务半径的增大, 可用工人逐渐增多, 原来无法得到工人的任务可以被较远地方的工人执行, 因此TCR和WPR随之提高. 但距离越远的工人行程代价越高, 其收益也越低, WPR的增速随任务半径的增大而逐渐放缓. 特别地, 对于MADDPG和MA-A2C-AM, 尽管两者凭借较好的策略使更多的任务被工人合作完成, 但由于合作小组总的行程代价与小组规模成正比, 因此, 当任务半径大于3.0 km时, 尽管两者的TCR还略有增加, 但WPR却几乎不再增加. 任务预算对实验结果的影响如图7所示. 为简单, 在图7中, 任务预算区间用区间的左侧表示. 由图7可见, 不同方法的排名仍然没有变化. 过低的预算通常不足以抵消工人的行程代价, 而当预算超过任务半径内最昂贵的工人行程代价时, 即使再增加预算, 可用工人也不会再增加. 由图7(A)可见, 当预算区间在[0.4,0.9]时, 所有方法均较差, 而当预算大于1.7时, 所有方法的TCR几乎都不再增加. 而预算的增加直接导致了工人收益的增加, 因此图7(B)中WPR能持续增长. 图7 任务预算对实验结果的影响Fig.7 Effect of task budget on experimental results 综上所述, 针对目前空间众包场景单一、 分配方法难以兼顾请求者和工人双方利益的问题, 本文提出了一种基于多智能体深度强化学习的空间众包任务分配算法. 首先形式化定义了允许但不强制工人合作的空间众包场景, 然后设计了基于多智能体深度强化学习模型的分配算法. 为指导智能体间的有效合作, 引入了注意力机制; 为平衡请求者和工人双方利益, 设计了同时考虑双方利益的奖励函数. 对比实验结果表明, 本文方法均实现了最优的任务完成率和工人收益率, 证明了本文方法的可扩展性、 有效性和鲁棒性.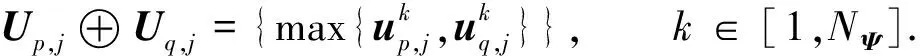
2.3 约束条件

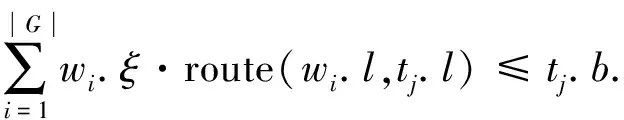
2.4 解决方案
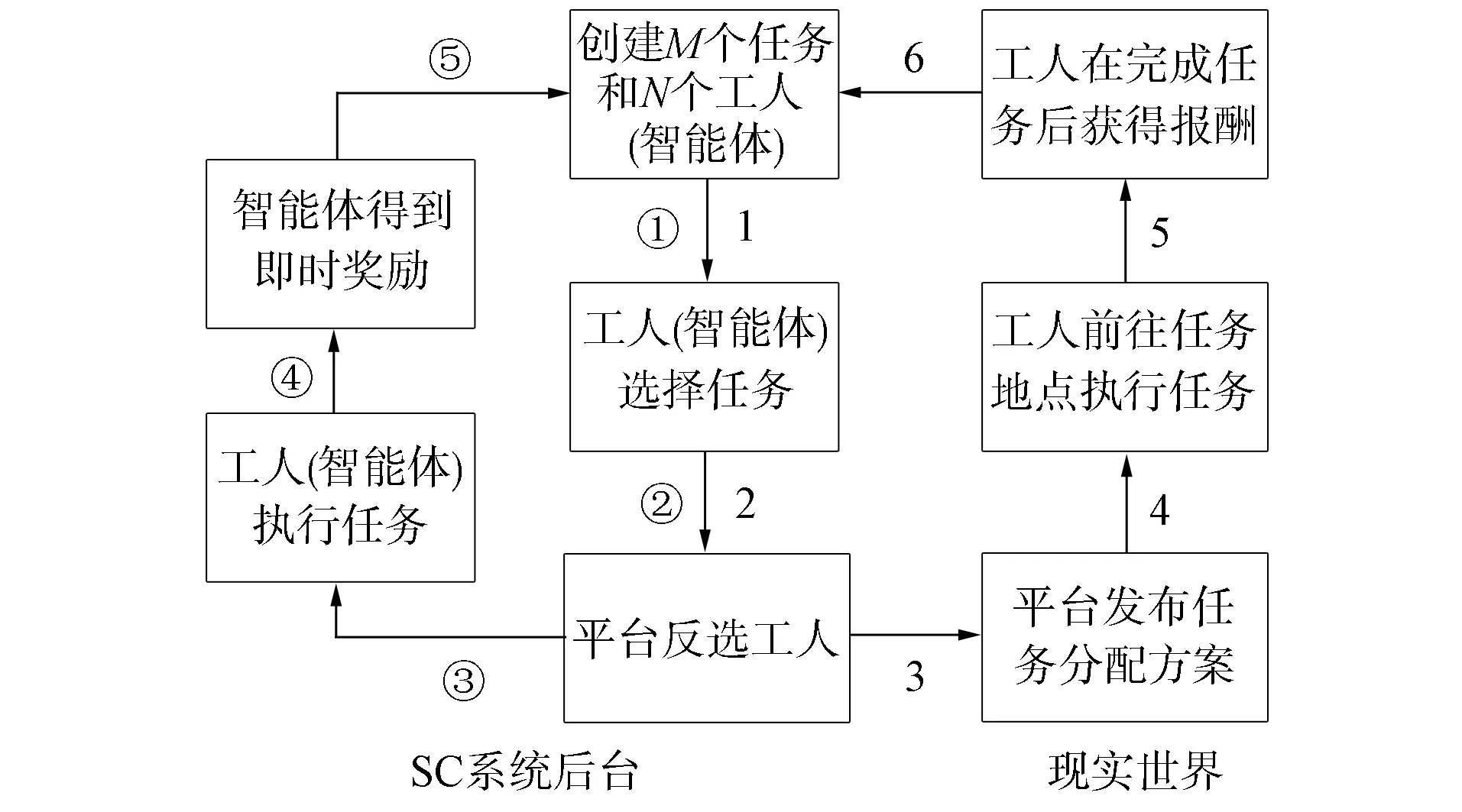
3 模型设计
3.1 模型概述
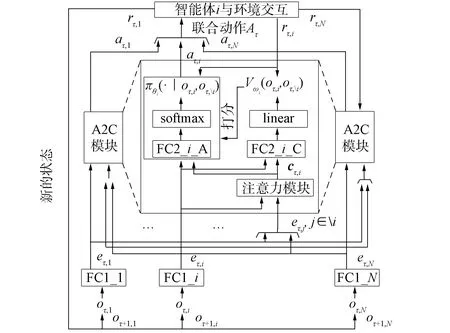
3.2 输入输出和奖励函数

3.3 工作流程
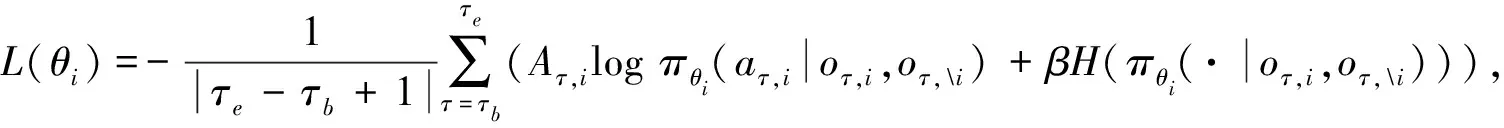
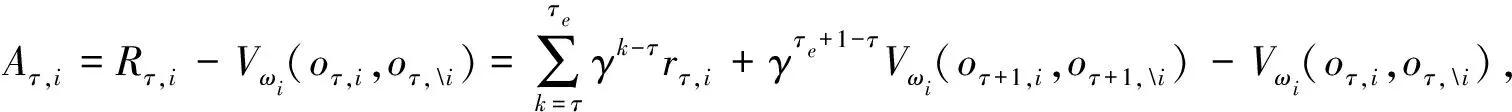
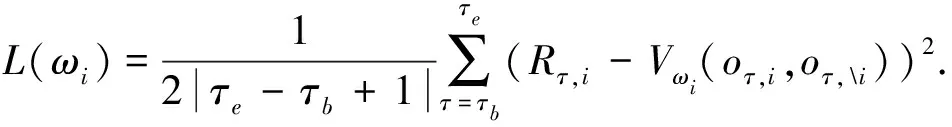
3.4 模型训练
4 实验分析
4.1 对比方法和评价指标


4.2 实验数据和基本设置


4.3 结果与分析

4.4 复杂度分析
