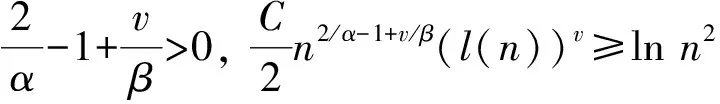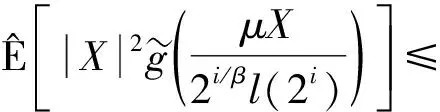次线性期望下WOD随机变量序列加权和的几乎处处收敛性

谭希丽, 张凯丽, 张 勇, 刘天泽

(1. 北华大学 数学与统计学院, 吉林 吉林 132013; 2. 吉林大学 数学研究所, 长春 130012)

1 引言与预备知识

定义1在次线性期望空间下, 如果存在某个有限的正实数序列{g(n),n≥1}, 使得下式成立：

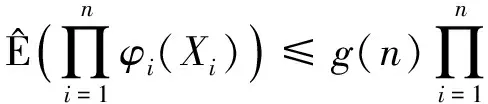
则称{Xn,n≥1}为上(下)WOD序列, 其中非负函数φi∈Cl,Lip()(i=1,2,…)是非降的(非增的).如果一个序列既是上WOD序列又是下WOD序列, 则称该序列为WOD序列.

显然, 如果{Xn,n≥1}是上WOD随机变量序列,f1(x),f2(x),…∈Cl,Lip()均为非降函数, 则{fn(Xn),n≥1}也是上WOD随机变量序列. 因为次线性期望下WOD序列包含NOD序列和END序列, 所以可将文献[12]中的定理2从概率空间NOD序列加权和的几乎处处收敛性推广到次线性期望下WOD序列加权和的几乎处处收敛性.

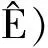
引理1[13]l(x)是缓变函数当且仅当

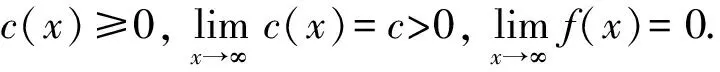
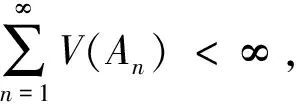
V(An, i.o.)=0,

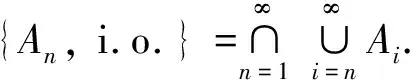
引理3[13]假设X∈H, 0<β<∞,φ(x)=x1/βl(x), 则对任意的C>0, 有

其中l(x)是缓变函数.

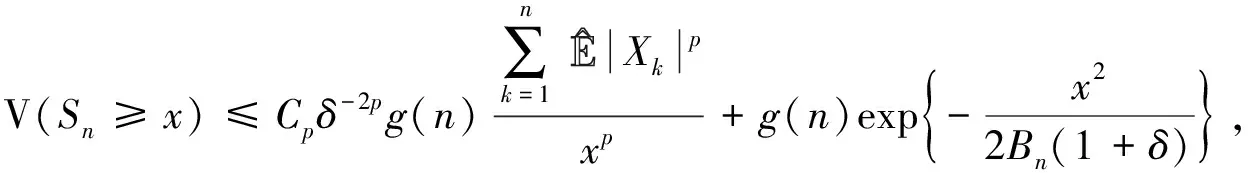
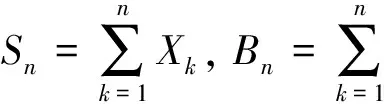
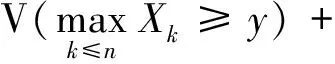
注意到

则有

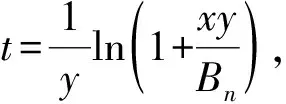
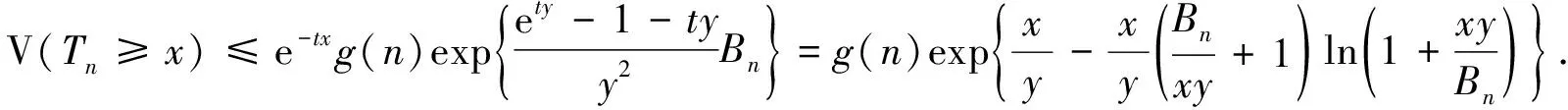
应用基本不等式

有

从而

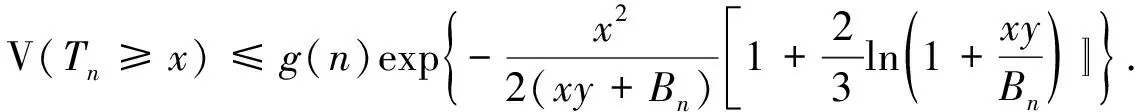
当xy≤δBn时, 有

当xy≥δBn时, 有

因此

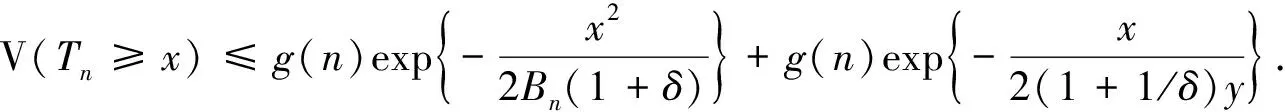
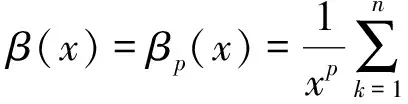
则有

易知

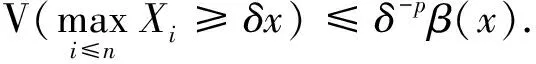
另一方面, 对任意的t>0, 有

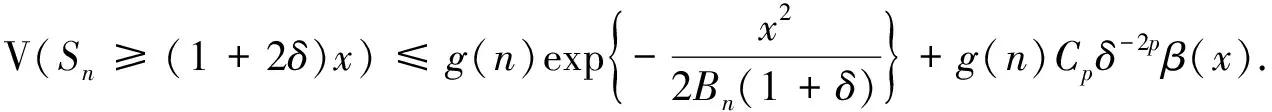
(2)

当β(x)≥1时, 不等式(2)显然成立.现设z=(1+2δ)x,δ′=(1+δ)(1+2δ)2-1, 则

同样是反对“厚葬”，墨子主张“节葬”，庄子似乎做得更彻底，更近于“露天葬”和“野葬”。从这个意义上讲，庄子是抗俗的先驱者，后世的抗俗者应该都从他那里得到过启发或受到过影响。

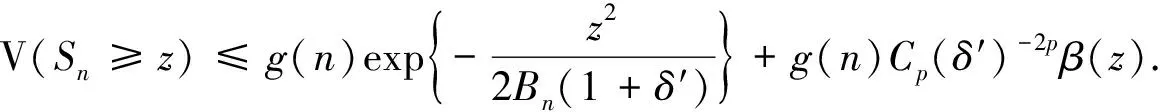
证毕.

2 主要结果

(3)

假设对任意的C>0,

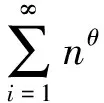
(4)

当1≤p<2时, 满足

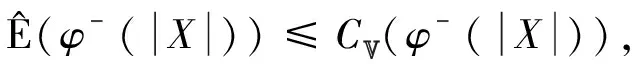
其中φ-是φ的反函数.则

(5)

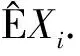
此外, 如果{Xn,n≥1}是下WOD随机变量序列, 则

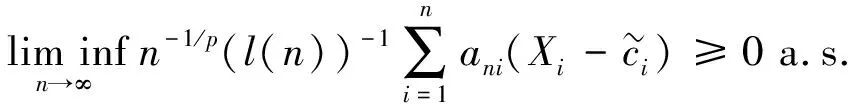
(6)

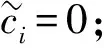
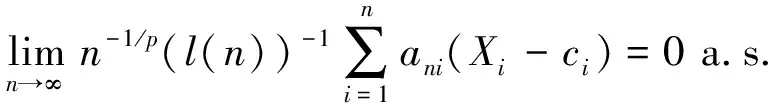
(7)

由于对数函数是最简单的缓变函数, 设l(n)=logn(n>1), 则可得如下推论.

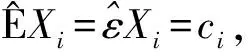
注1在次线性期望下, 本文将Ma等[13]的结果从END随机变量序列的几乎处处收敛性推广到了WOD随机变量序列的几乎处处收敛性.

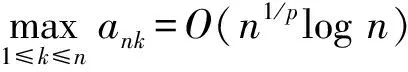
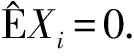
(8)

注意到

因此, 式(4)和式(9)表明

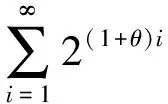
(10)

对于上WOD随机变量序列{Xn,n≥1}, 为确保截断后的随机变量也是上WOD随机变量序列, 需要截断函数属于Cl,Lip并且是非降的.在这种情形下, 对任意的1≤i≤n,n≥1, 定义

Xni=-n1/βl(n)I(Xi<-n1/βl(n))+XiI(|Xi|n1/βl(n)),

Yni=Xi-Xni=(Xi-n1/βl(n))I(Xi>n1/βl(n))+(Xi+n1/βl(n))I(Xi<-n1/βl(n)),

则{Xni, 1≤i≤n,n≥1}和{Yni, 1≤i≤n}都是上WOD随机变量序列.易得

因此要证明式(5), 只需说明

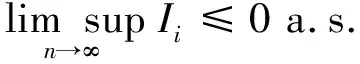
(11)

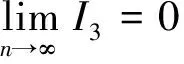
(12)

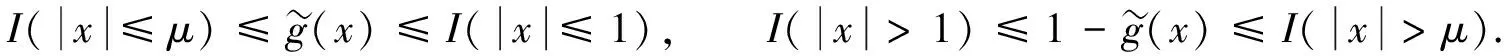
(13)

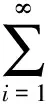
(14)

(15)

(16)

与文献[13]的证明类似, 可知式(12)成立.

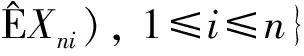
利用Cr不等式, Hölder不等式及式(8),(10),(13),(15),(16), 有

下面证明I22<∞.

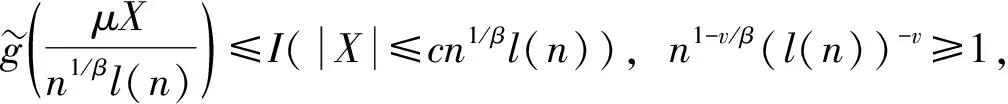
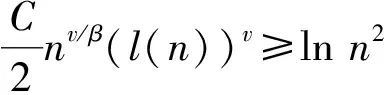
当α>2时, 取v∈(β(1-2/α),β).因为n1-v/β(l(n))-v≥1, 故有