带翼缘钢筋混凝土剪力墙塑性铰长度研究

王 斌，史庆轩，吴梦臻

带翼缘钢筋混凝土剪力墙塑性铰长度研究

王 斌1, 2，史庆轩1, 2，吴梦臻1

(1. 西安建筑科技大学土木工程学院，西安 710055；2. 西安建筑科技大学结构工程与抗震教育部重点实验室，西安 710055)

为了满足建筑功能的需求，正交方向布置的一字形墙通常被连接成一体，形成不同截面形式的带翼缘剪力墙．T形截面剪力墙作为其中最典型的墙肢组合形式，其截面的不对称性会导致不同受力方向下的变形性能和塑性铰长度存在明显差异．为了揭示T形截面钢筋混凝土(RC)剪力墙塑性铰的形成和发展机制，建立了T形墙精细化有限元分析模型．在验证模型有效性的基础上，通过分析T形墙沿高度方向的应变和曲率分布，定义了T形墙塑性铰长度的取值方法，进而分析了塑性铰长度在全过程受力中的变化规律，并结合T形墙的损伤机理和截面应变分布详细阐释了不同设计参数对塑性铰长度的影响．研究结果表明：T形墙在翼缘受拉方向的塑性铰长度主要由受压混凝土的压碎范围决定，且取值相对较小，在整个加载历程中呈现先快后慢再快的增长趋势；而翼缘受压方向的塑性铰长度完全由受拉钢筋的屈服范围决定，其增长速率呈现不断减小的趋势．基于参数分析结果，提出了一种考虑弯矩梯度、剪切效应和纵筋滑移贡献的T形墙塑性铰长度简化计算公式．通过与试验结果的比对，验证了简化公式的准确性．所提公式符合T形墙的变形特征，且可应用于L形墙．研究成果可为带翼缘面RC剪力墙基于变形的抗震设计和性能评估提供依据．

钢筋混凝土；T形墙；有限元分析；塑性铰长度；简化计算

强震作用下，钢筋混凝土(reinforced concrete，RC)剪力墙会率先在其底部发生损伤并产生不可恢复的塑性变形，形成“塑性铰”．随着荷载和变形的持续增大，钢筋沿墙肢高度方向逐步屈服，剪力墙的损伤也从其底部截面扩展至一定的范围，该塑性变形区域即为塑性铰长度．通过该区域内的塑性变形，剪力墙可吸收并耗散地震输入的能量，以减轻地震造成的破坏．因而塑性铰长度的大小一定意义上反映了剪力墙延性和耗能能力的强弱，也是衡量剪力墙抗震性能的重要指标．此外，在基于位移的抗震设计中，塑性铰长度的取值是计算边缘约束构件范围和箍筋配箍率的基础，也是基于塑性铰模型预测构件变形的关键，同时既有结构抗震加固时也需要依据塑性铰长度确定加固范围．因此，合理预测塑性铰长度对于指导工程设计具有重要意义．

目前，国内外对RC构件塑性铰长度的研究主要集中于梁柱构件[1-4]，对于剪力墙塑性铰长度的研究相对有限．已建立的RC剪力墙塑性铰长度计算模型主要采用以下3种方法：一种是由Paulay等[5]在研究地震作用下钢筋混凝土构件塑性铰的形成和发展机制时提出，将影响塑性铰扩展的3种因素(弯矩梯度、剪切变形和纵筋滑移)进行线性组合而得到的计算公式；另一种是采用试验研究或数值模拟的方法分析不同参数对剪力墙塑性铰长度的影响，通过参数拟合与回归分析建立塑性铰长度计算公式[6-10]；再有一种是假定极限状态下曲率沿墙高呈双线形分布，两段直线的交界点位于达到屈服弯矩的截面，认为屈服弯矩和极限弯矩间的区域为塑性铰长度，并根据屈服弯矩与极限弯矩间的比例关系建立计算公式[11]．以上提出的塑性铰长度计算公式所考虑的影响因素各不相同，各公式间计算结果的差异也较大，且仅适用于一字形墙．

结构平面布置时，一字形墙通常被组合成T形和L形等异形截面剪力墙，即带翼缘剪力墙．试验研究和数值分析[12-13]均表明带翼缘剪力墙在不同受力方向下的抗震性能存在显著差异，翼缘受拉方向具有更高的承载力和刚度，而翼缘受压方向具有更好的变形能力和耗能能力．此外，相比于普通一字形墙，带翼缘剪力墙具有更高的抗弯承载力，因而剪切变形所占比重更大，斜裂缝对塑性铰长度的影响也更显著．然而，目前针对带翼缘剪力墙塑性铰长度的研究相对匮乏，仅Bafti等[14]通过动力时程分析研究了工字形墙塑性铰长度随截面尺寸、轴压比和地震动参数的变化规律，提出了相应的经验计算公式；Hoult  等[15]分析了低烈度区U形墙在强轴和弱轴方向的等效塑性铰长度，并分别针对翼缘受拉和翼缘受压方向提出了等效塑性铰长度的简化计算公式．对于高层剪力墙结构中常见的T形和L形截面RC剪力墙，目前对其塑性铰长度的研究却鲜有报道，特别是对于此类异形截面剪力墙在不同受力方向下塑性铰长度的形成机制、影响因素和计算模型有待展开研究．

为此，本文通过对T形截面带翼缘RC剪力墙的精细化有限元分析，分别针对翼缘受拉和翼缘受压方向，研究带翼缘剪力墙塑性铰长度在全过程受力中的变化规律，分析不同设计参数对塑性铰长度的影响，结合数值计算结果，提出多参数综合影响下带翼缘剪力墙塑性铰长度的简化计算公式．

1 有限元模型

1.1 模型的建立

为了建立精确实用的剪力墙数值分析模型以便于进行塑性铰长度分析，本文选取文献[12]中的T形截面RC剪力墙试验试件TW-1和L形截面RC剪力墙试件LW-1，采用非线性有限元软件ABAQUS对其拟静力加载试验进行数值模拟，剪力墙高2200mm，其截面尺寸和配筋如图1所示．试验轴压比为0.1，混凝土轴心抗压强度为30.68 MPa，纵筋屈服强度为478 MPa．

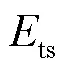
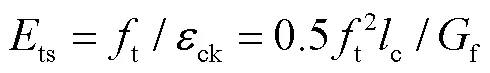
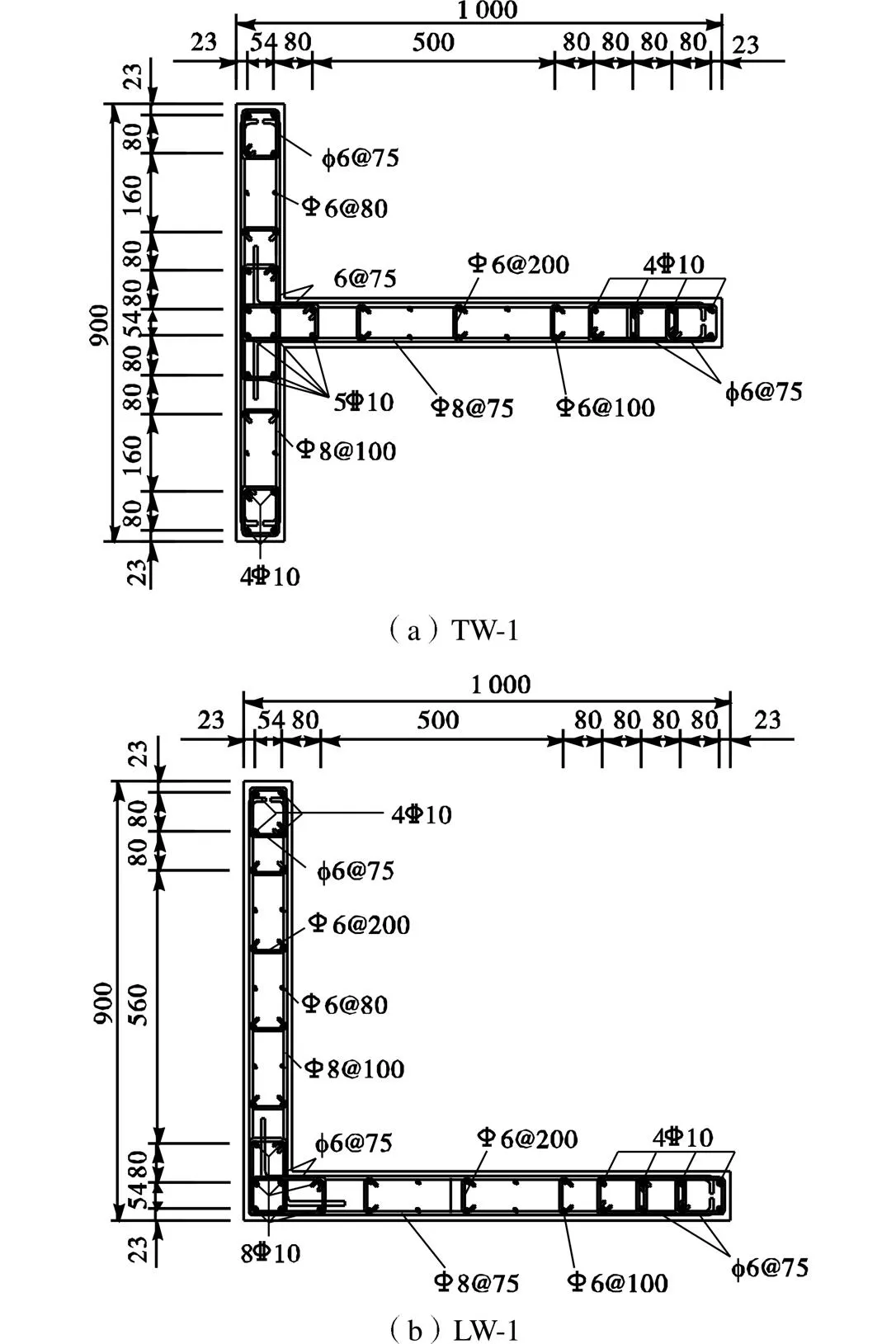
图1 截面尺寸和配筋

混凝土采用实体单元C3D8R，纵筋、分布钢筋以及箍筋均选用桁架单元T3D2，钢筋骨架通过Embedded形式嵌入到混凝土单元中，使两者变形协调．根据试件在试验时的实际工况，在剪力墙底部和顶部分别绑定(tie)两个端块，并为了提高计算效率将其设为刚性体(rigid body)．下部端块通过Encastre命令约束其底面6个自由度．在上部端块顶面首先施加轴向荷载，再按照试验加载制度采用位移控制模式施加水平荷载．

鉴于网格尺寸对于有限元模拟结果的准确性有一定影响[19]，因此在数值分析前需进行网格收敛性分析．选取T形墙试件TW-1进行推覆分析，网格尺寸依次取为100mm×100mm、75mm×75mm、50mm×50mm和25mm×25mm，不同网格尺寸下试件TW-1的推覆曲线如图2所示．结果显示：网格尺寸为100mm和75mm时，计算得到的推覆曲线存在一定的波动性，而网格尺寸减小到50mm后，曲线趋于收敛．为了提升计算效率，并考虑塑性铰长度研究对于应变沿墙高分布的精确性和连续性的要求，后续分析将剪力墙高度方向的网格尺寸取为25mm，长度和厚度方向的网格尺寸取为50mm，图2也验证了此种网格划分下计算结果的准确性．

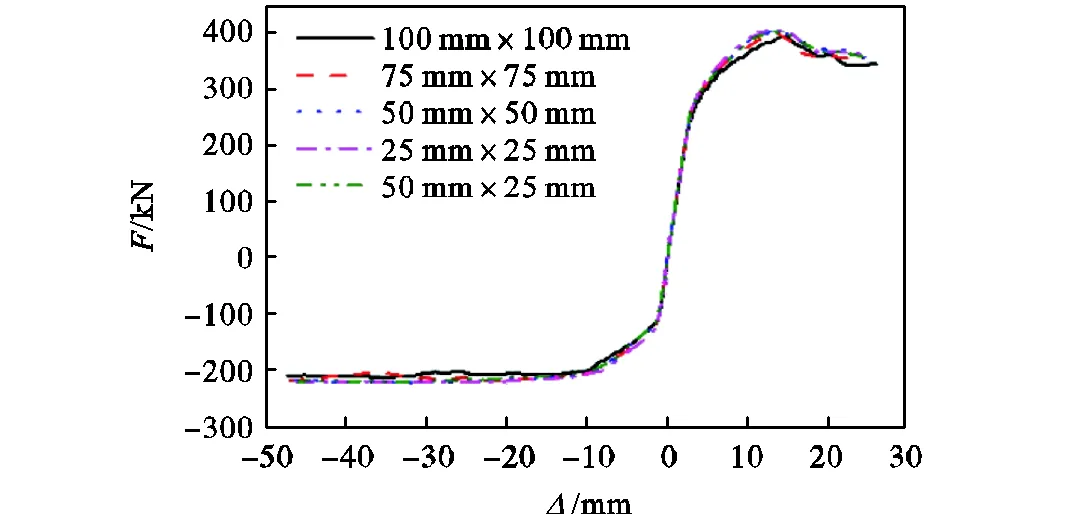
图2 网格收敛性测试

1.2 模型验证

图3为数值模拟与试验实测荷载-位移滞回曲线的对比，可以看出，模拟得出的承载力与试验值基本吻合，但模拟曲线的弹性段刚度大于试验实测刚度．这一方面是因为试验时剪力墙底部并不能做到如模拟一样完全固结，并且试验加载初期还受到装置间缝隙的影响，导致试验实测刚度偏小；另一方面是由于有限元计算方法是采用有限自由度近似模拟真实结构中无限个自由度，导致有限元计算刚度偏大．此外，模拟滞回曲线捏拢并不明显，这是因为有限元模型假定钢筋和混凝土之间变形协调，即不会发生黏结滑移，从而导致模拟结果与试验有一定的误差．但总体来看，本文所建立的有限元模型能较好地反映出带翼缘剪力墙的宏观受力性能．

图4对比了有限元模拟得到的损伤云图与试验试件TW-1的破坏形态，试验和模拟结果均表明，T形墙的损伤集中于无翼缘一侧的腹板端部，说明有限元模型能较好反映带翼缘剪力墙的局部受力特征．

考虑到后续研究涉及到应变层面的分析，有必要进一步对模拟得出的截面应变分布的准确性进行试验验证．试验在T形墙腹板一侧和翼缘外侧的每根纵筋和竖向分布钢筋上均布置了应变片，应变片位于距墙肢底部100mm高度处．提取试验实测的不同位移幅值下竖向钢筋(纵筋和竖向分布钢筋)的应变分布，并与有限元计算结果形进行对比．图5给出了翼缘受拉方向加载时应变的对比结果．可以看出模拟结果与试验数据相近，从应变层面验证了有限元模型的准确性．此外，腹板和翼缘的应变均呈曲线分布，且其非线性程度随位移的增大而增大，说明腹板和翼缘截面均存在剪力滞后效应．综上可见，本文建立的有限元模型可用作塑性铰长度研究．

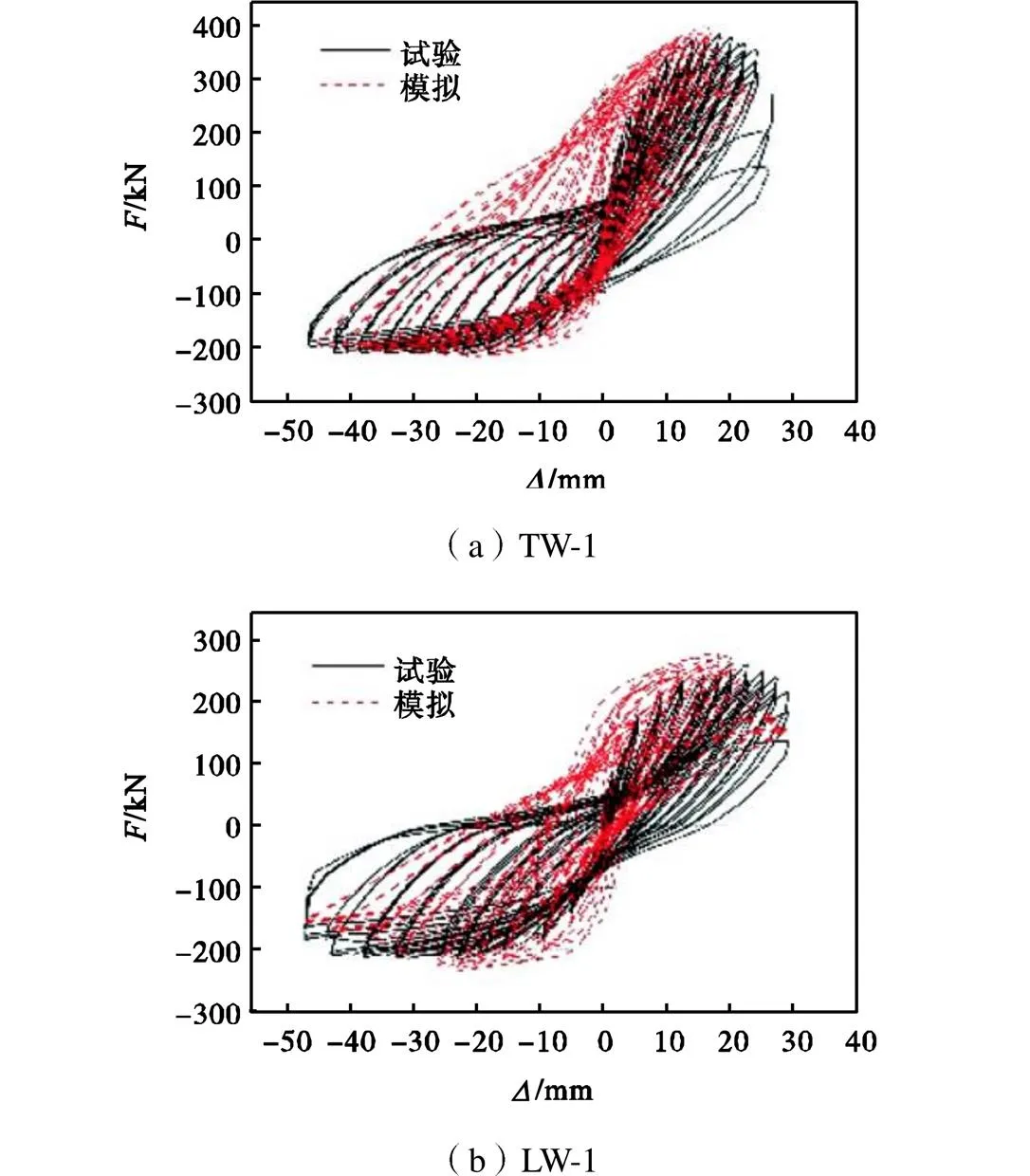
图3 模拟与试验滞回曲线对比

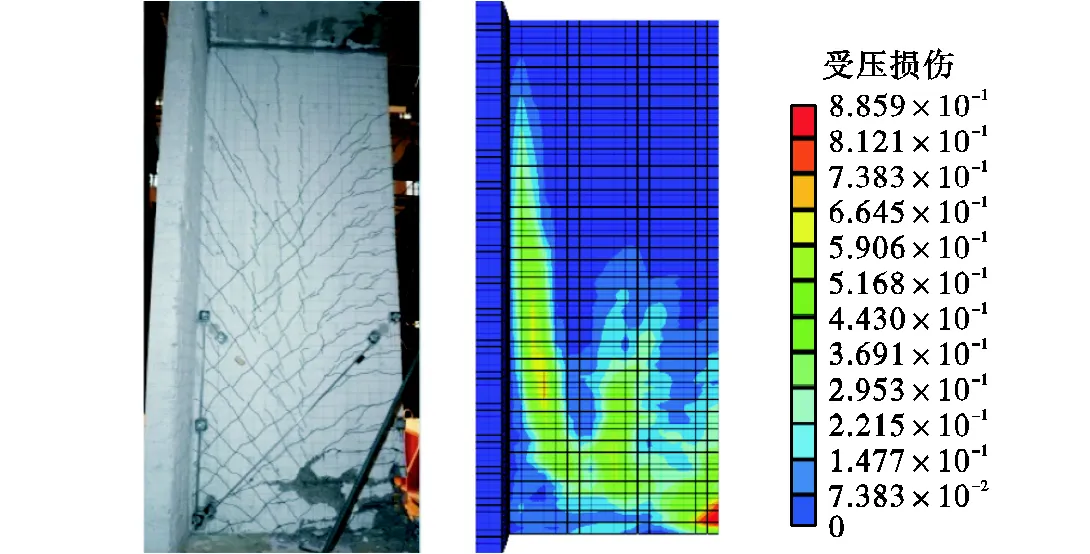
图4 模拟与试验破坏形态对比

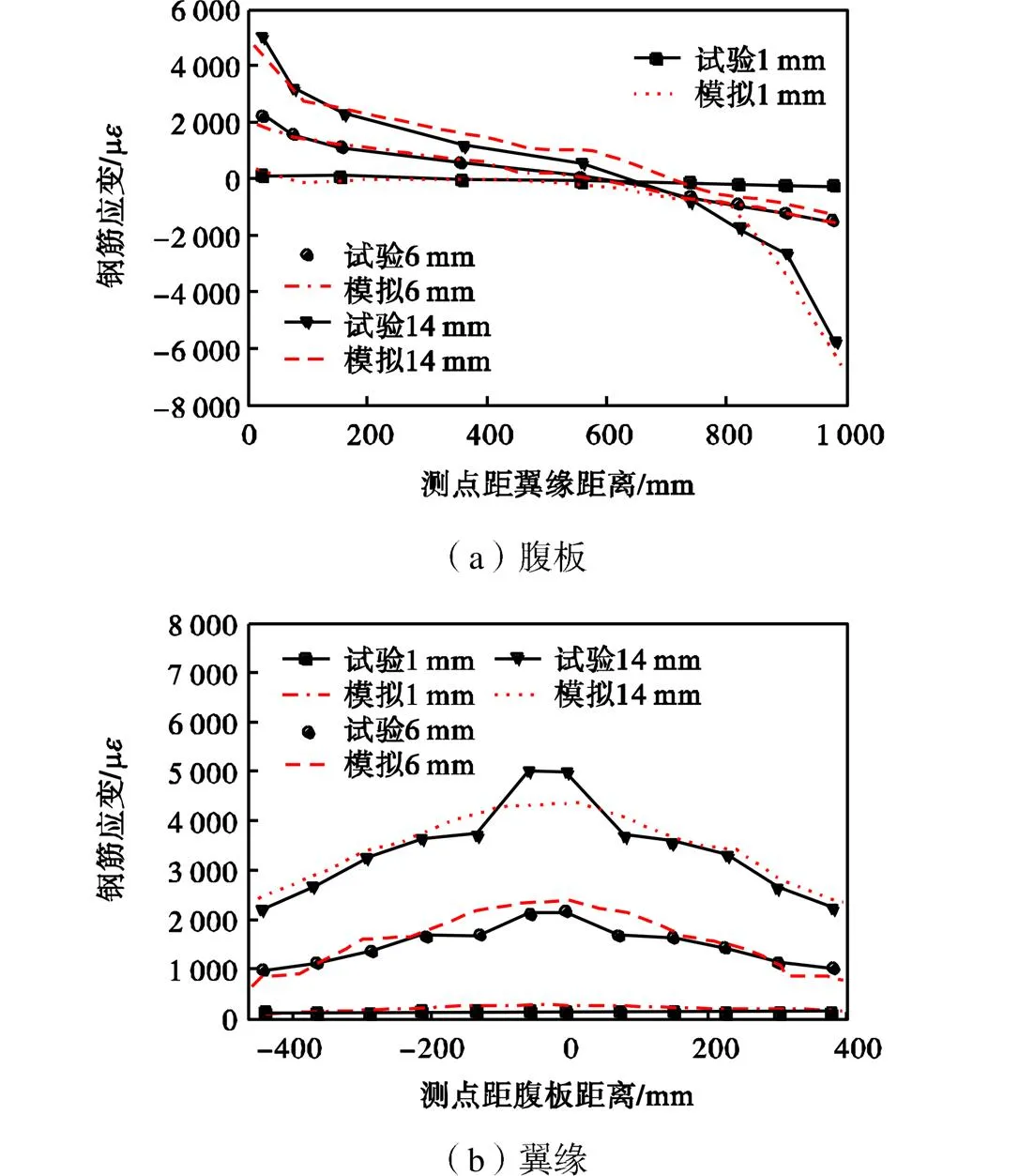
图5 模拟与试验竖向钢筋应变分布对比

2 塑性铰长度的确定

2.1 塑性铰长度取值方法的探讨

塑性铰长度作为一种抽象的性能指标，并不像应变和位移等可直接通过试验或数值模拟得到，而是需要借助构件的响应来间接确定．塑性铰长度通常有3种确定方法，分别是基于应变和基于截面曲率得到的实际塑性铰长度，以及基于位移计算出的等效塑性铰长度．以下分别就这3种方法展开讨论，并确定适用于带翼缘RC剪力墙塑性铰长度的取值方法．

2.1.1 方法1——基于应变的塑性铰长度确定方法

基于应变来确定塑性铰长度的方法是根据构件最外侧受拉钢筋的应变分布，将其达到屈服应变y的范围定义为塑性铰长度py．该种定义方法通常适用于受拉侧钢筋达到屈服应变先于受压侧混凝土达到峰值压应变的情况，即截面的屈服是由受拉侧钢筋控制的．这对于对称配筋的矩形截面构件以及T形截面带翼缘剪力墙翼缘受压方向是普遍成立的，如图6(a)所示．但对于翼缘受拉方向，由于其截面受压区高度较大，特别是在高轴压时受压区边缘混凝土可能率先达到峰值应变c0，并控制截面屈服，如图6(b)所示．因此，对于受压侧混凝土控制截面屈服的情况，更适于将受压侧边缘混凝土达到峰值应变的范围定义为塑性铰长度pc．

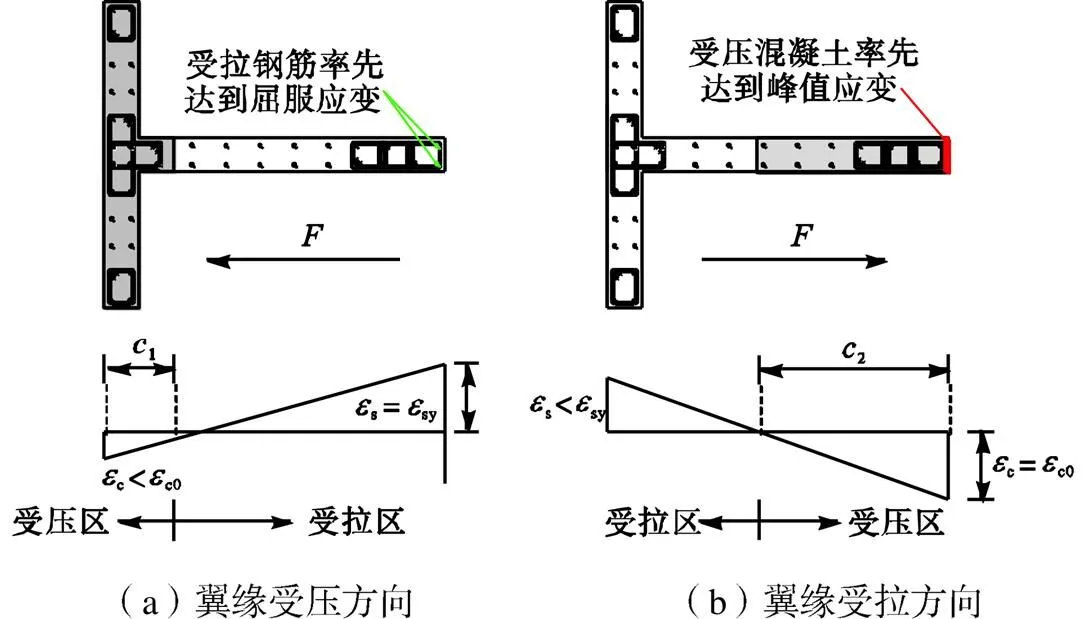
图6 不同受力方向下T形墙截面的屈服

2.1.2 方法2——基于曲率的塑性铰长度确定方法

基于曲率来确定塑性铰长度是上述基于应变方法的另一种表现形式，它首先通过截面拉压两侧的应变差值除以截面高度计算出某一截面的曲率，并依次得到曲率沿墙高的分布，将达到屈服曲率的区域取为塑性铰长度pf．此方法的优点在于可综合考虑拉压两侧塑性变形对塑性铰长度的影响，弊端在于确定塑性铰长度时需要计算出截面的屈服曲率．然而现有的屈服曲率计算式大都是经验表达式，计算结果的离散性较大，无疑增大了塑性铰长度取值的不确定性．远没有以屈服应变为量度的方法直观准确．

2.1.3 方法3——等效塑性铰长度

在进行RC构件变形能力分析时，由Paulay等[5]提出的塑性铰模型因其简便实用得到了广泛的推广．对于图7所示的顶部受一集中荷载的悬臂剪力墙，虽然其弯矩沿墙高呈线性分布，但其实际的曲率分布是非线性的，特别是在其底部塑性铰区内受裂缝和材料塑性变形的影响，曲率分布更为复杂．塑性铰模型是将剪力墙的实际曲率分布首先简化成分段线性分布，即沿墙高线性分布的屈服曲率y与塑性铰长度p范围内线性分布的塑性曲率p的叠加，极限曲率u＝y＋p．进而引入等效塑性铰长度的概念，并将塑性曲率分布等效为长度为pe范围内均匀分布的塑性曲率p．其中对屈服曲率y两次积分可得到墙顶屈服位移y，将塑性转角p乘以转动中心到墙顶的距离e即可得到墙顶塑性位移p，两者之和即为剪力墙顶点总位移，即有

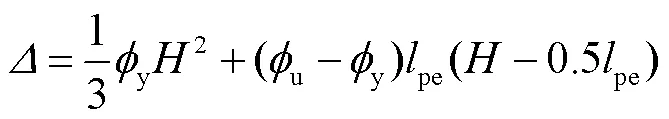
式(3)经过变换，可得到等效塑性铰长度计算式为

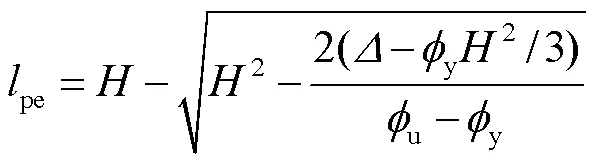
因此只要分析得到剪力墙的顶点位移，并通过公式计算屈服曲率y和极限曲率u，便可得到等效塑性铰长度pe．再根据等效前后塑性转角p相同的原则，即0.5(－y)p＝(－y)pe，即可得到塑性铰长度p，且p＝2pe．

依据塑性铰模型间接确定塑性铰长度的方法，可不再依赖于构件的细部响应(应变和曲率)，这有利于提高计算结果的准确性，因为依靠试验和模拟测得的应变值远没有其宏观响应(位移)准确可靠．然而，等效塑性铰长度的计算需建立在一定的假定基础上，其一是假定刚度沿墙高保持不变，即计算屈服位移时曲率呈线性分布．但是在墙肢中上部混凝土并未像底部一样开裂，所以该假设一定程度上高估了屈服位移，进而低估了塑性铰长度；其二是塑性铰模型未考虑剪切变形和纵筋滑移的影响，所以又高估了塑性铰长度．因此，基于塑性铰模型反算出的塑性铰长度不适于开展塑性铰长度的影响因素分析，但研究塑性铰长度的目的在于提出等效塑性铰长度计算公式，并应用于塑性铰模型进行变形能力计算．

综上所述，基于应变的塑性铰长度确定方法，因其数据采集简便、数值相对可靠、且无需计算假定，更适于进行塑性铰长度的研究．本文在进行带翼缘剪力墙塑性铰长度分析时，依次提取墙肢受拉侧最外层钢筋各单元的拉应变，得到钢筋沿墙高方向的应变分布，并将超过钢筋屈服应变(y＝0.00239)的区域取为钢筋屈服长度py；同时提取墙肢受压侧边缘混凝土各单元的压应变，得到混凝土沿墙高方向的应变分布，并将超过混凝土峰值压应变(c0＝0.002)的区域取为混凝土屈服长度pc，最后将py和pc的较大值取为塑性铰长度p．

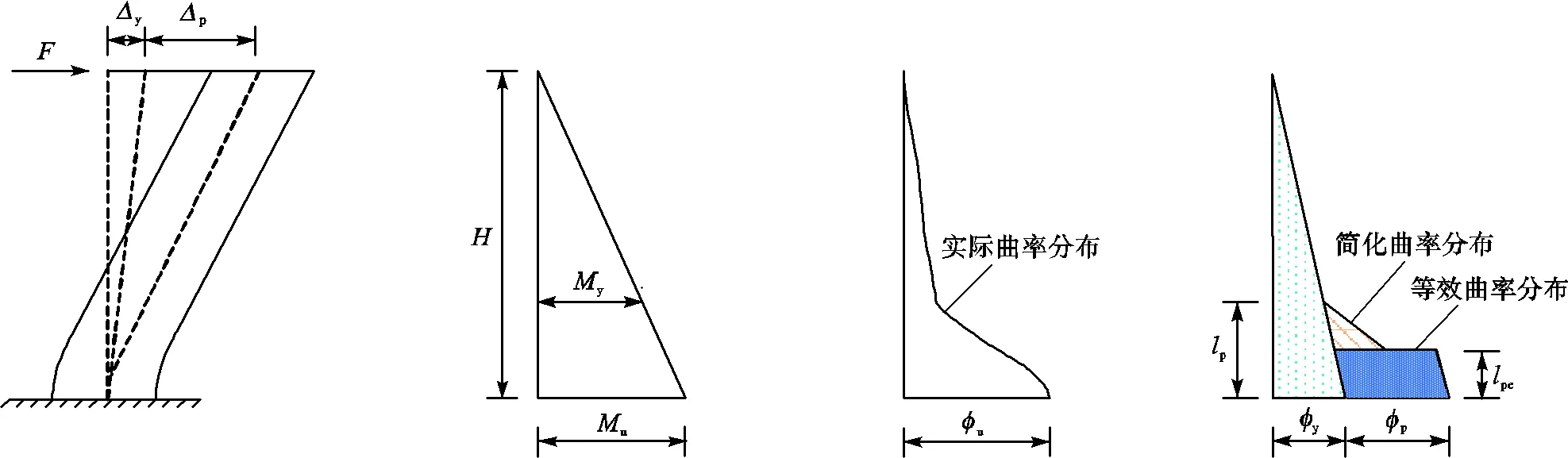
图7 塑性铰模型

2.2 不同取值方法下塑性铰长度对比分析

应用第1.1节建立的有限元模型对剪力墙试件TW-1进行有限元分析，分别得到极限状态下最外侧受拉钢筋应变、受压侧边缘混凝土应变以及截面曲率沿墙高的分布，如图8所示，并据此分别确定出基于方法1和方法2的塑性铰长度．同时将数值计算结果代入式(4)中，得到基于方法3的塑性铰长度．其中在运用方法2和方法3时，可依据文献[13]提出的公式计算T形墙的屈服曲率和极限曲率，分别得到翼缘受拉状态下的屈服曲率y＝0.00503和极限曲率u＝0.03483，以及翼缘受压状态下的屈服曲率y＝0.00427和极限曲率u＝0.0649．极限状态下3种取值方法确定出的塑性铰长度与试验试件的破坏区域的对比如图9所示．

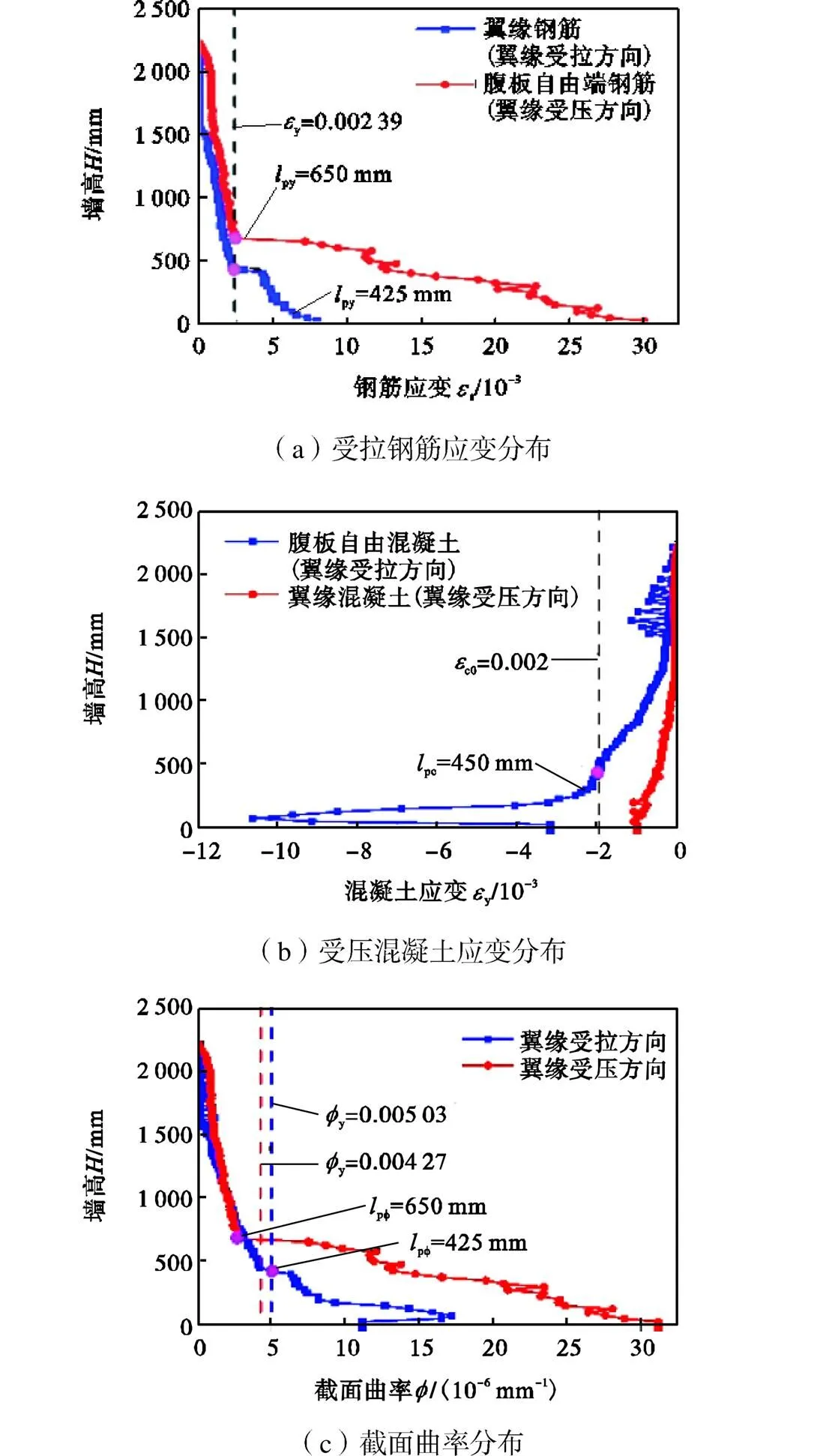
图8 极限状态下T形墙应变和曲率沿墙高的分布

由图8(a)可知，在极限状态下墙肢两侧最外层受拉钢筋均能达到屈服，且翼缘受压时腹板自由端钢筋的应变大于翼缘受拉时翼缘钢筋应变，同时翼缘受压时达到屈服应变的钢筋范围大于翼缘受拉时．由图8(b)可知，在极限状态下腹板自由端根部混凝土可达到峰值压应变，而翼缘内混凝土的应变值在整个墙高范围内均小于峰值压应变．综合来看，对于翼缘受拉状态，基于钢筋应变的塑性铰长度为425mm，而基于混凝土应变的塑性铰长度为450mm，因此翼缘受拉时塑性铰长度是由腹板自由端受压混凝土决定的，塑性铰长度取两者较大值450mm；对于翼缘受压状态，基于钢筋应变的塑性铰长度650mm，而基于混凝土应变的塑性铰长度为0，因此翼缘受压时塑性铰长度是由腹板自由端受拉钢筋决定的，塑性铰长度取两者较大值650mm．以上分析表明：对于T形截面带翼缘RC剪力墙，翼缘受拉状态和翼缘受压状态下塑性铰长度不仅取值大小不同，且取值的决定因素也不同，这与图6中不同受力状态下截面屈服的分析相一致，因此后续分析将分别从翼缘受拉状态和翼缘受压状态展开．

图8(c)中截面曲率沿墙高的分布是综合考虑受拉钢筋应变分布和受压混凝土应变分布的产物，曲率分布和应变分布具有高度相似性，且基于曲率的塑性铰长度的取值也与基于应变的取值结果基本一致，说明两者具有可替代性．

由图9可知，无论是翼缘受拉状态还是翼缘受压状态，基于曲率的塑性铰长度取值略小于基于应变的取值，而等效塑性铰长度远小于前两者，这是由于塑性铰模型假定等效塑性铰长度内截面塑性曲率相同且均等于截面极限曲率，这实际高估了塑性铰区内的曲率分布，从而低估了塑性铰长度，但2倍的等效塑性铰长度与其余两种方法的取值结果相当．通过与试验破坏区域的对比可知：对于翼缘受拉方向，方法1与方法2得到的塑性铰长度与腹板自由端混凝土竖向裂缝的开裂范围相近；而对于翼缘受压方向，方法1与方法2得到的塑性铰长度与试验实测腹板自由端钢筋的屈服范围相近，这不仅与基于应变的塑性铰长度分析结果相一致，也进一步验证了数值计算结果的准确性．

图9 不同取值方法下塑性铰长度与试验破坏区域的对比

3 塑性铰长度全过程分析

对于钢筋混凝土构件，其塑性铰不是集中于单一截面，而是会随着塑性变形的增大沿构件长度方向扩展至一定范围．塑性铰的扩展主要是由弯矩的增大、弯剪斜裂缝以及纵筋滑移这三方面因素导致的，但由于构件各受力阶段的损伤特征和刚度退化程度的不同，塑性铰长度势必不会随位移的增大而呈线性增长，因此有必要对其在整个受力过程中的变化规律展开研究．

图10给出了T形截面带翼缘剪力墙塑性铰长度随顶点位移的变化曲线，其中初始屈服位移表示最外侧受拉钢筋首次达到屈服应变或受压侧边缘混凝土首次达到峰值应变时对应的位移，而等效屈服位移为采用能量等效法确定出的屈服位移．为了更清楚地阐明不同受力阶段间塑性铰长度的变化机理，图11给出了翼缘受拉方向不同受力阶段下混凝土的应变云图，图12给出了翼缘受压方向不同受力阶段下钢筋的应变云图，云图中将超过钢筋屈服应变和混凝土峰值压应变的区域标注为黑色．

对于翼缘受拉方向，在初始加载阶段(段)，剪力墙处于弹性阶段，直至初始屈服点才在墙肢底部形成塑性铰．初始屈服点后(段)，塑性铰沿墙高方向迅速扩展，在达到等效屈服点时，受压混凝土塑性变形区域已初步形成．在等效屈服点和峰值点间(段)，塑性铰长度增长缓慢，混凝土的损伤更多朝墙体内部发展．峰值点后(段)，塑性铰长度进入二次增长阶段，此阶段腹板自由端混凝土竖向劈裂裂缝加速发展，根部混凝土最终被压溃．整体来看，对于翼缘受拉方向，T形墙的塑性铰长度在塑性阶段呈现先快后慢再快的增长趋势．

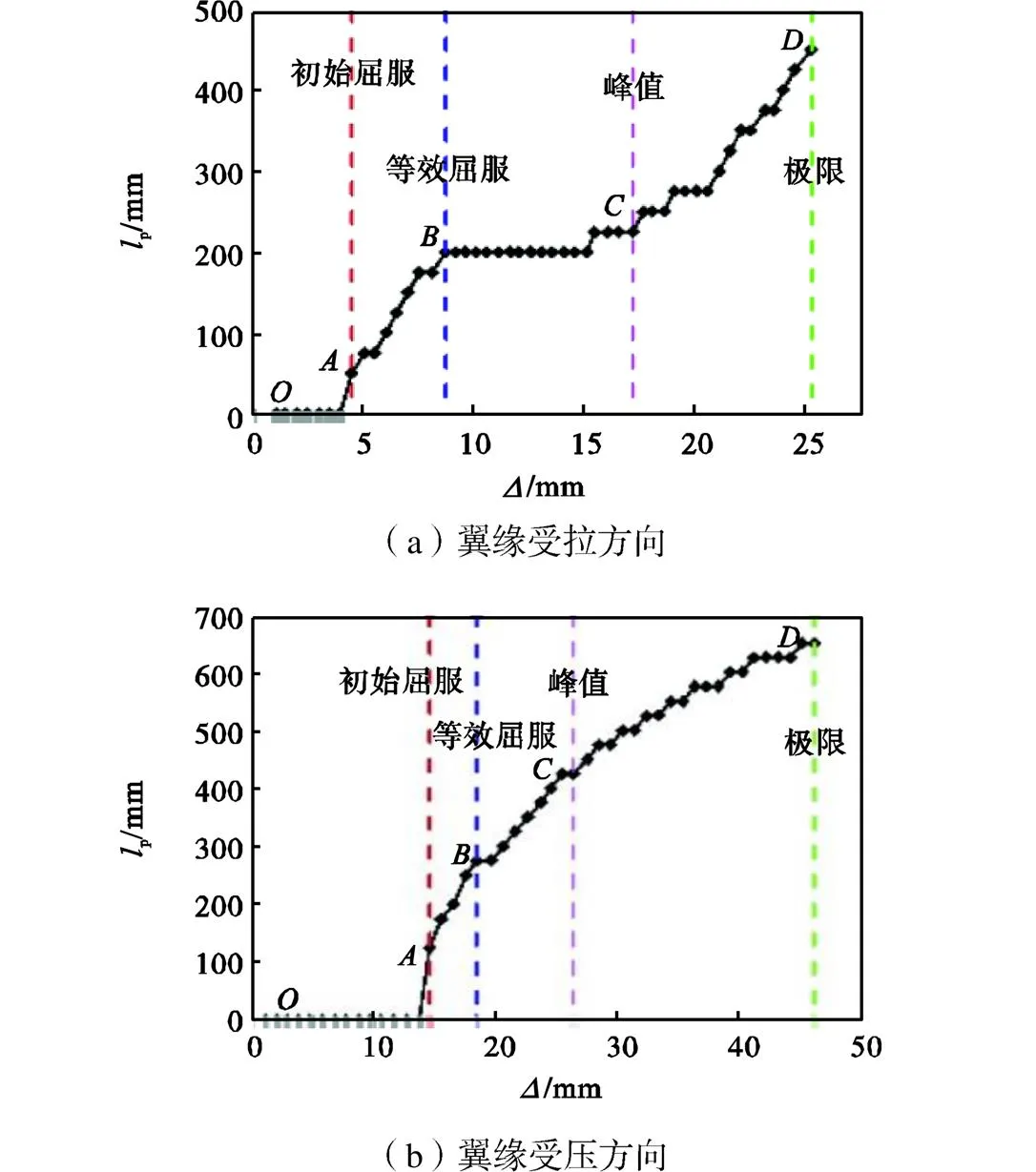
图10 塑性铰长度随加载过程的变化

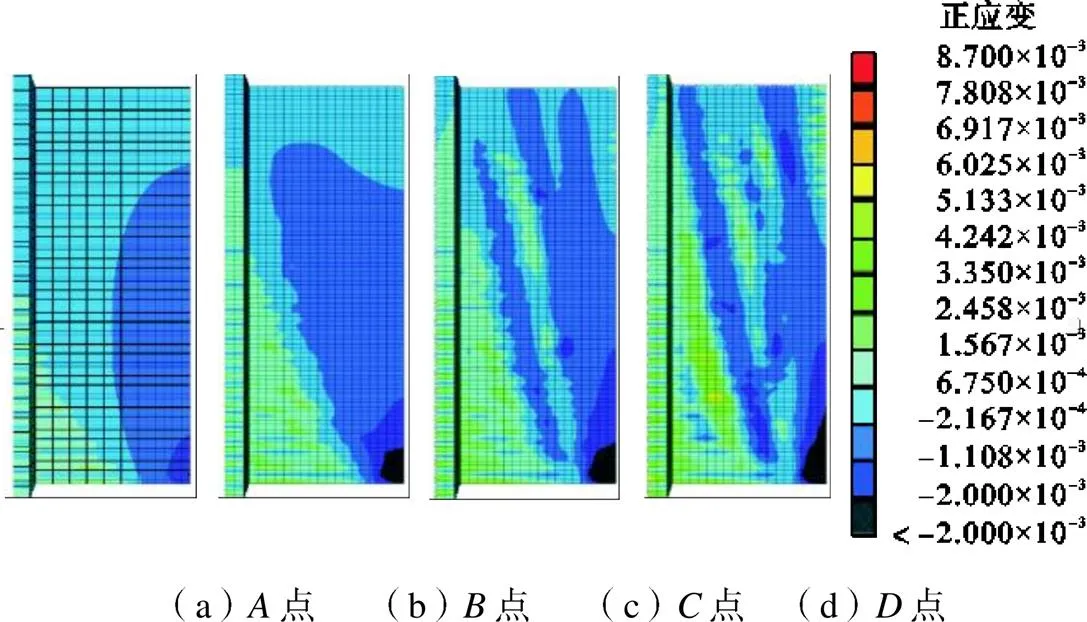
图11 翼缘受拉方向混凝土应变云图

对于翼缘受压方向，剪力墙从初始屈服到峰值荷载阶段，其塑性铰长度的增大较快，而峰值荷载后塑性铰长度的增大略有放缓．整体来看，塑性铰长度的增长速率呈现不断减小的趋势，其随位移的变化曲线近似呈抛物线形式．

虽然塑性铰长度是随加载过程变化的量，但部分学者认为峰值荷载后塑性铰长度的变化幅度较小，加之峰值状态的定义明确且取值简便，因此常取峰值荷载对应的塑性铰长度进行变形能力的估算[4, 10-11]．但上述分析表明，极限状态下的塑性铰长度会超过峰值荷载时的50%，甚至达到2倍之多．因此，采用峰值状态下的塑性铰长度会相当程度地低估构件的极限变形能力．当然这对于基于位移的抗震设计是偏于安全的，但也会造成材料的浪费．因此，对于带翼缘剪力墙这类在达到峰值荷载后塑性铰长度仍有相当增长空间的RC构件，建议采用极限状态下的塑性铰长度进行变形能力计算．以下分析均采用极限状态下的塑性较长度进行分析．

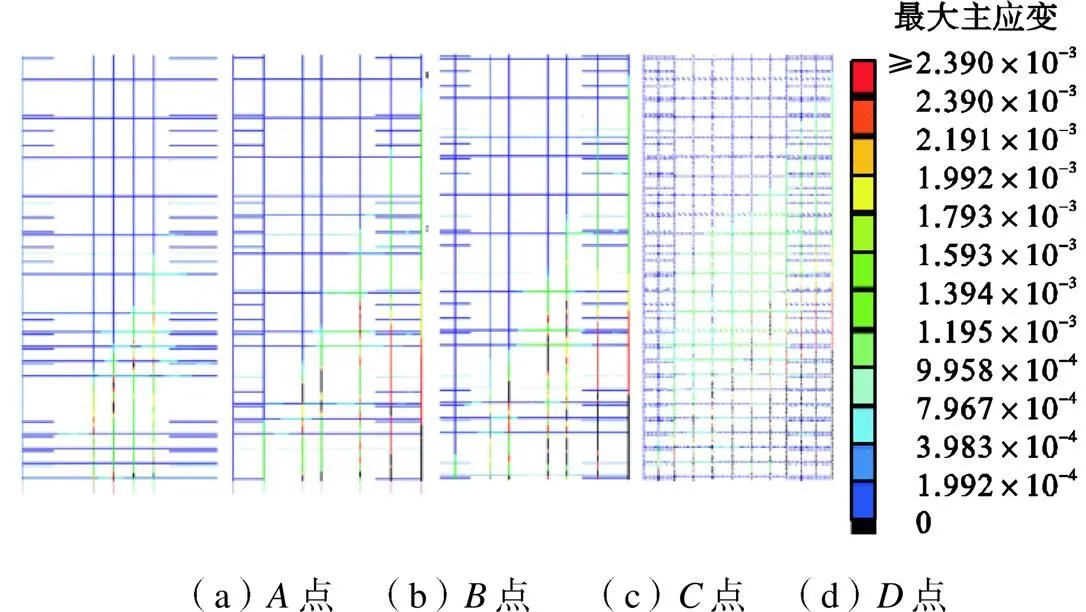
图12 翼缘受拉方向混凝土应变云图

4 塑性铰长度影响因素分析

为了揭示T形截面带翼缘剪力墙塑性铰长度随不同影响因素的变化规律，为建立塑性铰长度计算公式提供数据支撑，需要展开系统全面的塑性铰长度影响因素分析．由于塑性铰长度与抗震性能指标存在关联，因此所选取的影响因素需涵盖影响T形墙抗震性能的关键参数，同时参考已有剪力墙塑性铰长度研究成果，本文选取的影响因素包括轴压比、剪跨比、腹板高度与翼缘宽度比、纵筋配筋率、腹板水平和竖向分布钢筋配筋率、配箍特征值．各因素的变化范围见表1．参数分析时，以试验试件TW-1为基准，每次改变其中一个参数取值，其余参取值保持不变．由于表1中各参数均无量纲，为了合理表述塑性铰长度与各参数的相关关系，将塑性铰长度p除以截面高度w，得到无量纲塑性铰长度系数，＝p/w.以下就塑性铰长度系数随各参数的变化规律展开 讨论．

参数取值的变化对于塑性铰长度的影响，一方面与截面受压区高度相关(图6)，体现在中和轴位置的变化对受拉钢筋应变或受压混凝土应变的影响，进而改变塑性铰长度．具体表现为受压区高度增大时，钢筋拉应变减小，混凝土压应变增大，从而钢筋屈服范围减小，混凝土屈服范围增大，反之亦然．另一方面塑性铰长度的变化也与构件的变形能力(延性)相关，变形能力越好，塑性铰发展越充分，塑性铰长度也越大．塑性铰长度随不同影响因素的变化规律可综合以上两方面因素进行解释．

表1 影响因素及其取值

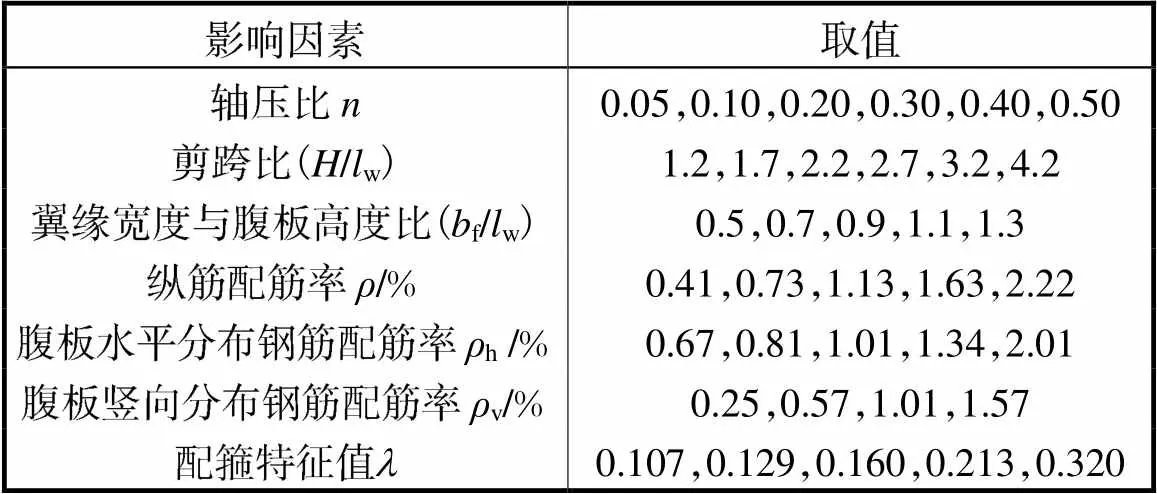
Tab.1 Influentialfactors and their values

4.1 轴压比

图13给出了塑性铰长度随轴压比的变化关系，图中空心符号表示塑性铰长度是由受拉钢筋屈服范围决定的；实心符号表示塑性铰长度是由受压混凝土屈服范围决定的．由图13可知，对于翼缘受拉方向，当轴压比较小时，塑性铰长度是由受拉钢筋的屈服范围决定的，而轴压比超过0.1后，混凝土的屈服范围决定了塑性铰长度，且随着轴压比对的增大，塑性铰长度相应增大．这是因为轴压力的提高会增大截面受压区高度，进而增大了受压边缘混凝土的应变，从而扩大了受压混凝土的屈服范围．对于翼缘受压方向，塑性铰长度均由受拉钢筋的屈服范围决定，同时由于翼缘宽度较大且中和轴位于翼缘内，轴压力的增大对于受压区高度的影响不明显，因而塑性铰长度维持不变．

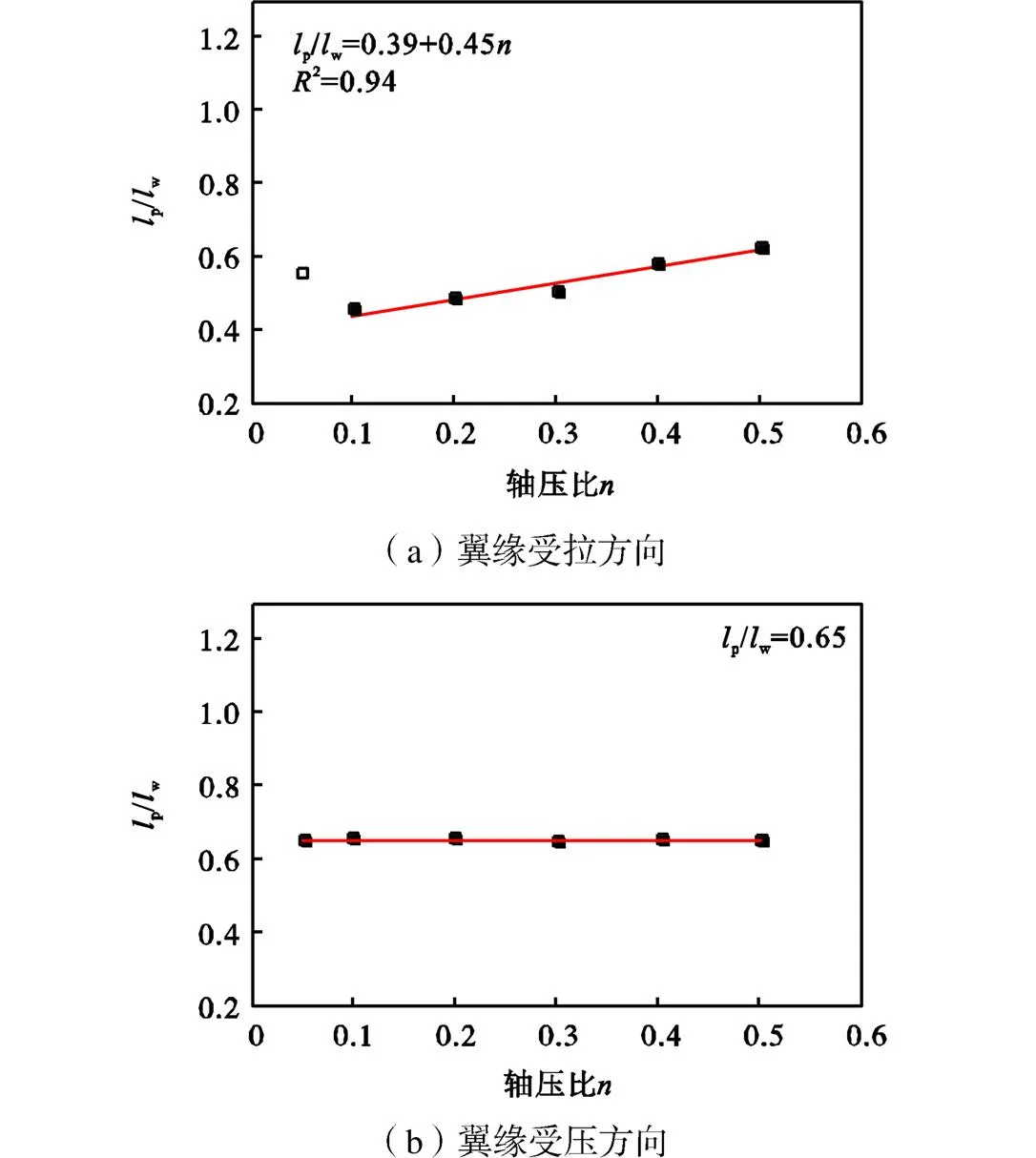
图13 轴压比对塑性铰长度的影响

4.2 剪跨比

剪跨比的变化是通过调整剪力墙高度实现的，墙高依次取1.2m、1.7m、2.2m、2.7m、3.2m和4.2m，相应的剪跨比依次为1.2、1.7、2.2、2.7、3.2和4.2．图14给出了塑性铰长度随剪跨比的变化关系．由图可知，随着剪跨比的增大，T形墙两方向的塑性铰长度均明显增大，变形能力显著增强．此外，翼缘受压方向塑性铰长度随剪跨比的变化幅度大于翼缘受拉方向，这是因为随着剪力墙高度的增大，受拉钢筋的屈服范围近似呈线性增长，而受压混凝土的损伤范围增长较慢．翼缘受压方向塑性铰长度始终由受拉钢筋屈服控制，因而其变化幅度较大；翼缘受拉方向塑性铰长度在剪跨比较小时由受压混凝土屈服控制，但随着剪力墙高度的增大，受拉钢筋的屈服范围超过了受压混凝土，其整体的变化幅度相对较小．

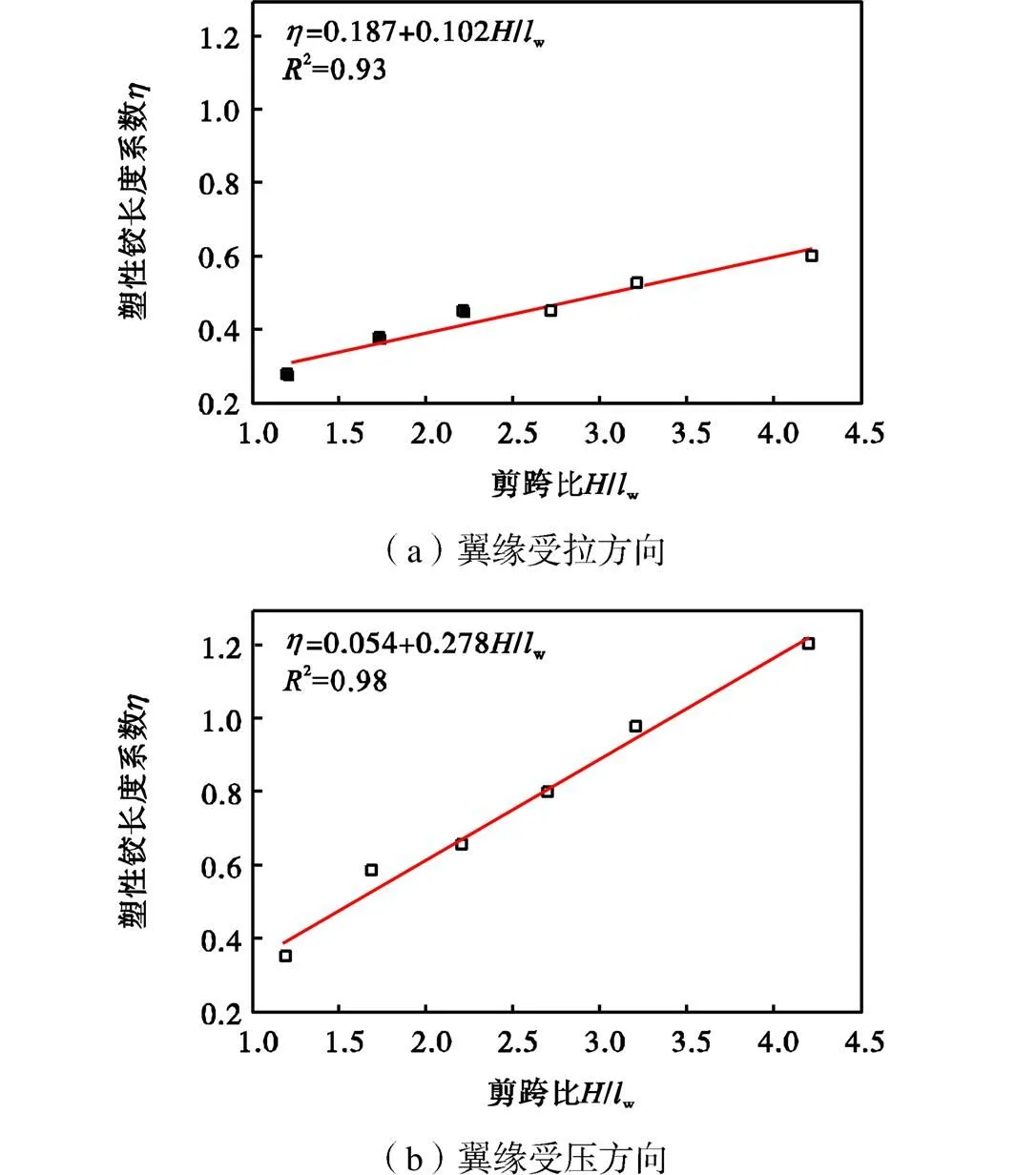
图14 剪跨比对塑性铰长度的影响

4.3 翼缘宽度与腹板高度比

翼缘宽度与腹板高度比的变化是通过改变翼缘宽度实现的，翼缘宽度依次取0.5m、0.7m、0.9m、1.1m和1.3m，相应的翼缘宽度与腹板高度比依次为0.5、0.7、0.9、1.1和1.3．图15给出了塑性铰长度随翼缘宽度与腹板高度比的变化关系．由图5可知，对于翼缘受拉方向，当翼缘宽度大于腹板高度一半时，塑性铰长度由受压混凝土屈服控制，且随着翼缘宽度的增大，塑性铰长度相应减小．分析原因发现：翼缘宽度越大，翼缘受拉方向的截面受压区高度越大，塑性铰长度本应增大，但翼缘宽度增大的同时也使得剪力墙受弯承载力显著增强，在塑性铰长度还未有效发展时剪力墙就已发生脆性剪切破坏，变形能力大幅度减弱，塑性铰长度呈减小的态势．对于翼缘受压方向，塑性铰长度始终由受拉钢筋屈服控制，翼缘宽度的增大减小了截面受压区高度，导致受拉区范围和应变均得到增大，因而塑性铰长度有所增大．

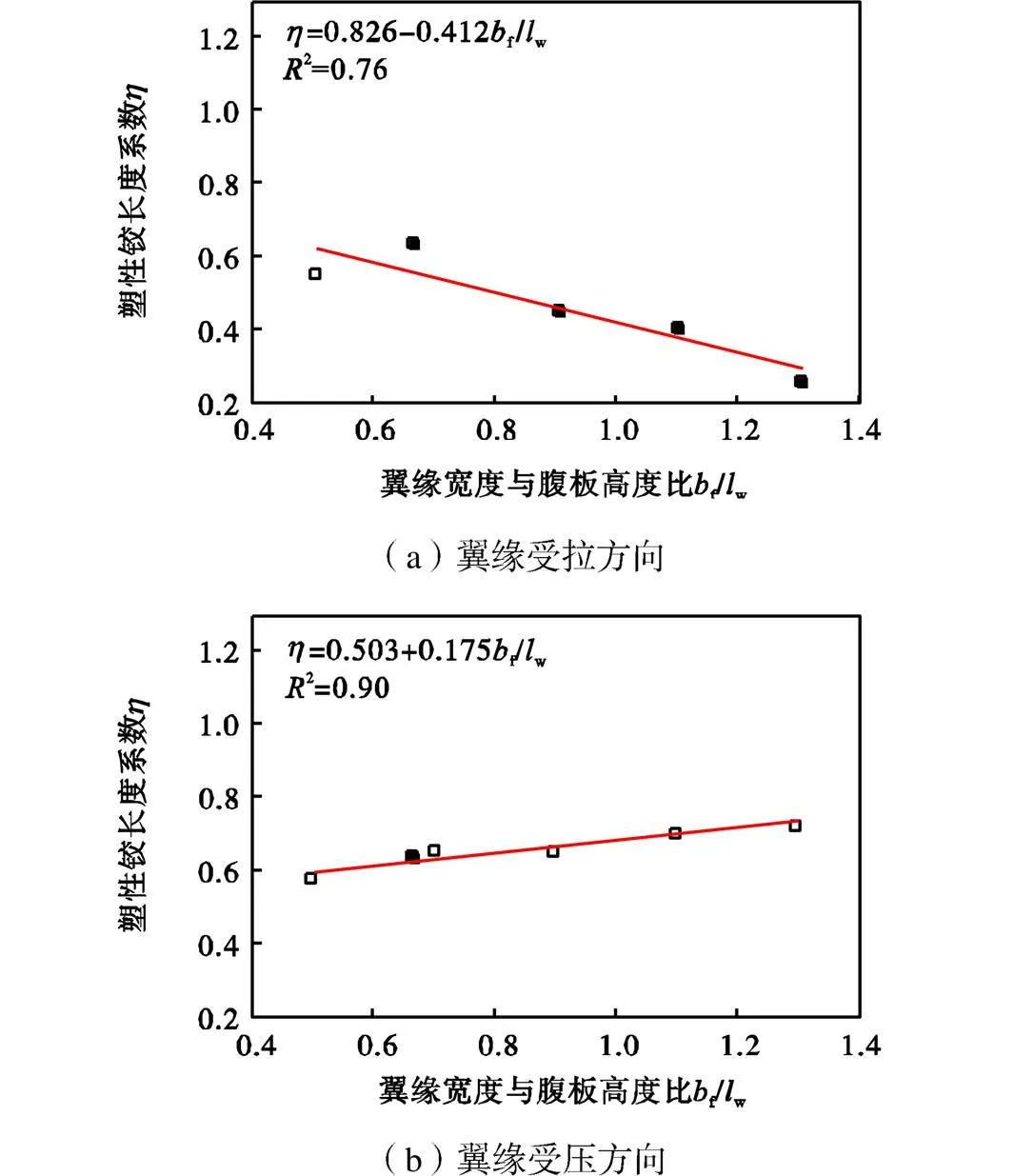
图15 翼缘宽度与腹板高度比对塑性铰长度的影响

4.4 纵筋配筋率

纵筋配筋率的变化是通过调整钢筋直径实现的，纵筋直径依次取6mm、8mm、10mm、12mm、14mm，相应的纵筋配筋率依次为0.41%、0.73%、1.13%、1.63%和2.22%．图16给出了塑性铰长度随纵筋配筋率的变化关系．由图16可知，对于翼缘受拉方向，塑性铰长度基本由受压混凝土屈服控制，且随着纵筋配筋率的增大，塑性铰长度相应增大；对于翼缘受压方向，塑性铰长度均由受拉钢筋屈服控制，且随着纵筋配筋率的增大，塑性铰长度相应减小．虽然纵筋配筋率的提高对于截面受拉区和受压区的应力及其合力均有提高，但就本文所研究T形墙的参数设定和受荷情况而言，受压纵筋离中和轴位置更近，其产生的应力值较小，而受拉区纵筋的应力值较大，提高纵筋配筋率使得受拉区合力增大，从而受压区高度增加，因此塑性铰长度在翼缘受拉方向增大，在翼缘受压方向减小．

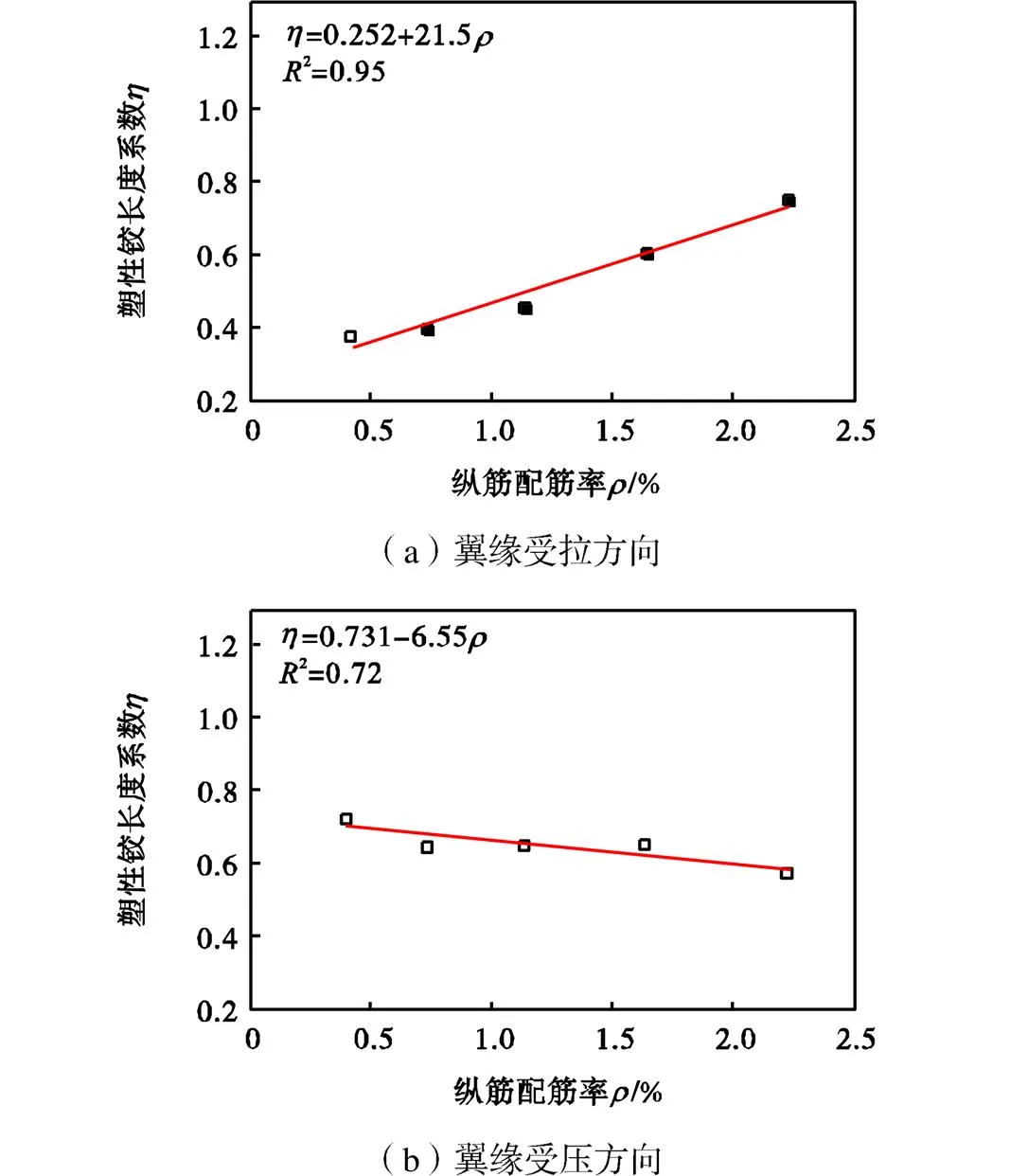
图16 纵筋配筋率对塑性铰长度的影响

4.5 腹板水平分布钢筋配筋率

腹板水平分布钢筋配筋率的变化是通过调整钢筋间距实现的，水平分布筋间距依次取150mm、125mm、100mm、75mm和50mm，相应的配筋率依次为0.67%、0.81%、1.01%、1.34%和2.01%．图17给出了塑性铰长度随腹板水平分布钢筋配筋率的变化关系．由图17可知，在保证破坏模式不改变的前提下，当腹板水平分布钢筋配筋率由0.67%增大到1.34%时，塑性铰长度减小．这是因为增大水平分布钢筋间距(减小配筋率)使得剪切裂缝和剪切变形增大，弯剪耦合作用加剧，导致纵筋和混凝土的正应变增大，因而屈服范围相应增大．而当水平分布钢筋配筋率较大时，增大水平分布钢筋配筋率对剪切效应的影响较小，但可对受压区混凝土形成有效约束，使得混凝土屈服范围增大，因此在水平分布钢筋配筋率由1.34%增大到2.01%时，翼缘受拉方向的塑性铰长度不减反增．对于翼缘受压方向，塑性铰长度同样随着水平分布钢筋配筋率的增大而减小，且其变化程度更为显著，原因在于该方向剪切裂缝数量更多，宽度更大，且剪切变形所占比重更高，但塑性铰长度的减小速率呈不断降低的趋势，其变化曲线呈指数分布．

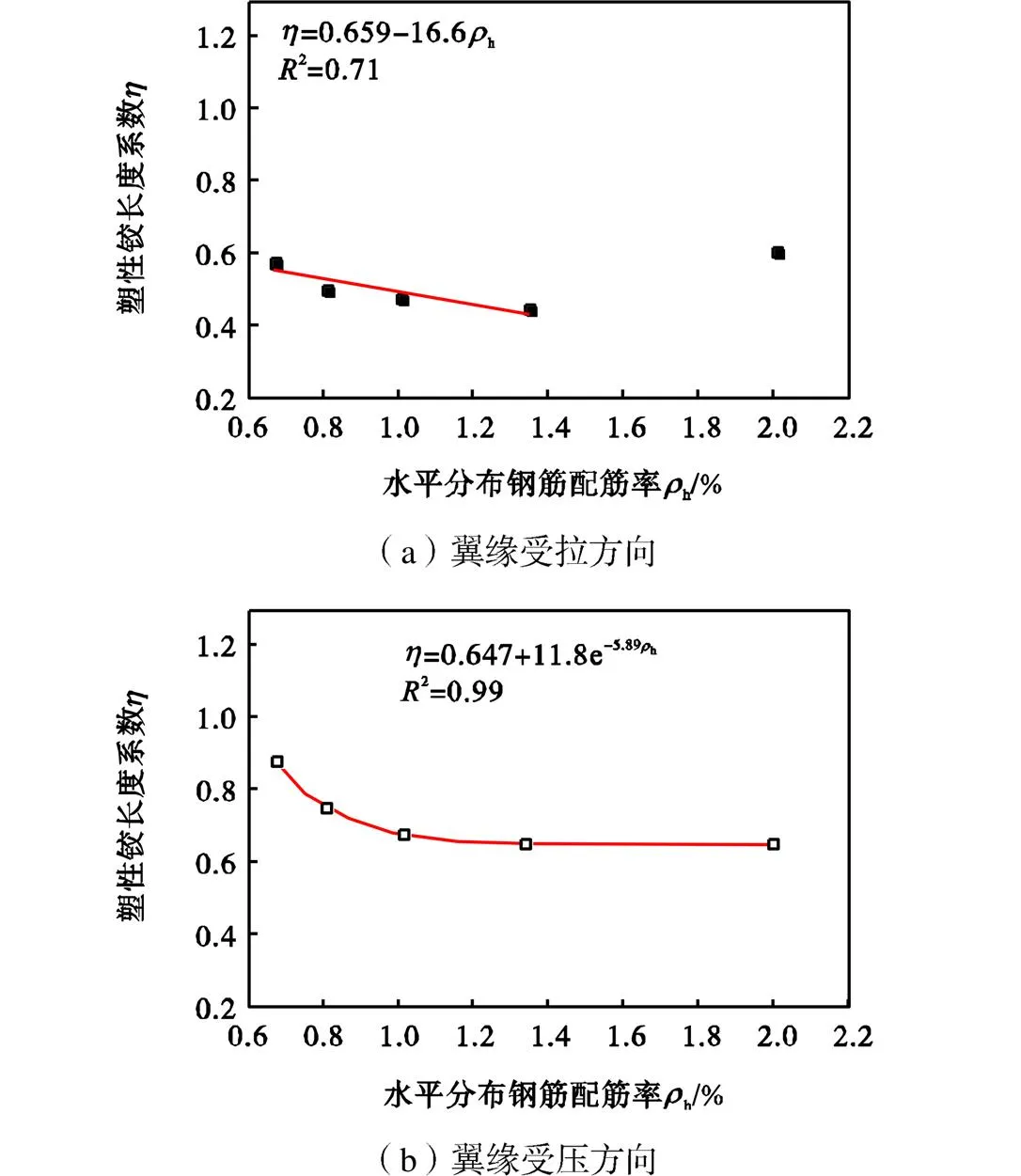
图17 水平分布钢筋配筋率对塑性铰长度的影响

4.6 腹板竖向分布钢筋配筋率

腹板竖向分布钢筋配筋率的变化是通过调整钢筋直径实现的，竖向分布钢筋直径依次取4mm、6mm、8mm和10mm，相应的配筋率依次为0.25%、0.57%、1.01%和1.57%．图18给出了塑性铰长度随腹板竖向分布钢筋配筋率的变化关系．由图18可知，对于翼缘受拉方向，竖向分布钢筋配筋率的提高使得截面受压区高度增大，混凝土屈服范围相应增大．虽然竖向分布钢筋提供的销栓作用可一定程度抑制剪切变形，但对塑性铰长度的影响不明显．对于翼缘受压方向，改变竖向分布钢筋配筋率对于截面受压区高度的影响较小，塑性铰长度保持不变．

4.7 配箍特征值

配箍特征值的变化是通过调整箍筋间距实现的，箍筋间距依次取150mm、125mm、100mm、75mm和50mm，相应的配箍特征值依次为0.107、0.129、0.160、0.213和0.320．图19给出了塑性铰长度随配箍特征值的变化关系．由图19可知，对于翼缘受拉方向，随着配箍特征值的增大，一方面受压区混凝土的合力增大，受压区高度减小，导致受压侧塑性铰长度减小．但另一方面配箍特征值的增大也使得构件变性能力增强，塑性铰发展程度加深，塑性铰长度增大．综合来看，配箍特征值较小时，塑性铰长度由受拉钢筋屈服控制，T形墙在腹板端部较早发生局部压碎破坏，塑性铰长度较小；而配箍特征值较大时，塑性铰长度由受压混凝土屈服控制，构件变形能力较强，塑性较长度较大，塑性铰长度与配箍特征值间没有明确的相关关系．对于翼缘受压方向，箍筋始终未屈服，改变配箍特征值对塑性铰长度基本没有影响．

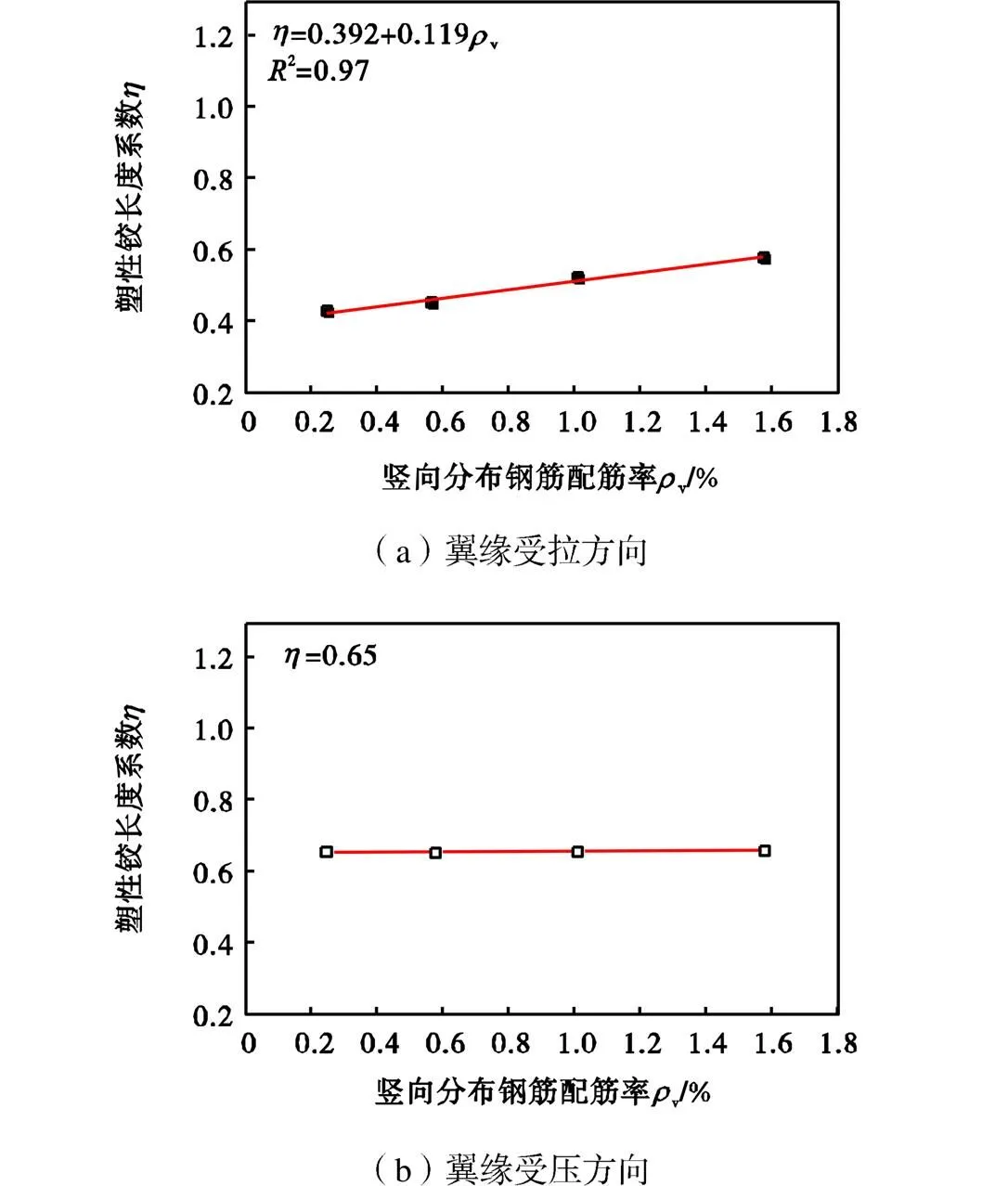
图18 竖向分布钢筋配筋率对塑性铰长度的影响

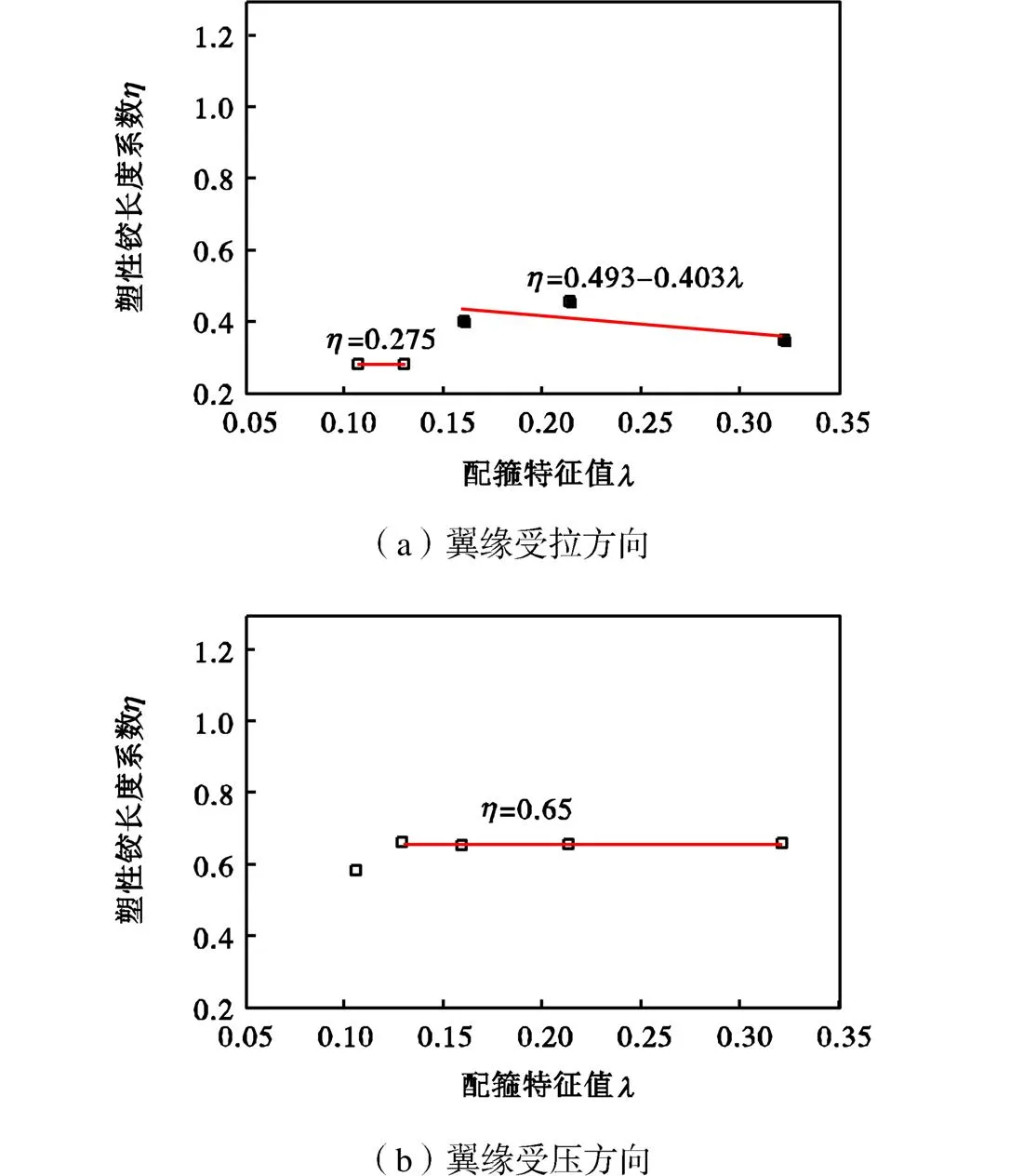
图19 配箍特征值对塑性铰长度的影响

5 塑性铰长度的计算

5.1 简化计算方法

由参数分析可知，影响T形墙翼缘受拉方向塑性铰长度的主要因素包括轴压比、剪跨比、翼缘宽度与腹板高度比以及纵筋配筋率；影响翼缘受压方向塑性铰长度的主要因素包括剪跨比、纵筋配筋率以及腹板水平分布钢筋配筋率．

由单参数回归分析可知，对于翼缘受拉方向，塑性铰长度系数(＝p/w)与各影响因素间近似呈线性关系，因此可采用多元线性函数进行回归，得到翼缘受拉方向塑性铰长度系数计算公式为

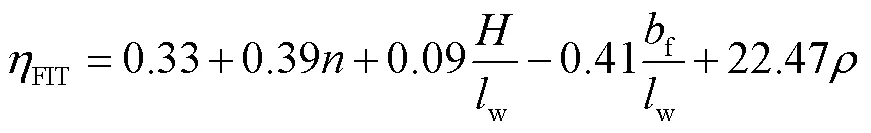
对于翼缘受压方向，塑性铰长度系数与腹板水平分布钢筋配筋率呈指数关系，而与其余影响因素均近似呈线性关系，因此可采用多元线性函数与指数函数的组合进行回归，得到翼缘受压方向塑性铰长度系数计算公式为

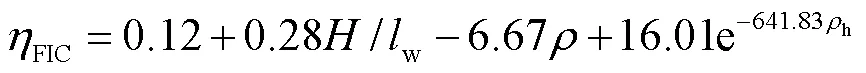
式(6)中h的取值应满足《混凝土结构设计规范》[20]规定的最小配筋率要求(h＞0.25%)，同时应保证剪力墙发生弯曲破坏．图20对比了塑性铰长度系数的公式计算值和有限元模拟值，从两者之比的统计分析结果可以看出，翼缘受压方向的拟合度优于翼缘受拉方向，这是因为不同设计参数下翼缘受拉方向塑性铰长度的决定因素不同，造成数值计算结果具有一定的波动性，而翼缘受压方向塑性铰长度均由受拉钢筋屈服控制，数值计算结果的规律性较好．总体来看，式(5)和式(6)可较为准确地预测T形墙的塑性铰长度系数．

将塑性铰长度系数乘以截面高度w，即可得到T形墙翼缘受拉和翼缘受压方向塑性铰长度的简化计算公式为

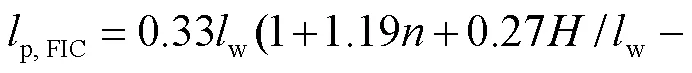
(8)

取塑性铰长度的一半，即可得到用于塑性铰模型计算的等效塑性铰长度．由于回归分析所依据的数值计算结果是基于实体有限元模型而得，其中已考虑了剪切效应的影响，并在所提公式中通过剪跨比来体现，因而上述公式考虑了影响塑性铰长度的两个主要因素(弯矩梯度和剪切效应)．但鉴于数值计算时认为钢筋与混凝土间无相对滑移，对于纵筋滑移的影响并未考虑，因此本文在上述公式的基础上引入考虑纵筋滑移影响的附加项pb，得到修正的等效塑性铰长度计算公式为

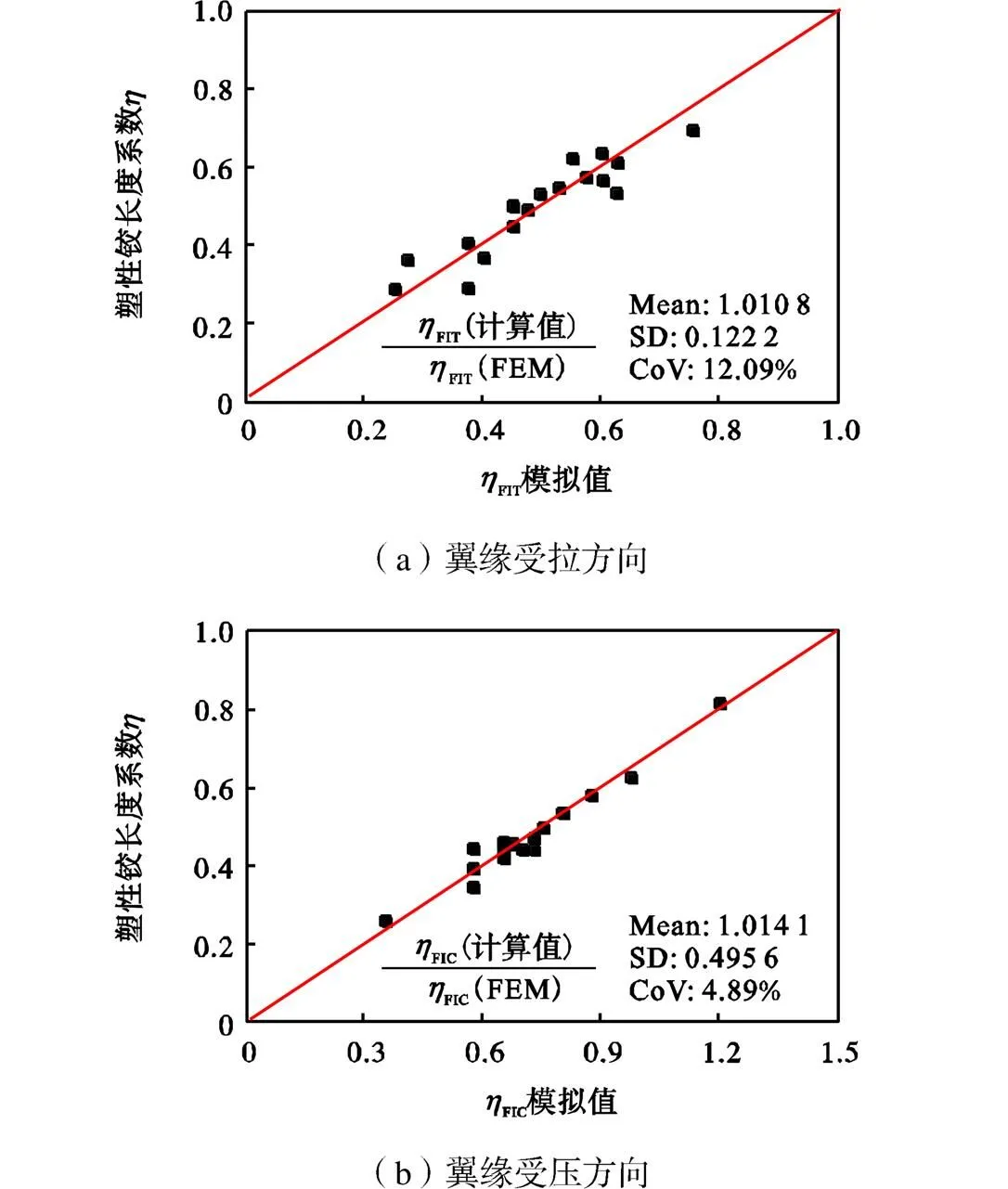
图20 塑性铰长度系数拟合优度检验

附加项pb可采用Paulay等[5]提出的经典表达式

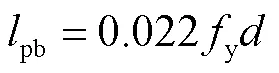
式中y和分别为受拉纵筋的屈服强度和直径．将式(7)、式(8)和式(10)代入式(9)，可得到翼缘受拉和翼缘受压方向等效塑性铰长度计算公式如下：

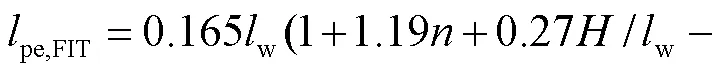
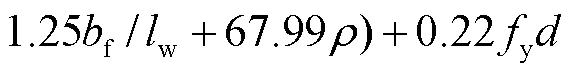
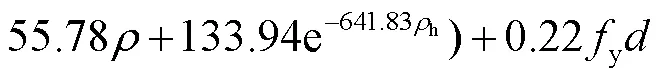
本文提出的带翼缘RC剪力墙塑性较长度计算公式，不仅综合考虑了弯矩梯度、剪切效应和纵筋滑移的贡献，也将翼缘受拉方向和翼缘受压方向进行了区分，更符合T形截面剪力墙的受力变形特征．此外，本文公式考虑了影响T形墙塑性铰长度的主要因素，公式形式也相对简单，确保了公式的准确性和简便性，便于指导工程设计．

5.2 试验验证

针对文献[12，21-24]中一系列发生弯曲破坏的T形墙和L形墙试验试件，根据其实测的极限弯曲位移利用式(4)反算出等效塑性铰长度pe,exp，并与本文预测公式的计算结果pe,pre进行对比，试验试件参数及对比结果见表2．

表2 等效塑性铰长度试验值与计算值对比

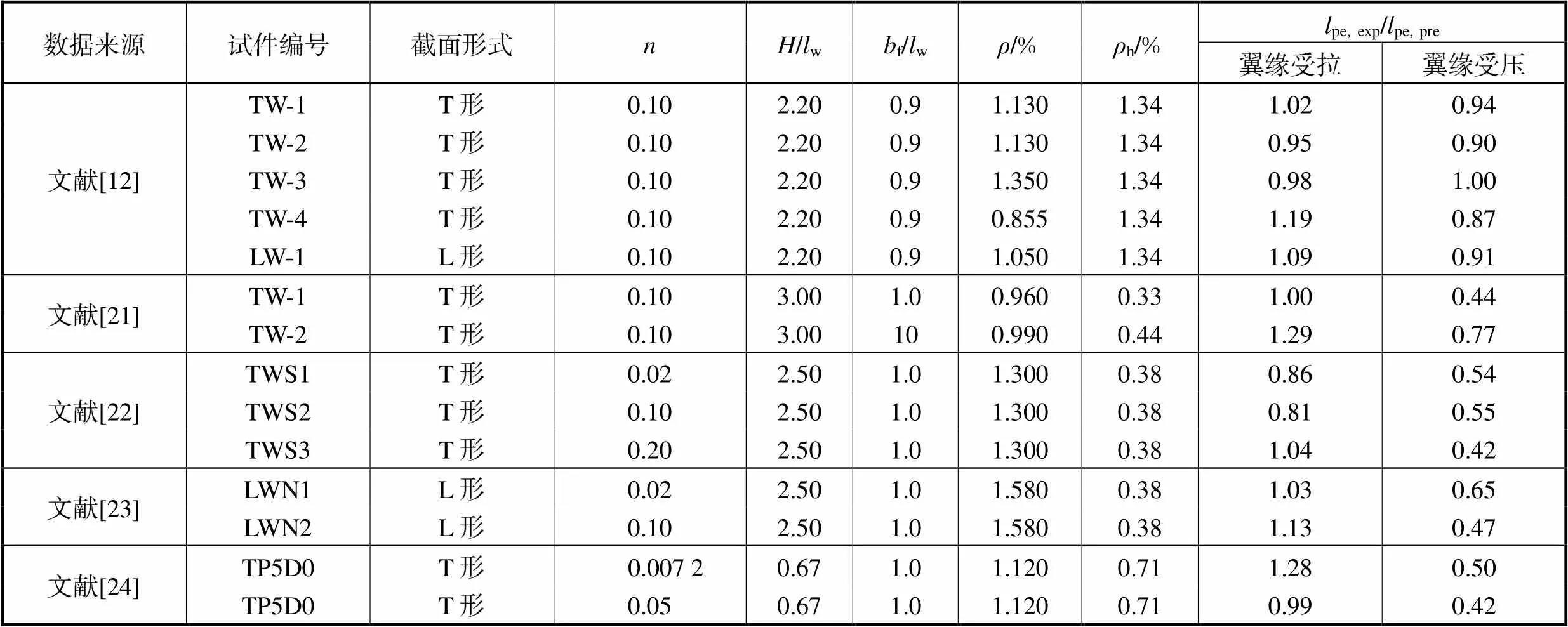
Tab.2 Comparison of equivalent plastic hinge length between experimental and calculated results

由表2可以看出，等效塑性铰长度的计算值与试验值的差异基本在10%以内，且试验值大多小于计算值．这是因为塑性铰模型假定塑性铰区内曲率呈线性分布，等效塑性铰长度取为实际塑性铰长度的一半，但塑性区域内曲率更接近于指数分布，基于塑性转角等效前后相同的原则，等效塑性铰长度应小于实际塑性铰长度的一半，因此本文模型一定程度高估了等效塑性铰长度．此外，文献[21-24]翼缘受压方向等效塑性铰长度的计算结果远超试验值，试验值与计算值之比约为0.5．造成此差异的原因在于这几组试验均采用推拉等幅加载模式，但T形墙和L形墙截面的不对称性导致其在翼缘受拉和翼缘受压方向的极限变形能力存在显著差异．在翼缘受拉方向破坏时，翼缘受压方向还未达到承载力极限状态，更未能达到计算设定的极限状态，因此计算出的等效塑性铰长度远大于试验值．总体来看，本文提出的塑性铰长度计算公式不仅能准确计算出T形墙的塑性变形区域，对于L形墙也同样适用，可为带翼缘剪力墙基于位移的抗震设计提供参考．

6 结 论

(1) T形截面带翼缘RC剪力墙在翼缘受拉状态和翼缘受压状态下塑性铰长度不仅取值大小不同，且取值的决定因素也不同，翼缘受压方向的塑性铰长度普遍大于翼缘受拉方向．

(2) 对于翼缘受拉方向，T形墙的塑性铰长度在塑性阶段呈现先快后慢再快的增长趋势；而对于翼缘受压方向，塑性铰长度的增长速率呈现不断减小的趋势，极限状态下的塑性铰长度会超过峰值荷载时的50%，建议采用极限状态下的塑性铰长度进行变形能力计算．

(3) 影响T形墙翼缘受拉方向塑性铰长度的主要因素包括轴压比、剪跨比、翼缘宽度与腹板高度比以及纵筋配筋率，其中轴压比、剪跨比以及纵筋配筋率与塑性铰长度正线性相关，而翼缘宽度与腹板高度比与塑性铰长度负线性相关．影响翼缘受压方向塑性铰长度的主要因素包括剪跨比、纵筋配筋率以及腹板水平分布钢筋配筋率，塑性铰长度随着剪跨比的增大而线性增大，随着纵筋配筋率和腹板水平分布钢筋配筋率的增大而减小，且呈明显的非线性关系．

(4) 基于数值计算结果，提出了多参数影响下T形墙塑性铰长度简化计算公式．通过与试验结果的比对，验证了计算公式的准确性．所提公式不仅综合考虑了弯矩梯度、剪切效应和纵筋滑移的贡献，也将翼缘受拉方向和翼缘受压方向进行了区分，更符合T形墙的受力变形特征，且亦可应用于L形墙，研究成果可为带翼缘剪力墙基于位移的抗震设计和性能评估提供参考．

［1］ 于敬海，丁永君，谢 剑，等. 高强钢筋高强混凝土双肢剪力墙抗震性能试验[J]. 天津大学学报(自然科学与工程技术版)，2017，50(2)：181-187.

Yu Jinghai，Ding Yongjun，Xie Jian，et al. Experiment on seismic behavior of high strength reinforced concrete coupled shear wall[J]. Journal of Tianjin University(Science and Technology)，2017，50(2)：181-187(in Chinese).

［2］ 杨 坤，史庆轩，赵均海. 高强箍筋高强混凝土柱的塑性铰长度[J]. 工程力学，2013，30(2)：254-259.

Yang Kun，Shi Qingxuan，Zhao Junhai. Plastic hinge length of high-strength concrete columns confined by high-strength stirrups[J]. Engineering Mechanics，2013，30(2)：254-259(in Chinese).

［3］ 李振宝，张 岩，解咏平，等. 钢筋混凝土柱塑性铰长度尺寸效应研究[J]. 北京工业大学学报，2014，40(9)：1334-1340.

Li Zhenbao，Zhang Yan，Xie Yongping，et al. Size effect on plastic hinge length of reinforced concrete columns[J]. Journal of Beijing University of Technology，2014，40(9)：1334-1340(in Chinese).

［4］ 仇建磊，张艳青，贡金鑫. 钢筋混凝土柱等效塑性铰长度计算研究[J]. 大连理工大学学报，2017，37(6)：38-45.

Qiu Jianlei，Zhang Yanqing，Gong Jinxin. Study of evaluation of equivalent plastic hinge length of reinforced concrete columns[J]. Journal of Dalian University of Technology，2017，37(6)：38-45(in Chinese).

［5］ Paulay T，Priestley M J N. Stability of ductile structural walls [J]. ACI Structural Journal，1993，90(4)：385-392.

［6］ Bohl A，Adebar P. Plastic hinge lengths in high-rise concrete shear walls[J]. ACI Structural Journal，2011，108(2)：148-157.

［7］ Kazaz İ. Analytical study on plastic hinge length of structural walls[J]. Journal of Structure Engineering，2013，139(11)：1938-1950.

［8］ 张 松，吕新林，章红梅. 钢筋混凝土剪力墙构件极限位移的计算方法及试验研究[J]. 土木工程学报，2009，42(4)：10-16.

Zhang Song，Lü Xinlin，Zhang Hongmei. Experimental and analytical studies on the ultimate displacement of RC shear walls[J]. China Civil Engineering Journal，2009，42(4)：10-16(in Chinese).

［9］ 王义俊，汪梦甫. 钢筋混凝土剪力墙塑性铰长度计算模型研究[J]. 工业建筑，2016，46(5)：80-85.

Wang Yijun，Wang Mengfu. Study on calculation model of plastic hinge length of reinforced concrete shear walls [J]. Industrial Construction，2016，46(5)：80-85(in Chinese).

［10］ 黄 远，洪露露，万雄伟，等. 钢筋混凝土剪力墙塑性铰长度[J]. 地震工程与工程振动，2019，39(2)：79-88.

Huang Yuan，Hong Lulu，Wan Xiongwei，et al. Plastic hinge length of reinforced concrete shear wall[J]. Earthquake Engineering and Engineering Dynamics，2019，39(2)：79-88(in Chinese).

［11］ Mun J H，Yang K H. Plastic hinge length of reinforced concrete slender shear walls[J]. Magazine of Concrete Research，2015，67(8)：414-429.

［12］ 史庆轩，王 斌，何伟锋，等. 带翼缘钢筋混凝土剪力墙抗震性能试验研究[J]. 建筑结构学报，2017，38(1)：106-115.

Shi Qingxuan，Wang Bin，He Weifeng，et al. Experimental research on seismic behavior of reinforced concrete shear walls with flange[J]. Journal of Building Structures，2017，38(1)：106-115(in Chinese).

［13］ 王 斌，史庆轩，蔡文哲. 带翼缘剪力墙截面曲率分析及延性的计算[J]. 工程力学，2019，36(12)：165-176.

Wang Bin，Shi Qingxuan，Cai Wenzhe. Curvature analysis and ductility calculation of flanged shear wall[J]. Engineering Mechanics，2019，36(12)：165-176(in Chinese).

［14］ Bafti F G，Mortezaei A，Kheyroddin A. The length of plastic hinge area in the flanged reinforced concrete shear walls subjected to earthquake ground motions[J]. Structural Engineering and Mechanics，2019，69(6)：651-665.

［15］ Hoult R D，Goldsworthy H M，Lumantarna E. Plastic hinge analysis for lightly reinforced and unconfined con-crete structural walls[J]. Bulletin of Earthquake Engineering，2018，16：4825-4860.

［16］ Sanez L P. Discussion of equation for the stress-strain curve of concrete by Desayi and Krishnan[J]. ACI Structural Journal，1964，61(9)：1229-1235.

［17］ 聂建国，王宇航. ABAQUS中混凝土本构模型用于模拟结构静力行为的比较研究[J]. 工程力学，2013，30(4)：59-67.

Nie Jianguo，Wang Yuhang. Comparison study of constitutive model of concrete in ABAQUS static analysis of structures[J]. Engineering Mechanics，2013，30(4)：59-67(in Chinese).

［18］ Model Code 90 CEB-FIP[S]. Lausanne：Mai，1993.

［19］ 余玉洁，赵凤涛，郭风琪. 钢管混凝土柱-横肋波纹板剪力墙抗侧性能分析[J]. 天津大学学报(自然科学与工程技术版)，2020，53(12)：1243-1253.

Yu Yujie，Zhao Fengtao，Guo Fengqi. Analysis of lateral resisting behavior of horizontally corrugated steel plate shear wall with concrete-filled steel tube frame[J]. Journal of Tianjin University(Science and Technol-ogy)，2020，53(12)：1243-1253(in Chinese).

［20］ GB 50010—2010 混凝土结构设计规范[S]. 北京：中国建筑工业出版社，2010.

GB 50010—2010 Code for Design of Concrete Structures[S]. Beijing：China Architecture & Building Press，2010(in Chinese).

［21］ Thomsen J H，Wallace，J W. Displacement-based design of slender reinforced concrete structural walls—Experimental verification[J]. Journal of Structure Engineering，2004，130(4)：618-630.

［22］ Zhang Z，Li B. Seismic performance assessment of slender T-shaped reinforced concrete walls[J]. Journal of Earthquake Engineering，2016，20：1342-1369.

［23］ Zhang Z，Li B. Seismic performance of L-shaped RC walls sustaining Unsymmetrical bending[J]. Structural Engineering and Mechanics，2021，78(3)：269-280.

［24］ Ma J，Zhang Z，Li B. Experimental assessment of T-shaped reinforced concrete squat walls[J]. ACI Structural Journal，2018，115(3)：621-634.

Research on Plastic Hinge Length of RC Shear Walls with Flange

Wang Bin1, 2，Shi Qingxuan1, 2，Wu Mengzhen1

(1. School of Civil Engineering，Xi’an University of Architecture & Technology，Xi’an 710055，China；2. Key Laboratory of Structural Engineering and Seismic Resistance，Ministry of Education(XAUAT)，Xi’an 710055，China)

To meet architectural requirements，rectangular walls arranged in orthogonal directions are commonly connected to form flanged shear walls with different section types. The T-shaped shear wall，as the most typical combination form of wall segments，demonstrates different deformation performances and plastic hinge lengths under various loading directions due to the asymmetry of its cross section. To reveal the formation and the development mechanism of the plastic hinge of reinforced concrete(RC)shear walls with flange，a refined finite element analysis model for the T-shaped RC shear wall was established. Based on the verified model，the method to determine the plastic hinge length of the T-shaped RC wall was defined by analyzing the distributions of strain and curvature along the wall height. The variation of the plastic hinge length over the whole loading process was then analyzed. Combined with the damage mechanism and sectional strain distribution of the T-shaped wall，the influence of different design parameters on the plastic hinge length was elaborated. Results show that the plastic hinge length of the T-shaped wall under the flange-in-tension loading is mainly determined by the crushing range of compressive concrete. In addition，the derived value is relatively small，showing an initial growth trend of fast，then slow，and finally fast. For the flange-in-compression case，the plastic hinge length is completely determined by the yielding range of the tensile reinforcement，and the growth rate shows a decreasing trend. Based on parametric analysis results，simplified formulas for calculating the plastic hinge length of the T-shaped wall were proposed，which takes into account the contribution of the moment gradient，shear effect，and longitudinal bar slippage. The accuracy of the simplified formulas was verified by a comparison with experimental results. The proposed formulas conform to the deformation characteristics of the T-shaped walls and can also be applied to L-shaped walls. Research results can provide references for the deformation-based seismic design and the performance evaluation of RC shear walls with flange.

reinforced concrete；T-shaped wall；finite element analysis；plastic hinge length；simplified calculation

10.11784/tdxbz202108022

TU398

A

0493-2137(2022)08-0848-14

2021-08-10；

2021-10-08.

王 斌（1988—  ），男，博士，副教授.Email：m_bigm@tju.edu.cn

王 斌，wangbin@xauat.edu.cn.

国家自然科学基金资助项目(51808435，51878540)；陕西省高校科协青年人才托举计划资助项目(20190419).

the National Natural Science Foundation of China(No. 51808435，No. 51878540)，the Young Talent Fund of University Association for Science and Technology in Shaanxi Province(No. 20190419).

(责任编辑：金顺爱)