基于噪声容错UWB定位的高程越界检测算法研究

吴 勇，宋哲书，嵇友晴，陈瑜洁，顾德扬，陈 蕾,3

(1.江苏省送变电有限公司，江苏 南京 211106;2.南京邮电大学 计算机学院，江苏 南京 210023;3.江苏省大数据安全与智能处理重点实验室，江苏 南京 210003)

0 引 言

近年来，随着国民经济的快速发展和人民生活水平的不断提高，一些老旧变电站不再能满足人民生产生活的用电需求，对老旧变电站进行技术改造和扩建增容势在必行[1]。然而，老旧变电站改扩建施工不同于常规的民用建筑工程施工，变电站内部分布众多的电气设备和电力电缆，而且改扩建施工时变电站不允许停止运行，否则不能正常供电， 最终给人民财产造成重大损失。因此，在老旧变电站改扩建过程中，邻近带电设施的施工区域会成为高危区域，威胁着施工人员的生命安全。为了防止施工过程中人员机具发生触电危险，施工位置通常要与高压设施间隔一段安全距离。传统方法通常采用人工搭建物理围栏的方式进行安全区域划分，然而该方法耗时耗力且无法做到智能预警，更重要的是由于物理围栏的高程限制无法检测施工人员机具的高空越界违章行为，从而给变电站改扩建施工带来重大安全隐患。

为了克服上述缺陷，该文提出一种超宽带虚拟电子围栏(ultra wide-band based virtual electronic fence，UWB-VEF)方案来替代传统的物理围栏，该电子围栏方案之所以选用UWB定位技术，是因为与其他定位技术如GPS定位[2]、Wifi定位[3]、视觉定位[4]、激光雷达定位[5]等技术相比，UWB定位技术兼顾了定位精度高和安装部署简单的双重优点[6]。本质上，UWB技术是一种基于测距的无线定位技术，其定位精度依赖于节点间距离信息的完备和准确程度[7]。然而，在实际的变电站改扩建过程中，由于变电站需带电正常运行，施工区域不可避免会受到周边邻近区域的电磁干扰，这会较大程度影响UWB节点对施工人员机具位置信息的采集精度；此外由于变电站内电气设备众多，UWB节点间的交互通信也极易受到障碍物的遮挡，导致节点间距离信息的缺失。因此，设计一种复杂环境下的超宽带噪声容错定位算法就成了超宽带虚拟电子围栏(UWB-VEF)能否实际应用于变电站改扩建施工的关键挑战。为此，进一步提出了一种基于混合指数幂分布的噪声容错超宽带定位(mixture of exponential power distribution based noise-tolerant UWB localization，MoEP-NULoC)方法，该方法一方面通过低秩矩阵分解技术补全欧氏距离矩阵[8]，另一方面引入混合指数幂分布拟合测距过程中不可预知的复杂噪声，最后采用四点定位法计算出施工人员/机具的位置信息，从而提高了定位精度。

1 相关工作

在本节中，主要介绍相关的虚拟电子围栏以及无线定位技术。

1.1 虚拟电子围栏

近年来，虚拟电子围栏技术在各类工程施工中逐步得到推广应用。常见的虚拟电子围栏技术有脉冲式电子围栏、红外电子围栏、智能脉冲式电子围栏、张力式电子围栏等。脉冲式电子围栏主要由脉冲主机和前端围栏两部分组成，脉冲主机会发出高压低频正脉冲和高压负脉冲，控制在一定能量内的脉冲的能量会使触碰到围栏的人有强烈刺痛感，从而起到阻碍的作用。但是此方法可能会对人体造成不同程度的精神和身体伤害。为了解决以上安全问题，红外对射产品进入市场。红外电子围栏由发射端和接收端两部分组成，接收端接收发射端发射的红外光束，每段红外光束衔接就形成了保护网，当红外光束被阻断，接收端就会输出报警信号。但是，只要光束被挡，即使不是因为人员闯入，也会发生报警，所以这种电子围栏具有高误报率。智能脉冲式电子围栏和张力式电子围栏的推出解决了脉冲式围栏的不足。虽然这两种电子围栏很好地解决了安全问题，且在一般的工程施工场景下具有较低的误报率，但是这两种电子围栏均需要铺设复杂的设备，极易损坏且难以维护，不能很好地适用于变电站改扩建应用场景。为了弥补上述缺陷，该文提出一种面向变电站改扩建施工的超宽带(UWB)虚拟电子围栏方案。UWB作为新兴的无线通信技术，具有低发射功率、低功耗、低成本的特征,且其空间传输容量大，传输速率快，安全性高，在环境监测、智能交通等领域应用广泛[9-11]。

1.2 无线定位技术

目前，无线定位技术通常分为两类[12]：基于测距的定位[13]及距离无关的定位[14]。基于测距的定位算法，例如RSSI、TOA、TDOA等，可以实现更精确的定位，但是计算和通信成本相对较大，并且需要一定的硬件支持。距离无关的定位方法依赖的外部硬件设施少并且消耗能量较少，但只能实现粗粒度定位，通常适用于不需要高精度的应用。

基于测距的无线定位技术通常基于一个假设，即节点间的欧氏距离是完备且准确的。然而，在实际的变电站改扩建过程中，施工区域会不可避免地受到环境噪声的干扰，UWB节点间的交互通信也极易受到障碍物的遮挡，导致节点间距离信息的缺失和失真，这在很大程度上影响着UWB定位的精度。为了解决节点间距离信息缺失及失真的问题，诸多学者对此展开了研究。基于欧氏距离矩阵的内在低秩性，Feng等人[15]首先将矩阵补全(matrix completion，MC)引入到无线传感器网络节点定位领域，利用矩阵补全有效解决了部分节点间距离缺失的问题，并设计了相应的优化算法对其进行求解。但是，他们的工作局限于将节点间测距测量中存在的误差假设为高斯形式的噪声，而忽略了由节点硬件故障、多径传输等导致的一些未知复杂噪声的存在。Cai等人[16]提出了矩阵补全的奇异值阈值算法(a singular value thresholding algorithm，SVT),但是该算法的局限性在于仅能处理无噪声的情况，当距离矩阵包含稀疏的野值噪声时，该算法的性能会大幅下降。肖等人[17]将由硬件故障等因素造成的异常值假设为野值噪声，并引入L1范数正则化技术对其进行平滑，基于此提出了一种抗异常干扰的无线传感器网络节点定位算法，有效提高了节点定位精度。然而，实际的定位系统运行时其环境十分复杂，将节点测距信息中存在的误差预设为高斯噪声和野值噪声过于理想，不合实际。孟等人[18]提出了一种循环加权中值方法(cyclic weighted median method，CWM)，但是L1范数只适用于拟合拉普拉斯噪声，并不能很好地拟合实际中的未知复杂噪声。Liu等人[19]针对测距信息中可能存在的连续误差，采用L21范数对其进行处理，构建了一种基于线性Bregman迭代的矩阵补全模型，并以此为基础设计了一种定位算法。但其工作仍然局限于预设节点测距误差为已知的噪声类型，不符合实际情况。

2 超宽带虚拟电子围栏(UWB-VEF)方案

为了满足变电站改扩建施工中高空越界违章检测的实际需求，提出了超宽带虚拟电子围栏(UWB-VEF)方案。该方案包括以下三个步骤：超宽带(UWB)节点部署、施工安全区域设置、施工人员/机具越界违章行为检测。

Step1：超宽带(UWB)节点部署。

(1)设立定位基站。定位基站设立时要尽量保证基站不共面，在基站架设的时候，需要特别拉开z轴的高度差，以确保在z轴上的精确度。以户内变电站为例，一般选择墙角为原点，两个墙面分设为x轴和y轴，墙面相交线为z轴，此坐标系作为后续标签模块定位坐标的参考坐标系。

(2)设立锚节点。在定位基站中选定合适的节点作为锚节点。在变电站三维定位中，应至少设立四个锚节点，以便根据锚节点来定位未知节点。

(3)设立人员/机具标签。场内施工人员及机具均配备UWB定位标签，以实时计算出施工人员及机具的三维坐标位置。

Step2：施工安全区域设置。

根据变电站改扩建施工的实际情况确定出施工安全区域，在设定的安全区域周围安放数个UWB结点，保证相邻节点的连线形成的多边形覆盖全部安全区域，其所形成的不规则多边形即为超宽带虚拟电子围栏。施工安全区域示意图如图1所示，其中三角形表示安放的UWB节点，z=H平面表示最高的作业高度，超过此高度则会触碰高空的高压线发生触电危险，xOy平面内三角形连线围成的多边形区域即为变电站改扩建安全施工区域，五角星①表示处于安全区域的地面施工作业人员/机具，五角星②表示处于安全区域的高空施工作业人员/机具，五角星③表示处于安全区域外的施工作业人员/机具。

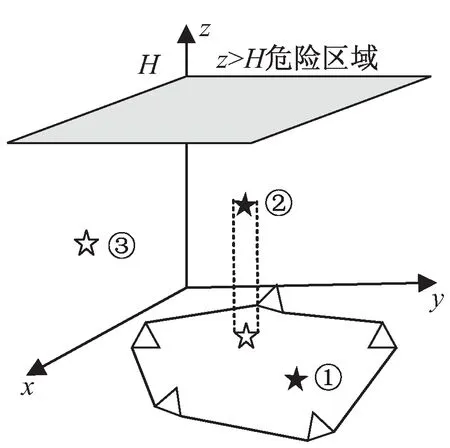
图1 施工危险区域示意图

Step3：施工人员/机具越界违章行为检测。

对于施工人员/机具的越界违章行为检测，主要分为地面施工人员/机具的越界违章检测以及高空施工人员/机具的越界违章检测。为简便起见，下文仅以施工人员为例进行讨论。

对于地面施工人员，检测其是否步入危险区域，只需直接判断施工人员是否位于UWB节点连线围成的多边形内；对于高空作业人员而言，首先要判断作业人员是否有高空触电危险(即判断施工人员所在的垂直高度是否超过该区域最大高度限制H)，其次将高空作业人员的位置映射至xOy平面，然后再判断映射至地面的人员位置是否位于危险区域内。

因此，将施工人员越界违章行为检测转化为判断施工人员在xOy平面上的投影是否落在危险区域内。对于上述判定问题，采用Franklin提出的PNPoly算法[20]，其基本原理为：从一个目标点引出一条射线，统计这条射线与多边形的交点个数。若有奇数个交点，则说明目标点在多边形内，若为偶数个交点，则在外。其具体实现过程如下：

假设圈定的多边形由n个传感器节点组成，第i个传感器节点的坐标为(xi,yi,0)，其中1≤i≤n，施工人员的三维坐标为P(a,b,c)。现作一条沿x轴正方向的射线y=b(x>a)，可计算出其与相邻两节点(xi,yi,0)和(xj,yj,0)形成线段的交点的横坐标：

(1)

若xcross>a且min(xi,xj)≤xcross≤max(xi,xj)，则说明该射线与多边形的一条线段存在交点。同理可计算出该条射线与多边形其余线段不同交点的个数。若交点个数总和为奇数，则施工人员位于安全区域内；若为偶数，则施工人员位于施工危险区域。

图2展示了该算法在变电站场景中的应用。从上图可以看出，施工人员①所引出的射线与划定的安全区域有奇数个交点，从而判定该施工人员处于安全施工区域；施工人员②的垂直高度小于最大高度H，且其在xOy平面的投影点所引出的射线与安全区域有奇数个交点，因而施工人员②也位于安全区域；而施工人员③引出的射线与安全区域的交点个数为偶数，从而判定该施工人员未处于安全施工区域，存在越界违章行为。

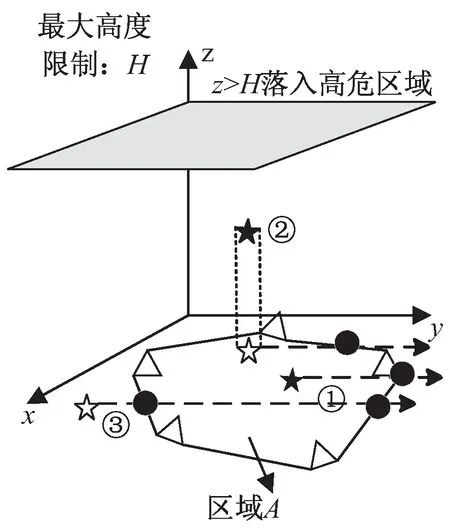
图2 PNpoly算法在变电站场景应用示意图

3 基于混合指数幂分布的噪声容错超宽带定位(MoEP-NULoC)算法

3.1 问题建模

从第2节容易得知，所提出的UWB-VEF方案其越界违章行为检测性能取决于UWB节点的定位精度,然而如前所述，UWB技术是一种基于测距的无线定位技术，其定位精度依赖于节点间距离信息的完备和准确程度。在变电站改扩建场景中，持续的电磁干扰和容积率偏高的复杂施工环境将不可避免地导致结点间距离信息的缺失和失真。为此，有必要设计一个鲁棒的UWB定位算法，其目的是基于缺失和失真的距离信息以及锚节点的位置准确定位出施工人员的所在位置。

假设有n个无线传感器节点Xi={xi1,xi2,xi3}∈R3部署在变电站中，节点间的真实距离信息可表示为D∈Rn×n，其中距离矩阵D中的元素定义如下：

dij=‖Xi-Xj‖2，i,j∈{1,2,…,n}

(2)

同时，将实际采样到的距离信息记为采样矩阵M，由于M是缺失和失真的，因此有：

PΩ(M)=PΩ(D+N)

(3)

其中，N为噪声矩阵，PΩ(·)为正交投影算子，其定义为：

(4)

其中，Ω表示采样矩阵M中非缺失元素的下标集合。

目的是基于缺失和失真的采样矩阵M重建真实距离矩阵D，其难点在于如何建模未知噪声N。不同于已有的无线定位噪声建模技术，这里引入混合指数幂分布(MoEP)来拟合复杂环境下的未知噪声，其动机在于已有研究表明MoEP具有超强的分布拟合能力[21]，理论上能逼近几乎任意的连续分布。此外，为了补全缺失的节点间距离信息，通过利用欧氏距离矩阵天然的内在低秩性，引入低秩矩阵分解技术来建模矩阵低秩属性。为此，提出的基于混合指数幂分布的距离矩阵补全模型(mixture of exponential power distribution based distance matrix completion，MoEP-DMC)可以建模为：

(5)

其中，ui和vj分别表示矩阵U的第i行和矩阵V的第j行，nij为测距过程中引入的未知噪声，根据前面的讨论，假设噪声nij服从混合指数幂分布，即：

(6)

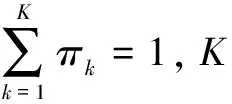
(7)

其中，η为精度参数，p为形状参数，Γ(·)为gamma函数。

3.2 MoEP-DMC模型求解

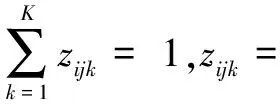
(8)

(9)

为了便于表示，引入变量Z=(zij)n×n，N=(nij)n×n，Θ={π,η,U,V}。由此可以写出完全似然函数：

(10)

通常为了求解方便，往往将式(10)转化为完全对数似然函数：

l(Θ)=logP(N,Z;Θ)=

(11)

确定噪声分量数K在模型中非常重要，因此采用了Huang等人[22]提出的有效方法来选取混合指数幂噪声的数量，为此构建了下列MoEP模型：

(12)

其中，

(13)

其中，ε是一个很小的正数(ε=10-6)，λ是一个可调参数(λ>0)，Dk表示第k个噪声分量中的自由参数数量。

由于目标函数(12)式中含有隐变量zijk，因此无法直接最大化该式来求解。因此引入EM算法[23]来求解该模型。

假设Θ(t)={π(t),η(t),U(t),V(t)}是在第t次迭代时的参数估计。在E步中，基于贝叶斯定理，可以计算出在给定nij的情况下zijk的数学期望：

(14)

基于上述数学期望，可以构造出目标函数Q函数：

(15)

在M步中，通过最大化Q函数，可以更新参数Θ。这里使用交替更新参数的方法来更新参数Θ中的各个分量。

更新参数π：

(16)

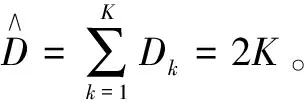
更新参数η：

(17)

更新参数U,V：

为了更新参数U,V，可以最大化Q函数中有关U,V的相关项，即最大化下列式子：

(18)

其中，W(k)∈Rn×n，其元素w(k)ij的定义如下：

(19)

为了求解式(18)，采用增广拉格朗日乘子法。让L=UVT，因此式(18)等价于：

(20)

然后增广拉格朗日函数可以写为：

(21)

其中，Λ∈Rn×n是拉格朗日乘数，ρ>0是惩罚参数。

现在需要优化U,V,L,Λ,ρ。在第m+1次迭代中，优化过程如下所示：

(22)

其中，α是一个正值。由式(22)可以看出，第一个子问题是后两个子问题的基础，因此只需对式(22)中的第一个子问题进行优化求解。这里采用交替优化方法，如下所示：

(1)更新U,V。

(23)

上式可以用奇异值分解方法进行求解。

(2)更新L。

对于i,j∈Ω，需要优化以下子问题来更新L：

(24)

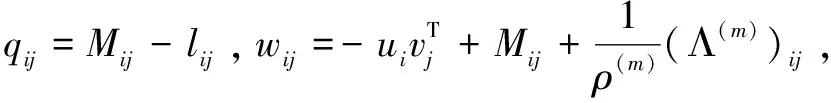
式(24)可以写成：

(25)

为了求解式(25)，针对qij求一阶导数，然后采用牛顿法找到其零点即可。

3.3 基于完整距离矩阵的节点定位

基于上述补全的欧氏距离矩阵，可以采用节点定位算法来求解所有未知节点的坐标。四点定位算法的基本思想是当未知节点到4个锚节点的距离已知时，便可利用四球交于一点的几何特性计算出自身的坐标。不妨设未知节点O距锚节点A、B、C、D的距离分别为d1,d2,d3,d4，锚节点A、B、C、D的坐标分别为(x1,y1,z1)，(x2,y2,z2)，(x3,y3,z3)，(x4,y4,z4)，可以写出以下方程组：

(26)

将式(26)中前三个式子依次减去第四个式子，经过整理可得如下式子：

AX=b

(27)

其中，

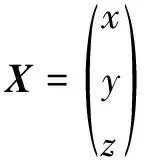
(28)

由此可得：

X=(ATA)-1ATb

(29)

通过上式即可计算出未知节点的坐标。

4 实 验

为了测试所提出的MoEP-NULoC算法的有效性，进行了一系列仿真实验。仿真实验场景设定为：在10 m×10 m×10 m的区域中随机布设40个节点，其中4个为锚节点，其余36个为未知节点。假设X∈R3×40和D∈R40×40分别表示节点的坐标矩阵和节点间的距离矩阵。首先对距离矩阵D添加噪声干扰得到含噪矩阵Dnoise，接着从Dnoise中随机采样部分元素作为已知的采样距离数据，然后利用所提出的定位算法对距离矩阵进行补全并计算所有未知节点的坐标。为了验证算法的优劣，使用距离矩阵的重构误差和坐标矩阵的定位误差来衡量所提出算法的有效性，两者定义分别如下：

(1)重构误差：

er=‖Dr-D‖F/‖D‖F

(30)

其中，Dr表示重构后的欧氏距离矩阵。

(2)定位误差：

el=‖Xl-X‖F/n

(31)

其中，Xl表示由所提出算法获得的节点坐标矩阵。

为考察算法在不同采样率/不同噪声污染情形下的性能，设计了3组不同的实验，实验1～3分别表示无噪声实验、高斯噪声实验以及混合噪声实验。在这3组实验中，将所提出的MoEP-NULoC算法(下面简称MoEP)与文献[16]所提出的奇异值阈值算法SVT以及文献[18]所提出的循环加权中值算法CWM做了对比。

实验1：无噪声实验。

在无噪声的情况下，欧氏距离矩阵D中除了一些元素缺失外，其余测距信息都是准确的。图3(a)和图3(b)展示了对距离矩阵进行不同比例采样情况下的距离矩阵重构误差及传感器节点定位误差的变化情况。

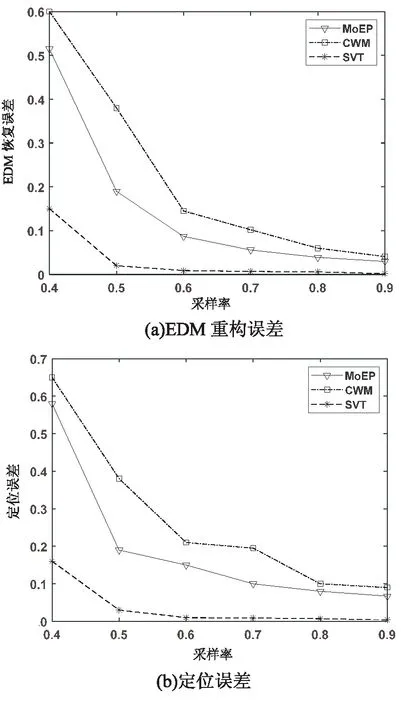
图3 无噪声情况下的误差变化

由图3可以看出，在无噪声情况下，SVT算法的性能要优于MoEP与CWM，MoEP与CWM的性能基本相同。这是由于距离矩阵中不含有噪声，因此仅仅是矩阵补全的SVT算法表现良好，而MoEP与CWM将采样欧氏距离矩阵视为含噪的矩阵，固在性能方面劣于SVT算法。

实验2：高斯噪声实验。

为验证两种算法在高斯噪声环境下的性能，将均值为0、方差为1的高斯噪声添加到样本距离矩阵中，模拟出采样信息中包含高斯噪声的情形。实验结果如图4所示。

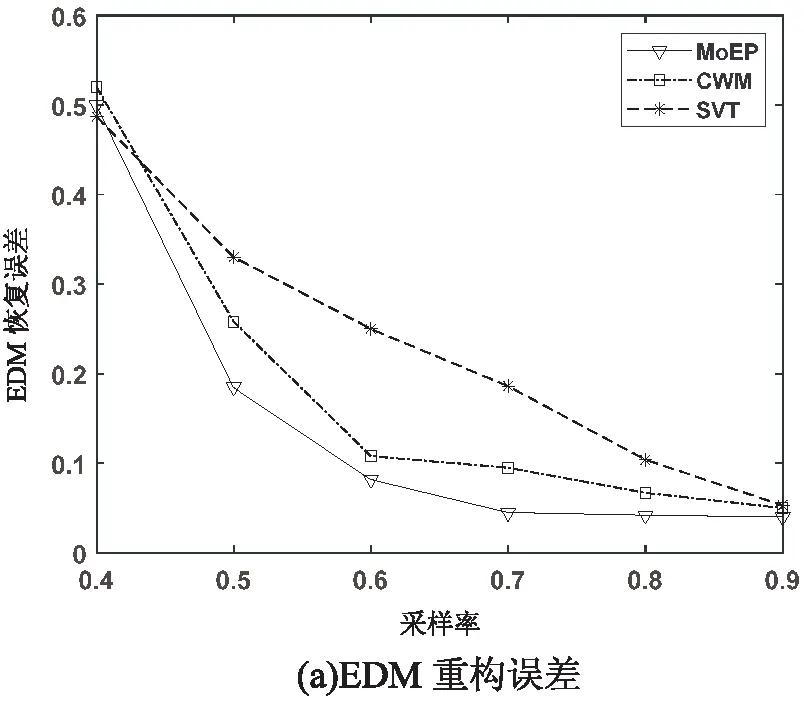
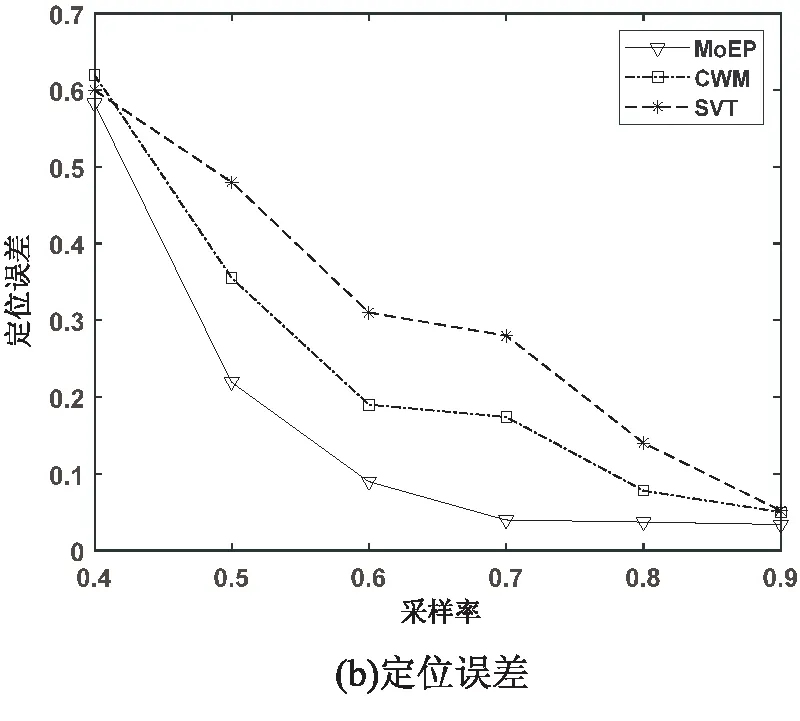
图4 高斯噪声情况下的误差变化

从实验结果可以看出，在不同的采样比例下，MoEP的性能均要优于CWM与SVT，这是因为高斯噪声是指数幂噪声的一种特殊情况[22]，固MoEP能较好地拟合高斯噪声。从图中可以看出，在采样比例为60%的情况下，MoEP算法的EDM重构误差和节点定位误差已降至0.1以下，具有较高的定位精度。

实验3：混合噪声实验。

在实际定位中，噪声往往是不可预知的复杂噪声。因此为了模拟实际定位中的复杂噪声，将复杂噪声设置为以下分量的混合：(1)在[-1,1]上服从均匀分布的噪声；(2)均值为0，方差为1的高斯噪声；(3)均值为0，方差为0.2pp(p=0.5)的指数幂噪声。图5展示了在不同采样率下EDM重构误差和定位误差的变化情况。

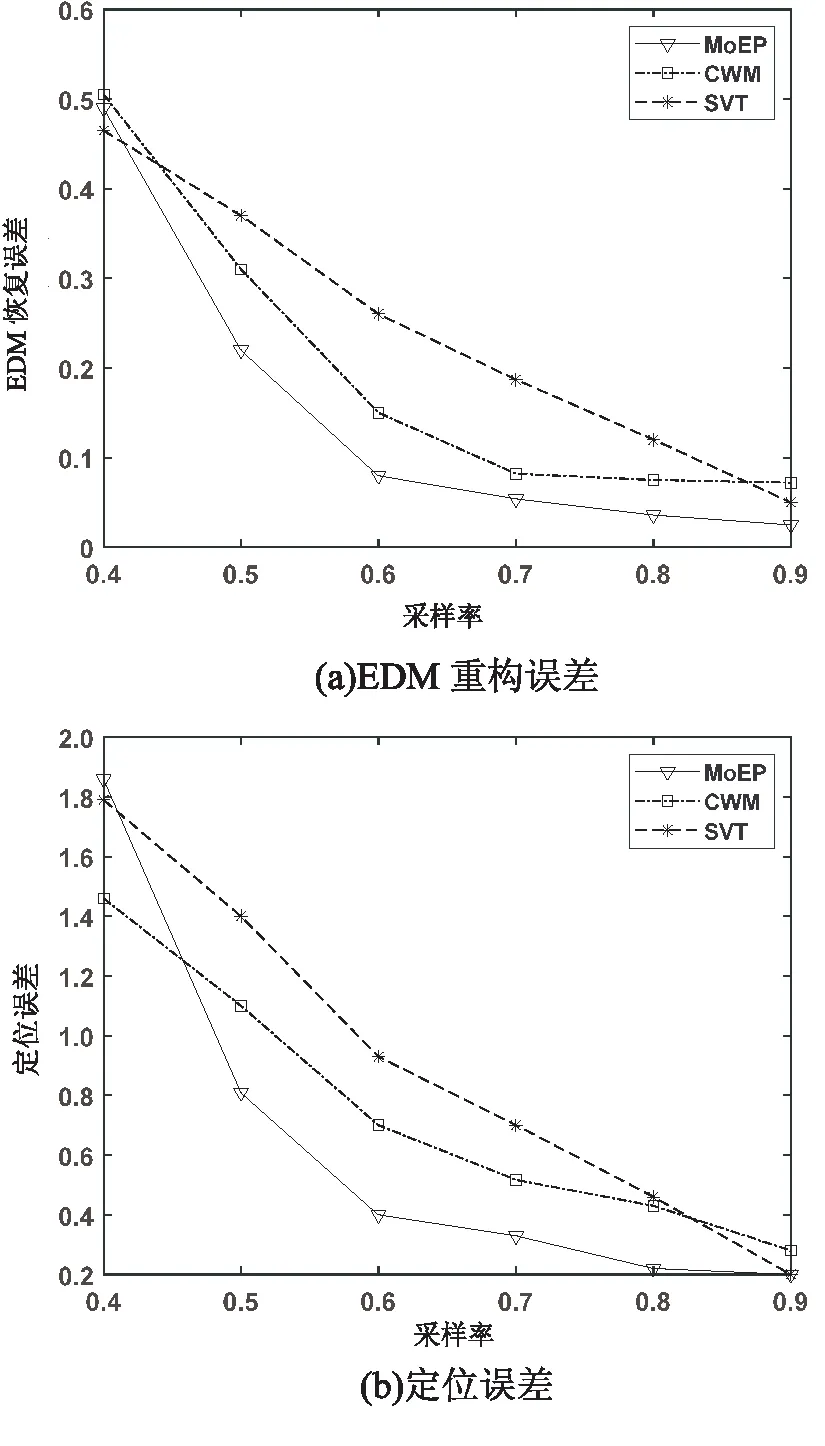
图5 混合噪声情况下的误差变化

从图5可以看出，在混合噪声情况下，当采样率大于等于0.5时，MoEP算法的EDM重构精度和定位精度都要优于CWM算法和SVT算法，这说明MoEP能够更好地拟合实际定位过程中的混合噪声。

从以上三个实验的实验结果可以看出，在无噪声的情况下，SVT算法的性能要优于MoEP算法和CWM算法，MoEP与CWM则表现相当；而在高斯噪声和混合噪声的情况下，MoEP的表现要优于CWM和SVT。正如前文所说，实际定位中的噪声往往是不可预知的复杂噪声，因此可以得出结论：与CWM以及SVT相比，MoEP能够更好地拟合实际中的噪声，可以更准确地定位变电站中的施工人员。

5 结束语

该文旨在面向变电站改扩建工程设计一种基于UWB定位的高程越界违章行为检测算法。然而，在实际的变电站改扩建场景中，持续的电磁干扰和容积率偏高的复杂施工环境往往导致UWB节点间距离信息缺失和失真，这使得传统的基于测距的定位算法变得不可用。为此，针对这一关键问题提出一种基于混合指数幂分布的噪声容错UWB定位算法。该算法一方面利用了混合指数幂分布对任意连续分布数据的渐近拟合属性，另一方面利用了欧氏距离矩阵的先验低秩属性，通过融合机器学习领域流行的低秩矩阵补全技术和简单易行的四点定位算法，估算出所有未知节点的三维空间坐标。仿真实验结果表明，与已有的其他算法相比，基于混合指数幂分布的噪声容错UWB定位算法在复杂噪声环境下可以实现更精确的定位。同时，所设计的基于噪声容错UWB定位的高程越界检测方案具有广泛的工程应用前景，不仅适用于该文所述的变电站改扩建场景，也适用于各种复杂环境下的基建施工场景。