基于Q-学习的底盘测功机自适应PID控制模型
2022-05-30郭兰英王润民
乔 通,周 洲,程 鑫,郭兰英,王润民
(1.长安大学 信息工程学院,陕西 西安 710064;2.陕西省车联网与智能汽车测试技术工程研究中心,陕西 西安 710064)
0 引 言
汽车底盘测功机(转鼓试验台)主要包含滚筒和加载装置,以电涡流机输出加载力来模拟汽车在道路上行驶的场景,能够在室内对汽车进行综合测试,且对测试所需要的环境要求较低[1]。目前底盘测功机中大都采用标定PID参数或模糊PID控制法对加载的力进行控制,PID参数一经整定就不能改变。但电涡流机具有非线性、紧耦合的特点,所以上述两种策略的控制效果并不理想[2]。
随着机器学习的发展,强化学习已被广泛应用于PID在线调整等序列决策问题,取得了一定的效果[3-6]。在国内方面的相关研究中,张训等[7]采用积分分离PID算法,实现转速、励磁电流和转矩、励磁电流的两个双闭环控制器,满足了测功机的控制要求,但达不到现如今底盘测功机控制的工业要求;郭磊等[8]设计的模糊自适应PID算法有效提高了跟踪性能和调节速度,完成了对PID增益值的调整,此方法需要增益值从零开始调整,所需要的控制时间也相对较长;游博洋等[9]设计了基于神经网络PID控制器的外骨骼系统,有效的提高了外骨骼机器人的易用性和实用性;贾燕燕等[10]基于神经网络设计的自适应网络功率机制动态调整发射功率的大小,较好地解决了无线体域网中的传感器控制节能问题;赵明皓等[11]基于深度强化学习设计的无人艇自主航行控制算法,比传统的PID控制在稳定性以及抗干扰上具有优势。国外方面,V N Thanh等[12]使用Q学习算法设计的自适应PID控制器对伺服机器人进行控制,并验证了其优越性;P Kofinas[13]为了处理连续的状态-动作空间,设计了模糊Q学习代替传统的Q学习算法,仿真表明了其有效性。上述研究都取得了许多积极的成果,对该文研究的开展具有较好的借鉴意义。
该文分析了底盘测功机的加载方式以及常见强化学习算法的特点,结合其规律进行分析,并研发对应的状态空间、动作空间和奖励等等,训练Q表完成对PID增益值的自动调节。主要研究基于强化学习的PID策略设计出来的QPID控制器,对底盘测功机输出扭矩的控制效果。
1 强化学习控制策略设计
1.1 强化学习
强化学习是通过与外部的环境进行交互,每次交互会获得奖赏,再通过该奖赏指导下一次的行为,其目标是使智能体能够取得最大累积奖赏[14]。强化学习的结果是寻找出一个策略π:S→A,能够让每个状态s的值函数Vπ(s)或者状态-动作值函数Qπ(s,a)达到最大。Vπ(s)与Qπ(s,a)分别表示某个“状态”上或者是某个“状态-动作”上的累积奖赏[15]。
强化学习也在不断的发展,Q-Learning算法被认为是其中最主要的进展之一。Q-学习算法考虑了状态作用值函数Q,不考虑被控制系统确切的数学模型,通过时间差分对系统进行控制[16]。Q-Learning是RL中value-based的算法,其中的Q意为在某个时刻的状态时,选择某个动作可以获得相应的收益,环境状态会依据此次智能体的动作,反馈出其所获得的立即奖赏r,再依据r进行Q表的更新,公式如下:
Q(s,a)←Q(s,a)+α[r+γQ(s',π(s'))-
Q(s,a)]
(1)
其中,α为学习率,0≤α≤1。
算法1:Q学习算法。
Step1:初始化任意Q(s,a),∀a∈A,∀s∈S;
Step2: 循环每个episode;
重复
Step3:更新状态St;
重复
Step4:执行动作At,观察St+1和Rt+1
Step5:根据式(1)更新Q值;
Step6:St←St+1;
Step7:直到St达到最终状态ST;
Step8:直到episode结束。
1.2 底盘测功机自适应PID控制器设计
该文提出了一种基于Q学习算法的PID控制器,用于调整底盘测功机的扭矩输出,整个控制器的结构如图1所示。系统的直接控制由一个传统的PID完成,而参数的自适应调整是基于Q-学习算法在训练过程中获得的Q表,传统的PID实现输入电压的调节。控制器的输入为人为设定的加载力的目标值Fref,将每次调整之后的扭力值Fn(t)与目标值的误差量输入到PID中,进而完成此次的调整。待调节完之后,获得此次调节的扭力值Fn(t),把这次的扭力值进行离散化, 即可得到此次的状态n(t)。之后开始本次的Q表更新,总共有3个Q表,对应于PID的三个参数,一个参数对应到一张Q表上。当Q学习算法更新完毕之后,Q表最终会趋于稳定。此时在三张Q表中,选择某一个状态之后,每张Q表都会选择出此时PID控制器最优的增益值去调整。
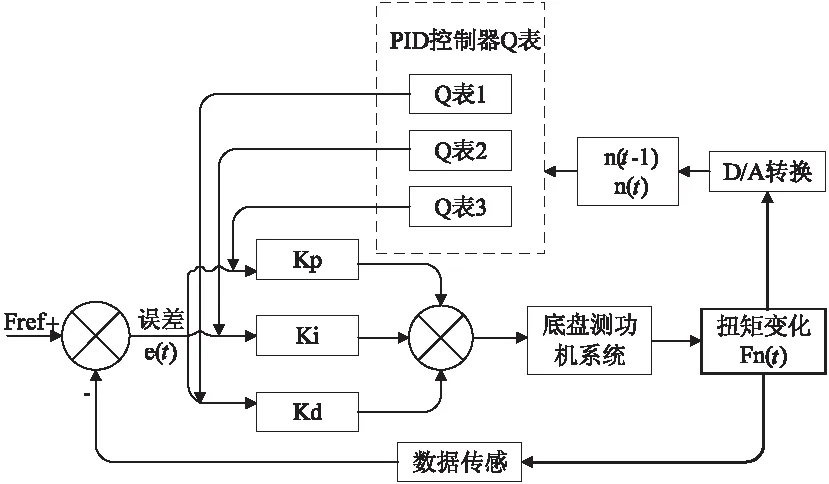
图1 基于QPID的底盘测功机系统控制器结构
2 结合Q学习的PID控制算法
对于Q学习最重要的一个问题,就是如何训练Q表。该文设计的控制器,需要通过三张Q表使得底盘测功机不同扭矩输出的状态,对应到PID策略的各个参数上。将Q学习策略与传统的PID策略进行结合,具体的训练过程如算法2所示。为了使得Q表可以快速收敛趋于稳定,实现了一种自适应学习率的算法——Delta-Bar-Delta[17]。在训练过程中,取得某个状态时的最佳参数之后,就根据公式计算出此次需要调整的输出量,输出量会通过PID控制器作用于底盘测功机,此时扭矩输出改变,进入到下一个状态。通过比较前后两个时刻的扭矩输出,就可以得到此次调整之后的立即奖赏Rp,使用Rp更新Q表,开始下一次的训练,如此循环。当Q表趋于稳定之后,Q表就含有了在每个状态下最优的PID参数,使用该参数即可控制底盘测功机的扭矩输出。
算法2:结合Q学习的PID控制算法。
Step1:初始化任意Qi(s,a)=0,∀a∈A,∀s∈S,i=1,2,3;
Step2:初始化学习率∂;
Step3:初始化ε-greedy策略的ε;
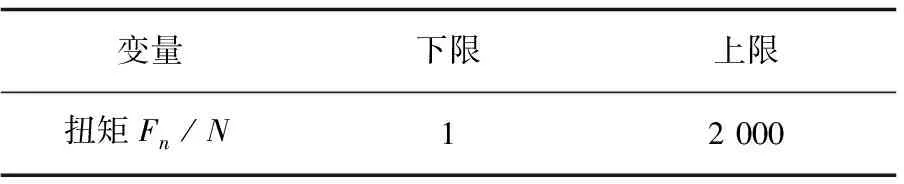
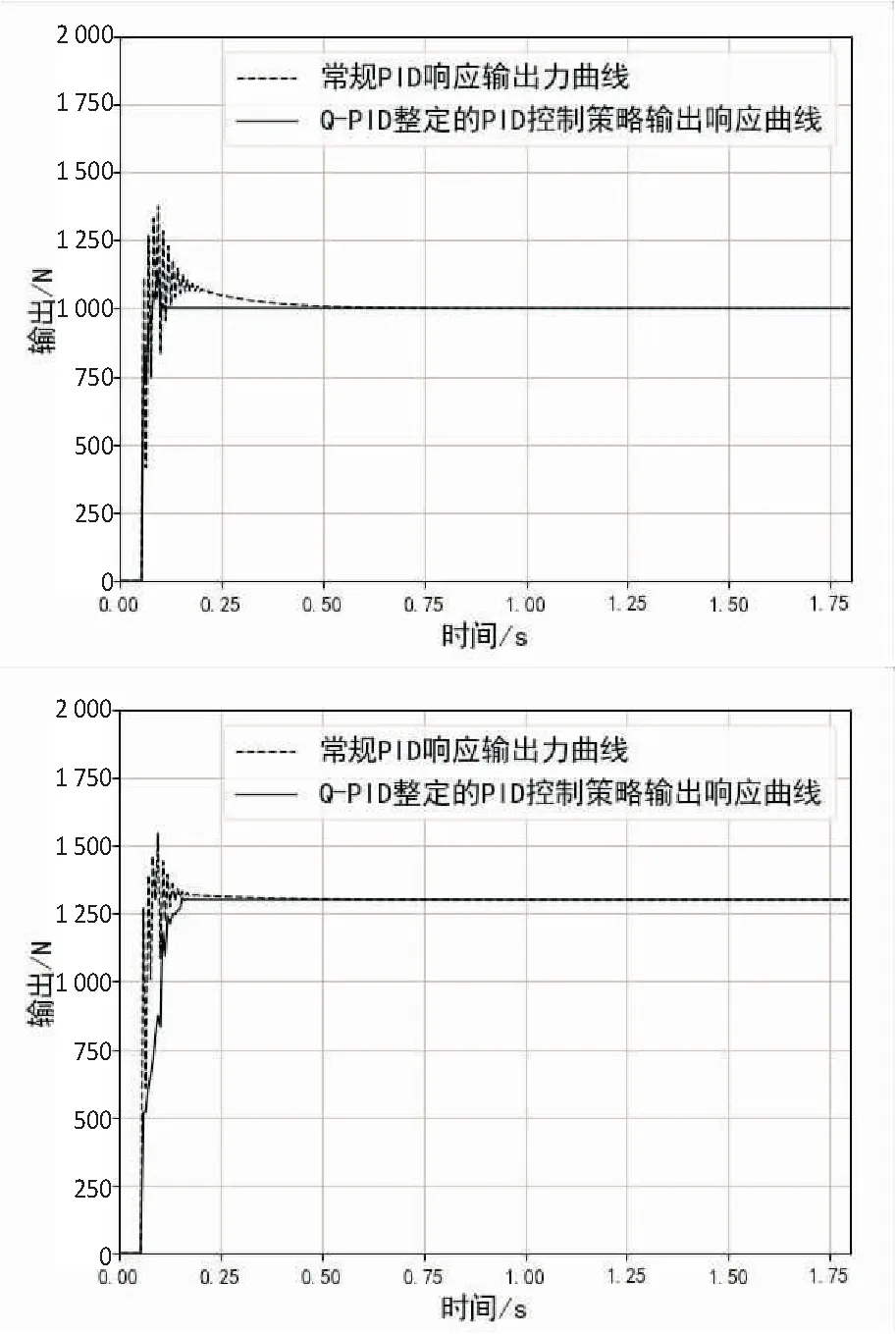
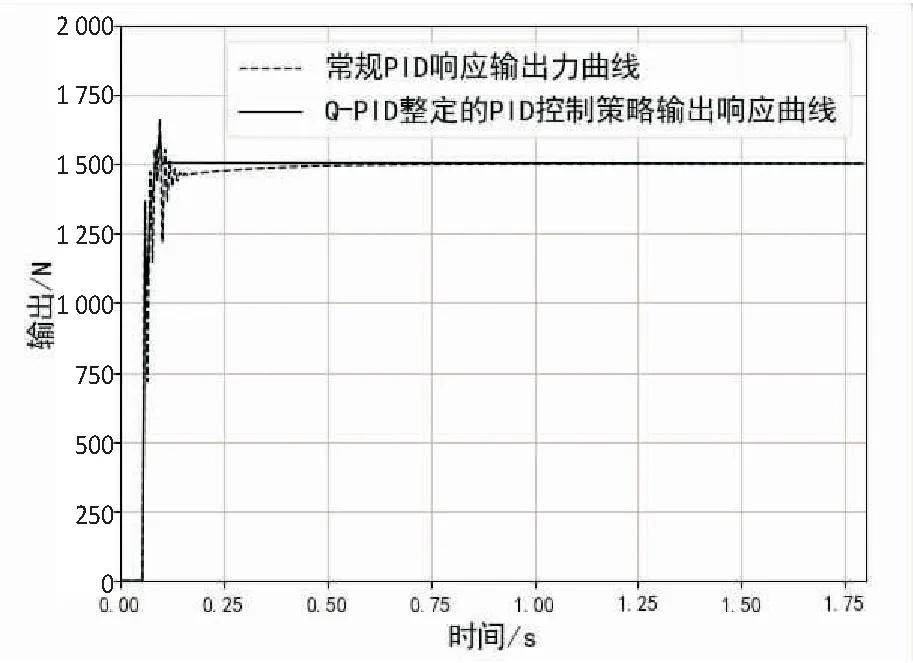
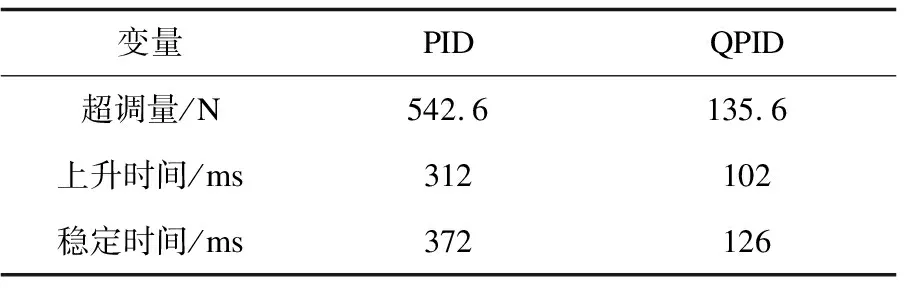
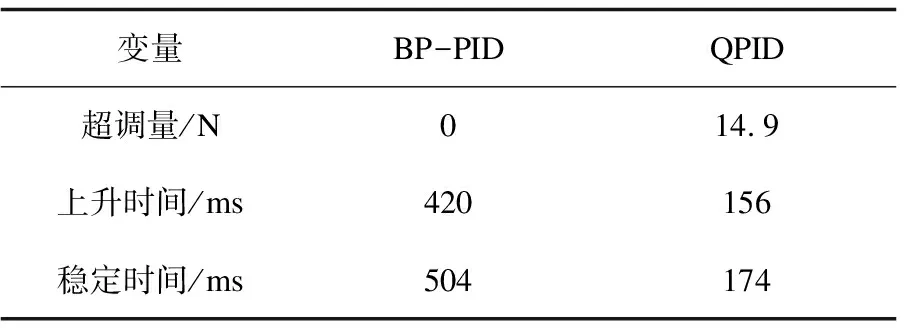
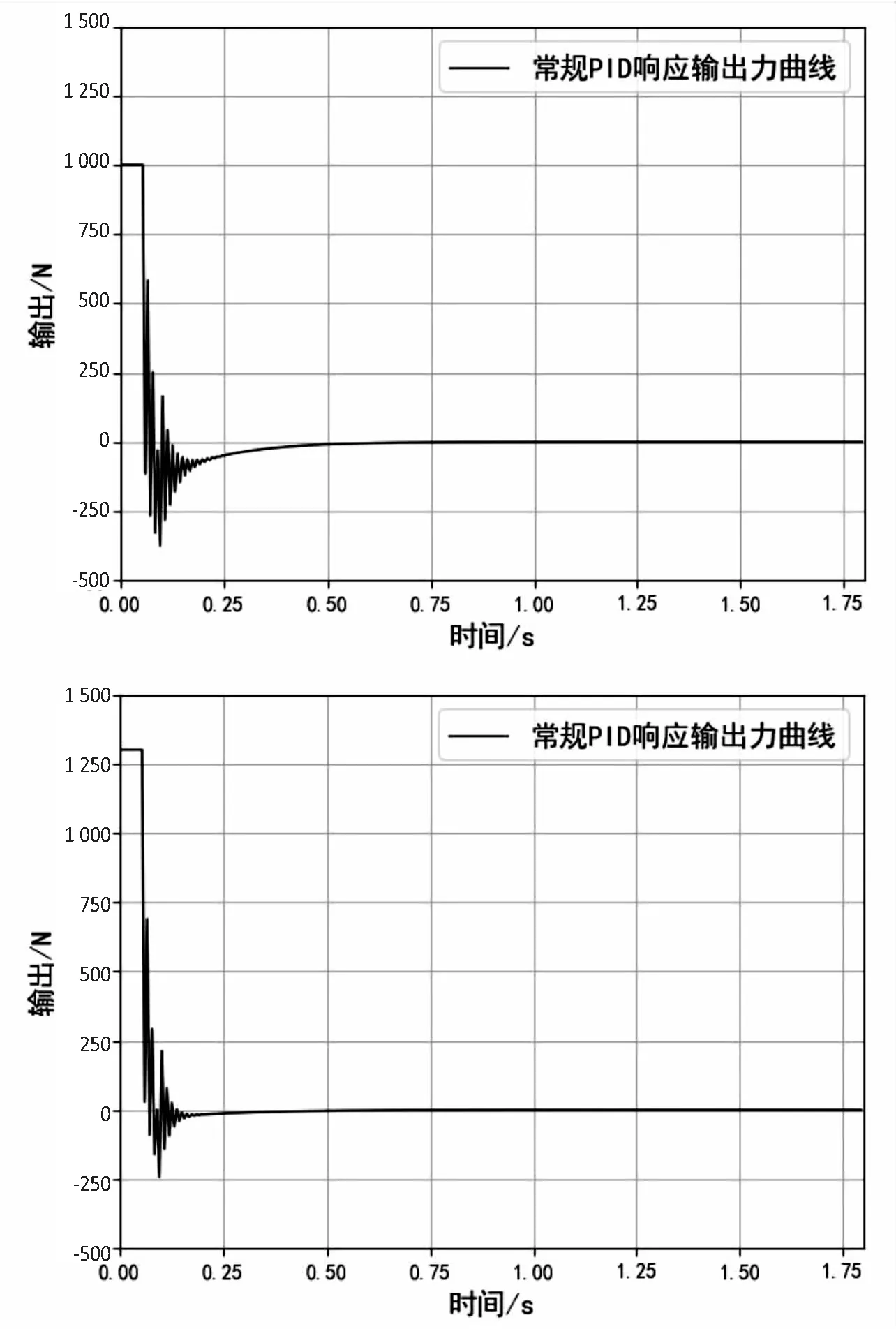
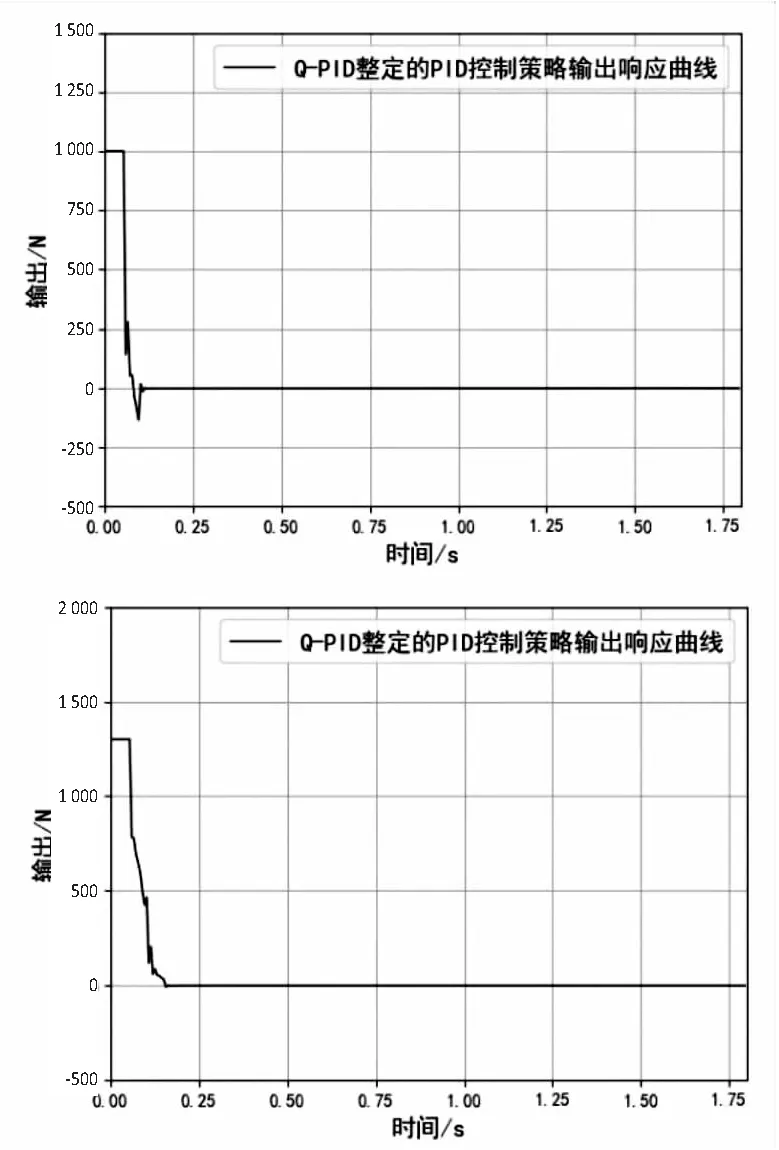
Step4:当episode Step5:t=0; Step6:初始化St(x(t),x'(t)); Step7:ε衰变(当episode>0.6×maxepisode,ε=0); Step8:fort=1;≤maxtime;t++ Step9:将状态St-1,St离散化,获得:n1(t-1)和n1(t); Step10:fori=1;i≤3;i++ Step11:遵循ε-greedy策略,根据n1(t-1)和n1(t)选择动作Ai; end Step12:根据PID输出,获得完整的输出; Step13:观察新状态St+1(x(t),x'(t)); Step14:获得的奖励Rp; Step15:将状态St+1离散化,获得:n1(t+1); Step16:更新Q1(s,a),Q2(s,a)和Q3(s,a)的学习率∂; Step17:用Rp和∂更新Q1(s,a),Q2(s,a)和Q3(s,a); Step18:St←St+1; end end 为了使得Q表尽快达到稳定,使用了一种自适应学习率的算法,其定义为: (2) 式中,Δαt是t增量;k是提高学习率的正常数值;Φ是折扣因子的正常数值;δt是时间步长t中的时间差(TD)误差,δt=Rt+1+γmaxQ(St+1,a)-Q(St,a);δt=(1-Φ)δt+Φδt-1。 通过使用上面的方法,将当前的TD误差与前面步骤中的累计TD误差进行比较,从而更新学习速率。当学习率较大时,改变符号,从而使其在下一次调整时调低。如果学习率太小,学习率会按照之前的变化趋势不断增加,使得收敛速度加快,所以时间步骤t+1中的学习速率为αt+1=αt+Δαt。三个Q表都将采用该算法,但对于每张Q表的参数设置会有不同。 由于加载力的状态值连续,且过于繁多,所以对于加载效果一样的情形,可选择同一组PID参数进行控制,因此可以把连续的加载力变量分成几个区间,同一个区间内的加载力值作为一个相同的状态。区间的设置使用与定义使用相同的规则,其定义为: (3) 其中,[x]=max{n∈Z|n≤x};n表示离散变量;xcon表示连续变量;xmin和xmax分别是xcon的下限和上限;N表示加载力被分成的区间数,文中N=20。N取决于模拟性能。扭矩Fn通过公式(3)区间划分,离散化设置的值如表1。 表1 设定离散化值 当给定当前状态之后,三个Q表都将根据ε-greedy方法选择每次的动作,此方法的定义如下: (4) 其中,ζ∈[0,1]是一个正态分布的随机数。 为了加快收敛的速度,ε的值会随着训练次数的增大而减小,在迭代次数达到某个数值后设为零,而具体的次数会根据训练表现来决定。在ε-greedy策略中,ε的值比较大,表示选取一个随机动作的概率也比较大。具体ε定义为: ε(eps)= (5) 其中,eps表示当前的episode,maxep是episode的最大值。 该文根据测功机系统的情况将立即奖赏分为三种情况:调节后加载力趋于设定力值,加载力远离设定力值和调节之后加载力无变化。 调控后扭矩趋于设定值。根据at收到的参数进行调节,所获得的扭矩Fn(t)与目标值Fref的相差结果,若是远小于t-1扭矩Fn(t-1)与Fref的相差结果,意为此次的调控有效,设定此次调整的奖赏为相邻两次扭矩输出的差值。 调控后扭矩远离设定值。根据at得到的参数进行调节,所获得的扭矩Fn(t)与设定值Fref的相差结果,若是远大于t-1扭矩Fn(t-1)与Fref的相差结果,意为此次的调节为错误调节,奖赏为负值。 调控后扭矩无变化。根据at得到的参数进行调节,所获得的扭矩Fn(t)与设定值Fref的相差结果,若是与t-1扭矩Fn(t-1)与Fref的相差结果,二者相差不超过20 N,意为此次的调节无效果,即奖赏值为0。综上,奖励计划如下: (6) PyCharm是一款系统模型库的功能十分丰富的仿真平台,该文使用PyCharm建立仿真系统,使用模拟的数据进行实验,验证使用QPID策略的可行性。选择相同的初始条件针对底盘测功机的恒力运行状态进行仿真控制,分别使用传统PID策略、BP-PID策略以及文中提出的QPID策略进行系统仿真,根据结果进行对比分析。 (1)QPID控制策略与传统PID控制策略的对比。 图2为分别使用两种控制策略,输出力从0 N分别到1 000 N、1 300 N和1 500 N的加载力响应曲线。 在仿真中,对比传统的PID控制策略,基于QPID控制策略加载力响应曲线的波动较小,一般在120 ms左右就可以实现加载力的响应过程,146 ms后趋于稳定。传统PID策略下扭矩输出响应曲线的波动较大,一般在249 ms左右实现扭矩输出的响应,在358 ms后才达到设定值。基于QPID策略下的调整周期相较于传统的PID策略缩短至40%。 图2 QPID控制器与PID控制器的输出力响应曲线 加载至1 000 N的响应曲线特征如表2所示。 表2 QPID控制器与PID控制器响应曲线特性 在加载力目标值为1 000 N时,与QPID控制器(135.6 N)相关的曲线的超调远低于传统PID控制器(542.6 N)。除此之外,QPID控制器(126 ms)的稳定时间比PID控制器(372 ms)的稳定时间短。 (2)QPID控制策略与BP-PID控制策略的对比。 图3为分别使用QPID与BP-PID控制策略,输出力从0 N分别到1 000 N、1 300 N和1 500 N的加载力响应曲线。 在仿真中,基于QPID的策略比BP-PID策略更快达到稳定,在120 ms左右就可以实现加载力的响应过程,在146 ms后趋于稳定。而BP-PID策略下扭矩输出的曲线上升时间与稳定时间较慢,在425 ms左右实现扭矩输出的响应,在524 ms后达到设定值。基于QPID控制策略下的调整周期相较于BP控制策略的调整周期缩短至27.9%。 图3 QPID控制器与BP-PID控制器的 输出力响应曲线 加载至1 300 N的响应曲线特征如表3所示。 表3 QPID控制器与PID控制器响应曲线特性 在加载力目标值为1 300 N时,与QPID控制器(14.9 N)相关曲线的超调大于BP-PID控制器(0 N)。另外,QPID控制器(156 ms)的稳定时间比BP-PID控制器(504 ms)短。 根据国家质量监督检验检疫总局2018年发布的底盘测功机使用标准,底盘测功机运行状态的工业要求误差不大于2.0%,加载响应需要在300 ms以内达到目标值的90%。以上三种控制策略下的扭矩输出的误差曲线如图4所示。 由图4可知,QPID控制的系统加载力响应曲线的最大振幅146 ms后小于10 N,达到工业要求;BP-PID控制器的扭矩输出曲线的最大振幅420 ms后高达50 N左右;传统PID控制策略下的扭矩输出曲线的最大振幅321 ms后约为27 N。基于QPID控制策略可以满足底盘测功机使用所需要达到的工业要求,其加载力的响应曲线正常,跟理论分析的结果保持一致。 (a)常规PID策略下的误差曲线 (b)QPID策略下的误差曲线 针对底盘测功机的加载控制问题,提出了一种基于Q学习的PID控制策略,使用QPID对三个增益值进行调整,使其能够快速稳定达到加载目标值,最后完成了与另外两种策略的比对试验。通过分析对比试验的结果,证明在底盘测功机上使用QPID控制器,可以让加载力的响应时间缩小到120 ms,在146 ms后稳定到工业要求的误差范围之内,控制周期缩短明显。说明基于Q学习的PID调节策略可以在底盘测功机上得到较好的应用。2.1 自适应学习率
2.2 离散化
2.3 ε-greedy策略
2.4 奖励策略
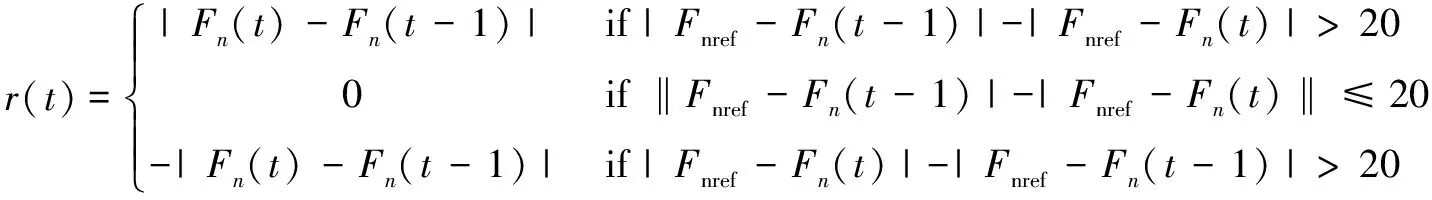
3 算法实验研究

4 结束语
