基于改进密度峰值聚类算法的图像分割
2022-05-30张力丹王军锋
张力丹,王军锋
(西安理工大学 理学院,陕西 西安 710054)
0 引 言
聚类作为一种无监督的分类方法,能够用于无标签的数据对象的划分[1]。作为数据处理的技术,聚类分析已经广泛应用于多个领域,例如计算机科学、数学、经济学等。聚类可分为划分聚类、层次聚类、基于密度的聚类和基于网格的聚类等。K-means作为最为经典且具代表性的划分聚类,需在给定簇类个数的前提下,经过反复迭代获取最优分组,但是该方法很难用于非球形聚类数据的无监督划分[2]。FCM聚类算法作为软聚类法的代表之一,需要构造各数据点归属于某一簇类的隶属度函数,而同一数据点可同时归属至不同的簇类中[3]。DBSCAN算法在限制Eps邻域及最小核心点MinPts下,通过建立了密度可达及直接密度可达一套机制将数据进行归类,但很难发现密度变化差异明显的簇类[4]。
2014年Alex Rodriguez发表于《Science》上的密度峰值聚类(DPC)算法[5],其核心思想在于对簇类中心的刻画。该算法认为簇类中心同时具有两个特点:一是具有较大的密度,即簇类中心被密度较小的数据点包围;二是与其他局部密度更高的点的距离较大。该文将对DPC算法中的敏感参数截断距离dc进行自适应选取,并将改进的DPC算法应用于图像分割。
1 密度峰值聚类算法
DPC算法在含n个数据点的数据集中定义了各点i(i=1,2,…,n)的局部密度ρi和局部距离δi。局部密度ρi的计算公式如下:
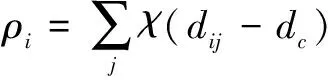
(1)
(2)
式中,dij为各数据点间的相似度;dc为截断距离,本质为簇类中心的邻域半径。上述公式表明,各数据点的局部密度为dc邻域内所含数据点个数[6]。截断距离dc的选取基于各数据点的相似度,取值为升序排列的第c个数据点间的相似度dij,c的计算公式为:
c=⎣N×P+0.5」
(3)
式中,N为数据点间相似度总数;P为截断距离dc的取值阈值。因此,截断距离dc仍需依赖人为选取的阈值P。各数据点的局部距离δi刻画了各数据点与密度更高点之间的距离,具体计算公式如下:
(4)
上式表明,对于局部密度最大的数据点,其局部距离为该点与其他数据点间相似度的最大值[7];其余数据点的局部距离则为该点与其他数据点间相似度的最小值。计算簇类中心的选择阈值γi:
γi=f(δi,ρi)
(5)
上式表明,阈值γi为关于局部密度ρi和局部距离δi的函数。文献[4]将前K个降序排列的γi所对应的数据点作为簇类中心。
2 自适应截断距离dc的DPC算法
DPC算法在计算局部密度ρi时采用基于ε近邻的方式,将数据点xi的dc邻域内包含的数据点个数作为该点局部密度。dc的选取依赖于人为确定的阈值P,P按经验取值为1%~2%。DPC算法核心在于计算各数据点的局部密度ρi和局部距离δi,并将局部密度ρi和局部距离δi的局部极值点作为局部峰值点,也就是簇类中心。其中局部距离δi的计算依赖于局部密度ρi,而局部密度ρi的计算又依赖于截断距离dc,因此dc的选取对密度峰值聚类结果的影响尤为重要[8-10]。
然而不同的数据内部稀疏程度不一致,若仅靠经验值选取截断距离dc势必导致错误归类。阈值P过大会导致截断距离dc取值过大,容易将本不属于同一簇类的像素点合并;阈值P过小又会导致截断距离dc取值过小,容易将本属于同一簇类的像素点分成多个簇类,因此基于阈值P的截断距离dc并不可靠且影响了局部密度ρi的全局可靠性[11]。
2.1 基于最小化信息熵的截断距离dc
DPC算法中定义的局部密度ρi依赖于截断距离dc以及数据点间的相似度dij。实际中,数据集在不同维度上的分量通常不在一个数量级上[12-13],为此该文重新定义数据点间的相似度dij。计算数据集X的第d维分量的极差Ad:
Ad=max(Id)-min(Id)
(6)
将数据点xi和xj间的相似度dij定义为:
(7)
式中,D为数据维数。计算当前数据点xi的dc邻域内相似度均值μdc_i:
(8)
式中,p和q为当前数据点xi的dc邻域内所含数据点;N_i为该点dc邻域内所含数据点的个数。设数据集含有n个数据点,引入高斯核将当前数据点的局部密度ρi定义为:
(9)
改进的局部密度增加了数据点xi的dc邻域内所含数据点的影响权值,使得同一簇类当中的数据点相似程度更紧密。各数据点的概率密度定义为:
(10)
对于一个包含n个随机变量x1,x2,…,xn的系统,其信息熵为:
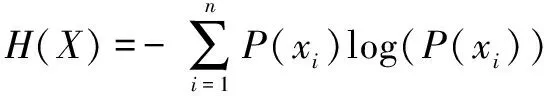
(11)
则基于公式(10)得到的数据集信息熵为:
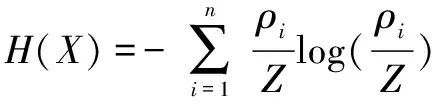
(12)
由上式可知,改进方法后的信息熵中唯一变量为截断距离dc。随机事件发生的概率越大提供的信息越少,信息熵体现出事件的不确定性。因此作为一种量化指标,信息熵越小对应的系统越稳定[14-15]。
该文将使得信息熵最小的dc值作为截断距离dc的最优取值,具体如下:
dc=arg minH(X)
(13)
2.2 基于改进DPC算法在图像分割上的应用
在DPC算法中,若局部密度ρi和局部距离δi越大,则对应的数据点xi越有可能成为簇类中心。DPC算法通过公式(5)将降序排列的前K个γi所对应的数据点作为簇类中心,这种选取方式本质上仍需人为选择。为了自适应地选择图像的簇类中心,定义簇类中心点选取的阈值γmin为:
γmin=E(ρ)×E(δ)
(14)
式中,E(ρ)和E(δ)分别为数据点的局部密度均值和局部距离均值。若当前数据点为簇类中心,则该数据点的局部密度ρi和局部距离δi应远大于其余数据点。将符合公式(14)的数据点作为初始的簇类中心。
计算各数据点的ρi和δi的乘积,并记作γi:
γi=ρi×δi
(15)
在确定阈值之后,对初始判断的簇类中心进行深度筛选,最终确定的簇类中心集合C为:
C={ci|γi>γmin,δi>dc,ci∈X}
(16)
上式表明,dc作为一个特殊的邻域半径,应当小于簇类中心之间的距离。因此,选择γi大于阈值γmin且δi大于dc的对应点作为簇类中心。
由于DPC算法需要计算数据点之间的距离,以此来判断数据点之间的相似程度,因此对于一般图像而言,将像素点作为输入数据进行密度峰值聚类会耗时很久。为解决DPC聚类在处理较大数据集用时较久这一问题,采用并行分块处理图像数据的方式。将一般图像划分成M×N个块,对每一块依次使用改进的密度峰值聚类进行分割,将每一块的像素点作为输入数据,得到每一块的聚类中心(共计k'个)。在此基础之上,使用提出的改进的密度峰值聚类,重新对M×N个块中的k'个聚类中心进行二次聚类,此次聚类的输入数据为k'个聚类中心,输出数据为最终的k个聚类中心。经过两次聚类之后得到最终需要的聚类中心,最后对所有数据按照相似度进行归类,得到最终的分割结果。基于改进DPC算法的图像分割流程如下所示。
算法1:基于改进算法的图像分割。
输入:图像I
将图像进行分块处理,共计M×N个块.
Whilei≤最大迭代次数M×N
Run 第一次调用改进的DPC算法:
提取像素点特征:X,Y,R,G,B,LBP(分别为位置特征X、Y,颜色特征R、G、B,LBP纹理特征);
利用公式(7)计算像素点间的相似度dij;
利用公式(13)计算截断距离dc;
使用公式(9)和公式(4)分别计算局部密度ρi、计算局部距离δi;使用公式(14)计算簇类中心选择阈值γmin;并使用公式(16)选取簇类中心;
遍历归类剩余像素点;
将属于同一类的像素点进行合并;
输出当前块的聚类结果;
End
End
二次调用改进的DPC算法,将第一次聚类中属于同一类的区域进行合并;
输出最终分割结果.
3 实验结果与分析
3.1 实验环境
对多个彩色数字图像数据集使用文中算法进行分割,并将文中算法与K-means、FCM、DPC算法和文献[5]中的算法进行对比,验证改进算法具有较高的分割精度,实验硬件为i5-6500 CPU @ 3.20 GHz,RAM 4.00 GB,64位操作系统,实验软件为Matlab R2016b。
3.2 图像分割评价指标
3.2.1 概率兰德指数(PRI)
设图像共包含N个像素点,Sg为GroundTruth,使用不同算法得到的分割结果记为Stest。当Sg的第i个像素与Stest中第j个像素具有相同标签时,将该事件记作Aij,该事件发生的概率为pij。PRI指标取值范围为[0,1],数值越大算法分割精度越高。PRI指标具体计算方式为:
(17)
3.2.2 变换信息量指数(VOI)
计算分割结果Stest和GroundTruth图像Sg信息熵之和,并减去二者的联合信息熵,将计算结果作为VOI指标值。该指数代表相对变化的信息量,VOI越小实验精度越高,且越接近GroundTruth。VOI指数具体计算方式为:
VOI(Sg,Stest)=H(Sg)+H(Stest)-2H(Sg,Stest)
(18)
3.2.3 欠分割误差(USE)
所谓的“欠分割”是指前景目标错误地划分到背景中,反之“过分割”提取到的前景中包含本属于背景中的某些区域。USE指标能够衡量图像中的分割精度,对于包含N个像素点的数字图像,其在不同算法下得到的分割结果Stest与Sg分别由nb和nbst个不相交的区域构成:
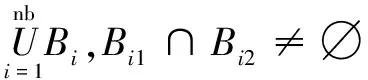
(19)
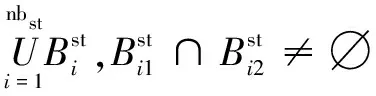
(20)
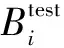
(21)
式中,B为分割结果图像与GroundTruth图像中包含共同像素点个数的最小值。据公式(21)可知,USE越小实验精度就越高。
3.3 结果分析
3.3.1 二维数据聚类效果
(1)二维数据集。
选用6个不同数据集进行实验分析,表1给出了数据集的样本数和真实类别数。图1为原始数据分布。
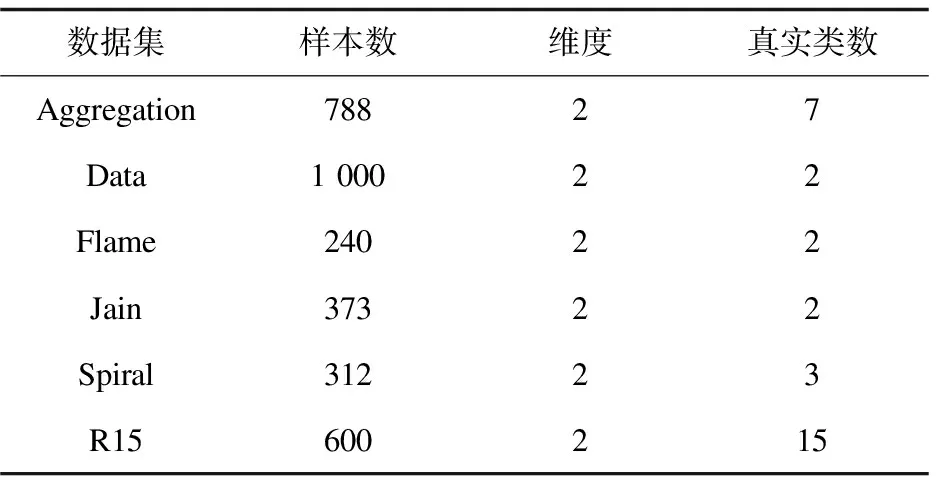
表1 不同数据集信息
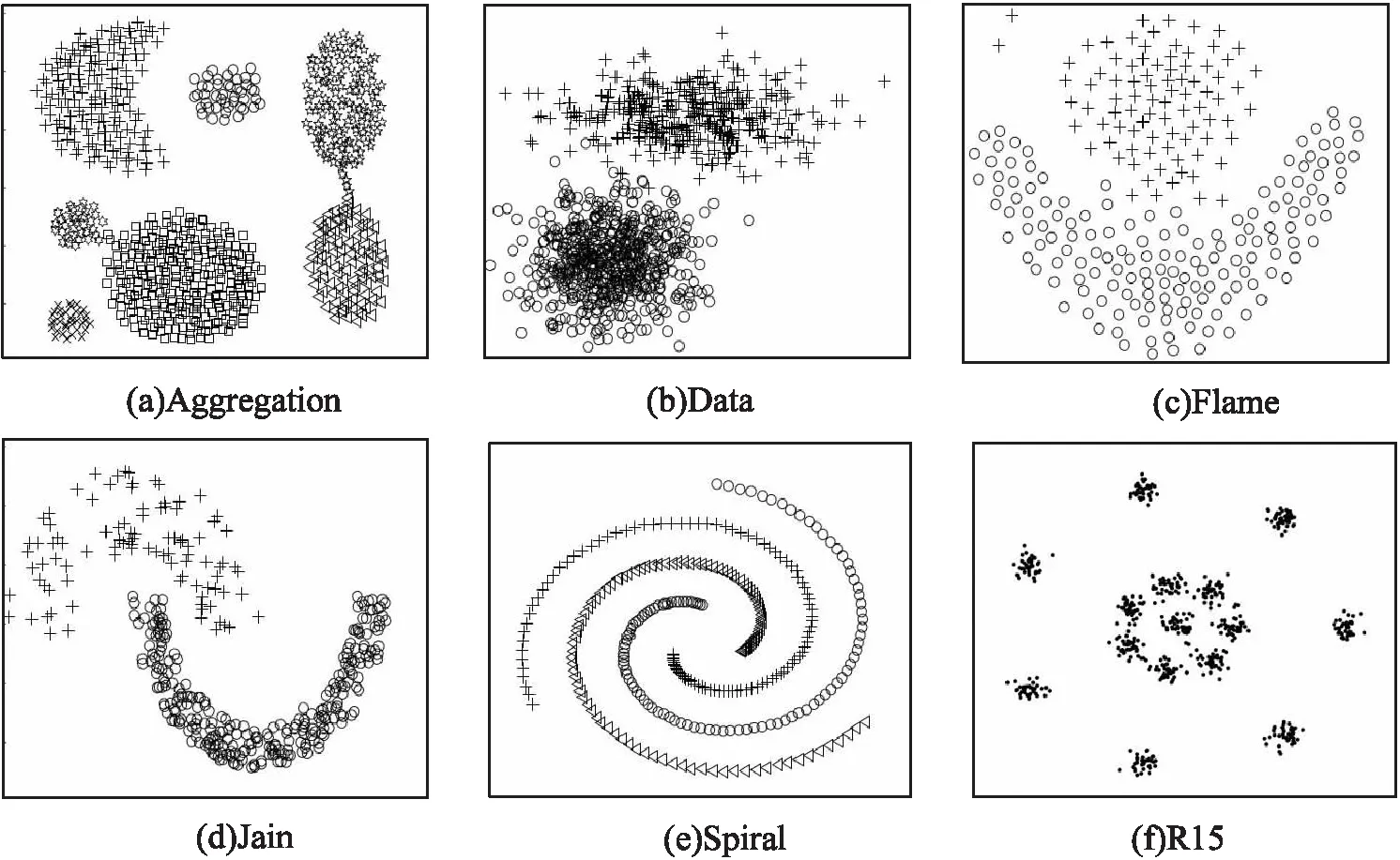
图1 原始数据集分布
(2)二维数据聚类效果。
为验证改进算法的有效性,分别使用DPC算法和改进算法进行实验,对比结果如图2所示。图2第一列为DPC算法结果,第二列为改进的DPC算法结果。其中将DPC算法中的截断距离阈值P均设置为0.01,簇类个数与真实数据保持一致。改进算法的截断距离dc均可自适应取得,簇类个数与真实数据保持一致。观察可得除了第四组数据集Jain以外,改进算法的聚类结果与原始分布更加吻合。
为了进一步验证文中算法的可靠性,选用精确度(ACC)、F测度(FM)和兰德系数(RI)三个有效性指标对算法结果进行量化分析,三个指标值越大,聚类效果越好。表2给出了6个数据集在DPC算法和文中改进算法下的指标值,综合比较可知改进算法有效性指标值更佳。
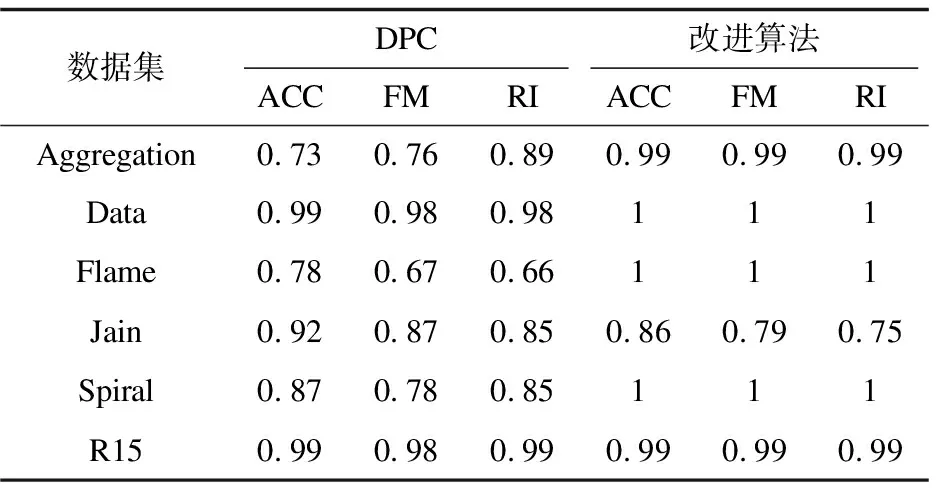
表2 不同数据的有效性指标
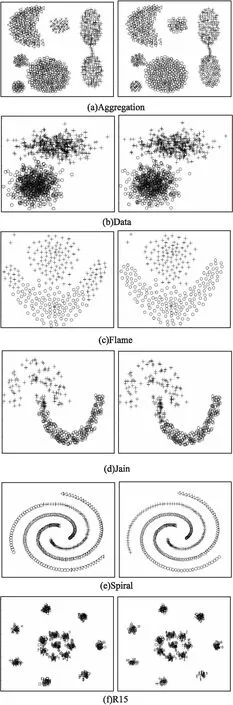
图2 原始数据集分布
3.3.2 数字图像分割效果
为验证文中算法能够较好地应用于图像分割,使用改进算法对数字图像数据集进行分割。将文中算法与K-means、FCM、DPC和文献[5]中的算法进行对比,验证改进算法具有较高的分割精度,对比算法的分割结果如图3所示。K-means、FCM、DPC和文献[5]中的算法需要确定簇类个数,且运行时间会随着类簇个数的增加而增加,而文中算法平均耗时为8秒,无论分割的簇类数有多大,运行时间基本不会发生改变,且文中算法的分割结果同GroundTruth更贴近,更能够清晰地分割图像边缘轮廓,将感兴趣的目标同背景分离。
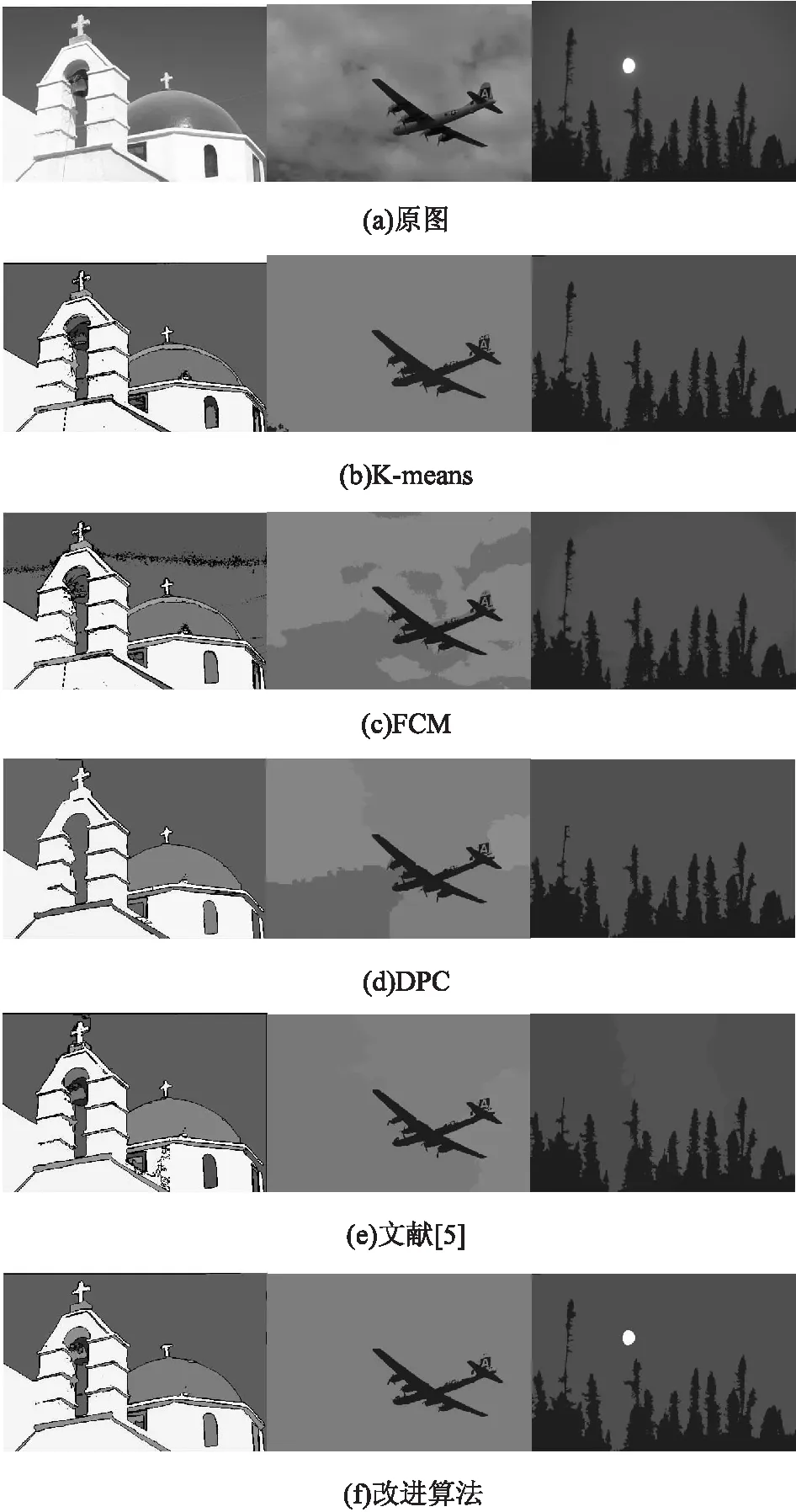
图3 不同算法分割结果
由图3可知,上述算法均能对数字图像进行分割。但在细节方面,K-means和FCM算法会出现过分割的现象,即冗余区域过多,导致本应属于同一区域的像素点被冗余的分割线条划分开,DPC算法和文献[5]中的算法错误分割较多。四种对比算法下的分割结果,均会导致颜色变化并不突兀的地方出现了过多冗余线条。而改进算法的分割得到图像轮廓与GroundTruth更加贴近,每个独立目标中的小区域很少,提取的轮廓界限也更加清晰可见。
作为较为经典的聚类算法,K-means比原始的DPC算法在图像分割上具有更明显的分割精度,然而无论是K-means、FCM、DPC还是文献[5]中的算法,均无法合理地选取簇类个数,这也是传统的聚类方法面临的统一难题。通过横向对比发现,改进算法具有较强的稳定性,从三个评价指标来看,改进算法均具有较强的优越性,无需确定任何参数,便可自适应地进行较为理想的图像分割。计算图3中的3幅图像PRI、VOI和USE三个指标平均值,指标数据如表3所示。
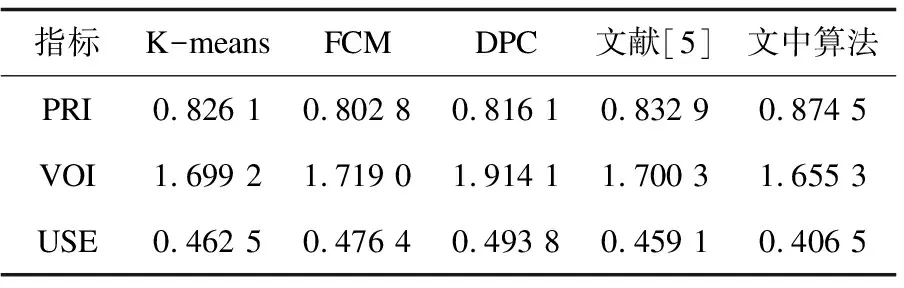
表3 各指标比较
4 结束语
针对DPC算法对参数敏感的问题,对截断距离dc进行自适应选取,并将改进的算法应用于图像分割。为解决DPC算法难以处理较大图像的问题,提出了分块并行的解决思路,并根据图像各区域内聚程度提出自适应获取数字图像簇类个数的方法。实验表明,该算法不但对二维数据有较好的聚类效果,而且能够适用于图像分割。
