挖掘知识关联整合教材设计构建学习生态链

2022-05-29倪方友

云南教育·中学教师 2022年4期

倪方友

义务教育教科书初中数学教材是教学的重要资源.在教学活动中，教师应深入研读教材，将教材中的例、习题进行整合，找到它们之间的关联点，挖掘初中数学知识间的内在联系，培养学生的思维能力，帮助学生形成学习生态链，构建知识网络，让学生对数学知识的理解水到渠成.下面笔者以“直线和圆的位置关系”章节中三角形内切圆部分的例、习题整合为例进行阐述.

一、题例分析，明确题目价值

义务教育教科书（人教版）《数学》九年级（上册）第二十四章24.2.2直线和圆的位置关系，讲解了切线长定理和三角形的内心相关内容.教材用三角形内切圆的圆心定义了三角形的内心，即三角形内切圆圆心是三角形三条角平分线的交点.在教学过程中，教师既要让学生对照图形理解三角形内切圆的概念，又要引导他们把三角形的内心和三角形的外心、内切圆和外接圆进行比较，让学生真正理解“切”和“接”的含义.

在教学中，要对教科书中的例、习题进行整合，我们首先应选中并深入分析一些题目.三角形内切圆部分有三道题目（包含例题与习题）引起了笔者的重视.在教学前，笔者深入分析了这几道题目的价值.

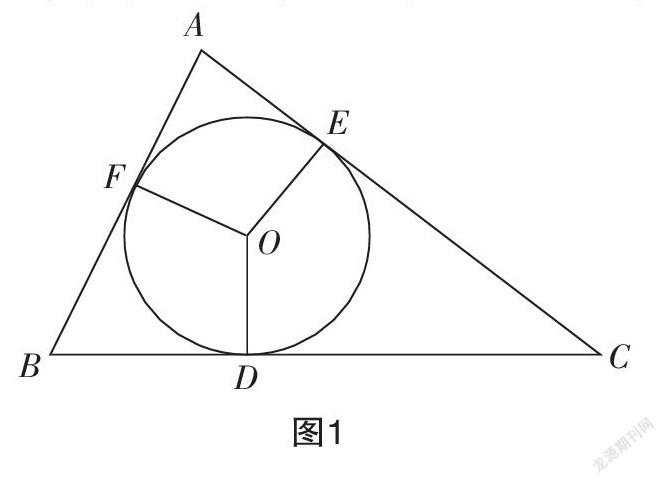
题目1：如图1，△ABC的内切圆☉O与BC，CA，AB分别相切于点D，E，F，且AB=9，BC=14，CA=13.求AF，BD，CE的长.

分析：这是教科书中出现的一道例题，设置该题的目的是为了巩固三角形内切圆与切线长定理，让学生加深理解，并获得新的解题方法.题目涉及一次方程，渗透了方程思想，可以通过建立方程或方程组进行解答：设AE=AF=x，则BF=BD=9-x，CD=CE=13-x，通过BC=BD+CD=14，建立一元一次方程（9-x）+（13-x）=14，从而求解.这也是教科书上采用的方法.因为△ABC的内切圆把其三边分成了三部分相等的线段，故也可以设AE=AF=x，BF=BD=y，CD=CE=z，建立一个三元一次方程组求解.当然，教科书中的解答方法较为简洁，必须让学生牢固掌握.

题目2：△ABC的内切圆半径为r，△ABC的周长为l，求△ABC的面积.（提示：设△ABC的内心为O，连接OA，OB，OC）

分析：这是教科书上的一道练习题，设置该题的目的是引导学生进一步理解三角形内切圆的半径，也能拓展三角形内心与面积关系的知识.教师可引导学生画出如图2所示图形，通过把△ABC分割成三个小三角形再面积求和即可求解.这道题不但渗透了整体分割成部分的转化思想和整体思想，还让学生获得了求三角形的面积的另一种方法.

题目3：如图3，Rt△ABC中，∠C=90°，AB，BC，CA的长分别为c，a，b.求△ABC的内切圆半径r.

分析：这是教科书设置的一道“拓广探索”练习题，解答略有难度.设置该题的目的是对三角形内切圆知识和三角形面积求法在特殊三角形中的应用，揭示了由一般到特殊的探究方法.解答时，我们要连接圆心与切点，把三角形分成三个小三角形，利用等积变换，列出方程求解.该题是对三角形内切圆相关知识的进一步拓展，通过自主探索，学生可以获得求三角形内切圆半径的一种方法.

二、关联挖掘，探究知识的内在联系

关联一：由题目1可以想到，已知△ABC的三边，可以求出△ABC的面积，运用八年级所学勾股定理建立方程即可;也可以运用八年级（下册）第十六章阅读与思考中的“海伦-秦九韶公式”.

关联二：利用题目2的结论S=rl，可以求出△ABC的内切圆半径r，从而得到结论：已知三角形的三边可以求其内切圆半径.

关联三：利用题目2的方法和结论S=rl，运用等积变换可以解决题目3，得到r=;也可以运用题目2的解题方法解答题目3，从而获得另一种解决路径和方法.

关联四：在解答题目3时，运用题目1和题目2的方法求出Rt△ABC的内切圆半径r的表达式虽不一样，但它们一定是相等的.从中我们发现了直角三角形内切圆半径的两种求法，进而推导出勾股定理.

三、整合设计，构建学生学习生态链

基于对教材及关联的分析，在对相关知识内容进行教学设计时，笔者尝试理清知识间的逻辑关系，进行整合设计，加强知识的纵横联系，提升学生的思维能力，帮助学生构建自己的学习生态链.

活动一：例题剖析

问题1：如图4，△ABC的内切圆☉O与BC，CA，AB分别相切于点D，E，F，你能得到什么结论？

结论1：由切线的性质可得OD⊥BC，OE⊥AC，OF⊥AB;

結论2：由切线长定理可得AE=AF，BF=BD，CD=CE;

结论3：由☉O的半径相等得OD=OE=OF;