一种基于目标空间转换权重求和的超多目标进化算法

梁正平 骆婷婷 王志强,2 朱泽轩 胡凯峰

现实应用中存在各种各样的多目标优化问题(Multi-objective optimization problems,MOPs),如电能分配[1]、污水处理控制[2]、服务质量优化[3]、车辆路径规划[4]、软件项目管理[5]、微电网管理[6],等等.由于MOPs 的不同目标函数之间通常相互冲突,MOPs 的最优解集不是单一的解而是一组折衷解,即帕累托最优解集(Pareto optimal set).虽然一些性能优越的多目标进化算法(Multi-objective evolutionary algorithms,MOEAs),如NSGA-II[7],SPEA2[8]和MOEA-PPF[9]等能很好的处理MOPs,但在解决超多目标优化问题(Many-objective optimization problems,MaOPs)时,上述算法的性能将显著下降.原因是随着目标函数的增加,非支配个体在种群中所占的比例将呈指数式增长,基于帕累托关系的算法会逐渐丧失收敛压力[10].为解决该问题,学术界从不同角度对超多目标进化算法(Manyobjective evolutionary algorithms,MaOEAs) 进行了较广泛的探讨[11-15],大致可分为以下四类:1) 基于放松支配.该类算法的主要思想是通过扩大支配范围来增强种群往PF 方向收敛的压力.代表性方法有ϵ支配[16],L支配[17]和模糊支配[18-19]等;2) 基于指标.该类算法将个体的指标值作为环境选择的衡量标准,如IBEA[20],HypE[21]和ARMOEA[22]等;3) 基于分解.该类算法将MaOPs 分解为多个单目标优化问题(Single-objective optimization problems,SOPs)[23],随后在进化框架下同时优化这些SOPs,如MOEA/D[24],NSGAIII[25]和SPEAR[26]等.4)混合型.该类算法采用两种或者两种以上的方法来实现对超多目标问题的优化,如Two_arch2[27]和HpaEA[28]均融合了基于支配和基于指标的方法,SRA[29]则采用了多指标的策略.在上述算法中,基于分解的MaOEAs 受到了学术界的高度关注,该类算法的核心是对参考向量和分解方法的设计.

参考向量主要影响种群在PF 上分布的均匀性,即多样性.在经典的分解类算法MOEA/D 中,采用一组均匀分布在目标空间上的向量集作为参考向量.该参考向量在规则PF 问题上能取得优越的性能,但不能很好地处理退化、不连续、凹凸混合等不规则PF 问题.原因在于不规则PF 上参考向量的分布不均匀,进而造成种群在PF 上分布不均匀.针对该问题,学术界提出了很多对均匀分布的参考向量进行调整的方法,如CA-MOEA[30]通过层次聚类方法来调整每代的参考向量,MOEA-AWA[31]则根据种群中的精英个体来对参考向量进行调整,类似的调整方法还有g-DBEA[32]和DDEANS[33]等.然而,由于频繁调整参考向量,参考向量调整类算法的性能在处理规则PF 问题时容易恶化[34].

分解方法主要影响种群的搜索效率,即收敛性.现有研究表明[35-37],切比雪夫方法可有效处理各种PF 形状的问题但搜索效率很低,权重求和方法虽然不能处理好非凸PF 问题但搜索效率却很高.为此,Ishibuchi 等提出了两种改进方案,分别为自适应切比雪夫和权重求和方法AS[37],同时使用切比雪夫和权重求和方法SS[38],以综合切比雪夫和权重求和各自的优势.此外,Wang 等提出了局部权重求和方法LWS[39],在综合性能上取得了显著的效果.但由于LWS 加入了局部的思想,一定程度上降低了权重求和方法的搜索效率.

总体而言,虽然学术界已对基于分解的MaOEAs进行了较广泛研究,但该类方法的性能仍存在较大提升空间.为尽可能不损害权重求和方法搜索效率高的优势,同时又能处理好各类PF 为非凸型的问题,本文从改进现有分解方法的角度,提出了一种基于目标空间转换权重求和的超多目标进化算法,简称NSGAIII-OSTWS.其中目标空间转换权重求和(Objective space transformation based weighted sum,OSTWS)将各种类型问题的PF 转换为凸型曲面,再利用权重求和方法对问题进行优化.具体地,首先利用预估PF 的形状计算个体到预估PF 的距离;然后,根据该距离值将个体映射到目标空间中预估凸型曲面与理想点之间的对应位置;最后,采用权重求和函数计算出映射后个体的适应值,据此实现对问题的优化.为验证OSTWS的有效性,本文在NSGAIII 框架的基础上,将OSTWS 与现有的7 个分解方法在WFG、DTLZ 和LSMOP 测试问题集上进行了对比,同时将所提的NSGAIII-OSTWS 与9 个具有代表性的MaOEAs 进行了对比,实验结果表明NSGAIII-OSTWS具备良好的竞争性能.

本文的内容安排如下.第1 节介绍与本文相关的背景知识.第2 节阐述目标空间转换权重求和方法OSTWS,以及基于OSTWS 的超多目标进化算法NSGAIII-OSTWS.第3 节介绍实验设计、实验结果,并进行相关讨论.最后对本文进行总结并指出未来的研究方向.

1 背景知识

1.1 多目标优化问题

一般来说,一个MOP 的数学定义可表述为:

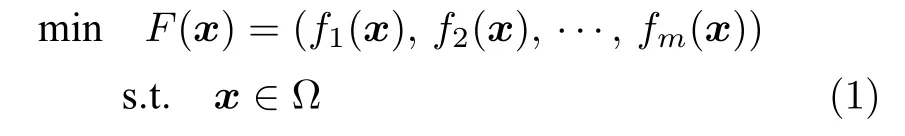
其中,x是决策空间 Ω 中的n维决策向量,m是目标函数的个数,Rm是目标空间.F:Ω→Rm组成m个目标函数.目标数m大于3 的MOPs 也被称为超多目标优化问题,即MaOPs.假设x和y是决策空间中的两个不同候选解,x支配y(记为x≺y) 当且仅当∀i∈{1,2,···,m},fi(x)≤fi(y) 且∃i ∈{1,2,···,m},fi(x)＜fi(y).如果候选解x不被任何其他解所支配,则称候选解x为帕累托最优解.所有帕累托最优解的集合称为帕累托最优解集(Pareto optimal set,PS),即PS={x/∃y ∈Ω,x ≻y}.所有帕累托最优解对应的目标向量构成帕累托最优前沿(Pareto optimal front,PF),即PF={F(x)|x ∈PS}.

1.2 分解方法

分解方法决定了基于分解的MaOEAs 的搜索效率,对算法的性能有着重要影响.研究者们设计了许多不同的分解方法,并在各种MaOPs 上展现出了优越的性能.常见的分解方法有以下三种:

1)权重求和(Weighted sum,WS)法:WS 方法通过加权的方式将所有目标组合成一个单一的目标,其数学定义如下:

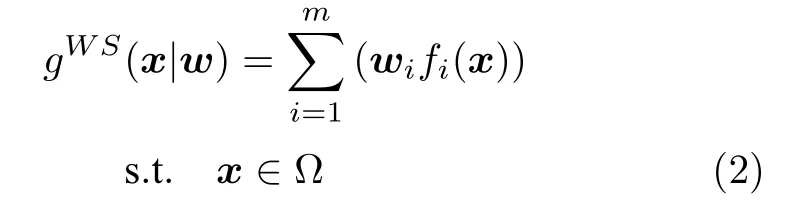
2)切比雪夫(Techebycheff,TCH)法:TCH 方法将MaOP 转化为一个SOP 的数学定义如下:

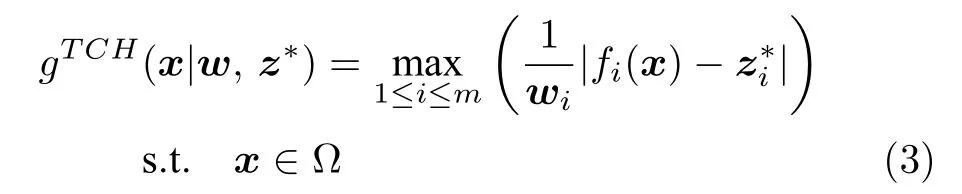
3)基于惩罚的边界交叉(Penalty-based boundary intersection,PBI)法:PBI 方法构造子问题的数学定义如下:

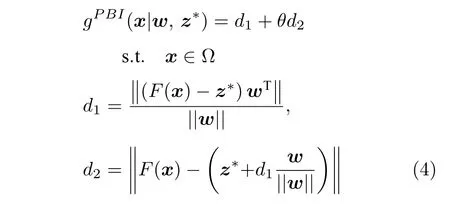
其中,θ(θ＞0) 为一个事先设定的惩罚因子,d1为向量 (F(x)-z*) 在权重向量w上的投影长度,d2为F(x)到w的垂直距离.图1(c)为PBI 方法的示意图.由PBI 的定义(式(4)) 和图1(c) 可知,θ是平衡收敛性(用d1衡量)和多样性(用d2衡量)的关键性参数.近来有研究表明[43-44],当PBI 处理PF为凸的问题时,较大的θ可以获得较好的种群分布,而较小的θ值有利于种群更好地收敛到PF.

图1 分解方法WS,TCH 和PBI 在参考向量w 上的二维示意图,其中虚线为等高线Fig.1 Illustration of the decomposition methods WS,TCH and PBI on reference vector w,where dashed lines are contour lines

2 NSGAIII-OSTWS 算法

2.1 动机

在基于分解的算法中,分解方法将MaOP 转化为若干个SOPs,然后在进化框架下以协同的方式优化每个SOPs.如果没有选择合适的分解方法,或者使用的分解方法不能很好地将MaOP 转化为SOPs,基于分解的MaOEAs 最终获得的种群就有可能无法逼近PF.

目前,上节介绍的三种分解方法,即WS、TCH和PBI,已在基于分解的MaOEAs 中被广泛应用.图1 是这三种方法在二维目标空间下的示意图.每个子图中的等高线将目标空间划分为两个区域,位于同一条等高线上的解具有相同的质量,靠近理想点z*区域的解质量则要优于另外一区域.如图1(a)所示,WS 的等高线是一条经过候选解且垂直于参考向量的直线,其优越区域[39]占整个区域的1/2.从图1(b)可以看出,TCH 的等高线则为经过候选解和参考向量的两条相互垂直的直线,其优越区域为 1/ 2m,随着目标函数m的增加,该值会显著减小.图1(c)中,PBI 的等高线是经过候选解和参考向量的两条相交直线,它的优越区域由惩罚因子θ决定.θ值越大,则优越区域的面积越小,通常情况下该区域的面积小于整个区域面积的1/2.由上述分析可知,WS 的优越区域是最大的.换言之,采用WS 可以更大概率搜索到比目前更优的解,即收敛速度最快.然而,当采用WS 处理非凸问题时,PF 中的大部分点会被丢失[24],从而严重损失种群的多样性[39].综上所述,相比TCH 和PBI 而言,WS 具有更强的收敛性但却不能处理好非凸问题.

为充分发挥WS 搜索效率高的优势,同时又能处理好各类PF 形状为非凸的问题,研究者们提出了一些WS 的改进方法,如AS[37]和SS[38]等.然而,这些方法的主要思想仅是利用TCH 方法来处理WS 不能处理好的凸型PF 问题,并未对WS 方法本身进行改进.最近,Wang 等[39]提出了一种新颖的WS 方法,即局部权重求和方法LWS.该方法的主要思想是对于每个搜索方向,只在其相邻解中挑选最优解.LWS 方法能够较好处理包括PF 非凸在内的各类型PF 问题,但由于LWS 在求解最优解时加入了局部的思想,也在一定程度上降低了WS方法搜索效率高的优势.为验证该结论,本文将LWS 方法和WS 方法分别嵌入到基于分解的算法NSGAIII[25],形成算法NSGAIII-WS 和NSGAIIILWS.图2 为这两个算法在PF 为凸的测试问题ZDT1[45]上的最终种群分布图.其中,运行次数为20 次,迭代次数为120 代,种群大小为200,决策变量数的大小参照文献[45]设置,其它参数与NSGAIII保持一致.从图2 可以看出,NSGAIII-WS 算法获得的种群具有更好的收敛性.为尽可能发挥权重求和方法搜索效率高的优势,同时又能处理好非凸型PF 问题,本文提出了一种新颖的方法——目标空间转换权重求和方法.

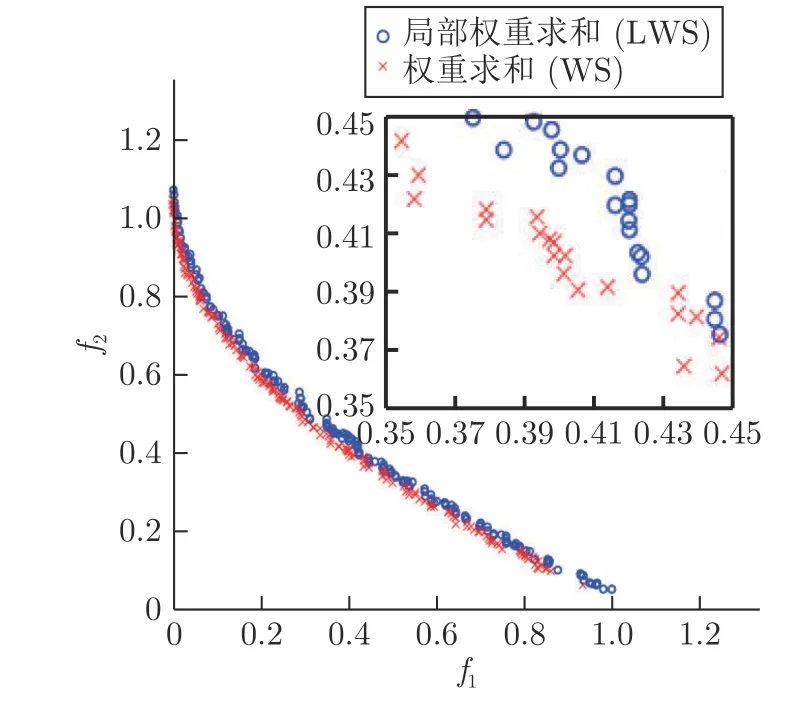
图2 NSGAIII-WS 和NSGAIII-LWS 算法在ZDT1上获得的最终种群分布Fig.2 The final population distribution obtained by NSGAIII-WS and NSGAIII-LWS algorithm on ZDT1

2.2 目标空间转换权重求和方法

目标空间转换权重求和方法OSTWS 的核心思想,是将各种问题的PF 转换为凸型曲面,并基于该凸型曲面进行求解.OSTWS 方法的伪代码如算法1 所示.

首先,采用NSGAIII[25]中的归一化策略对种群U进行归一化处理,然后利用2REA[46]中的估PF 方法预估出PF 的形状.种群归一化的目的是维持种群的多样性.在进化前期,由于种群中的大部分个体并未收敛到PF,归一化会存在较大的误差,但在进化后期,大部分个体都已靠近或收敛到PF,此时种群归一化所带来的误差会逐渐降低.预估的过程是先选取一组候选曲率p值逐一计算种群中非支配个体到理想点的Lp范式值,并据此计算出各p值所对应的标准方差.方差越小,代表该p值所对应的曲面越能拟合当前种群的分布.最终选取具有最小方差的p值所对应的曲面作为预估的PF 形状.之后,将种群中的所有个体映射到所预估的PF 上,映射公式如下:

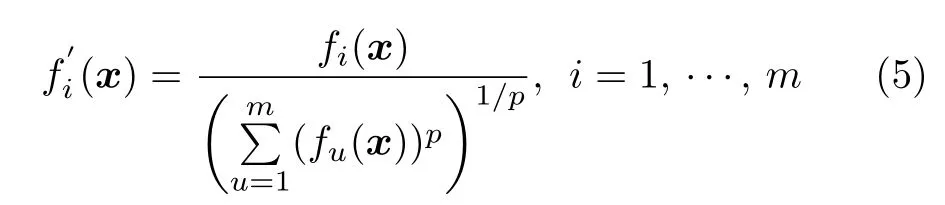
接下来,以原点作为理想点,分别计算原始个体与映射个体到理想点之间的欧氏距离值d1(x)和d2(x),并将d1(x) 减去d2(x),以此得到目标空间转换所需的距离值d(x).随后,根据d(x)值将个体转换到目标空间中凸曲面与理想点之间对应的位置,从而完成目标空间的转换.具体的做法是以等距离d(x)的形式将原始种群中的所有个体映射到预设的凸曲面内.预设凸曲面的定义如下:

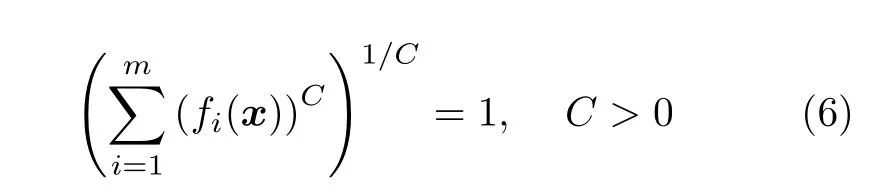
其中,[f1(x),f2(x),···,fm(x)]为预设凸曲面上的一个向量,C为预设凸曲面的曲率值,种群中个体映射到预设凸曲面内的数学公式如下:

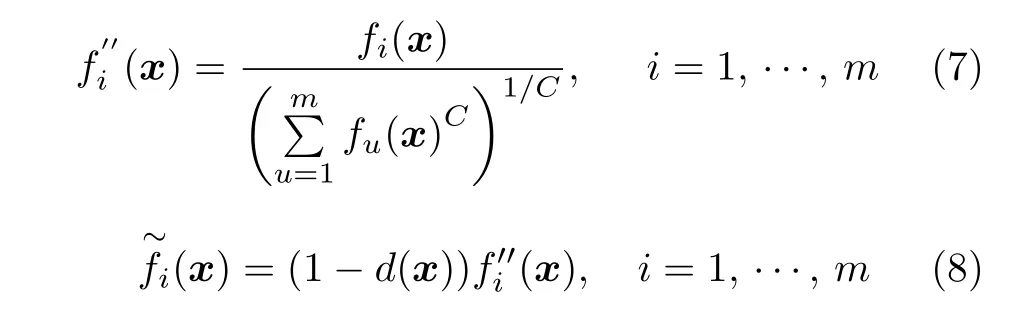
最后,将最小化求解问题转化为最大化求解问题并采用WS 方法计算出目标空间转换后个体的适应值,适应值越大代表个体越优秀.

为更直观地展示OSTWS 方法,图3 示例了使用OSTWS 方法将线形、凸形和凹形PF 中的个体转换到凸目标空间的整个过程.以3(a)为例,首先,预估出真实PF 的形状(直线),并将种群中的所有个体(a,b,c)映射到直线上(a＇,b＇,c＇),然后计算出原始个体(a,b,c)与映射后个体(a＇,b＇,c＇)之间的欧氏距离值d1,d2,d3.值得注意的是,距离值(d1,d2,d3)具有正负之分,如果原始个体到理想点的欧氏距离大于映射后个体到理想点的欧氏距离,则上述距离值为正,否则为负.接下来,将原始种群中的所有个体(a,b,c)以等距离 (d1,d2,d3)形式映射到预设凸曲线内,完成种群到凸目标空间的转换,转换后的个体为a′′,b′′,c′′.最后,采用WS方法逐一计算个体(a′′,b′′,c′′) 的适应值,适应值越大的个体被挑选到下一代进化过程中的概率也越大.

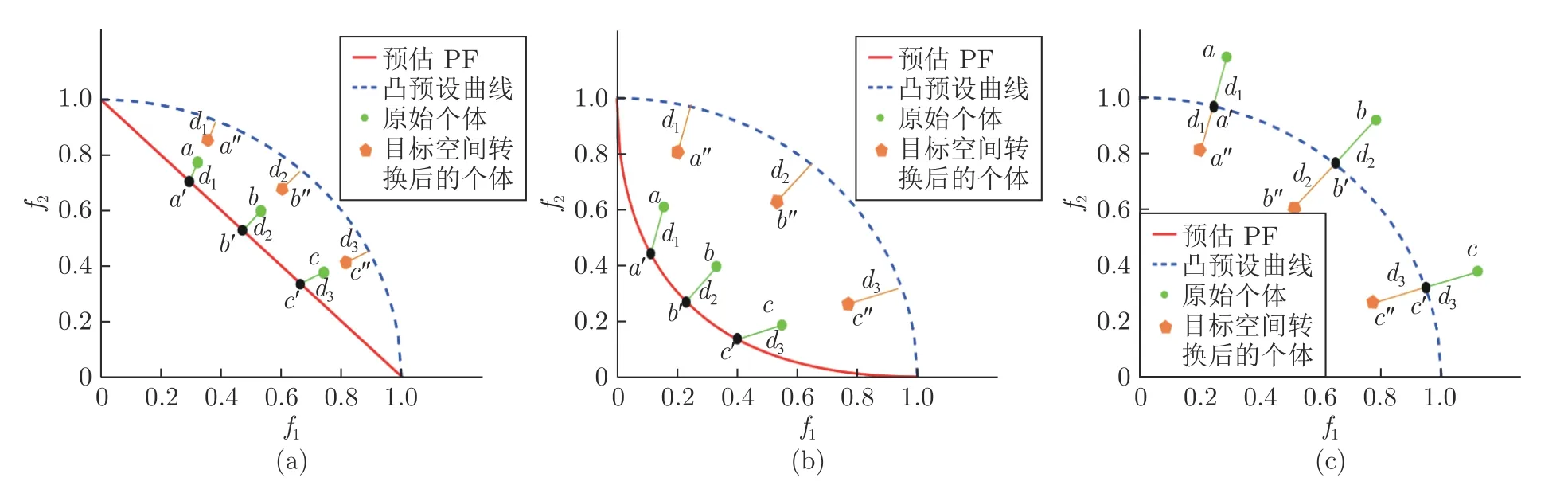
图3 OSTWS 方法将PF 形状为线形(a),凸形(b)和凹形(c)种群中的个体转换到凸目标空间的整个过程Fig.3 The whole process of transforming the population individuals from linear (a),convex (b) and concave(c) into convex objective space by OSTWS method

2.3 将OSTWS 方法整合到NSGAIII 中

在进化算法领域,MOEA/D 和NSGAII 是两个基于分解的经典算法,NSGAIII 则是NSGAII 在高维目标空间下的改进版.相比MOEA/D,NSGAIII 专门针对MaOPs,且在高维空间下能够更好地维持种群的多样性[25,47-48].为公平比较各种分解方法在处理MaOPs 时的有效性,本文选择NSGAIII作为基础算法,并将OSTWS 方法嵌入NSGAIII形成新的算法NSGAIII-OSTWS,算法2 为其伪代码.首先,初始化规模为N的种群U和参考向量W,然后对种群U进化过程,直至算法达到最大迭代次数.

算法2.NSGAIII-OSTWS 算法

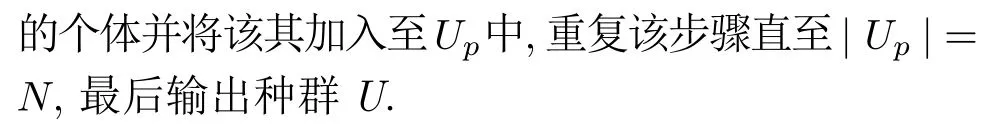
2.4 时间复杂度分析

时间复杂度是衡量算法性能的一个重要方面,影响算法的整体计算开销.下面根据NSGAIII-OSTWS 的主要流程对其时间复杂度进行详细分析.算法2 第4 行的子代个体生成中,二进制交叉和多项式变异需要O(DN)的计算开销,其中D为决策变量的数量.算法2 第6 行对规模为2N的种群进行非支配层排序要花费O(Nlogm-2N)[25]的计算代价.算法2 第15 行,即算法1,其计算开销包括以下四方面:1) 将规模为2N的种群进行归一化(算法1 第1 行),需要O(mN) 的计算开销.2)计算出2N个个体到预设曲面的距离(算法1 第4～7行),需要O(mN) 的计算开销.3) 将2N个个体的目标空间转换到特定曲面内(算法1 第8～9 行),需要O(mN)的计算开销.4)计算目标空间转换后2N个个体到参考向量W的权重求和值(算法1 第10～12 行),需要O(mN|W|) 的计算开销,其中|W|是参考向量的个数.因此,算法1 的时间复杂度为O(mN|W|).之后,在最坏情况下NSGAIII-OSTWS 需对2N个个体进行参考向量的归属,此时需要花费O(mN|W|) 的计算代价.最后,NSGAIIIOSTWS 需挑选N-|Up |个个体至下一代进化过程需要O(L|W|) 的计算量,其中L=|Fl|.此外,在通常情况下,N≈|W|,N＞m.考虑到以上因素和计算结果,NSGAIII-OSTWS 的时间复杂度为Max(O(DN),O(mN|W|)).

3 实验与分析

3.1 实验设置

1) 测试问题和评价指标

为检验NSGAIII-OSTWS 的性能,本文选取了超多目标优化领域中使用最为广泛的两组测试问题集WFG[51]、DTLZ[52]和最新的大规模决策变量测试问题集LSMOP[53].在DTLZ 中,DTLZ8-9 为带约束的问题,因此本文只考虑对DTLZ1-7 问题的研究.参照文献[39],WFG 和DTLZ 中的决策变量数目统一设置为D=100,其中WFG 中的位置变量数设为k=m-1.LSMOP 的相关参数与原文[53]保持一致.

为定量评估算法的求解性能,分别采用世代距离(Generational distance,GD[54]),覆盖PF(Coverage over the pareto front,CPF[55]) 和修正的反转世代距离(Modified inverted generational distance,IGD+[56]) 进行收敛性、多样性和综合性(平衡收敛性和多样性的能力)性能衡量,其计算公式分别如下:

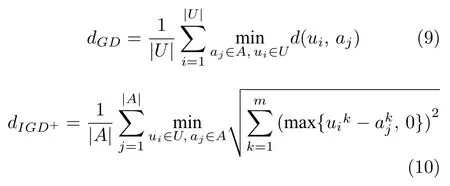
其中U为算法输出的最终种群,A为测试问题PF面上的一组均匀参考点.对于目标维度不相同的缩放问题(如:WFG),在计算GD 和IGD+指标之前需对A和U进行归一化处理[48].GD 和IGD+值越小,代表算法的性能越好.参照文献[57],本实验设置计算GD 和IGD+所需的参考点数为10 000.

2) 参数设置

由于分解算法的种群规模取决于参数H和m,其中H为沿每个目标轴所考虑的分区.为公平起见,本章所测试的目标维度及其对应的种群大小统一设置为表1 所示.为避免参考向量分布不均匀的情况,当m＞5 时,本文采用两层参考向量生成方法生成参考向量[58].交叉和变异操作所需的参数设置如表2 所示.在NSGAIII-OSTWS 中,曲率C值的参数经验设置为2,其影响在实验分析部分进行研究.比较算法的其他参数设置与其原始论文保持一致.所有算法的终止准则被指定为最大迭代次数(MAXGen),本文中所有测试问题的MAXGen 设为300.每个算法在每个测试问题上独立运行20 次.为检验算法性能的显著性差异,采用Wilcoxon[59]秩和检验来评估一种算法在GD 或IGD+值方面是否优于另一种算法.符号 “+”,“-” 和 “≈”表示相应的竞争算法在5%的显著性水平上分别比所提算法NSGAIII-OSTWS 更好,更差和无统计性差异.

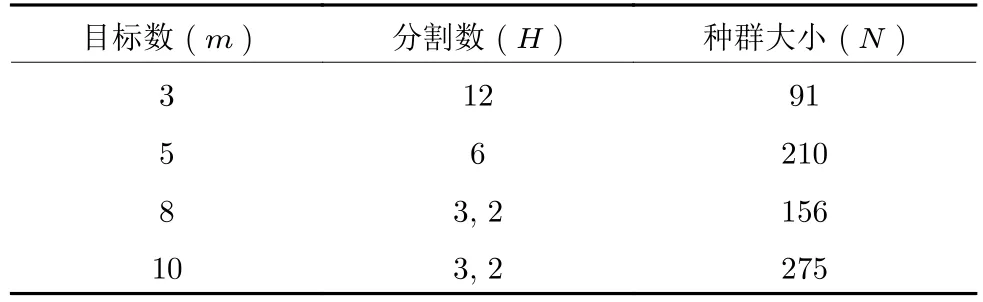
表1 种群大小设置Table 1 Setting of the population size

表2 交叉变异参数设置Table 2 Parameter settings for crossover and mutation

3.2 实验结果与分析

1) OSTWS 方法的有效性验证

为验证目标空间转换权重求和方法(OSTWS)的有效性,本小节将OSTWS 方法与其他7 个分解方法,即切比雪夫方法(TCH)、惩罚边界交叉方法(PBI[24])、局部权重求和方法(LWS[39])、自适应切比雪夫和权重求和方法(AS[37])、同时使用切比雪夫和权重求和方法(SS[38])、自适应Lp 方法(PaS[36]) 和自适应惩罚方法(APS[60]) 在算法NSGAIII 的框架上进行比较实验.表3、表4 和表5 分别统计了上述分解方法在DTLZ1-DTLZ7、WFG1-WFG9 和LSMOP1-LSMOP9 测试问题上所获得的GD 均值和标准差(括号内为标准差),其中每个问题的最佳结果以灰色背景突出显示.图4为各个算法在所有测试问题上的平均IGD+表现分,分值越小表示该算法整体性能越好.

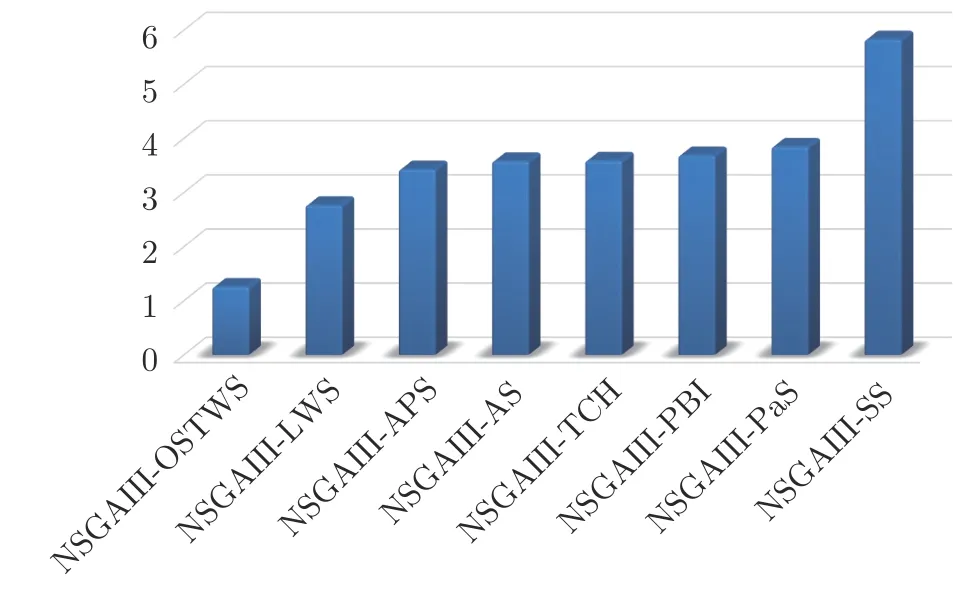
图4 NSGAIII-OSTWS,NSGAIII-LWS,NSGAIII-TCH,NSGAIII-PBI,NSGAIII-AS,NSGAIII-SS,NSGAIII-APS和NSGAIII-PaS,在所有测试问题实例中的平均IGD+性能得分排名.得分越小,整体性能越好Fig.4 Ranking in the average performance score over all test problem instances for the algorithms of NSGAIII-OSTWS,NSGAIII-LWS,NSGAIII-TCH,NSGAIII-PBI,NSGAIII-AS,NSGAIII-SS,NSGAIII-APS and NSGAIII-PaS.The smaller the score,the better the overall performance in terms of IGD+

由表3、表4 和表5 可以看出,NSGAIII-OSTWS 在绝大部分DTLZ 测试问题上都取得了最佳GD 均值,此外,虽然NSGAIII-OSTWS 没能在所有的WFG 和LSMOP 测试问题中获得最具竞争力的GD 性能,但总体上获得了最优的性能,这表明本文所提出的OSTWS 方法是非常有效的,原因在于充分利用了WS 方法搜索效率高的优势.

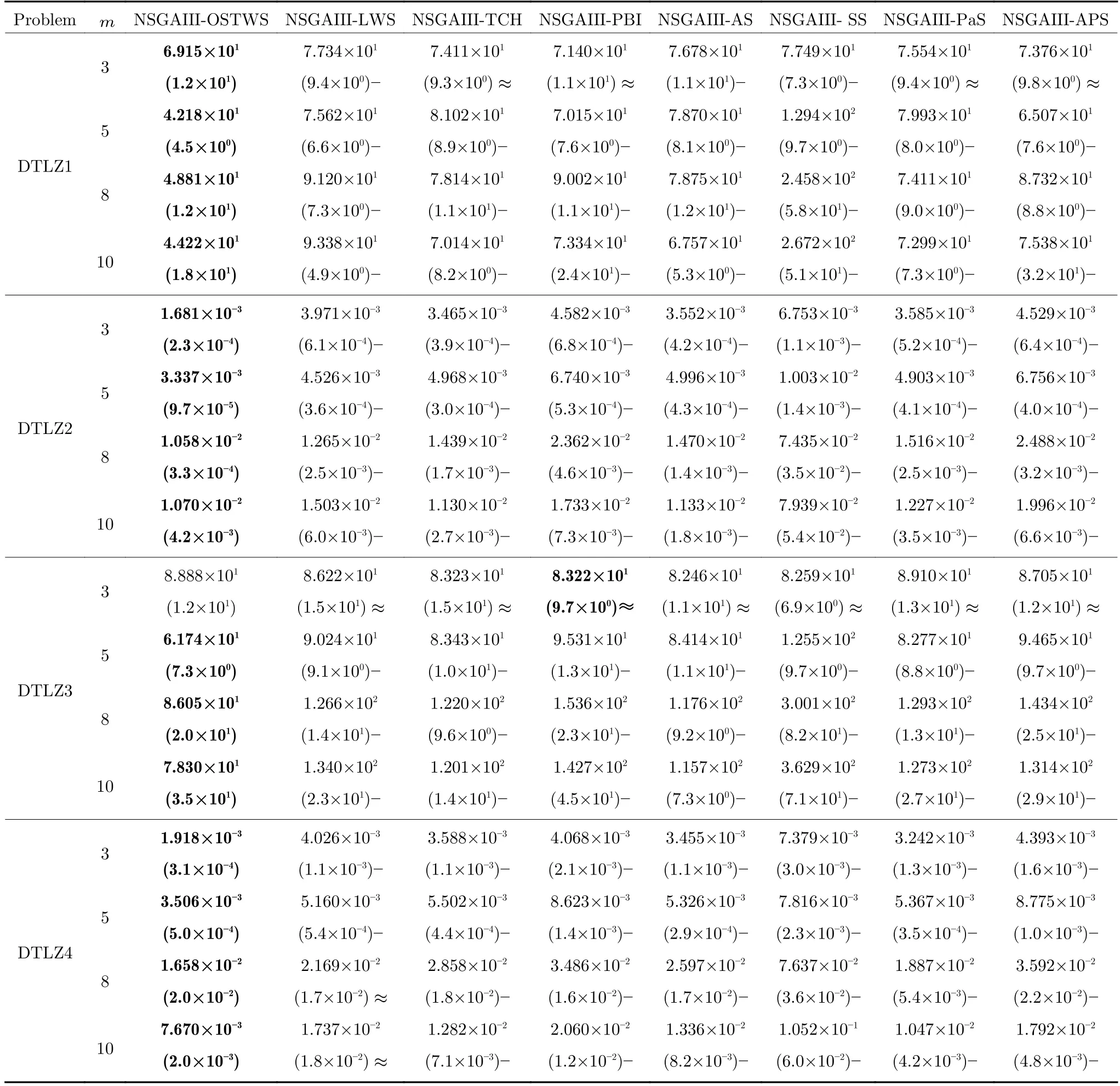
表3 OSTWS,LWS,TCH,PBI,AS,SS,PaS 和APS 方法在框架为NSGAIII,测试问题为DTLZ1-7 上获得的GD 值统计结果(均值和标准差).每个实例算法中的最好结果以加粗突出显示Table 3 The statistical results (mean and standard deviation) of the GD values obtained by OSTWS,LWS,TCH,PBI,AS,SS,PaS and APS methods on the NSGAIII framework and DTLZ1-7 test problems.The best average value among the algorithms for each instance is highlighted in bold

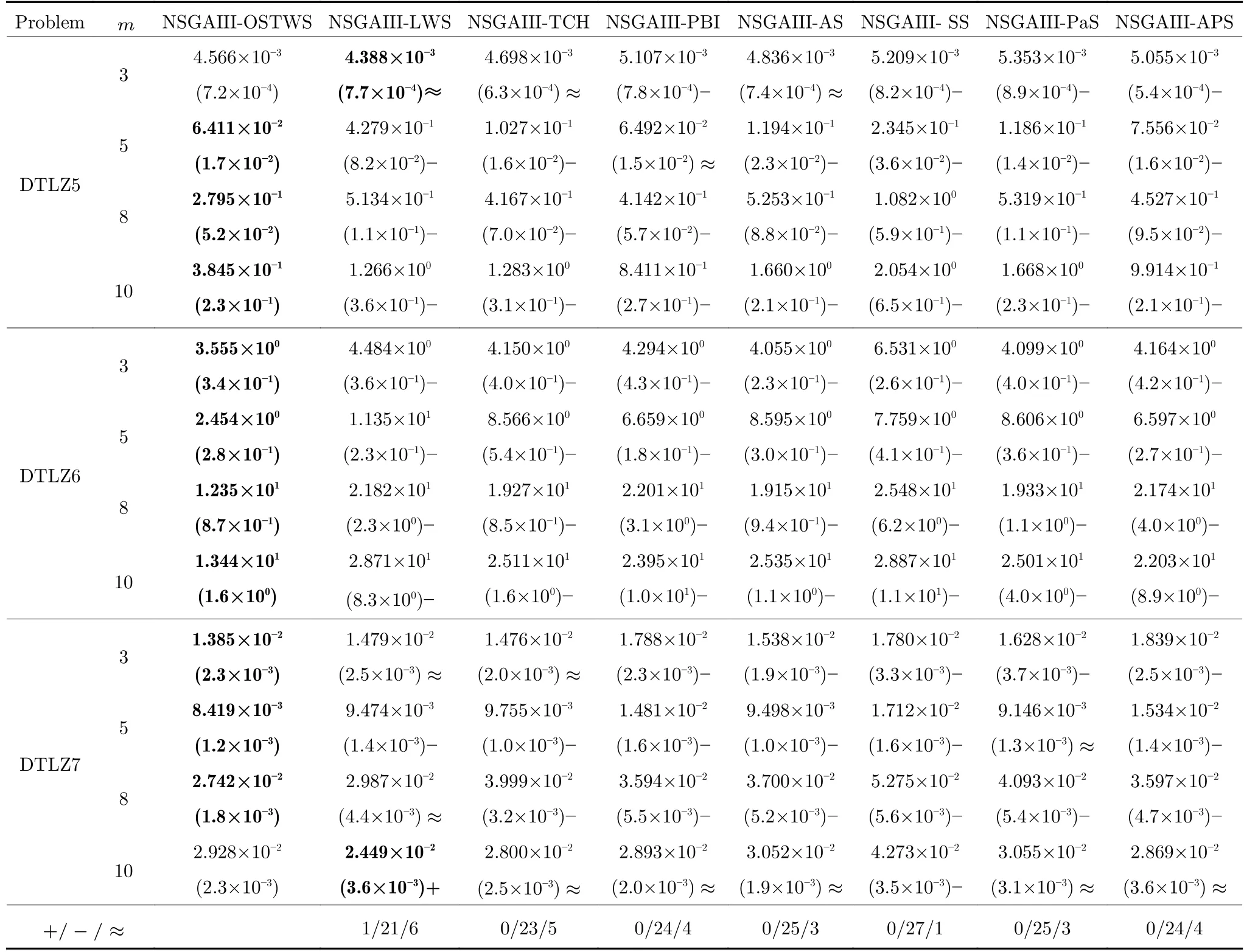
表3 OSTWS,LWS,TCH,PBI,AS,SS,PaS 和APS 方法在框架为NSGAIII,测试问题为DTLZ1-7 上获得的GD 值统计结果(均值和标准差).每个实例算法中的最好结果以加粗突出显示 (续表)Table 3 The statistical results (mean and standard deviation) of the GD values obtained by OSTWS,LWS,TCH,PBI,AS,SS,PaS and APS methods on the NSGAIII framework and DTLZ1-7 test problems.The best average value among the algorithms for each instance is highlighted in bold (continued table)

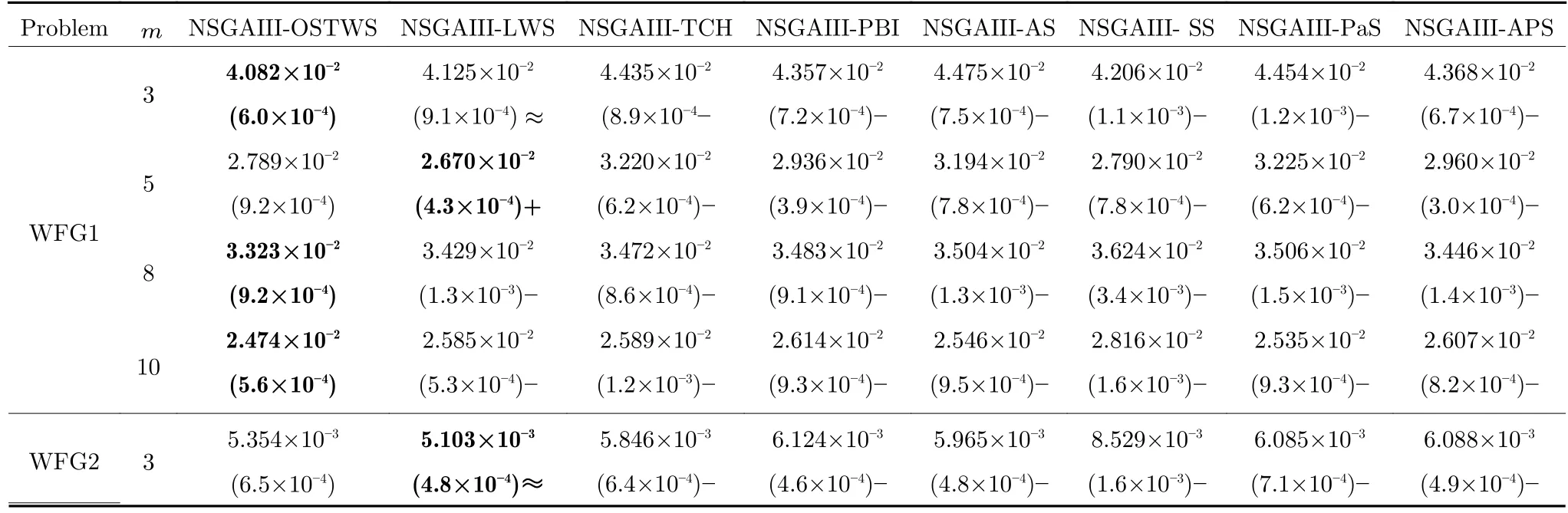
表4 OSTWS,LWS,TCH,PBI,AS,SS,PaS 和APS 方法在框架为NSGAIII,测试问题集为WFG1-9 上获得的GD 值统计结果(均值和标准差).每个实例算法中的最好结果以加粗突出显示Table 4 The statistical results (mean and standard deviation) of the GD values obtained by OSTWS,LWS,TCH,PBI,AS,SS,PaS and APS methods on the NSGAIII framework and WFG1-9 test problems.The best average value among the algorithms for each instance is highlighted in bold

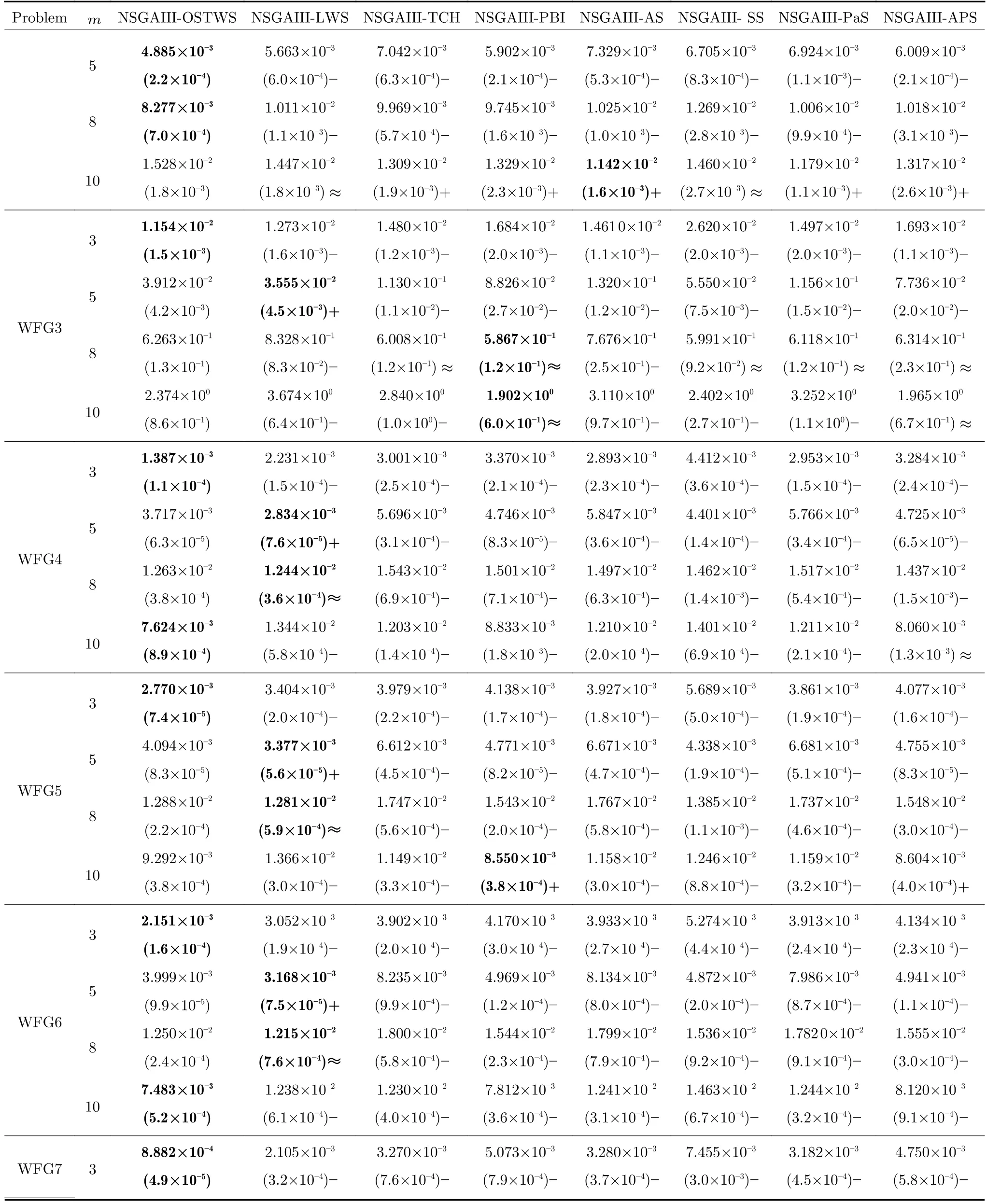
表4 OSTWS,LWS,TCH,PBI,AS,SS,PaS 和APS 方法在框架为NSGAIII,测试问题集为WFG1-9 上获得的GD 值统计结果(均值和标准差).每个实例算法中的最好结果以加粗突出显示 (续表)Table 4 The statistical results (mean and standard deviation) of the GD values obtained by OSTWS,LWS,TCH,PBI,AS,SS,PaS and APS methods on the NSGAIII framework and WFG1-9 test problems.The best average value among the algorithms for each instance is highlighted in bold (continued table)

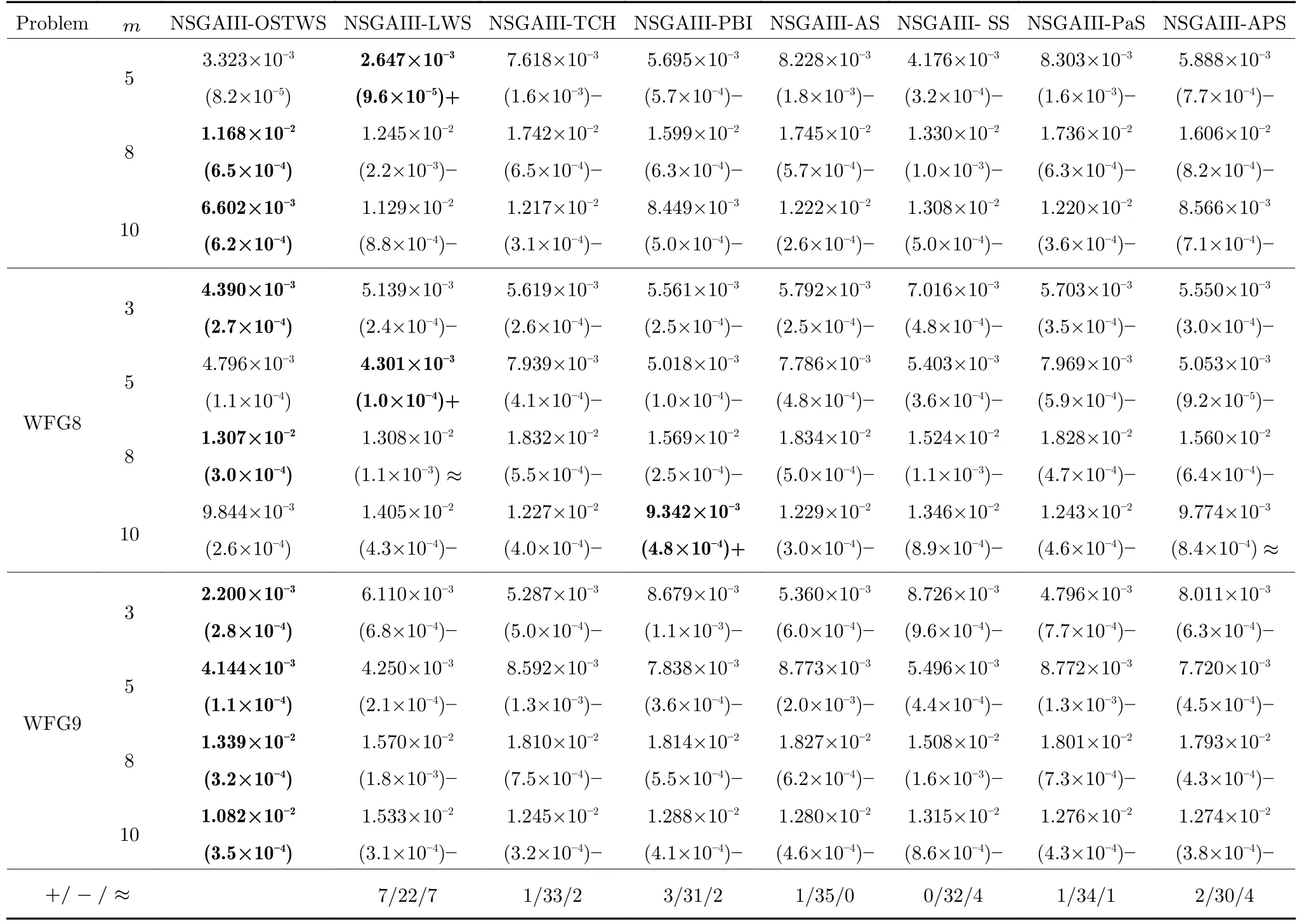
表4 OSTWS,LWS,TCH,PBI,AS,SS,PaS 和APS 方法在框架为NSGAIII,测试问题集为WFG1-9 上获得的GD 值统计结果(均值和标准差).每个实例算法中的最好结果以加粗突出显示 (续表)Table 4 The statistical results (mean and standard deviation) of the GD values obtained by OSTWS,LWS,TCH,PBI,AS,SS,PaS and APS methods on the NSGAIII framework and WFG1-9 test problems.The best average value among the algorithms for each instance is highlighted in bold (continued table)

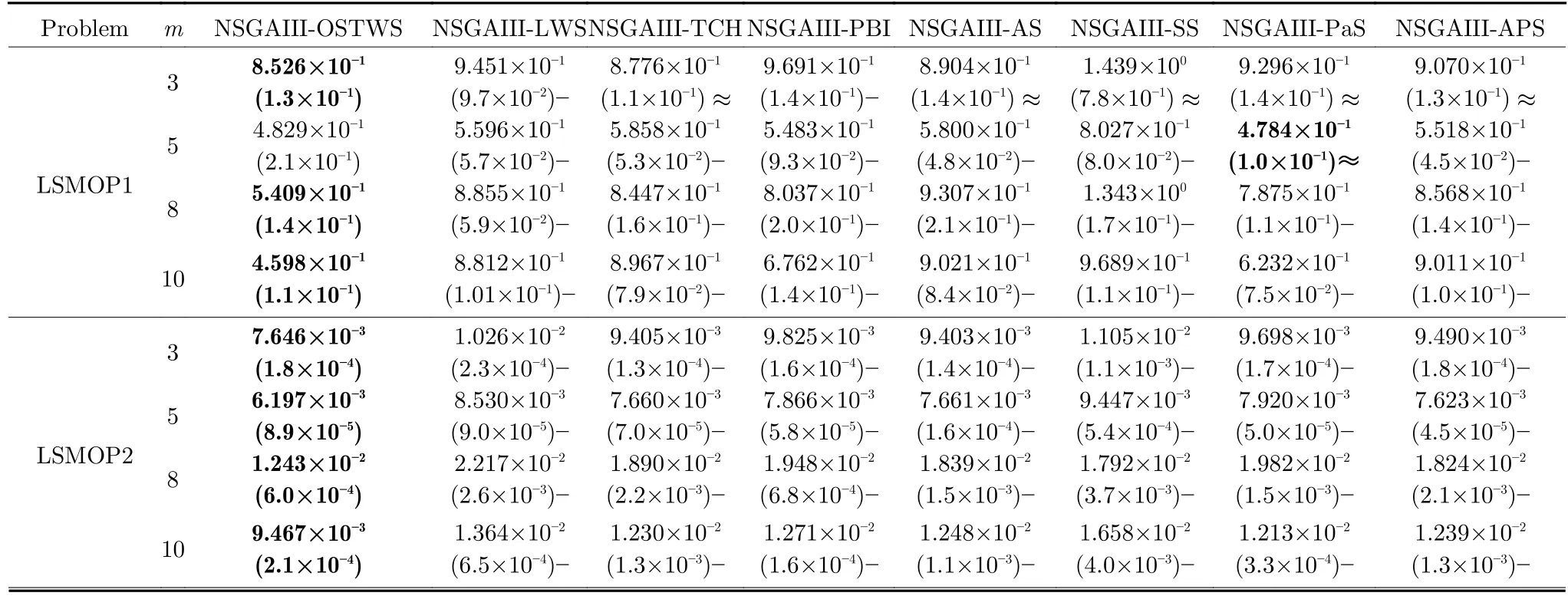
表5 OSTWS,LWS,TCH,PBI,AS,SS,PaS 和APS 方法在框架为NSGAIII,测试问题集为LSMOP1-9 上获得的GD 值统计结果(均值和标准差).每个实例算法中的最好结果以加粗突出显示Table 5 The statistical results (mean and standard deviation) of the GD values obtained by OSTWS,LWS,TCH,PBI,AS,SS,PaS and APS methods on the NSGAIII framework and LSMOP1-9 test problems.The best average value among the algorithms for each instance is highlighted in bold

表5 OSTWS,LWS,TCH,PBI,AS,SS,PaS 和APS 方法在框架为NSGAIII,测试问题集为LSMOP1-9 上获得的GD 值统计结果(均值和标准差).每个实例算法中的最好结果以加粗突出显示 (续表)Table 5 The statistical results (mean and standard deviation) of the GD values obtained by OSTWS,LWS,TCH,PBI,AS,SS,PaS and APS methods on the NSGAIII framework and LSMOP1-9 test problems.The best average value among the algorithms for each instance is highlighted in bold (continued table)

下面具体分析各个算法在DTLZ1-DTLZ7、WFG1-WFG9 和LSMOP1-LSMOP9 测试问题上的性能.DTLZ1 是一个线性问题,NSGAIII-OSTWS 在该问题上获得了最佳的GD 值,即在线性的DTLZ1 问题上,OSTWS 方法的收敛性要强于其它所对比的分解方法.DTLZ2-4 和WFG4-9 为凹问题,对于DTLZ2-4,NSGAIII-OSTWS 获得了最优性能.为直观展示各个算法在凹问题上的收敛性能,图5 例举了所有算法在10 维DTLZ2问题上的最终种群分布图.从图5 可以看出,算法NSGAIII-OSTWS 的种群分布在目标空间[0,1]内,其它算法的种群大部分都分布在目标空间[0,1.2]内,这表明算法NSGAIII-OSTWS 能很好的将种群收敛到PF 上,而其它算法却不能.虽然WFG4-9同样为凹问题,但相对于DTLZ2-4 来说,WFG4-9测试问题具有多峰、带欺骗和变量不可分离等更加复杂的特点,从而给算法带来了更大的挑战.但从表4 可以看出,NSGAIII-OSTWS 在大部分WFG4-9 测试问题上都能取得最佳的性能指标值.DTLZ5-6 和WFG3 为退化问题,对于DTLZ5-6,NSGAIIIOSTWS 仍然表现出了最佳的收敛能力.在WFG3上,由GD 指标的统计数据可知NSGAIII-OSTWS 的性能则一般.WFG1 是一个凹凸混合问题,WFG2 和DTLZ7 为不连续问题,在这三个问题上,NSGAIII-OSTWS 的性能会有所下降.原因是OSTWS 很难快速且准确地预估出此类PF 的形状,需要消耗一定的迭代次数,从而降低了种群的收敛速度.但本文所采用的预估PF 方法最终能较好地预估出这些问题的PF 形状,故在处理这些不规则测试问题时依然取得了较好的性能.相对于DTLZ和WFG 测试问题集,LSMOP 具有更大规模的决策变量,种群的收敛难度增大,对现有的超多目标算法提出了更大的挑战.由于OSTWS 继承了权重求和分解方法的高搜索效率,因此相对于原始的NSGAIII 算法,NSGAIII-OSTWS 在难收敛的大规模决策变量问题处理上仍具有显著的优势,能较快地将种群进化至PF.从表5 可以看出,本文所提出的算法NSGAIII-OSTWS 在LSMOP 的大部分测试问题上都取得了最佳的GD 指标值,这再次验证了OSTWS 方法具有很强的搜索效率.综合统计结果可以看出,NSGAIII-OSTWS 在DTLZ、WFG和LSMOP 测试集上虽然没能在每个测试实例上都获得最优的GD 结果,但总体收敛性能优异.

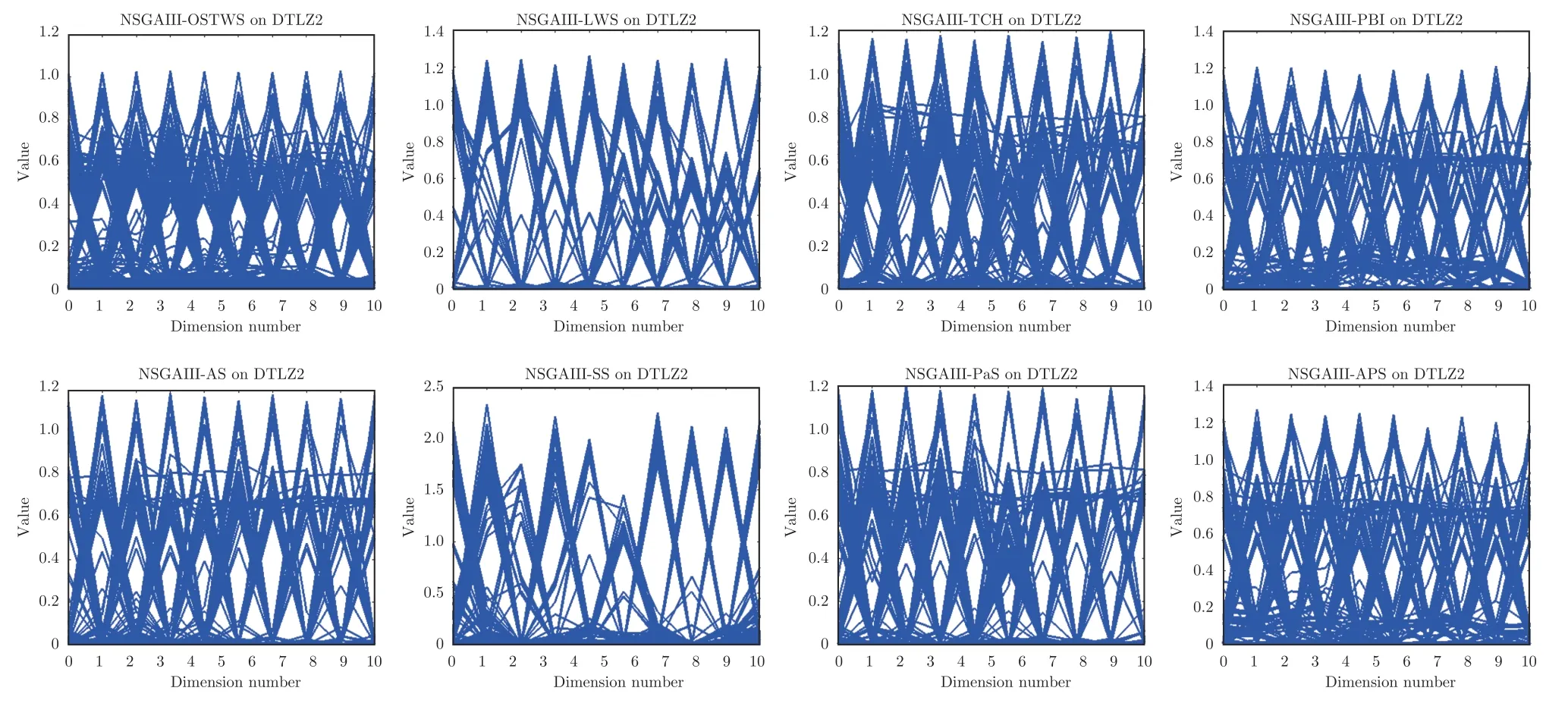
图5 NSGAIII-OSTWS,NSGAIII-LWS,NSGAIII-TCH,NSGAIII-PBI,NSGAIII-AS,NSGAIII-SS,NSGAIII-PaS 和NSGAIII-APS 在10 维DTLZ2 问题上所获得的解集Fig.5 Solution set of NSGAIII-OSTWS,NSGAIII-LWS,NSGAIII-TCH,NSGAIII-PBI,NSGAIII-AS,NSGAIII-SS,NSGAIII-PaS and NSGAIII-APS on DTLZ2 problem with 10-objectives

为进一步测试本文所提出的OSTWS 在多样性维持上的性能,我们在前沿面为线性(DTLZ1)、凹型(DTLZ2)、退化(DTLZ5)和不连续(DTLZ7)的问题上,将NSGAIII-OSTWS 与其他7 个算法进行对比.表6 展示了上述算法在最新多样性评价指标CPF 上的平均测试结果,可以看出OSTWS 在整体上取得了最佳的多样性性能.

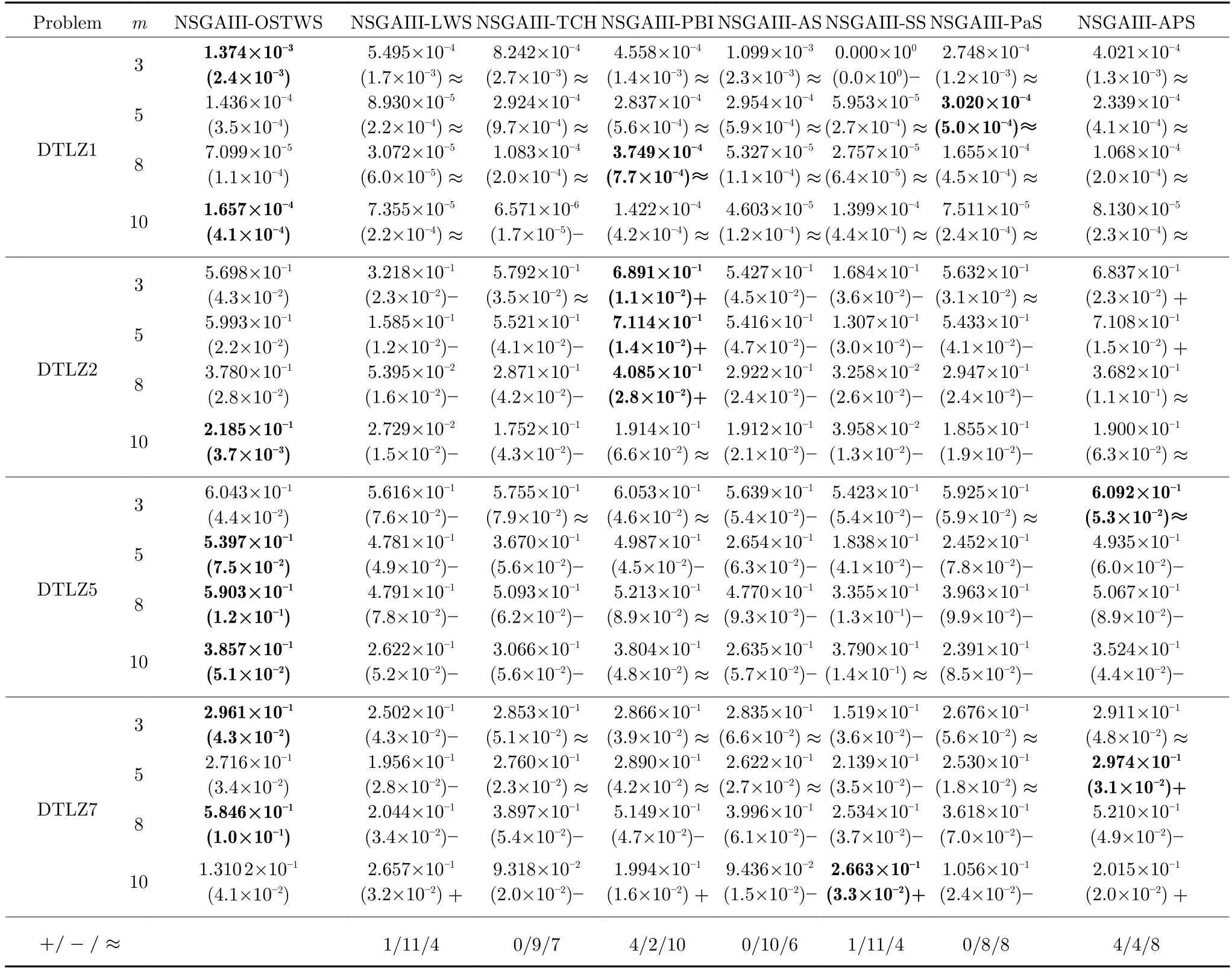
表6 OSTWS,LWS,TCH,PBI,AS,SS,PaS 和APS 方法在框架为NSGAIII,测试问题集为DTLZ1,DTLZ2,DTLZ5 和DTLZ7 上获得的CPF 值统计结果(均值和标准差).每个实例算法中的最好结果以加粗突出显示Table 6 The statistical results (mean and standard deviation) of the CPF values obtained by OSTWS,LWS,TCH,PBI,AS,SS,PaS and APS methods on the NSGAIII framework and DTLZ1,DTLZ2,DTLZ5 and DTLZ7 test problems.The best average value among the algorithms for each instance is highlighted in bold

为直观地展示算法在平衡收敛性和多样性上的综合性能,图4 给出了各个算法在IGD+上的性能打分图,分值越小表示该算法整体性能越好.从图4可以看出,算法NSGAIII-OSTWS 获得了最小的IGD+打分值,这表明与NSGAIII 的变体相比,NSGAIII-OSTWS 具有很强的综合性能.

2)算法整体性能验证与分析

为测试算法NSGAIII-OSTWS 的综合性能,将NSGAIII-OSTWS 与9 个先进的MaOEAs 进行对比实验,分别为NSGA-III[25]、Two_arch2[27]、SRA[29]、SPEAR[26]、DDEANS[33]、HpaEA[28]、ARMOEA[22]、MaOEA-IT[61]和PaRP/EA[62].表7、表8和表9 分别为上述算法在DTLZ、WFG 和LSMOP 测试问题集上所获得的IGD+统计结果.

表7 NSGAIII-OSTWS,NSGAIII,Two_arch2,SRA,SPEAR,DDEANS,HpaEA,ARMOEA,MaOEA-IT 和PaRP/EA在DTLZ1-7 上上获得的IGD+值的统计结果Table 7 The statistical results of the IGD+ values obtained by NSGAIII-OSTWS,NSGAIII,Two_arch2,SRA,SPEAR,DDEANS,hpaEA,ARMOEA,MaOEA-IT and PaRP/EA on DTLZ1-7

从表7,表8 和表9 的数据可以看出,与其它先进的MaOEAs 相比,NSGAIII-OSTWS 在绝大部分测试问题上取得了最佳IGD+值,这表明NSGAIIIOSTWS 在平衡收敛性和多样性上非常具有竞争力.首先,由表7,表8 和表9 可以看出,NSGAIIIOSTWS 的性能要明显优于经典算法NSGAIII,说明OSTWS 在很大程度上提高了NSGAIII 的整体性能,这再次验证了OSTWS 的有效性.其次,NSGAIII-OSTWS 的整体性能要强于其它最新算法Two_arch2、SRA、SPEAR、DDEANS、HpaEA、ARMOEA、MaOEA-IT 和PaRP/EA,尤其是在规则问题上,如DTLZ1-4 和WFG4-9.原因是NSGAIII-OSTWS 在规则问题上易于预估出PF 的形状,从而有利于加速种群的收敛.值得注意的是,DDEANS 也获得了较好的性能,原因是DDEANS采用了参考向量调整的方法,从而能在不规则测试问题上,如DTLZ7 和WFG1-2,较好地维持种群的多样性.

表8 NSGAIII-OSTWS,NSGAIII,Two_arch2,SRA,SPEAR,DDEANS,HpaEA,ARMOEA,MaOEA-IT 和PaRP/EA在WFG1-9 上上获得的IGD+值的统计结果Table 8 The statistical results of the IGD+ values obtained by NSGAIII-OSTWS,NSGAIII,Two_arch2,SRA,SPEAR,DDEANS,HpaEA,ARMOEA,MaOEA-IT and PaRP/EA on WFG1-9

表9 NSGAIII-OSTWS,NSGAIII,Two_arch2,SRA,SPEAR,DDEANS,HpaEA,ARMOEA,MaOEA-IT 和PaRP/EA在LSMOP1-9 上获得的IGD+值的统计结果Table 9 The statistical results of the IGD+ values obtained by NSGAIII-OSTWS,NSGAIII,Two_arch2,SRA,SPEAR,DDEANS,HpaEA,ARMOEA,MaOEA-IT and PaRP/EA on LSMOP1-9

为直观展示各个算法在平衡种群收敛性和多样性上的能力,图6 给出了所有算法在10 维DTLZ4问题上的最终种群分布图.从图6 可以看出,算法NSGAIII-OSTWS 获得的种群具有良好的收敛性和多样性,而对比算法NSGA-III、Two_arch2、SRA、SPEAR、DDEANS、HpaEA、ARMOEA 和MaOEA-IT 获得的种群都没有收敛到PF,这反映了NSGAIII-OSTWS 的优越性.此外,为进一步观察各个算法的收敛性能,图7 给出了各个算法在DTLZ、WFG 和LSMOP 测试问题上的平均GD表现分,分值越小表示该算法的收敛性性能越好.从图7 可以看出,算法NSGAIII-OSTWS 在绝大部分测试问题上都获得了最低的GD 表现分,表明与其它类型的算法相比,NSGAIII-OSTWS 具有很强的收敛能力,这归功于NSGAIII-OSTWS 算法采用的OSTWS 方法具有很高的搜索效率,从而使得种群能快速的收敛到PF.但对于退化和不连续的不规则测试问题DTLZ5-7,由于较难准确预估出真实PF 的形状,导致NSGAIII-OSTWS 在处理DTLZ5-7 问题时收敛性会有所下降.

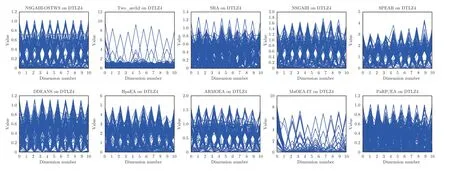
图6 SRA,SPEAR,DDEANS,HpaEA,ARMOEA,MaOEA-IT 和PaRP/EA 在10 维DTLZ4 问题上所获得的解集Fig.6 Solution set of NSGAIII-OSTWS,NSGAIII,Two_arch2,SRA,SPEAR,DDEANS HpaEA,ARMOEA,MaOEAIT and PaRP/EA on DTLZ4 problem with 10-objectives

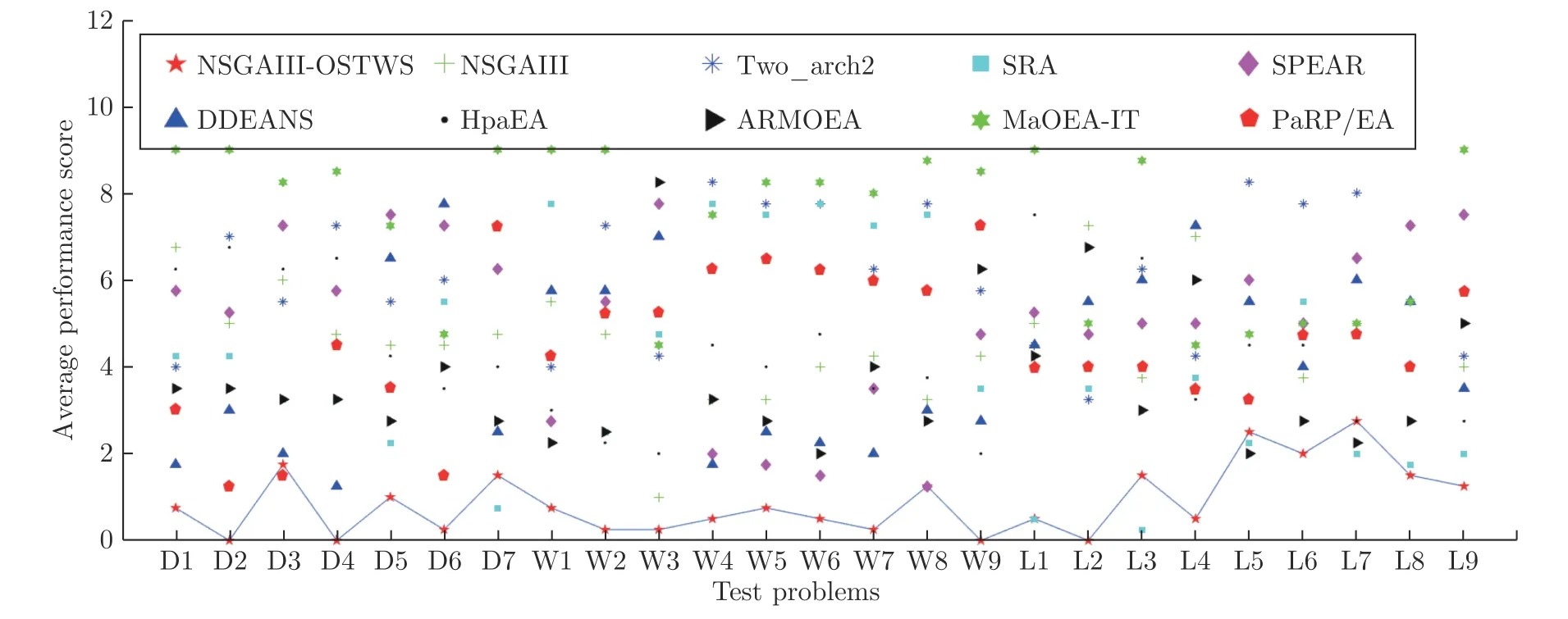
图7 NSGAIII-OSTWS,NSGAIII,Two_arch2,SRA,SPEAR,DDEANS,HpaEA,ARMOEA,MaOEA-IT 和PaRP/EA在所有测试问题,即DTLZ(Dx),WFG(Wx) 和LSMOP(Lx) 上的平均GD 表现分,分值越小,算法的整体性能越好.通过实线连接NSGAIII-OSTWS 的得分,以便易于评估分数Fig.7 Average performance score of NSGAIII-OSTWS,NSGAIII,Two_arch2,SRA,SPEAR,DDEANS,HpaEA,ARMOEA,MaOEA-IT and PaRP/EA on all test problems,namely DTLZ(Dx),WFG(Wx)and LSMOP(Lx).The smaller the score,the better the overall performance in terms of GD.The values of NSGAIII-OSTWS are connected by a solid line to easier assess the score

3)参数C的敏感性分析

NSGAIII-OSTWS 算法的核心是将各种问题的PF 转换为凸型曲面,其中参数C用于控制预设凸曲面的曲率,因此对算法的性能有着一定的影响.由于预设曲面为凸形,其曲率值C＞1.图8 为不同预设凸曲线在参考向量w上获得的最优解示意图.从中可以看出,当 1＜C ＜2 时,由参考向量w获得的最优解逐渐靠近w;当C=2 时,w获得的最优解正好位于w上;当C＞2 时,w获得的最优解逐渐远离w.由于参考向量主要用于对种群多样性的管理,最优解越靠近参考向量越有利于多样性的维护,因此C值取2 相比其它取值更能维持种群的多样性.为验证这一结论,本小节在凹凸混合问题WFG1、凹问题WFG4、线性问题DTLZ1 和不连续问题DTLZ7 上测试了C为{1.2,2,3,4,5,6,7,8,9,10}的IGD+性能.图9 为实验结果,可以看出,随着C值的增加,NSGAIII-OSTWS 的整体性能先逐渐提升后逐渐恶化,当C=2 时,算法具有最佳的性能,这验证了当C值取2 时算法具备良好性能这一结论.

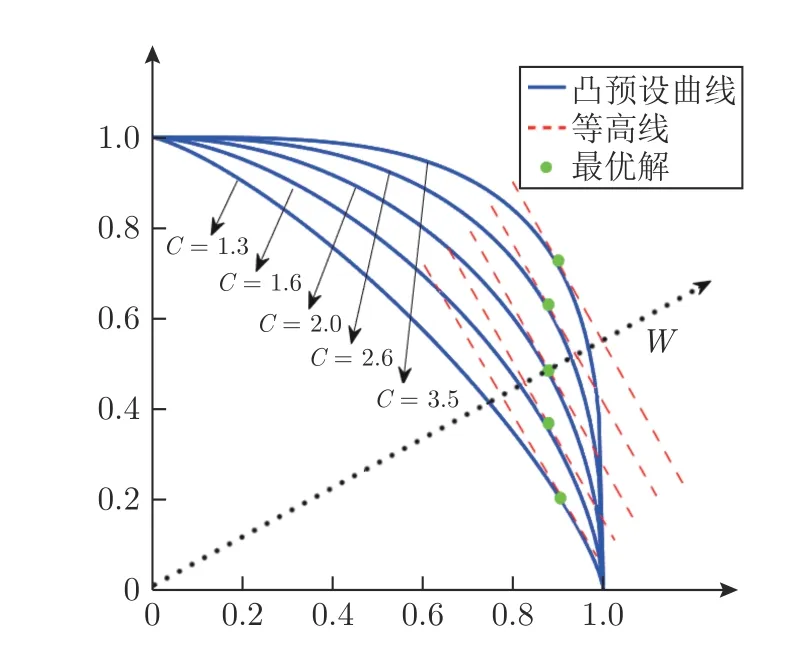
图8 不同预设凸曲线在参考向量w 上获得的最优解示意图Fig.8 The optimal solution obtained by different preset convex curves on the reference vector w

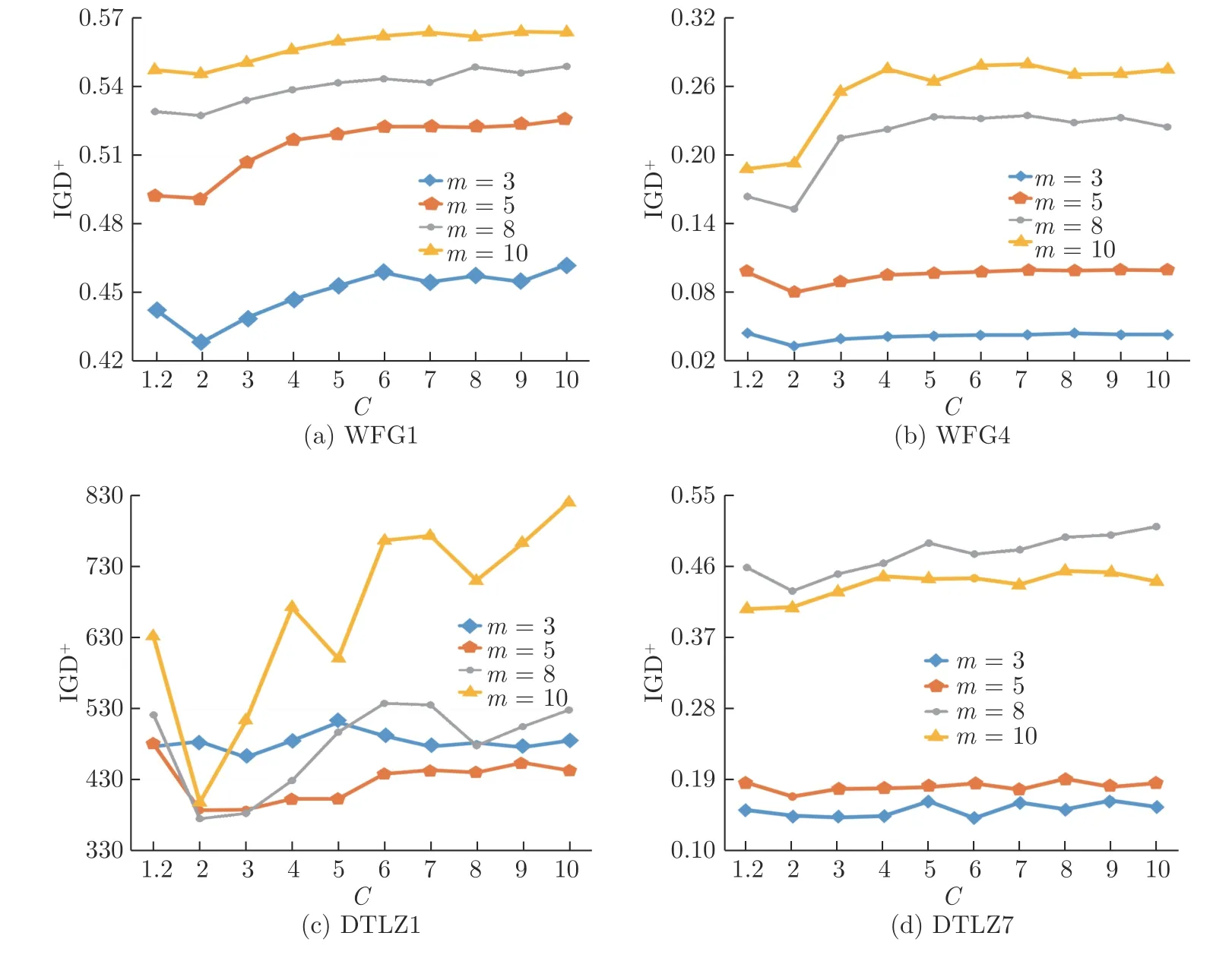
图9 不同 C 值在WFG1,WFG4,DTLZ1 和DTLZ7 问题的3,5,8 和10 目标维度上的IGD+均值Fig.9 The median IGD+ values of different C values on WFG1,WFG4,DTLZ1 and DTLZ7 problems with 3-,5-,8-,and 10-objectives

4 结论

为充分发挥权重求和搜索效率高的优势,同时又能处理好PF 形状为非凸的问题,本文提出了一种基于目标空间转换权重求和的超多目标进化算法,简称NSGAIII-OSTWS,其中目标空间转换权重求和方法(OSTWS)将各种问题的PF 转换为凸型曲面,再对其进行优化求解.为验证NSGAIIIOSTWS 的有效性,NSGAIII-OSTWS 与7 个NSGAIII 的变体以及9 个最新的MaOEAs 在WFG、DTLZ 和LSMOP 测试问题集上进行了实验对比.实验结果表明,相比其他算法,NSGAIII-OSTWS具备良好的竞争性能.

虽然所提算法NSGAIII-OSTWS 在处理MaOPs 上取得了优越的性能,但仍有一些开放性的工作值得进一步的探索.例如,不规则问题的PF 形状难以精确预估,这势必导致个体映射的不准确进而影响算法的性能.因此,未来需要进一步研究如何更加精确地映射个体.此外,将本文所提出的算法应用于现实生产和生活中各类实际问题的求解具有重要的价值,这也是未来需要进一步开展的工作.本文所提算法的源代码已在https://github.com/CIA-SZU/LTT 上公开.