分布式格林-安普特降雨径流模型研究
2022-05-28霍文博李致家杨明祥金双彦
霍文博,李致家,张 珂,杨明祥,金双彦,张 萍
(1.中国水利水电科学研究院,北京 100038; 2.黄河水利委员会水文局,河南 郑州 450004;3. 河海大学水文水资源学院,江苏 南京 210098)
流域水文模型的研究大约始于20世纪50年代[1]。作为对自然界中水文过程的模拟与概化,水文模型能够为流域水资源配置、洪水预报、水库调度等工作提供重要的参考和指导[2-4]。根据世界气象组织(WMO)的研究结果,在以蓄满产流为主的湿润地区,大部分水文模型表现较好[5-7];而在以超渗产流为主的半干旱及干旱地区,由于下垫面特征变化大、降雨时空分布不均、产流模式较为复杂等原因,水文模型模拟效果不佳[8-10],洪水预报难度较大[11-12]。为了提高半干旱地区的洪水预报精度,包为民等[13]提出了一种垂向混合产流模型,使用格林-安普特下渗方程计算流域中产生的超渗径流,用蓄满产流方程计算壤中流和地下径流,该模型在半干旱地区表现良好。李致家等[14-15]对新安江模型进行了改进,在新安江模型的基础上加入了超渗产流模块,用来计算流域中产生的超渗地面径流,研究表明,该模型在半干旱地区应用效果较好。
常见的超渗产流模型有霍顿(Horton)模型、霍尔坦(Holtan)模型、菲利普(Philip)模型、格林-安普特(Green-Ampt)模型等,其中格林-安普特模型[16]由于计算量小、计算精度高,被广泛用于下渗和超渗地面径流计算。为了提高格林-安普特模型在半干旱及干旱地区的应用效果,国内外许多学者对该模型进行了研究和改进[17-21]。
传统概念性水文模型在计算时往往将流域看作一个整体,或者将一个流域划分为多个子流域,每个子流域内的降雨及模型参数相同。在半干旱及干旱地区,由于下垫面特征变化较大、降雨时空分布不均,传统概念性水文模型很难准确反映流域内的降雨及下垫面变化情况。随着计算机计算速度的提升以及卫星遥感等技术的发展,水文模型逐渐朝着更加精细化的方向发展,基于物理基础的分布式水文模型越来越多地受到关注。分布式水文模型将流域划分为细小的网格,在每个网格中单独计算蒸散发及产汇流过程,能够更精确地考虑流域内降雨和下垫面变化的特点。本文构建一种基于网格计算的分布式格林-安普特降雨径流模型,并应用于陕北黄土高原地区两个半干旱流域,以研究该模型的应用效果。
1 模 型 构 建
分布式格林-安普特降雨径流模型主要由蒸散发模块、产流模块和汇流模块三部分构成(图1),三部分计算均在以DEM数据为基础的正交网格内进行。在每个网格中,输入模型的降雨数据首先进入蒸散发模块,由该模块计算网格内的蒸散发量,然后通过产流模块计算网格内的下渗量及径流量,最后根据网格之间的汇流演算次序,通过坡面汇流和河道汇流的计算,得到流域出口断面及其他各断面的流量过程。

图1 分布式格林-安普特降雨径流模型结构Fig.1 Module and structure of distributed Green-Ampt rainfall-runoff model
1.1 蒸散发模块
在蒸散发模块中,使用新安江模型中的三层蒸散发模型[1]进行网格内的蒸散发和净雨量计算,将每个网格内的土壤分为上层、下层和深层,各层土壤蒸散发量分别为
Eu=kEM
(1)
El=(kEM-Eu)Wl/WLM
(2)
Ed=C(kEM-Eu)-El
(3)
式中:Eu为上层土壤蒸散发量,mm;El为下层土壤蒸散发量,mm;Ed为深层土壤蒸散发量,mm;k为蒸散发折算系数;EM为实测水面蒸发量,mm;Wl为实际土壤含水量,mm;WLM为下层张力水蓄水容量,mm;C为深层蒸散发系数。总蒸发量E为
E=Eu+El+Ed
(4)
1.2 产流模块
采用格林-安普特下渗公式计算每个网格内土壤的下渗能力,下渗方程为
(5)
其中Δθ=θS-θI
式中:f(t)为土壤下渗能力,mm/h;K为饱和水力传导度,mm/h;ψ为湿润锋处的土壤吸力,mm;Δθ为土壤饱和含水率与初始含水率之差;F(t)为累积下渗量,mm;t为时间,h;θS为土壤饱和含水率;θI为土壤初始含水率。
按照美国农业部(USDA)土壤分类标准,Rawls等[22]通过试验得出了不同土壤类型的4个参数值:土壤总孔隙度θt、土壤有效孔隙度θe、ψ和K。将土壤参数值代入格林-安普特下渗方程即可计算出每个网格内的超渗径流量,具体步骤如下。
a.由式(5)计算网格内f(t),其中K、ψ和θS的值可根据土壤类型得到(θS=θe)。θI的初值由日模型率定得到,在次洪模型计算中,各时段θI等于上一时段土壤含水率的计算结果。
b.根据f(t)和净雨量p,计算网格内径流量Q:

(6)
c.网格中土壤在一个时段内的下渗量i为
i=p-r
(7)
第τ个时段网格内累积下渗量为
F(τ)=i1+i2+…+iτ
(8)
式中iτ为第τ个时段的下渗量。
将F(t)带入式(5),计算下个时段网格中的f(t)。每个网格存在一个最大累积下渗量Fm,其值与土层厚度有关。当土F(t)>Fm时,多出的水量形成地下径流。
d.重复步骤a至c,依次计算每个网格各时段的径流量Q。
1.3 汇流模块
在汇流模块中使用一维扩散波方程组计算流域坡面汇流过程[23]:
(9)
式中:hs为坡面水流水深,m;us为坡面水流平均流速,m/s;qs为单位时间内坡面径流深,m/s;Soh为沿出流方向的地表坡度;Sfh为沿出流方向的地表摩阻比降;x为流径长度,m。在计算网格间坡面汇流时,需要将式(9)在每个网格单元上进行离散,其中连续性方程为
(10)
式中:Agc为网格单元面积,m2;Qs为网格单元内径流量,m3/s;Qsout为网格单元出流量,m3/s;Qsup为上游网格入流量,m3/s。
河道汇流使用基于网格的马斯京根汇流演算法[24]计算,有关坡面汇流与河道汇流的详细计算过程见文献[23-24]。
2 应 用 实 例
2.1 研究流域
选择陕西省曹坪流域和志丹流域(图2)为研究流域,两流域均属于半干旱地区。曹坪水文站位于黄河无定河水系的二级支流岔巴沟,控制流域面积187 km2。该流域地貌主要为黄土丘陵沟谷,气候干旱,植被覆盖率较低。流域年均降水量443 mm,流域内共有12个雨量站和1个水文站。志丹水文站是黄河流域北洛河水系周河的控制站,控制流域面积774 km2,流域多年平均降水量509.8 mm,流域内植被覆盖差,水土流失较为严重,共有6个雨量站和1个水文站。
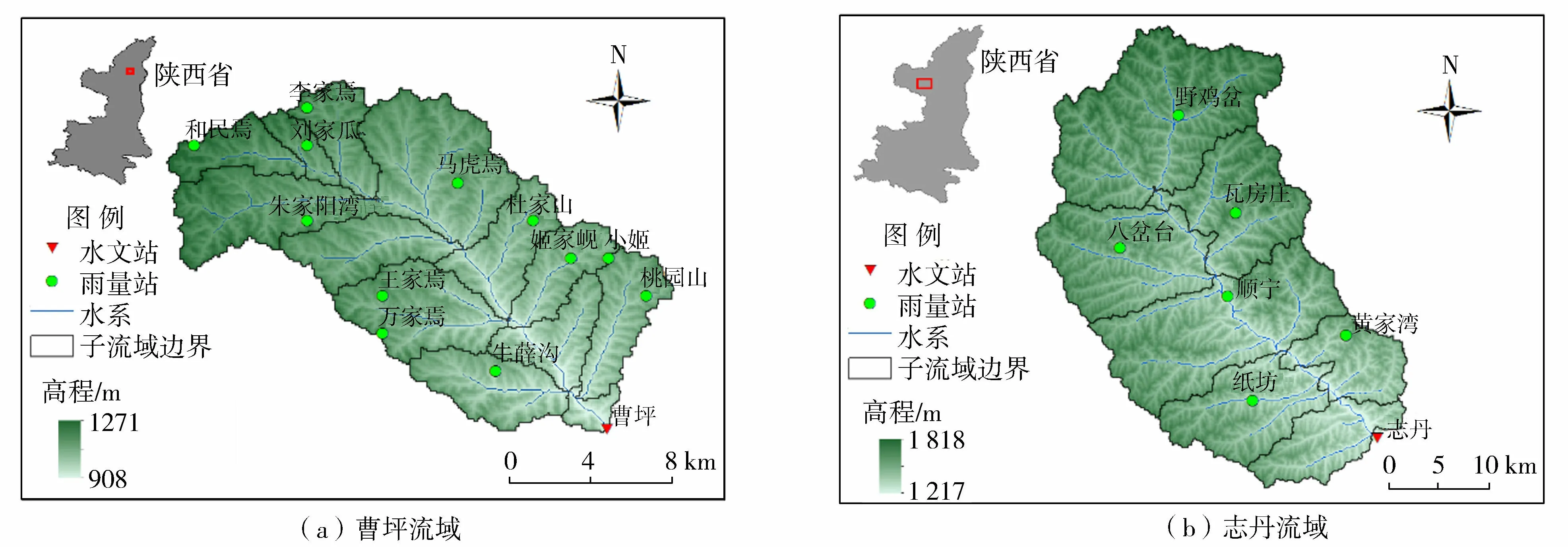
图2 流域地理位置Fig.2 Location of the studying basins
表1为曹坪流域和志丹流域的土壤类型及各类土壤参数,图3为两流域土壤类型分布。本文使用的土壤数据为美国农业部(USDA)提供的1 km×1 km数据(https://www.usda.gov/)。
图3 流域土壤类型分布Fig.3 Distribution of soil types in the studying basins

表1 流域土壤类型及参数
2.2 模型选择与参数率定
分别选择格林-安普特模型和基于物理基础下渗能力分布曲线的格林-安普特模型(GA-PIC模型)与本文提出的分布式格林-安普特降雨径流模型进行对比,比较3个模型在两个半干旱地区的应用效果。格林-安普特模型利用一条经验下渗能力分布曲线来反映流域下垫面分布不均的特点;GA-PIC模型[20]是将格林-安普特模型中的经验下渗能力分布曲线改进为具有物理基础的下渗能力分布曲线,可以更准确地反映半干旱地区降雨及下垫面特征的时空变化情况,在半干旱地区应用效果较好[20-21]。以上两个模型都是以子流域为单元计算产汇流过程,而本文提出的分布式格林-安普特降雨径流模型是以正交网格为基本单元进行产汇流计算。
在3个模型中,GA-PIC模型和分布式格林-安普特降雨径流模型中的3个参数K、θS和ψ是根据土壤性质得出(表1)的,其余参数均使用人工优选法和SCE-UA自动优选法[25-26]结合率定得到:不敏感参数使用人工优选法,敏感参数使用SCE-UA自动优选法,这样可以减少异参同效现象的发生,提高参数精度。各模型分别进行日模拟和时段模拟,日模拟计算时间步长为24 h,模拟结果为时段模拟提供初始土壤含水量等下垫面状态初值。由于曹坪流域面积较小(187 km2),流域汇流时间短,洪水起涨快,时段模拟计算时间步长选择10 min;志丹流域面积相对较大(774 km2),流域汇流时间比曹坪流域长,时段模拟计算时间步长选择1 h。
2.3 模型应用对比
分布式格林-安普特降雨径流模型中网格单元大小为1 km×1 km。选择径流深相对误差、洪峰相对误差、峰现时间误差和确定性系数4 个指标来评价模型的模拟精度。
2.3.1 曹坪流域
2.3.1.1 总体模拟结果
在曹坪流域选择2000—2010年共17场洪水,其中2000—2006年的10场洪水用来率定模型参数,2006—2010年的7场洪水用于验证模型,各模型模拟结果见表2,表中径流深相对误差、洪峰相对误差和峰现时间误差值为各场洪水的绝对平均值,确定性系数为各场洪水的平均值。

表2 曹坪流域各模型模拟结果
通过表2可以看出:①在径流深模拟方面,率定期GA-PIC模型模拟结果相对误差最小,为23.2%,分布式格林-安普特降雨径流模型次之,相对误差为26.1%;验证期分布式格林-安普特降雨径流模型模拟结果相对误差最小,为38.2%。②在洪峰模拟方面,分布式格林-安普特降雨径流模型在3个模型中表现最佳,其率定期和验证期洪峰相对误差均明显低于另外两个模型。③对于峰现时间的模拟,分布式格林-安普特降雨径流模型同样优于另外两个模型。峰现时间的模拟精度主要取决于模型汇流模块,以上模拟结果说明,分布式格林-安普特降雨径流模型中基于网格的坡面汇流与河道汇流模块能够更准确地计算径流汇集到流域出口断面的时间。④在确定性系数方面,率定期GA-PIC模型和分布式格林-安普特降雨径流模型均为0.17,高于格林-安普特模型的确定性系数0.04;验证期分布式格林-安普特降雨径流模型确定性系数为0.56,在3个模型中最高。3个模型验证期确定性系数均高于率定期的值,通过观察各场洪水的模拟过程线发现,这主要是由于验证期各模型对于峰现时间的模拟更准确,因此模拟过程线与实测洪水过程线拟合得更好,确定性系数更高。在半干旱地区,由于洪水过程陡涨陡落,洪水过程线形状尖瘦,当峰现时间误差稍大时确定性系数会变得很低,此时确定性系数并不能准确反映模型模拟结果的好坏。在半干旱中小流域,评价模型结果的准确性影响因素主要为洪峰相对误差和峰现时间误差这两个指标。
总体来看,在率定期分布式格林-安普特降雨径流模型与GA-PIC模型表现比较接近,好于格林-安普特模型。验证期分布式格林-安普特降雨径流模型表现好于另外两个模型,尤其对于洪峰的模拟误差更小。曹坪流域属于山区中小流域,在该地区洪峰预报比洪量预报更为重要,因此分布式格林-安普特降雨径流模型在曹坪流域的总体模拟结果为3个模型中最佳。
2.3.1.2 具体场次洪水模拟结果分析
分析3个模型对于各场洪水的模拟过程线,可以更明显地看出分布式格林-安普特降雨径流模型的特点和优势。图4(a)为各模型对验证期2010050415号洪水模拟的结果对比。该场洪水实测总雨量7.4 mm,实测洪峰流量20.8 m3/s,实测径流深0.60 mm,降水量、径流量和洪峰流量都非常小。格林-安普特模型模拟的洪峰流量和径流深分别为2.0 m3/s和0.07 mm,洪峰相对误差为-90.4%,径流深相对误差为 -88.3%;GA-PIC模型模拟的洪峰流量和径流深分别为2.2 m3/s和0.08 mm,洪峰相对误差为 -89.4%,径流深相对误差为 -86.7%,模拟结果与格林-安普特模型模拟结果比较接近。对于这场由小降水量引起的洪量较小的洪水,格林-安普特模型和GA-PIC模型对径流量及洪峰的模拟误差很大。分布式格林-安普特降雨径流模型模拟的洪峰流量和径流深分别为19.0 m3/s和0.59 mm,洪峰相对误差为 -8.7%,径流深相对误差为 -1.7%,模拟精度明显高于另外两个模型。对于其他降水量较小,产流量较低的洪水,分布式格林-安普特降雨径流模型模拟结果也总体好于另外两个模型,这是因为当降水量和雨强较小时,流域中只有少部分土壤湿度大、土层较薄、下渗能力小的区域产生了径流,分布式格林-安普特降雨径流模型是在每个网格上单独计算产流的,各网格产流与否、产流量大小都相互独立,因此分布式格林-安普特降雨径流模型能够较精确地计算出流域任何一个位置的产流过程。而格林-安普特模型和GA-PIC模型是利用下渗能力分布曲线在整个流域面积上计算产流,对于个别区域产生的少量径流模拟不够精确。在降水量和径流量均较小的洪水中,分布式格林-安普特降雨径流模型可以比格林-安普特模型和GA-PIC模型更准确地模拟出产流面积的分布和产流量的大小。
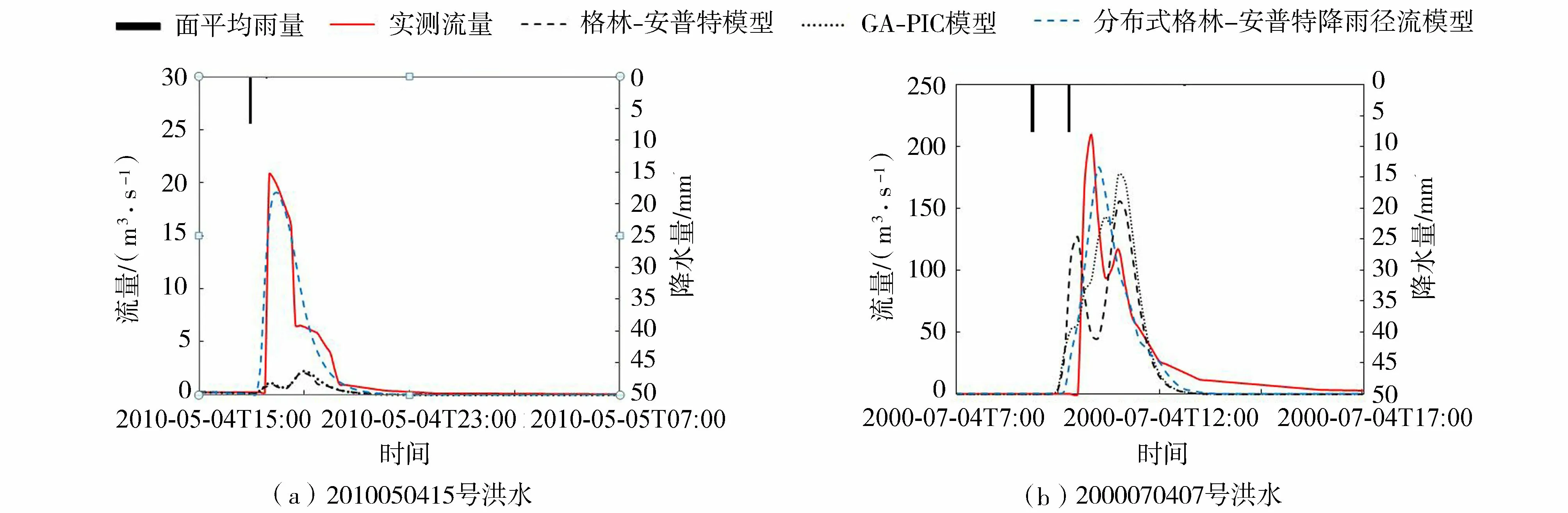
图4 曹坪流域3个模型模拟结果对比Fig.4 Result comparison of three models for the Caoping Basin
另外,2010050415号洪水过程只有一个洪峰,而格林-安普特模型和GA-PIC模型模拟出现了两个洪峰,峰现时间误差均为80 min,说明两个模型对于该场洪水汇流时间的模拟误差较大,各子流域洪峰汇集到总流域出口的模拟时间与实际时间不符,因此出现两个洪峰。分布式格林-安普特降雨径流模型对这场洪水模拟的峰现时间误差为20 min,模拟洪峰形状与实际洪峰形状非常接近,并且只有一个洪峰。说明在分布式格林-安普特降雨径流模型中,基于网格的坡面汇流和河道汇流计算模块更准确地模拟了流域中不同位置的产流汇集到流域出口的过程。
图4(b)为3个模型对2000070407号洪水模拟结果对比。该场洪水实测洪峰流量209.6 m3/s,实测径流深4.60 mm,是曹坪流域2000—2010年中洪峰流量较大的一场洪水。格林-安普特模型模拟的洪峰流量和径流深分别为154.7 m3/s和4.03 mm,洪峰相对误差为 -26.2%,径流深相对误差为 -12.4%,峰现时间误差为40 min;GA-PIC模型模拟的洪峰流量和径流深分别为177.2 m3/s和4.64 mm,洪峰相对误差为 -15.5%,径流深相对误差为0.9%,峰现时间误差为40 min,总体模拟精度高于格林-安普特模型;分布式格林-安普特降雨径流模型模拟的洪峰流量和径流深分别为182.7 m3/s和4.55 mm,洪峰相对误差为-12.8%,径流深相对误差为 -1.1%,峰现时间误差为10 min。在这场洪水中,分布式格林-安普特降雨径流模型对洪峰流量和径流深的模拟精度与GA-PIC模型模拟精度相近,而峰现时间误差明显低于GA-PIC模型和格林-安普特模型,说明分布式格林-安普特降雨径流模型中基于网格的汇流计算模块对流域汇流过程的模拟更加准确。
2.3.2 志丹流域
选择志丹流域2000—2010年共13场洪水,其中前8场洪水用来率定模型参数,后5场洪水用于验证模型,各模型模拟结果见表3。
在径流深模拟方面,率定期GA-PIC模型模拟结果相对误差最小,为35.7%,分布式格林-安普特降雨径流模型模拟相对误差为36.2%,稍高于GA-PIC模型;验证期GA-PIC模型模拟结果相对误差最小,为47.4%,分布式格林-安普特降雨径流模型次之,相对误差为48.6%。在洪峰模拟方面,分布式格林-安普特降雨径流模型在3个模型中表现最佳,其率定期洪峰相对误差为38.3%,验证期洪峰相对误差为42.0%,均低于另外两个模型。对于峰现时间的模拟,分布式格林-安普特降雨径流模型同样优于另外两个模型,其率定期和验证期的峰现时间误差分别为0.7 h和0.9 h,也说明分布式格林-安普特降雨径流模型中基于网格的坡面汇流与河道汇流模块对流域汇流的计算和模拟更准确。分布式格林-安普特降雨径流模型在率定期和验证期模拟结果的确定性系数分别为0.51和0.23,均高于另外两个模型。
总体来看,在志丹流域分布式格林-安普特降雨径流模型与GA-PIC模型表现比较接近,好于格林-安普特模型。分布式格林-安普特降雨径流模型对于径流深的模拟精度低于GA-PIC模型,而对洪峰的模拟精度高于GA-PIC模型。
2.3.3 对比分析
对比3个模型在志丹流域和曹坪流域的模拟结果可以发现,曹坪流域各模型模拟精度普遍高于志丹流域,这主要是由降雨观测资料精度导致的。志丹流域面积774 km2,流域内共有7个雨量观测站,站网密度为110.6 km2/站;曹坪流域面积187 km2,流域内共有13个雨量观测站,站网密度为14.4 km2/站,密度明显高于志丹流域,可以更好地记录降雨空间变化特征。同时,曹坪流域雨量观测站观测资料的时间间隔比志丹流域更小,对于降雨强度的观测精度更高,因此各模型在曹坪流域模拟精度高于志丹流域。
3 结 语
本文构建了一种基于网格计算流域蒸散发及产汇流的分布式格林-安普特降雨径流模型,并应用于陕北黄土高原地区两个半干旱流域,研究结果表明,分布式格林-安普特降雨径流模型在半干旱地区的模拟精度总体高于GA-PIC模型和格林-安普特模型,尤其对于洪峰的模拟精度明显高于另外两个模型。分布式格林-安普特降雨径流模型模拟的洪峰相对误差和峰现时间误差更小,说明其对产流和汇流的模拟精度更高,模型中基于网格的坡面汇流与河道汇流模块能够更准确地计算径流汇集到流域出口断面的时间。同时,与另外两个模型相比,分布式格林-安普特降雨径流模型能够更精确地计算流域不同位置的产流过程,更准确地模拟流域产流面积分布情况。
半干旱地区降雨时空分布不均,超渗产流主要受降雨强度的影响,因此降雨观测精度对径流预报精度影响较大,要提高半干旱地区洪水预报精度从根本上需要提高降雨观测和预报精度。半干旱地区洪水预报一直都是水文预报研究的重点和难点,分布式格林-安普特降雨径流模型可以为提高半干旱地区洪水预报精度提供参考。
