基于排队论的工程装备战场抢修力量配置策略研究

陈 威 鲁冬林 沈溥淏 胡嘉旭,3 郭 聪

（1.陆军工程大学，南京 210000；2.94679部队，南京 210000；3.95979部队，泰安 271000）

工程装备在执行各类工程保障任务时，特别是在现代战争中，由于作战环境复杂、各种高新武器层出不穷，更加容易受到各种损伤，严重影响工程保障任务的效率。因此，需要对受损的工程装备及时进行战场抢修。在战场抢修中，必须充分考虑工程装备的战场抢修力量的配置策略，将有限的抢修力量合理配置，提升战时装备维修效率[1]。

战场抢修力量配置策略是在战场抢修力量有限的情况下，通过合理安排战场抢修力量，制定战场抢修规则，充分发挥战场抢修力量，以提供最满意的维修服务效率，达到最大的战场抢修效能。战场抢修力量配置的方法可归纳为集中配置和分散配置两种。为了进一步分析战场抢修力量配置策略问题，用排队论中的有关理论建立其数学模型，并通过相关的基本数量指标的计算和分析来确定其战场抢修力量配置策略的优劣。

1 排队论模型一般形式及衡量指标

排队是日常生活中随处可见的现象，如在超市、汽车站等地点都能看到此类现象。排队现象的出现，是由于顾客的数量超过了服务系统的容量，顾客无法立即得到服务[2]。同理，在战时，如果需要进行抢修的工程装备超过了相关维修部门的容量，那么抵达的受损工程装备不能够立刻得到维修，就会出现战损工程装备在维修部门等待维修的排队现象。此时，可以将战损工程装备与抢修部门看成一个排队系统，排队过程如图1所示[3]。

图1 受损工程装备等待维修时的排队模型

排队论（Queuing Theory）又称随机服务系统理论，是通过对服务对象到来及服务时间的统计研究，得出这些数量指标（等待时间、排队长度、忙期长短等）的统计规律，然后根据这些规律改进服务系统的结构或重新组织被服务对象，使得服务系统既能满足服务对象的需要，又能使机构的费用最经济或某些指标最优[4]。

排队模型通常可以用X/Y/Z/A/B/C表示。其中：X表示顾客相继到达的间隔时间的分布；Y表示服务时间的分布；Z表示服务台个数；A表示系统容量限制（默认为∞）；B表示顾客源数目（默认为∞）；C表示服务规则（默认为先到先服务）。

可以用以下指标对排队系统进行衡量：（1）服务队长Ls，正在接受服务的顾客数；（2）排队长Lq，在队列中等待的顾客数；（3）逗留时间Ws，顾客在服务中消耗的时间；（4）等待时间Wq，顾客在队列中等待的时间。

2 建立排队论模型

2.1 集中配置时

设某作战分队用的装备数量为m，损坏的装备按泊松分布，到达维修点进行维修，其需维修的数量不限，先到先维修。已知装备的平均故障率即待修理装备的平均到达率为λ，装备平均修复率为μ，且λ＜μ，系统的服务强度ρ=λ/cμ。现有c个装备维修小组，可同时维修若干台装备。若c个装备维修小组集中在一个服务点上，可用图2表示集中配置时战损工程装备的排队模型。此时排队模型符合排队系统的标准M/M/c/∞/∞模型，可用下列公式计算相关数量指标[5]。

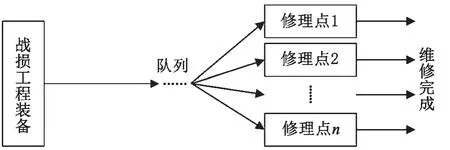
图2 集中配置时的排队模型

（1）维修组空闲的概率为：

（2）装备到达维修点必须等待服务的概率为：

（3）装备等待修理的平均台数为：

（4）维修组正在修理中的装备的平均台数为：

（5）平均等待修理时间为：

（6）平均修理时间为：

2.2 分散配置时

若上述的c个装备维修小组分散配置在各个不同的服务点上，可用图3表示分散配置时战损工程装备的排队模型。此时排队模型则符合排队系统的标准M/M/1/∞/∞模型，平均服务强度ρ=λ/μ，可用下列公式计算相关数量指标。

（1）维修组空闲的概率为：

（2）装备到达维修点必须等待服务的概率为：

（3）装备等待修理的平均台数为：

（4）维修组正在修理中的装备的平均台数为：

图3 分散配置时的排队模型

（5）平均等待修理时间为：

（6）平均修理时间为：

3 应用分析

高寒山地边境反击作战中，工程兵部（分）队围绕几个主要作战通道遂行工程保障任务。由于高寒山地地区地形复杂、气候寒冷以及装备工作环境恶劣等，工程装备损坏率急剧增加，而修理人员、修理保障装备及维修器材有限，基层级修理分队一般采用定点维修保障的方法对所属的工程装备进行维修保障。以军用工程机械为例，设损坏的军用工程机械按泊松分布到达定点维修点进行维修，损坏的军用工程机械平均到达率λ为每小时0.9台，每个维修组的维修能力μ为每小时0.4台。若集中配置，可同时维修3台军用工程机械；若分散配置，分3个独立修理点，每个维修点只能同时维修1台军用工程机械，且损坏的军用工程机械平均到达率相同。

从条件可以看出，当集中配置时，战损工程装备的排队模型符合M/M/3/∞/∞模型；当分散配置时，在3个定点维修站，每个维修点的排队模型都符合M/M/1/∞/∞模型。根据集中配置和分散配置的排队论相关公式，可分别求出两种排队模型的基本数量指标，结果见表1。

从计算结果可以看出，维修组集中配置的情况下，维修组空闲的概率P0、装备必须等待服务的概率Pn、装备等待修理的平均台数Lq、修理中的装备的平均台数Ls、平均等待修理时间Wq以及平均修理时间Ws等指标均比分散配置的情况小。这表明该情形下维修组集中配置比分散配置时具有更高的维修效率，分散配置时，维修组空闲的概率P0为25%，远高于集中配置时的7.5%，维修效率却比集中配置时低，说明该情形下分散配置时各维修组忙闲不均，不利于提高维修效率，因此最优选择是将维修小组集中配置。

若要求装备等待修理的平均台数Lq不大于0.15且平均等待修理时间Wq不大于0.1 h，此时该维修分队无法满足修理要求，需要由上级向下加强维修力量。若在维修组集中配置的情形下，当维修组总数c分别为3、4、5、6、7时，利用排队论建立模型，经过公式计算，可得表2。

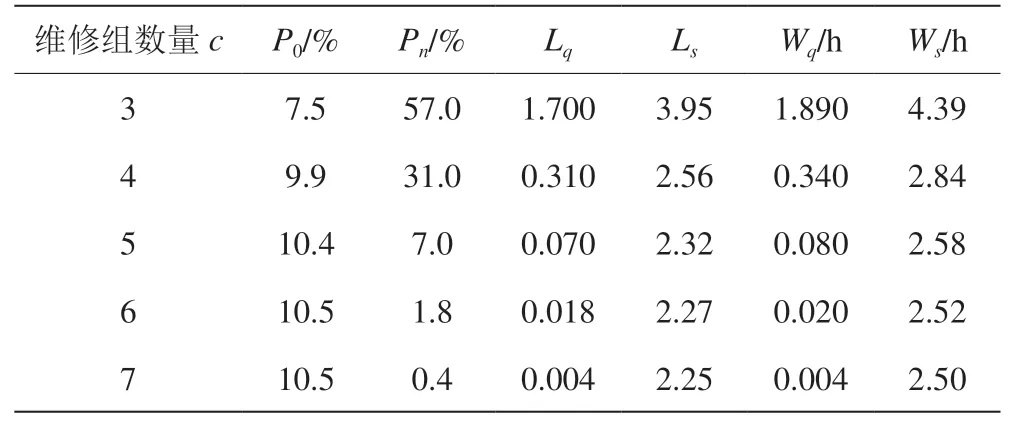
表2 不同数量维修组的参数指标

从计算结果可以看出：当维修组数量增加时，各项数据指标有较大提升；当维修组数量c达到5个时，满足上述约束条件。故在这种约束下，需要由上级向下至少增加2个维修组才能满足修理需求。

4 结语

为了实现工程装备抢修力量的科学配置，提高装备抢修效率，利用排队论分别建立了工程装备战场抢修力量在不同配置策略的数学模型，通过分别计算工程装备抢修力量在集中配置和分散配置时的相关参数指标，以此选择最优的工程装备战场抢修配置策略，为指挥员在工程装备战场抢修决策提供科学依据。