基于深度强化学习的多小区NOMA 能效优化功率分配算法

胡浪涛，毕松姣，刘全金，吴建岚，杨 瑞

(安庆师范大学电子工程与智能制造学院 安徽 安庆 246133)

近年来，随着移动用户数量的爆炸式增长，多小区间的功率分配问题引起了广泛关注。此外，小区内和小区间的干扰管理对于提高蜂窝网络系统的能量效率也很重要。为了解决移动用户密度大的问题，非正交多址接入技术成为当前通信系统的研究热点之一[1-5]。

非正交多址接入(non-orthogonal multiple access，NOMA)技术的基本思想是在发送端采用非正交方式发送信号，在接收端采用串行干扰删除技术，从而实现信号的正确解调。已有很多文献研究了NOMA 系统的功率分配问题。文献[1]提出一种单输入单输出情况下的优化问题，随后将单输入单输出解决方案扩展为多输入多输出场景，在满足每个用户的最小速率要求的服务质量和总功率约束条件下使总容量最大化。文献[2]将深度强化学习(deep reinforce learning, DRL)应用于无授权NOMA系统的决策中，旨在减轻冲突并提高未知网络环境中的系统吞吐量。文献[3]研究了包含任意用户的单个NOMA 簇，目标是在满足每个用户所需的最小数据速率下最大化能量效率。文献[4]研究了集群中多用户多输入多输出NOMA 系统中最大化能量效率的功率分配方案。

很多功率优化函数是非凸的，且优化问题是非确定性多项式(non-deterministic polynomial, NP)难题，机器学习技术被引入用于解决功率优化问题。机器学习包括监督学习、非监督学习和强化学习等。监督学习需要训练样本带有类别标签，通过训练深度神经网络逼近已给出的标签，文献[6-7]给出了关于监督学习的实现方案。无监督学习的训练样本没有标签，文献[8-9]相继提出了多种无监督学习研究方案。强化学习讨论一个智能体如何在未知环境里面最大化能获得的奖励。因为监督学习需要提前给出类别标签，非监督学习在学习过程中无反馈，强化学习在近年来成为无线通信中功率分配的热门技术[10-14]。文献[10]将Actor-critic 算法应用于NOMA 系统中不同认知无线电之间的功率分配，其目的是满足认知无线电最小数据速率要求的同时，最大化系统能量效率。文献[11]研究使用深度Q 网络(deep Q networks, DQN)算法，旨在最大化整个网络的能量效率。文献[12]考虑动态无线网络中发射功率和信道的联合决策优化问题，通过构造DQN 解决状态空间过大的复杂决策问题，提高系统能量效率。文献[13]提出基于Actor-Critic算法研究混合能源异构网络中用户调度和资源分配的最优策略，目的是最大化系统的能量效率。

本文针对单输入单输出的下行多小区NOMA系统，研究了一种DRL 的功率分配算法(energy efficient power allocation-DQN，EEPA-DQN)，将DQN 作为动作−状态值函数，目的是优化信道功率分配，使系统能量效率最大化。将基站到用户的单个信道视为一个智能体，使用经验回放池将数据进行集中训练，分步执行时使用该智能体学习到的策略。仿真结果表明，EEPA-DQN 算法与加权最小均 方 误 差 (weight minimum mean square error,WMMSE)[15]、分 式 规 划(fractional programming,FP)[16]、最大功率(maximal power, MP)[17]和随机功率 (random power, RP)[18]等算法相比，得到的能量效率更高，收敛速度更快。

1 下行多小区NOMA 系统模型

基站向不同用户发送消息，每个基站发送给用户的叠加信号表示为：

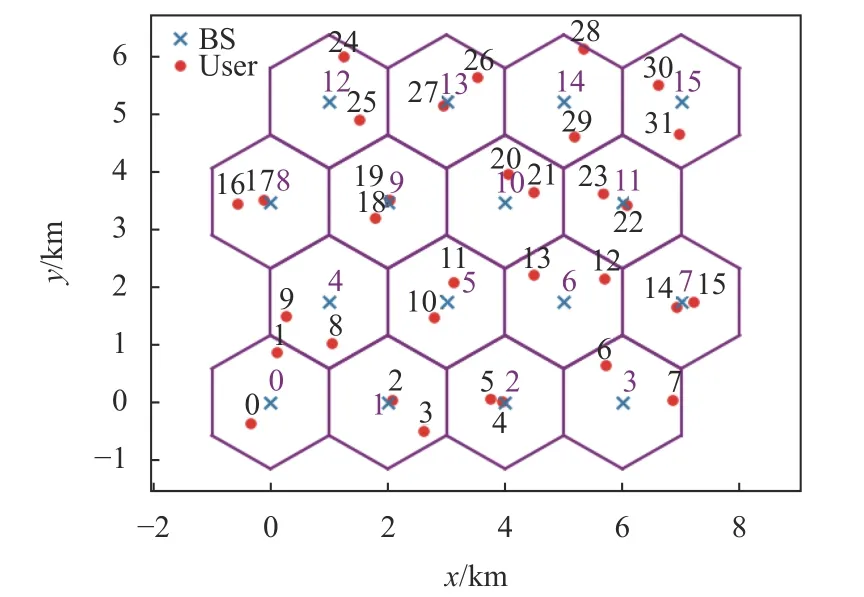
图1 蜂窝网络模型

2 EEPA-DQN 算法设计

2.1 深度Q 网络简介

强化学习算法讨论一个智能体如何在一个复杂不确定的环境里获得最大化的奖励。本文采用深度强化学习DQN 算法，基于离散时间马尔可夫决策过程(Markov decision process, MDP)，在有限的动作和状态空间中最大化获得的奖励。在时隙t，从环境中获取状态st∈S， 智能体选择动作at∈A，并与环境交互，获得奖励rt∈R并转换到下一个状态st+1，其中 ，A是动作集合，S是状态集合，P是当前状态转移到下一个状态的状态转移概率，R是奖励集合。强化学习框图如图2 所示。

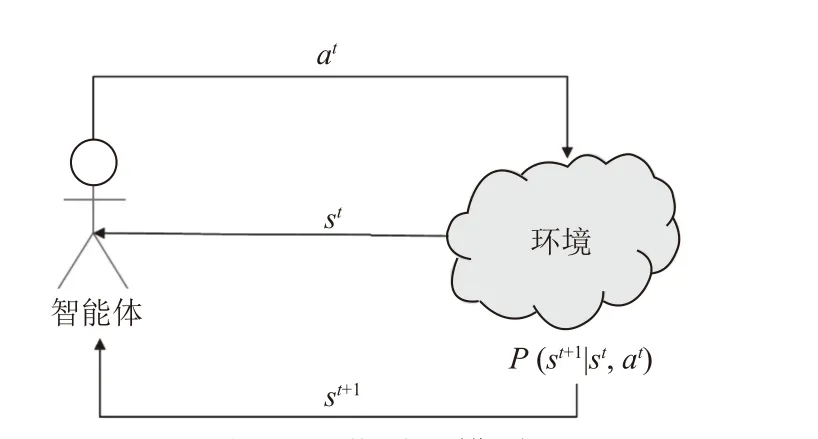
图2 强化学习模型

由于状态可以是连续的，DQN 将Q-learning与神经网络相结合，用于解决无限状态空间的问题，即用神经网络代替q-table，并在q-table 的基础上提出两个创新点[14]。

1) 经验回放。由于Q-learning 算法得到的样本前后是相关的，为了打破数据之间的关联性，在网络训练过程中使用经验回放机制。从以往的状态转移中随机采样 (st,at,rt,st+1)进行训练。经验回放可以减少智能体所需的学习经验，解决样本关联性和效率利用的问题。

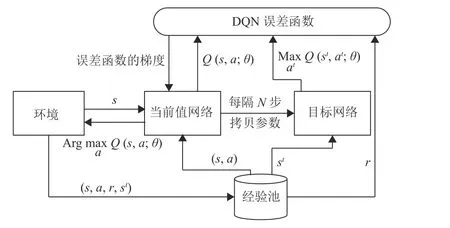
图3 DQN 训练流程

2.2 基于DQN 的下行多小区NOMA 系统设计

本文使用免模型两步训练框架，由于数据驱动算法对数据量要求较高，为了减少在线训练的压力，使用DRL 算法对DQN 进行离线训练；再将训练过的DQN 在真实场景中进行动态微调。基站到用户的下行链路信道可视为一个智能体，环境是下行多小区NOMA 系统，智能体和环境进行交互，智能体选择一个动作at，得到一个奖励rt，进入下一个状态st+1。下行多小区NOMA系统研究的是一个多智能体问题，训练数据及参数较单智能体更为复杂。故引入经验回放技术，经验回放池中包括状态st、动作at、奖励rt和下一个状态st+1等数据，利用经验回放池数据对DQN 网络进行集中训练，分步执行时使用该智能体学习到的策略。

本文将DQN 的思想引入NOMA 系统的功率分配中，即EEPA-DQN 算法，旨在最大化系统的能量效率。EEPA-DQN 的3 个重要组成元素为状态、动作和奖励，具体如下。

状态：状态的选取很重要，为了降低输入维度，在时隙t开始时，智能体根据来自接收机处干扰源的当前接收功率对干扰源按从大到小进行排序。保留前Z个对用户k下一个动作有较强干扰的信息源，Z以外的基站到用户的下行链路及干扰信号的信道增益均视为零。最佳发射功率pt和当前的信道增益gt相关，但这种设计使得DQN 的性能变差。因此，本文基于文献[21]，通过3 个主要特征

奖励：奖励函数的设计决定强化学习算法的收敛速度和程度，智能体目的是最大化的系统的累计收益，若想要让智能体较快的达到目标，提供奖励函数应使智能体在最大化收益的同时可实现系统能量效率最大化。故本文中将系统能量效率用作奖励函数。

3 下行多小区NOMA 系统仿真

3.1 下行多小区NOMA 系统参数设置

本文研究下行多小区NOMA 系统，模拟一个小区数C=16 的蜂窝网络，在每一个小区内配备一个中心基站，每个基站可同时为K=2 个用户服务。假设某一小区的两层之内的小区设置为干扰用户，即干扰层数I=2；用户被随机分配在d∈[rmin,rmax]内 ，rmin=0.01 km和rmax=1 km分别为小区内基站到用户最短距离和最长距离。信道模拟小尺度衰落，小尺度衰落服从独立的瑞利分布，使用Jakes 模型，路径损耗以β=120.9+37.6lgd+10lgz进行模拟，d是基站与用户之间的距离，距离越大路径损耗值越大，z为对数正态随机变量，标准差为8 dB[20]。

为确保智能体能快速做出决策，网络结构不宜过于复杂，EEPA-DQN 算法为一个输入层、两个隐藏层和一个输出层的结构较简单的神经网络。隐藏层采用ReLU 激活函数，输出层的激活函数是线性的。将前12 个小区视为干扰源，功率电平数|A| = 10。为了减少在线计算的压力，采用离线训练。在前100 次迭代训练中，只能随机选择动作，在探索阶段使用自适应贪婪策略[22]。训练得到的EEPA-DQN 具有较强的泛化能力，每次迭代包含1 000 个时隙，每10 个时隙从经验回放记忆中随机抽取一批样本训练EEPA-DQN，使用Adam[23]算法作为优化器，NOMA 无线通信系统参数设置见表1。

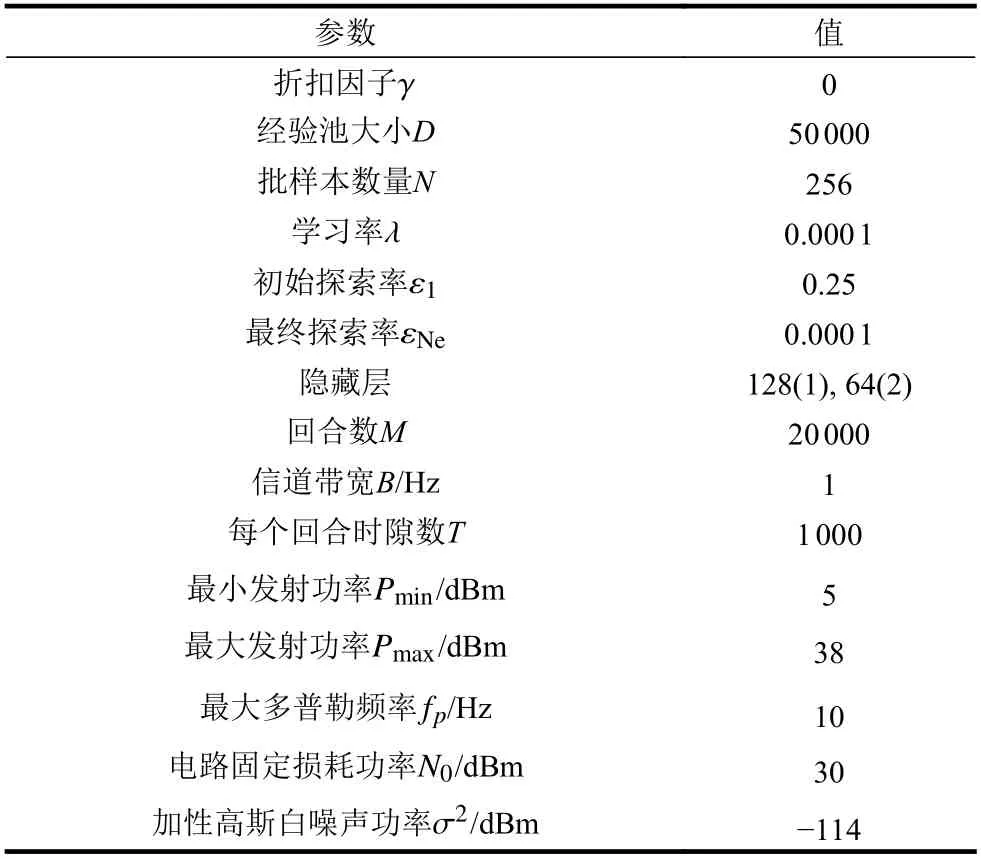
表1 NOMA 无线通信系统参数设置

3.2 功率分配算法比较

在对EEPA-DQN 算法进行实验仿真的同时，将本文提出的EEPA-DQN 算法与FP、WMMSE、MP和RP 算法进行实验比较。FP、WMMSE 这两个算法是非常经典的考虑多小区间干扰的功率分配算法，均为迭代的算法，都需要全局实时的跨小区信道状态信息(channel state information, CSI)，对于基站来说它的开销庞大[24]。深度神经网络具有一定的学习本领，在进行网络的特征提取时具有一定的智能和泛化性能。另一个优点是DQN 的算法复杂度较低。表2 列出了不同算法的单次CPU 运行时间。从表2中可以看出基于强化学习的功率分配算法复杂度较低。EEPA-DQN 算法分别比FP、WMMSE、MP 和RP 算法快13.0 倍、14.1 倍、15.1倍和13.0 倍左右，硬件配置为：Intel(R) Xeon(R)CPU E3-1230 v5；软件为：python 3.7，TensorFlow 1.15.0。仿真的下行多小区NOMA 系统小区数目为16。

表2 单次执行时间

不过，EEPA-DQN 算法计算复杂度与神经网络的层数呈线性关系，且随着维数的增加，计算变得复杂。图4 展示了EEPA-DQN 算法得到的平均能效比FP、WMMSE、MP 和RP 分配算法有显著提高。因此，EEPA-DQN 算法可有效地最大化系统的能量效率。

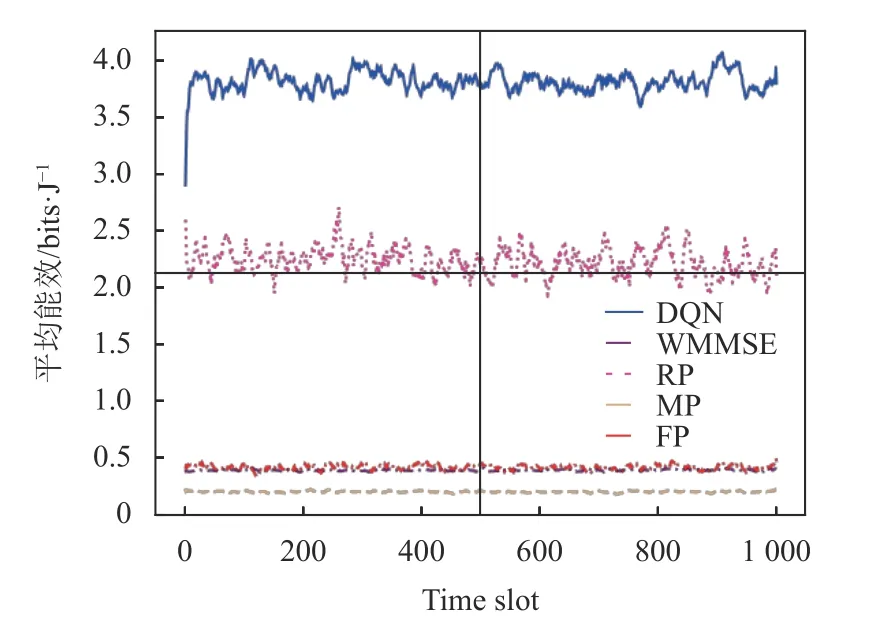
图4 5 种功率分配算法平均能量效率

NOMA 是非正交多址技术，OMA 代表传统的正交多址。当多个用户的信号在相同的信道资源上传输时，NOMA 可以实现更高的频谱效率[25]、更大的系统容量和低传输延迟[26]。从图5 中可以看出，随着迭代次数的增加，两种多址方案的系统平均能量效率都增加了。NOMA 的功率分配与接收端处SIC 过程相关，将较高的功率分配给路径损耗较大的用户，提高了用户的速率，使NOMA 系统比OMA 系统可实现更大的系统平均能量效率，且算法更为稳定。

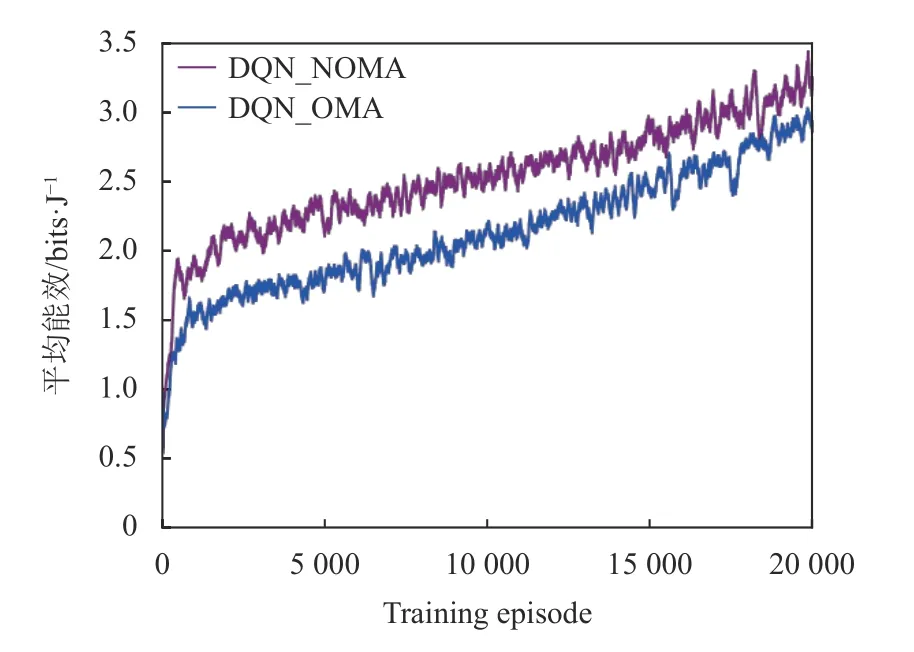
图5 NOMA 与 OMA 平均能量效率

3.3 折扣因子选择

折扣因子是可选择的一个经验值，对于大多数应用而言，增加γ 更有利于DQN。本文算法取γ=0,0.2,0.4,0.6,0.8， 仿真结果表明，γ =0时能效值明显高于其他值，但考虑到信号传输过程中存在路径损耗，智能体与未来回报之间的相关性相对较少，γ 应选取较小的值。图6 仿真了不同γ 值时，EEPA-DQN 训练过程中的下行多小区NOMA 系统平均能量效率，随着训练次数的增加，平均能量效率逐渐增加，且在γ =0时达到最高能效。图7 仿真了不同γ 值在不同小区数时，EEPA-DQN 训练过程中的平均能效。仿真实验考虑了小区数C=9, 16,36, 64 的情况，通过图7 可知，这4 种情况下小区数为9 时所能达到的能效最高，目标小区周围的干扰小区数目越多，外围到目标小区距离越大，干扰会越来越小，所以最外围的干扰小区的干扰功率就非常小。最后仿真了不同小区数目的NOMA 系统的能效。由式(4)、式(5)可知，随着小区数的增加，如小区数为36、64 时，小区间的干扰随之增强，所达到的能效随着小区数量的增加而下降，γ=0 时仍能保持较高的能效，从而验证了本文算法在γ=0 时有一定的泛化性能。

图6 不同γ 值时系统平均能量效率

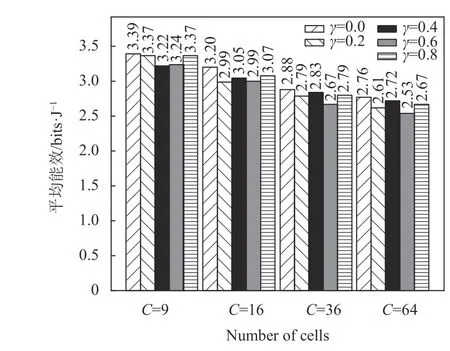
图7 不同γ 值不同小区数时平均能量效率

3.4 学习率

通过实验评估不同学习率对EEPA-DQN 算法的影响。图8 展示不同学习率下的平均能量效率与训练回合的关系，学习率Ir=0.01, 0.001, 0.000 1 这3 种情况，平均能效均有上升趋势。当学习率设置为0.000 1 时，算法相对于其他两个取值更为稳定，且平均能效可达到最高；当学习率为0.01时，可观察到算法稳定性较差。通过以上分析，EEPA-DQN 算法的学习率设置为0.000 1。

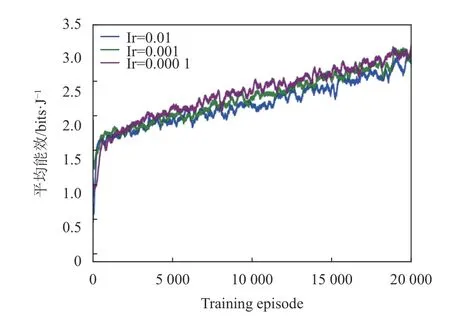
图8 不同学习率值时平均能量效率

4 结 束 语

本文研究了一种基于强化学习的下行多小区NOMA 系统的功率分配问题，旨在最大化系统的能效。由于功率优化问题具有非凸性，本文选用免模型驱动的DQL 算法，将DQL 与神经网络相结合以解决状态连续的问题。仿真结果表明，本文算法将含有两个隐藏层的EEPA-DQN 逼近动作−值函数，同时，本文算法扩展到大规模场景也有较好的性能，但算法的稳定性还有待提高。