一种新型非接触永磁式爬壁机器人设计方案
2022-05-28姜德政任文峰付兴伟赵言正
姜德政,朱 兵,任文峰,付兴伟,2,赵言正
(1.中国长江电力股份有限公司三峡电厂,湖北 宜昌 443000;2.长江生态环保集团有限公司,武汉 430062;3.上海交通大学机器人研究所,上海 200240)
目前,中国水电发电机组的进水压力钢管大多通过人工焊接钢制圆环方式连接而成,具有直径大(一般大于10 m)、行程长(一般大于100 m)、落差高(一般大于40 m)等特点,其表面防腐、焊缝检测等维护作业不仅耗费极大的人力和物力,且存在物资进出场困难、施工周期长等难题。因此,以移动爬壁机器人实现压力钢管的维护作业具有极大的工程意义及市场前景。
爬壁机器人[1]目前已经有较为成熟的发展和应用,其必须具备吸附和移动两个基本功能,其中:移动功能与其他机器人相似,主要包括[2-4]轮式、履带式、腿足式(两足和多足)和轨道式等;吸附功能是爬壁机器人保证运动可靠性的核心,按吸附方式[5-6]可分为负压吸附及磁吸附。 负压吸附一般通过抽气装置在吸附机构内产生负压实现带载吸附,其吸附稳定性主要受抽气装置工作连续性及泄露因素影响;磁吸附[7]方式可分为电磁体式和永磁体式两类,相较而言,永磁体爬壁机器人[8-9]可在磁表面非常小的情况下产生较强的吸附力,更为可靠。
基于某型压力钢管结构特征,提出一种新型非接触永磁式爬壁机器人机构设计方案,重点对永磁式吸附机构进行介绍。通过理论计算,仿真与现场试验验证该设计方案的可靠性及有效性,结果表明该爬壁机器人在压力钢管内进行维护作业时具有较高的可靠性与安全性。
1 爬壁机器人结构总体设计
1.1 设计要求
与常见的路上巡检式移动机器人不同,应用于压力钢管维护作业的移动爬壁机器人一方面需要保证大负载能力以搭载不同作业任务的自动化设备,另一方面还需要具备可靠的吸附能力以适应不同的作业位置。 以某型压力钢管为检测维护对象,如图1 所示。
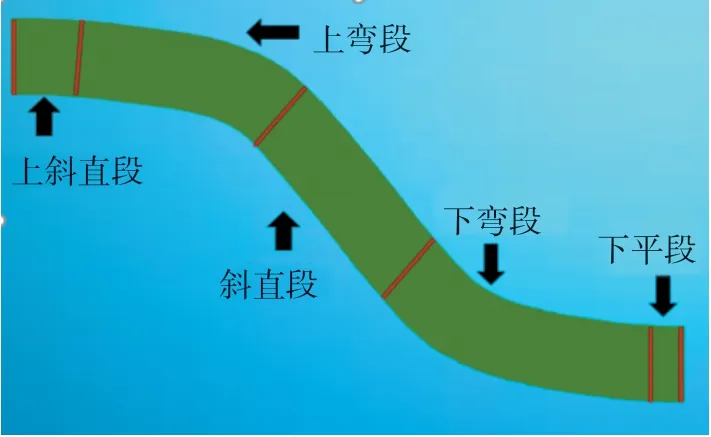
图1 检测维护对象Fig.1 Object of detection and maintenance
某型压力钢管平均直径12.4 m, 平均钢板厚度55 mm,轴线总长度120 m,上下折弯曲率0.062 5。 以200 kg 为目标设计载荷,开展永磁式爬壁机器人设计。
1.2 结构总体设计方案
爬壁机器人结构总体方案如图2 所示。
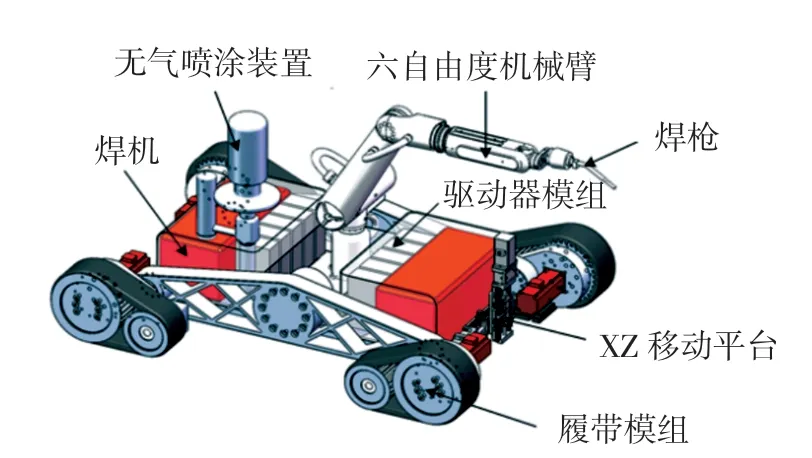
图2 爬壁机器人总体方案Fig.2 Overall plan of wall-climbing robot
爬壁机器人主要由移动平台、机械臂及辅助功能模块组成。其中,移动平台用以实现机器人壁面运动及搭载相关作业设备,其主要由车架、4 个履带模组和1套非接触式永磁吸附模块组成。履带模组的核心部件为伺服电机及履带运动机构, 通过曲轴与车架连接,能够适应曲率半径不同的壁面。 移动平台不包含转向机构,通过履带的差速实现转向。 六自由度机械臂用于实现焊接打磨过程中的作业动作。辅助功能模块包括:无损探伤模块、照明、动力线缆收放及无气喷涂装置。移动平台与机械臂合计约200 kg。辅助功能模块相对爬壁机器人均可视为负载, 在满足作业需求的前提下,总重量不超过200 kg。
吸附模块共由3 组车体吸附装置和4 组履带吸附装置组成。吸附模块分别安装在履带模组的构件下部及车体下部,磁铁与壁面之间为非接触状态。 在机器人进行爬壁作业时,吸附模块与压力钢管内壁不发生接触。
1.3 永磁式吸附模块设计
为保证吸附模块适应压力钢管内壁曲率变化,以非接触式设计思路实现永磁式吸附模块设计, 如图3所示。

图3 新型非接触磁力吸附机构Fig.3 Novel non-contact magnetic absorption mechanism
永磁式吸附装置为永磁铁及轭铁组成的长方体结构,简称磁吸盘。 每个履带模组侧方均安装有1 块磁吸盘。车架底面等间距安装有3 块磁吸盘。所有磁吸盘与壁面非接触,且设计间距不大于15 mm。通过磁场强度分析可知,吸附力与气隙高度的平方成反比。通过安装时手动调节磁吸盘与壁面的间隙,可以调节机器人磁吸附力下限,在维持吸附装置与壁面非接触的前提下,保证吸附过程可靠。
2 吸附可靠性分析
为保证磁吸附爬壁机器人在壁面上平稳工作,需满足两个约束条件[10],即滑落约束与倾覆约束。因此需对爬壁机器人在垂直壁面与倾斜壁面上进行静力分析,通过两个限制条件建立平衡方程求解所需的吸附力。
为简化计算且保证模型尽可能地接近实际问题,进行以下假设:①4 个履带受到垂直壁面的支撑力相同,且每个履带受到均匀的支撑力;②4 个履带的表面材料相同,且爬壁机器人所接触壁面的表面摩擦系数基本相同;③4 个履带侧的非接触吸附装置提供的吸附力相同,且每个吸附装置提供均匀力;④车体上的3个非接触吸附装置提供的吸附力相同,且每个吸附装置提供均匀力;⑤爬壁机器人相对于大直径壁面,计算时将弧形壁面等效于平面。
2.1 爬壁机器人吸附于垂直壁面
2.1.1 滑落约束
为保证爬壁机器人不从垂直平面上滑落,即保证机器人的重力要小于机器人所受的最大静摩擦力。 受力分析如图4 所示。 其中:Ff为机器人所受摩擦力的合力;G 为机器人的重力;Fh为单条履带所受支撑力的合力;NBM为单个车体非接触吸附装置的合力;NTM为单个履带非接触吸附装置的合力。
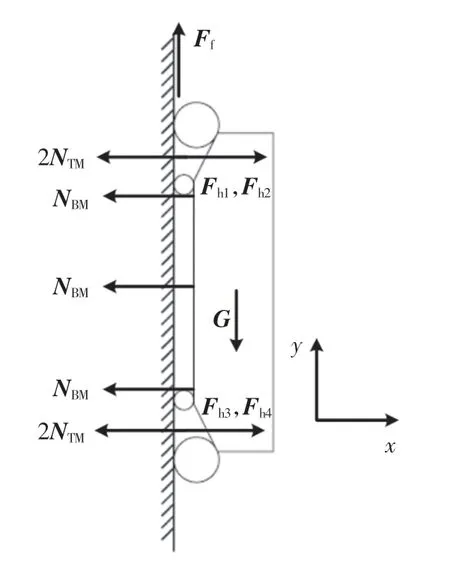
图4 爬壁机器人滑落受力分析(垂直壁面)Fig.4 Force analysis of sliding of wall-climbing robot(vertical wall)
由静止平衡状态受力分析可知,吸附力和支撑力在x 方向上合力为0,即
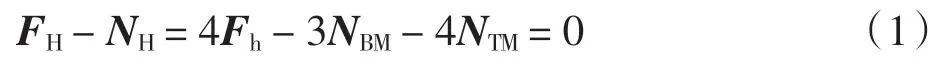
式中:FH为水平支撑力的合力;NH为吸附力的合力。
同时,重力和摩擦力在y 方向上合力也为0,即

又由静摩擦力与压力之间的关系可知

式中μ 为静摩擦系数。 联立式(1)~(3)可得

由验证模型可知:机器人越重,所需要的吸附力越大;摩擦系数越小(表面越光滑),所需要的吸附力越大,均符合实际情况。
2.1.2 倾覆约束
为保证爬壁机器人不从垂直平面上倾覆翻落,即保证机器人的倾覆力矩小于吸附力矩,受力分析如图5 所示。 其中:HG为等效重心与垂直壁面的距离;l1为下履带非接触吸附装置中心与A 点的距离;l2为下履带非接触吸附装置中心与下车体非接触吸附装置中心的距离;l3为下车体非接触吸附装置中心与中间车体非接触吸附装置中心的距离;lW为上下两履带接触中心的距离;lt为每个履带与壁面接触长度。
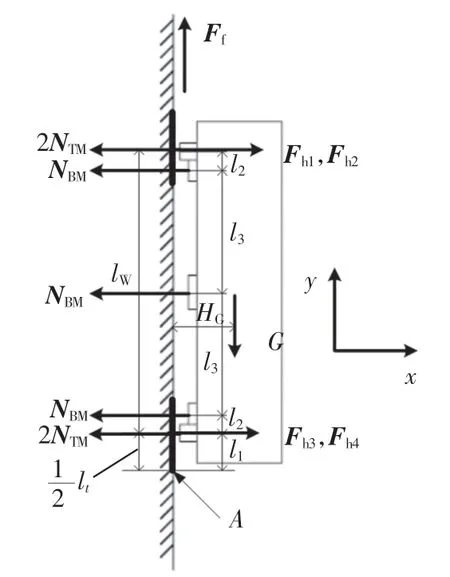
图5 爬壁机器人倾覆受力分析(垂直壁面)Fig.5 Force analysis of overturning of wall-climbing robot(vertical wall)
由图5 可知,要保证机器人正常工作,不沿图中A点倾覆,所以针对A 点建立力矩方程,保证力矩平衡,使得∑MA=0, 倾覆的临界时刻上侧两个履带受到的支撑力为0,所以只要保证上侧两个履带Fh1=Fh2≥0就可以保证机器人不倾覆。 由于假设履带受力均匀和非接触吸附装置吸附力均匀,可将两部分的各个力等效为作用在各模块中心的一个合力。
结合图5 由力矩方程可得
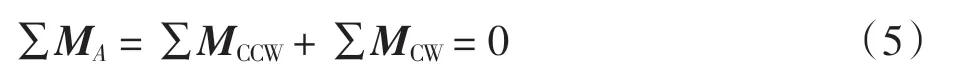
式中
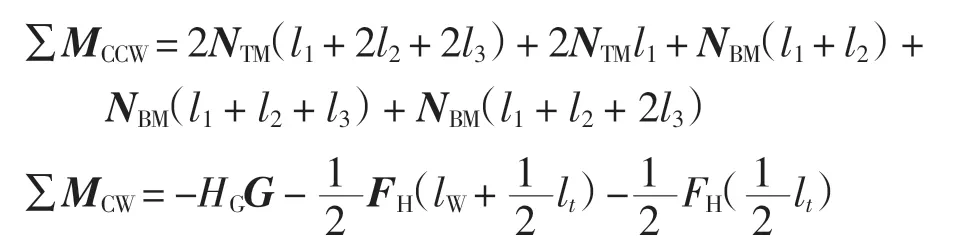
MA为A 点的力矩;MCCW为逆时针方向力矩;MCW为顺时针方向力矩。
发生倾覆的临界点为上面两个履带力Fh1=Fh2=0,即

联立式(2)、式(5)和式(6)可得
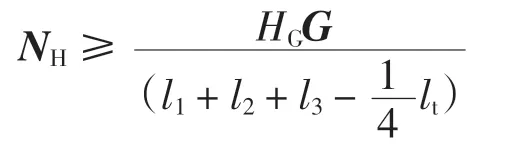
由验证模型可知:机器人越重或重心越高(重心距离垂直壁面越远),所需要的吸附力越大,机器人的结构越长越不容易倾覆,若其他量不变,需要的吸附力越小,均符合实际情况。
综合以上两种情况可知吸附力为
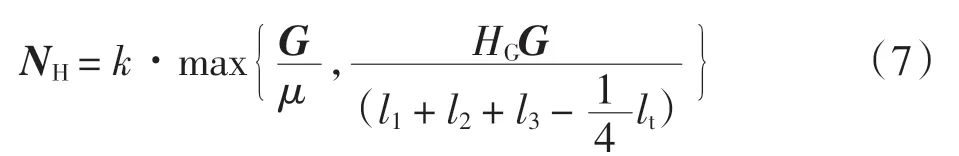
式中k 为安全系数。
2.2 爬壁机器人吸附于倾斜壁面
机器人吸附于倾斜壁面时滑落受力分析如图6所示。 机器人相对于壁面位置如图7 所示。
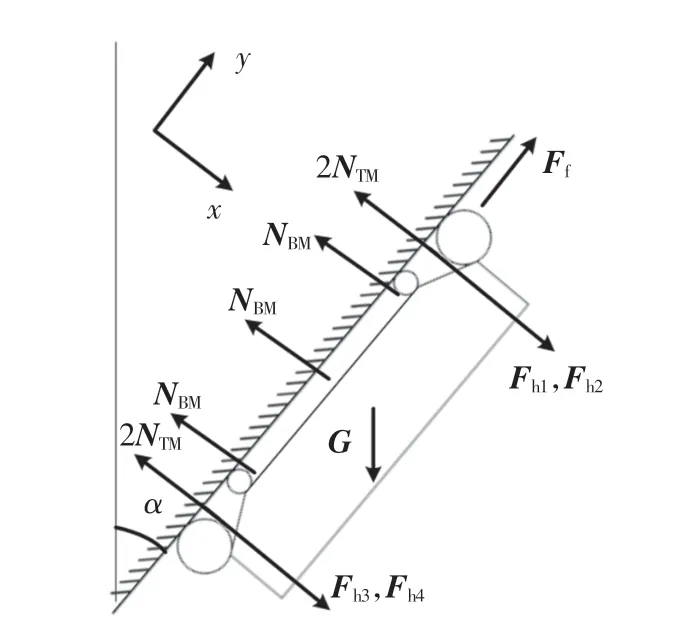
图6 爬壁机器人滑落受力分析(倾斜壁面)Fig.6 Force analysis of sliding of wall-climbing robot(slop wall)
图7 爬壁机器人与壁面相对位置Fig.7 The relative position of the wall-climbing robot and the wall
2.2.1 滑落约束
为保证机器人不从倾斜壁面上滑落,即保证机器人的重力在沿壁面切线方向的分力要小于机器人所受的最大静摩擦力。
由图6 中静力平衡状态受力分析可知,机器人所在坐标系上沿x 方向和y 方向上的合力为0, 其中y方向为机器人前进方向,x 方向为与壁面垂直方向,在此处等效为重心点沿壁面切线方向,即重心点相对于壁面垂直方向。 因此x 方向上合力为0,即

式中α 为机器人与壁面垂直方向夹角。
根据之前的假设可得
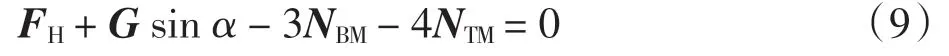
因此,在y 方向上合力也为0,即

又由静摩擦力与压力之间关系为

联立式(8)~(11)可得
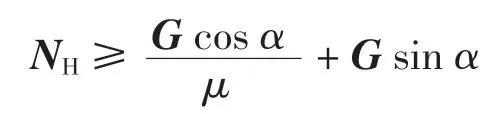
根据以上分析可知:机器人重量越大,所需要的吸附力越大;摩擦系数越小(表面越光滑),所需要的吸附力越大;机器人在壁面上与垂直方向夹角越小,所需要的吸附力越大。
2.2.2 倾覆约束
倾覆时受力分析如图8 所示。
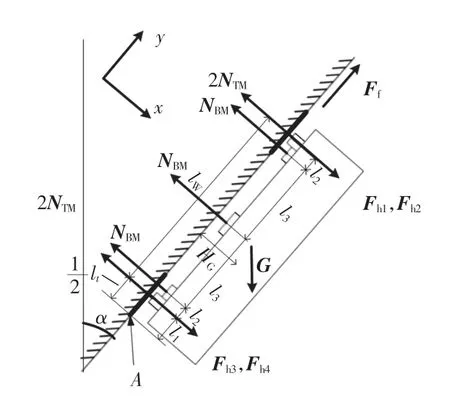
图8 爬壁机器人倾覆受力分析(倾斜壁面)Fig.8 Force analysis of overturning of wall-climbing robot(slop wall)
正常工作时,需要保证机器人不会沿图8 中A 点倾覆,故针对A 点建立力矩方程,由受力分析可知,只要保证上侧两个履带Fh1=Fh2≥0 就可以保证机器人不倾覆。 由于假设履带和吸附装置受力均匀,所以可将二者等效为作用在各模块中心的一个合力。 由力矩方程可得
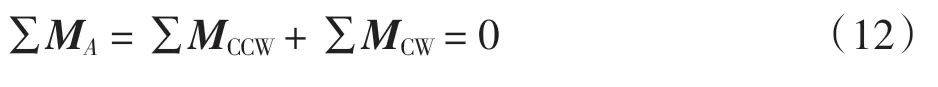
式中
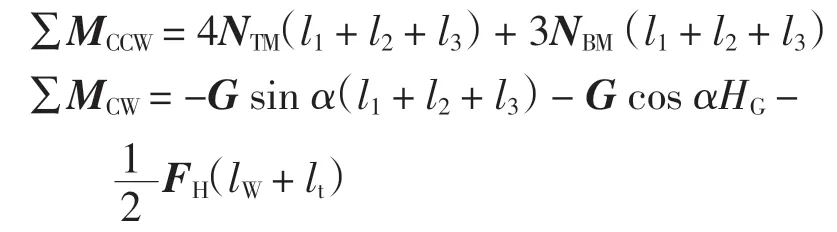
发生倾覆的临界点为上面两个履带受到支撑力Fh1=Fh2=0,若不倾覆要保证

联立式(12)和(13)可得
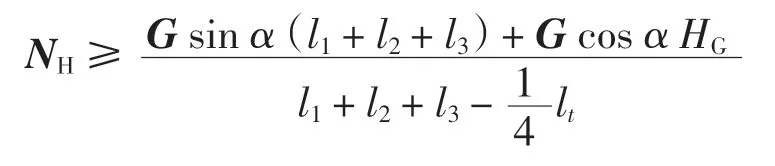
根据以上分析推导可知:机器人越重或机器人重心越高,所需吸附力越大,同时与垂直壁面夹角越小,越容易倾覆;机器人车体越长,越不容易倾覆,此时需要的吸附力相对越小。
结合以上两种情况分析,可以得到机器人需要的吸附力为
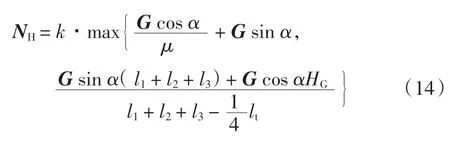
本方案中分别将如下参数代入计算,G=2 500 N,μ=0.6,l1=0.1 m,l2=0.1 m,l3=0.5 m,lt=0.2 m,HG=0.35 m,从而求得所需吸附力大小以及在倾斜壁面上最危险点的角度。
根据式(14)计算得到,当α=37°时最危险,此时最容易滑落,需要的吸附力为4 850 N,即吸附装置至少需要提供485 kg 的吸力。
结合式(7)和式(14)可知,机器人需要k·485 kg 的吸附力。
3 仿真与现场试验结果分析
仿真实验证明在气隙高度为0.1 m 时, 单组履带吸附装置的吸附力可达100 kg,4 组履带吸附装置可产生400 kg 的吸力;气隙高度为0.15 m 时,单组车体吸附装置的吸附力可以达到200 kg,4 组履带吸附装置则可产生600 kg 的吸附力,均可完全可保证机器人的可靠吸附要求。同时吸盘与壁面不接触,没有摩擦力,保证了履带式移动机构运动灵活的优点。现场试验结果如图9 所示。

图9 爬壁机器人不同吸附角度的试验结果Fig.9 Adsorption test results in different inclinations of wall-climbing robot
从图9 中可知,现场试验中爬壁机器人在整圈爬行过程中没有出现滑落和倾覆现象,与理论计算相符合。 图9(a)中,机器人吸附于90°垂直壁面,此时根据计算容易出现滑落现象,但根据现场试验,机器人能够平稳爬行于垂直壁面,证明机器人结构合理,具有充足的吸附能力。图9(b)中,机器人处于127°倾斜壁面,为最危险点,最容易出现滑落现象,但试验机器人平稳经过,证明机器人具备足够大的吸附力。 图9(c)中,机器人吸附于180°水平壁面,即最高点,此时容易出现倾覆现象,但机器人能够顺利经过此点。自此,爬壁机器人在整圈试验中顺利通过各个危险点,进一步说明爬壁机器人设计满足现场需求,能够进行压力钢管内作业。
4 结语
本研究提出一种新型非接触永磁式爬壁机器人设计方案。为实现爬壁机器人在压力钢管内任意位置可靠吸附,介绍了机器人系统结构整体方案,重点给出了永磁式吸附模块的设计方案。针对爬壁机器人在压力钢管内运动的几何位置变化,对吸附力变化情况进行计算并对极限情况下的静力约束条件进行分析。 通过仿真及现场试验证明了永磁式吸附模块有效可靠,爬壁机器人可在大负载情况下实现压力钢管内任意位置的可靠吸附。
