基于集成树类算法估算农田蒸散量
2022-05-28顾信钦吴立峰
顾信钦,吴立峰
(江西省南昌市南昌工程学院水利与生态工程学院,南昌 330099)
0 引 言
蒸散量(ET)是由地表水分蒸发和植物蒸腾2 部分组成,是地面水循环重要的水文过程之一。ET的精确估算有助于合理制定作物的灌溉制度,达到作物高产节约用水的目标,且对干旱监测预警有着至关重要的作用[1,2]。获取ET的方法包括双作物系数法、涡动相关法和机器学习方法等。
双作物系数法得到ET 的前提是正确估算参考作物蒸散量(ET0),计算ET0的方法有Penman-Monteith 模型和Hargreaves模型等。其中Penman-Monteith 公式考虑因素较多,可作为ET0计算的标准方法,但对不能获取完整气象数据的地区并不适用[3]。Hargreaves 模型只考虑温度与辐射参数,形式简洁,但在不同区域使用时差异较大,使用前必须予以校正[4]。涡动相关(Eddy correlation, EC)是直接测量ET的主要方法之一。LIU S M 等报道了在中国海河流域典型下垫面用涡动相关仪测量3年(2008-2010年)的ET,年ET介于430~560 mm[5]。LI S等利用涡动相关仪对2007年中国西北地区覆膜条件下春玉米的ET进行了测定,结果表明日平均ET为2.96 mm/d[6]。虽然EC是目前公认的ET测量标准方法,能够在大范围内准确捕获短期的ET信息[7],但是观测仪器容易受气候影响,数据通常存在大量缺测,且设备昂贵,维护费用高。针对这些问题,使用机器学习方法对ET的研究越来越流行,它们在复杂非线性结构和特性的方面具有强大的能力。DOU X M 等发现4种机器学习模型预测日尺度ET时均表现较好,如在森林生态系统中决定系数(R2) 值介于0.939 8~0.959 3,纳什效率系数(NSE)值介于0.887 7~0.914 7[8]。YAMAÇ S S 等使用了3 种模型来预测意大利南方马铃薯ET,发现当气象数据有限时推荐K-近邻(KNN)模型进行预测,反之推荐使用人工神经网络(ANN) 模型[9]。SHAN X Q 等报道了多元自适应回归样条(MARS)模型预测夏玉米全生育期ET均优于其他模型[10]。CARTER C等在不同生态类型站点比较了10种机器学习(ML)方法预测ET的精度和运行时间,结果表明常绿、灌丛和草地站点的结果最好,湿地站点的结果最差[11]。ABYANEH H Z 等比较了ANN 和自适应神经模糊推理系统(ANFIS)模型的估算值与蒸渗仪测得的大蒜作物蒸散量和作物系数法的估计值,发现ANN和ANFIS适用于预测ET[12]。
基于决策树的机器学习方法,在蒸散量方面得到了广泛的应用[13-16]。目前,关于该类方法在ET 估算方面表现及因子的贡献方面还缺乏系统研究。综上,本文采用了2种基于决策树的机器学习方法XGBoost 和RF 对IT-CA2 和US-CRT 站点不同时间尺度的ET 进行预测,输入数据为2 种数据集,分别是地面通量站观测数据集和ERA 再分析数据集,将气温(TA)、净辐射(Rn)、饱和水汽压差(VPD)、风速(WS)、土壤含水量(SWC)和叶面积指数(LAI)数据按3 种不同组合作为模型输入。研究2 种算法在3 种不同输入组合及2 种不同时间尺度下的预测ET的能力,从而选出适宜的ET预测模型。
1 材料与方法
1.1 随机森林模型
随机森林(RF)是BREIMAN L[17]提出的一种基于Bagging和分类回归树的算法,它使用许多决策树来创建森林。该方法的主要原理是:对于分类器集合h1(X),h2(X),…,hk(X),从随机向量X,Y的分布中随机抽取训练数据集,边际函数表示如下:
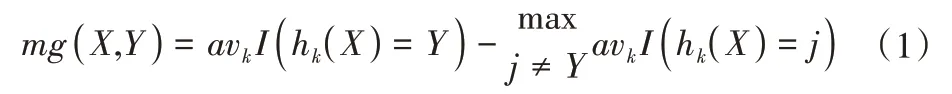
式中:I(.)为指示函数,这个边际函数描述了在X,Y上分类正确的平均投票数超过分类为其他任何类别的平均票数的程度。
1.2 极端梯度提升模型
极端梯度提升(XGBoost)是由CHEN T Q 和GUESTRIN C[18]提出的一种新的算法。该模型基于“提升”的思想,其目的是通过将一组弱学习者的所有预测结合起来,通过特殊训练培养出一个强的学习者。该模型具有并行计算的特点,以提高计算速度。其表示方式如下:
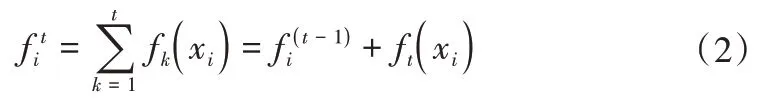
式中:ft(xi)为步骤t的学习值;fit和fi(t-1)是步骤为t和t-1 的预测值;xi是输入变量。
XGBoost 算法每次分裂构建CART 树时,为了在一定程度上降低模型的过拟合,选取使得Gain值最大的节点进行分裂。其中,Gain表示目标函数在每次分裂后信息增益,百分比越高意味着预测参数越重要,计算公式如下式。Cover 表示与此参数相关的观测次数的覆盖度量,由统计获得。
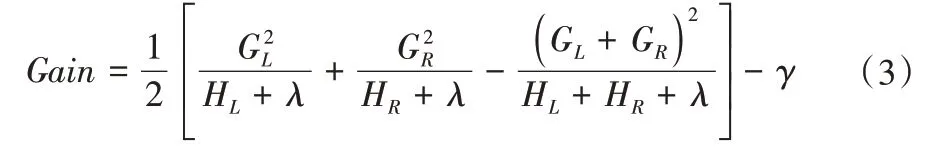
式中:γ和λ是调整参数,用于防止模型过拟合;GL,GR分别为分裂时左右叶子一阶梯度统计和;HL,HR为左右叶子节点二阶梯度统计和的信息增益。
1.3 数据来源
本文选取了2 个农田站点IT-CA2 和US-CRT 进行研究,数据来源于全球通量网https://fluxnet.org/data/fluxnet2015-dataset/,站点的基本信息如表1所示。其中,IT-CA2 站点种植的作物为牧草[19]。US-CRT 站点在2年研究期内,分别于2011年(DOY162-296) 和2012年(DOY141-275) 种植大豆,关于该数据集的详细信息详见CHU H S[20]、XIE J[21]和NOORMETS A[22]。

表1 站点信息Tab.1 Site information
模型的输入数据使用了通量站点的气象观测数据(气温(TA)、净辐射(Rn)、饱和水汽压差(VPD)、风速(WS)、土壤含水量(SWC))和MODIS卫星的叶面积指数(LAI)产品数据(MOD15A2)以及ERA-Interim 再分析数据。为了评估不同情景下模型的表现,设置了3 个不同的输入组合,组合1 包括地面通量站观测气象数据和MODIS 卫星的LAI 产品数据,组合2 相比组合1 少了LAI 数据。组合3 与组合1 相比,其中TA、VPD和WS为ERA再分析数据(表2)。

表2 不同机器学习模型的输入参数组合Tab.2 Input parameter combinations of different machine learning models
1.4 统计指标
本研究使用了5 个统计指标,分别是均方根误差(RMSE)、决定系数(R2)、平均绝对误差(MAE)、偏差百分比(PBIAS)和最大10%均方根误差(RMSEmax10%)[23]其公式分别如下:

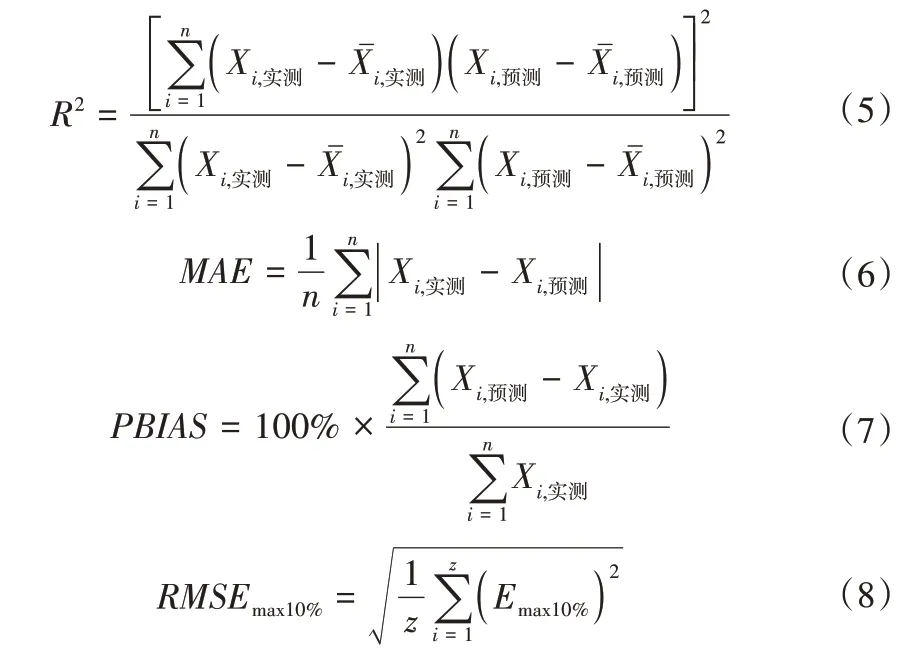
式中:Xi,实测,Xi,预测分别为i处实测值和预测值;,分别为i处实测平均值和预测平均值;n为测试数据的总数;Emax10%为测试数据最大10%绝对误差;z为测试数据总数的10%。
RMSE表现了模型预测值与实测值的不同,模型RMSE值越低越好。R2值越高越好,即越接近1意味这表现越好。MAE和PBIAS可以更好的反应预测误差的实际情况,越低越好。RMSEmax10%用于评价模型在极端条件下的表现。
2 结果与分析
2.1 半小时尺度ET预报精度比较
2种方法在IT-CA2和US-CRT站点的半小时尺度预报精度表现如表3所示。在2 个站点,不同模型的PBIAS均在2%以内,整体上不存在明显高估或低估问题。在IT-CA2 站点,在组合1 和组合3 条件下,2 个机器学习模型的精度比较接近,且均好于组合2。相比组合2,XGB 模型的组合1 和组合3 的RMSE分别下降10%和11%,MAE分别下降了12%和11%;RF模型的组合1和组合3的RMSE分别下降9%和8%,MAE分别下降了9%和6%。从RMSEmax10%指标可以看出,尽管误差最大的10%点的误差相比平均值有所放大,但其值仍在可接受范围内。从散点图可见,XGB 模型与RF 模型的R2值相差很小(图1)。XGB3 的R2值最大为0.85,其次是XGB1(R2值为0.84)和XGB2(R2值为0.81),3 种组合均在实测值大于0.2 mm/h 时,出现一定低估。在RF 模型中,RF1 和RF3 比RF2 的散点更接近1∶1 线,同样实测值大于0.2 mm/d 时,出现一点低估现象。
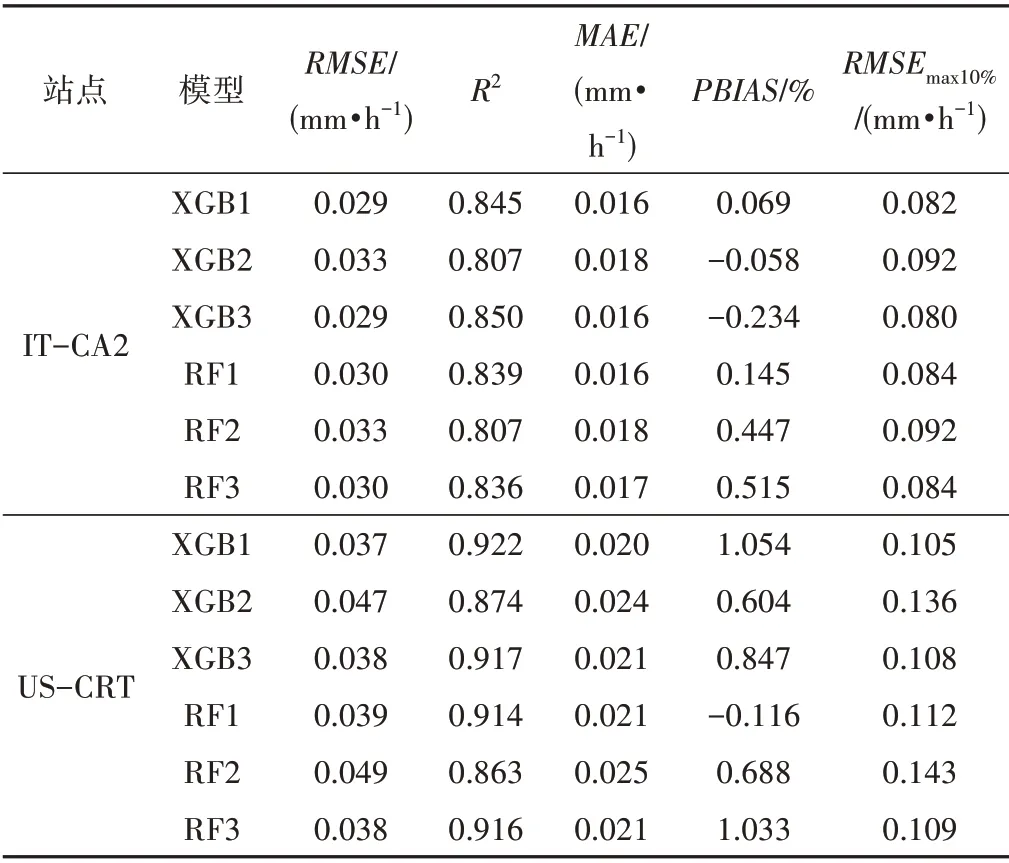
表3 半小时尺度下模型预测的统计指标结果Tab.3 Statistical index results predicted by the model at the halfhour scale at the two stations
在US-CRT 站点,在相同输入组合下,组合3的XGB 模型与RF 模型精度接近;其他组合的XGB 模型相比于RF 模型RMSE和MAE值分别提高了4%~6%和1%~3%。输入组合2时,2 个机器学习模型表现最差。相比组合2,XGB 模型的组合1和组合3 的RMSE都下降2%,MAE分别下降了2%和1%;RF模型的组合1 和组合3 的RMSE和MAE都下降了2%。US-CRT站点的RMSEmax10%稍高于IT-CA2 站点,但在可接受范围内。从散点图可见, XGB 模型与RF 模型的R2值也差别不大(图1),在实测值大于0.6 mm/h 时3 种组合均出现部分低估。XGB1 与XGB3 的R2值相同为0.92,优于XGB2(R2值为0.87)。而RF 模型中,RF3(R2值为0.92)略优于RF1(R2值为0.91),RF2的R2值最小为0.86。
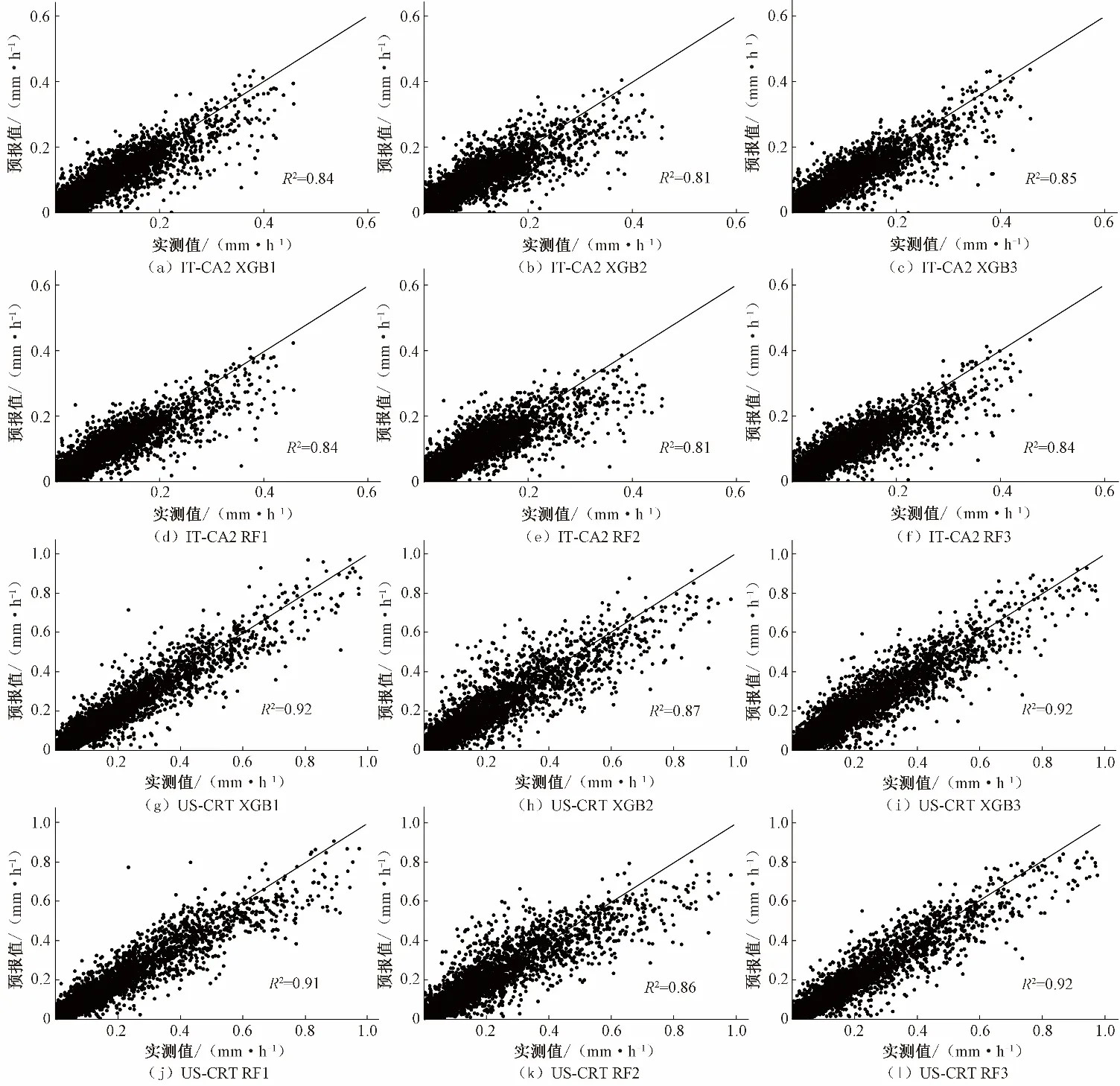
图1 半小时尺度下不同模型ET预报值与实测值散点图Fig.1 Scatter diagram of ET forecast value vs.measured value under different models in half an hour scale at two stations
2.2 日尺度ET预报精度比较
2种方法在IT-CA2和US-CRT站点的日尺度预报精度表现如表4所示。在2 个站点,不同模型的PBIAS均在5%以内,在整体上与半小时尺度一样都不存在明显高估或低估问题。在IT-CA2 站点,输入相同组合时,XGB 模型较RF 模型RMSE和MAE分别下降了5%~7%和1%~7%。2 种模型的组合3 优于组合1,组合1 优于组合2。相比组合2,XGB 模型的组合1 和组合3 的RMSE分别下降8%和14%,MAE分别下降了7%和14%;RF 模型的组合1 和组合3 的RMSE分别下降7%和13%,MAE分别下降了6%和9%。从RMSEmax10%指标可以看出,2 个模型误差RMSE在1.0 mm/d 以内,其值不会对短期ET模拟造成影响。从图2可见,输入相同组合时,XGB 模型比RF 模型的散点更接近1∶1 线。XGB3 的R2值最大为0.75,其次是XGB1(R2值为0.71)和XGB2(R2值为0.66),3种组合均在实测值大于2 mm/d 时,出现低估现象。在RF 模型中,RF1 和RF3比RF2的散点更接近1∶1线,同样实测值大于2 mm/d时,出现一点低估现象。
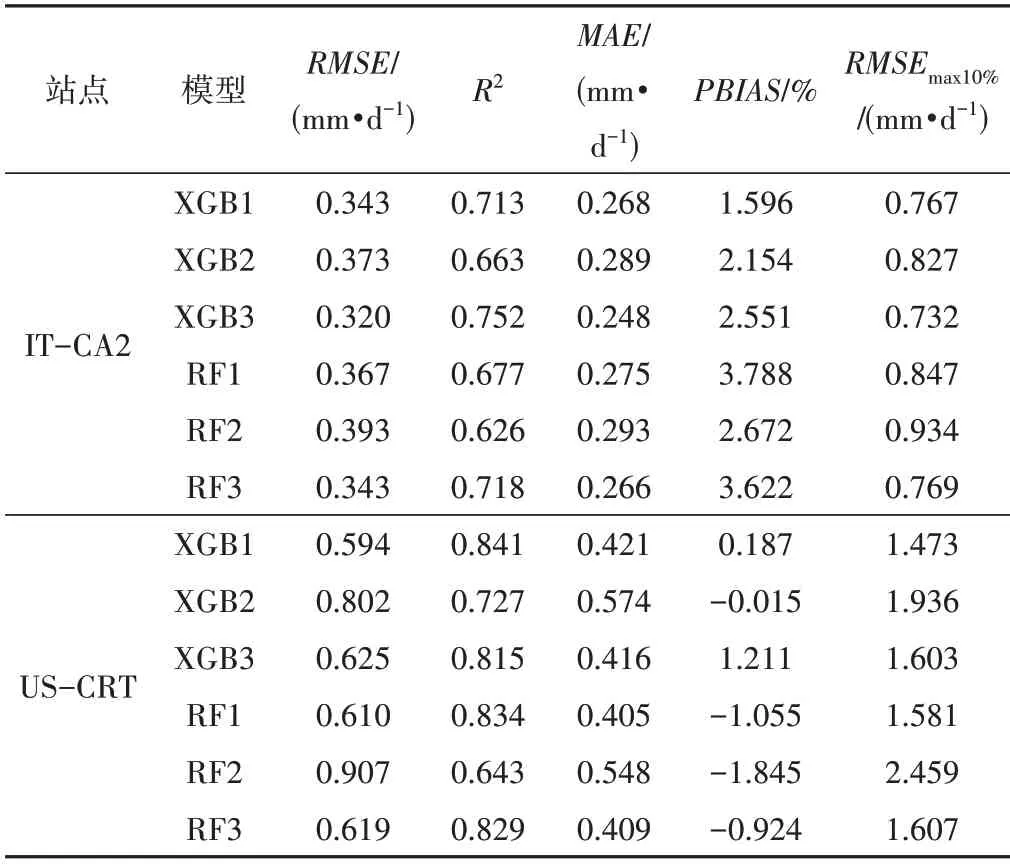
表4 日尺度下模型预测的统计指标结果Tab.4 Statistical index results predicted by the model at the daily scale at the two stations
在US-CRT 站点,在组合1 和组合2 条件下,XGB 模型的RMSE略低于RF 模型。XGB 模型的组合1 和组合3 相比组合2的RMSE分别下降26%和22%,MAE分别下降了27%和28%;RF 模型的组合1 和组合3 相比组合2 的RMSE分别下降33%和32%,MAE都下降了26%。US-CRT 站点的RMSEmax10%值偏大,其误差达1.4 mm/d 以上,可能使短期ET模拟误差升高。XGB模型与RF 模型的R2值差别不大(图2),其中除组合1 和组合2外,RF3的R2值略大于XGB3。3种组合在实测值大于4 mm/d时均出现一定低估。在XGB 模型,XGB1 的散点最接近1∶1线,其R2值为0.84,XGB2和XGB3相比于XGB1,R2值下降了14%和3%。而在RF模型中,RF2和RF3相比于RF1,R2值下降了23%和1%。
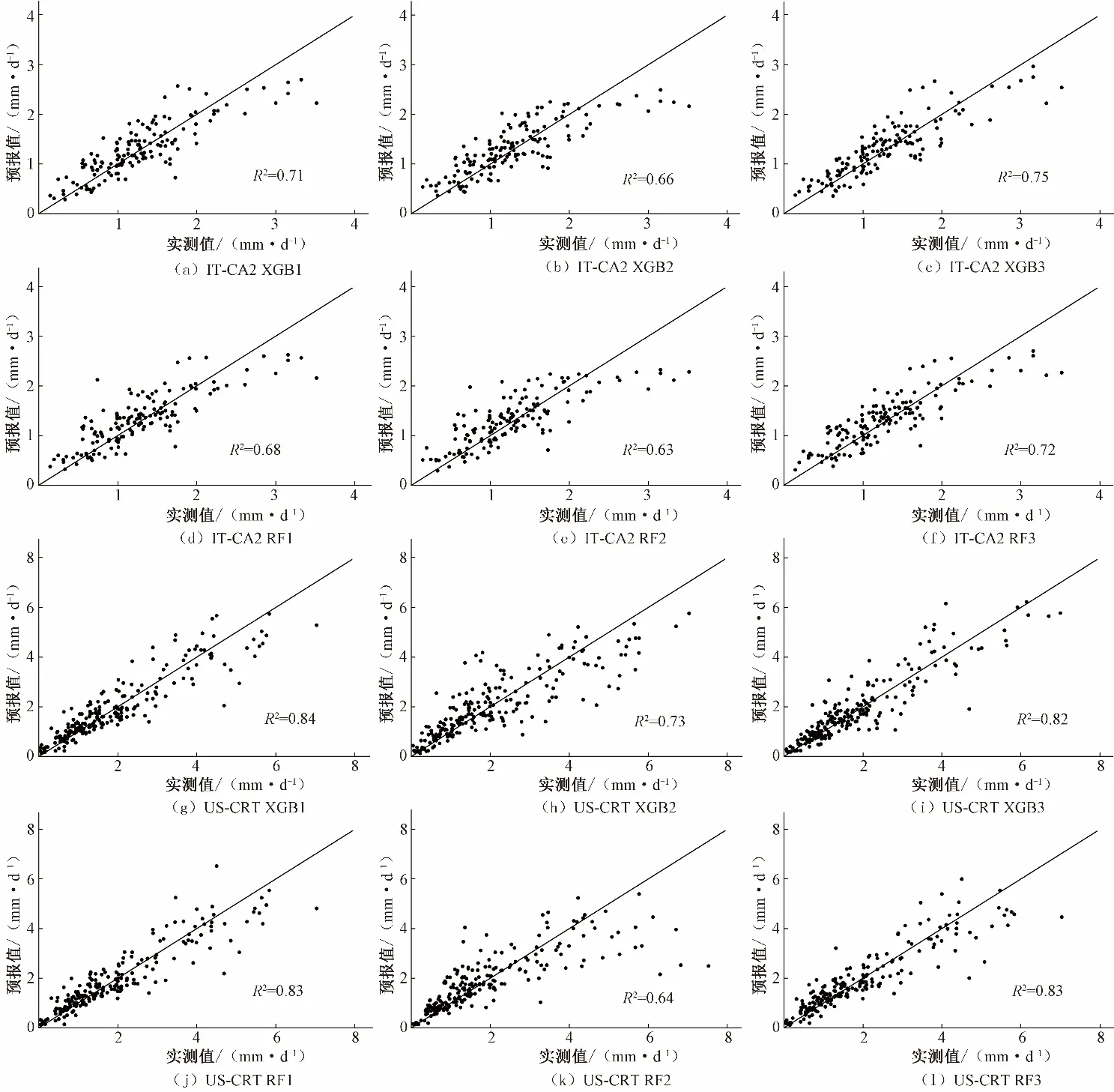
图2 日尺度下不同模型ET预报值与实测值散点图Fig.2 Scatter plots of ET forecast values vs.measured values of different models at the daily scale at two stations
2.3 气象因子对ET预报贡献度比较
为更好地认识不同站点在不同时间尺度下输入气象因子进行ET预报时的贡献度情况,通过算法对气象因子预测ET的重要性评分,绘制IT-CA2站点半小时尺度下的气象因子与ET之间关系图(如图3所示)。Rn 的贡献度最大,Gain值为0.758。除Rn外,气象因子贡献度从高到低依次是SWC、LAI、TA、VPD 和WS (Gain值为0.056、0.055、0.050、0.042 和0.040)。
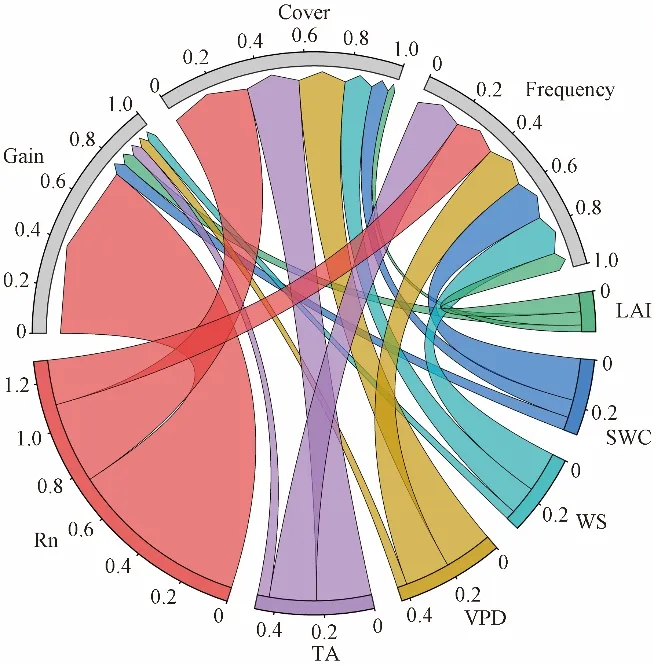
图3 IT-CA2站点半小时尺度下的输入因子与ET之间关系Fig.3 Relationship between input factors and ET at the half-hour scale of IT-CA2 stations
IT-CA2 站点日尺度下的气象因子与ET之间关系如图4所示。Rn 的贡献度最大,Gain值为0.610。除Rn 外,气象因子贡献度从高到低依次是TA、WS、VPD、SWC 和LAI(Gain值为0.099、0.096、0.077、0.062 和0.055)。与半小时尺度的贡献度排序相比,日尺度因子贡献有所不同,但贡献最高的仍是Rn。
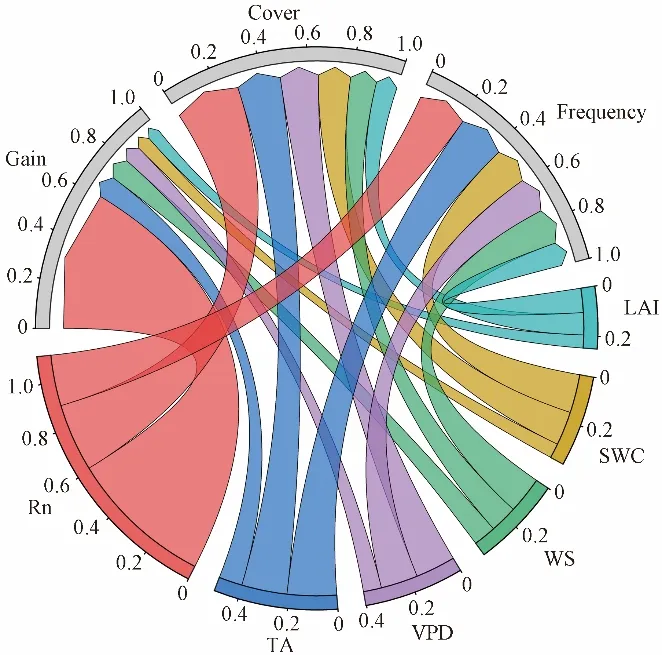
图4 IT-CA2站点日尺度下的输入因子与ET之间关系Fig.4 Relationship between input factors and ET at daily scale of ITCA2 stations
US-CRT 站点半小时尺度下的气象因子与ET之间关系如图5所示。气象因子贡献度从高到低依次是Rn、TA、WS、VPD、SWC 和LAI (Gain值为0.688、0.167、0.054、0.043、0.024和0.023)。
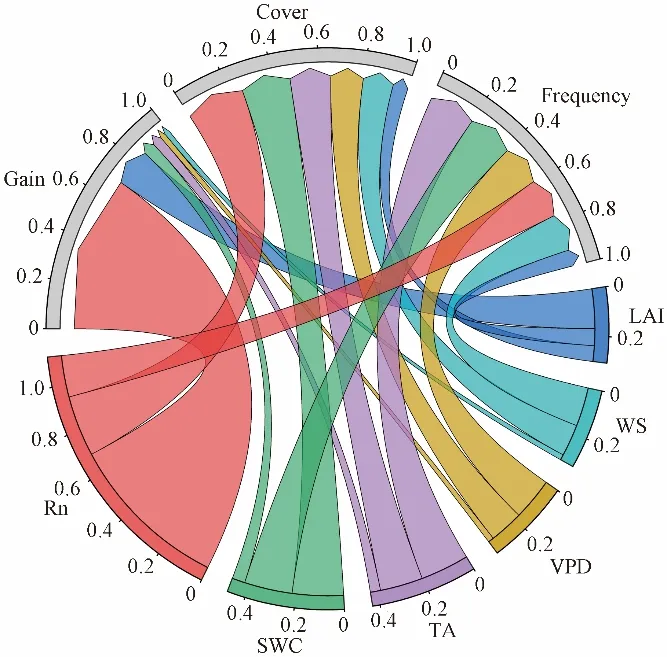
图5 US-CRT站点半小时尺度下的输入因子与ET之间关系Fig.5 Relationship between input factors and ET at the half-hour scale of US-CRT stations
US-CRT站点日尺度下的气象因子与ET之间关系如图6所示。气象因子贡献度排序与日尺度稍有不同,从高到低依次是TA、Rn、LAI、SWC、VPD 和WS(Gain值为0.455、0.278、0.147、0.055、0.038和0.026)。
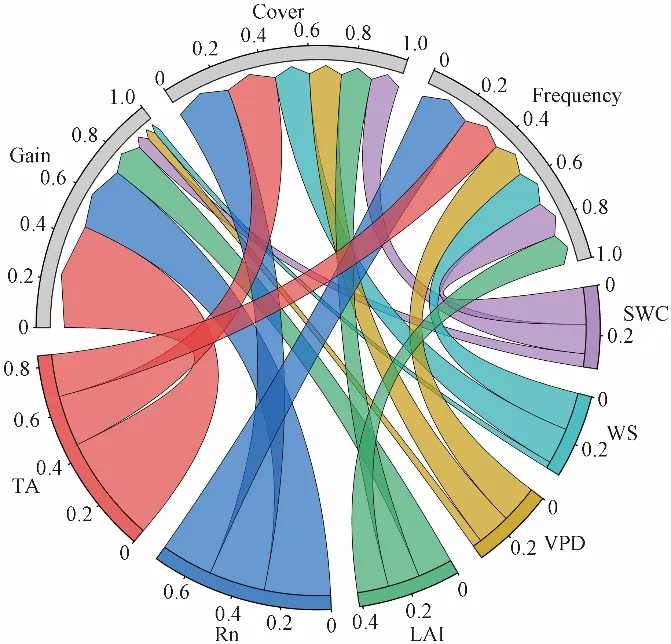
图6 US-CRT站点日尺度下的输入因子与ET之间关系Fig.6 Relationship between input factors and ET at daily scale of US-CRT stations
3 讨 论
机器学习在ET预测方面具有较高精度,但不同机器学习方法的精度有所不同。DOU X M 等报道了不同模型有其最优的适用环境,如在草地和农田站点上人工神经网络模型的表现最好,而在森林和湿地站点上混合极端学习机模型预测ET精度最优[8]。CARTER C 等发现核岭回归模型可以在较小的训练数据集上获得最佳性能,而在数据集较大的情况下,提升树方法最优[11]。本研究结果显示,在半小时尺度下XGB 模型的3种组合均优于RF 模型。在日尺度下,IT-CA2站点的XGB模型也均优于RF,而在US-CRT 站点XGB3 精度略低于RF3。综合评估2 个时间尺度预测ET的能力,XGB 模型可为准确估算ET提供参考。
ERA 再分析数据的精度在国内外得到了广泛的研究,PAREDES P 等报道了ERA 再分析数据计算的ET0在未经过偏差矫正时与Penman-Monteith 公式计算的ET0有很强的相关性(R2>0.80),但存在一定的高估[24]。SRIVASTAVA P K 等发现ERA 再分析中期数据和中分辨率成像光谱仪(MODIS)得出的ET0比美国国家环境预报中心(NCEP)估算的所有季节ET0更准确[25]。本研究结果显示,在输入组合1 和组合3 时,2 种模型的精度都十分接近。可见ERA 再分析数据与地面通量站观测的数据的差异对模型模拟没有明显影响,鉴于ERA 数据在时间尺度和空间尺度上的优势,该数据集具有广泛应用于ET估算的潜力。
4 结 语
本文研究了2种基于决策树的机器学习方法XGBoost和RF对2个农田不同时间尺度ET的模拟情况,得出的结论如下:
(1)在半小时尺度下,输入相同组合时,XGB 模型整体上优于RF 模型。输入组合1 和组合3 时,2 个站点的2 个机器学习模型的精度比较接近,且均好于组合2。2 个站点模型的PBIAS均在5%以内,整体上不存在高估或低估现象。
(2)在日尺度下,输入相同组合时,与半小时尺度相同,XGB 模型整体上优于RF 模型。2 个站点的2 个机器学习模型输入组合1 和组合3 时精度相差很小。2 个站点模型的PBIAS均在5%以内,整体上不存在高估或低估现象。与IT-CA2 站点不同,在US-CRT 站点的RMSEmax10%达1.4 mm/d 以上,可能使短期ET模拟误差升高。
(3)在IT-CA2 站点半小时尺度和日尺度的因子贡献度排序不同,但贡献度最大的因子均为Rn,其Gain值分别是0.758和0.610。在US-CRT 站点上2 个尺度的因子贡献度排序也不同,半小时尺度从高到低为Rn、TA、WS、VPD、SWC 和LAI,日尺度从高到低TA、Rn、LAI、SWC、VPD和WS。
