不同含量砾石嵌套对红壤入渗特性的影响
2022-05-28叶瀛韬李占玲
叶瀛韬,李占玲,王 蕙
(1.中国地质大学(北京)水资源与环境学院,北京 100083;2.浙江水利水电学院水利与环境工程学院,杭州 310018)
0 引 言
土壤水分入渗是水分通过地表向下流入土壤的运动和再分布过程,是大气降水、地表水、土壤水、地下水相互转化的重要环节之一。研究土壤水分入渗不仅是非饱和土壤水分运动和溶质运移等基础理论的重要内容,也是开展土壤侵蚀评价等实际工作的重要科学依据[1,2]。土壤特性是影响土壤水分入渗能力的重要因素,其中土壤中砾石(平均粒径大于等于2 mm 的矿物颗粒)的存在会改变土壤容重、层次结构、孔隙度、土壤含水量、地表土壤结皮等土壤特性[3,4],从而改变坡面产流、入渗、水土流失等过程[4-7]。
存在于土壤表层的砾石会影响土壤的物理特性与水力特征,进而对土壤入渗规律产生影响。一般而言,位于土壤表层的砾石会增加地表粗糙度,改变过水断面大小,影响土壤水分的运移通道,使得含砾石土壤的入渗较均质土壤更为复杂[8]。国内外很多学者对不同地区含砾石土壤的入渗过程开展了大量研究。在宁夏中部旱区,白一茹等[9]通过垂直一维定水头法研究不同砾石覆盖厚度对土壤入渗过程的影响,发现土壤入渗速率、累积入渗量均与砾石覆盖厚度呈正相关关系;在北京山区,符素华等[10]研究发现,地表砾石存在能减缓土壤结皮的形成,促进降雨入渗,使得径流量随地表砾石覆盖度的增加而减少;在三峡库区,王小燕等[11]通过人工降雨方法模拟不同砾石覆盖度对降水入渗速率的影响,指出地表存在的砾石能明显影响土壤水文过程,促进土壤的入渗,其中随着砾石覆盖度增加,土壤稳定入渗速率及稳定入渗系数呈增长趋势。在西非地区,Valentin 等[12]对土壤入渗率与含砾石地区的差异性进行了研究,发现干旱区的土壤入渗率与砾石覆盖度呈负相关关系,而湿润区的土壤入渗率与砾石覆盖度呈正相关关系。在新墨西哥州东部,Wilcox 等[8]研究发现,当研究地面为裸地或耕地地表时,随着土壤中的砾石含量的增加,土壤入渗水量明显增加。以上研究表明了砾石存在对土壤入渗影响的复杂性,也说明了开展不同地区不同砾石嵌套条件下土壤入渗规律研究的必要性。
由于传统研究土壤入渗过程的方法耗时耗力,因此在获取土壤水分入渗的野外或室内实验数据的基础上,通常需要进一步采用理论模型进行拟合,以便通过短历时的测量数据求得长历时的土壤入渗性能的变化规律[13]。常用的理论模型包括Kostiakov 模型[14]、Horton 模型[15]以及Philip 模型[16]等。Kostiakov 模型是一种经验模型,因其形式简单、适用性强而被广泛应用,能够较好地反映水分入渗的瞬变阶段过程[17]。在吕文聪等[7]研究的不同粒径砾石覆盖对土壤入渗过程的影响中,Kostiakov 模型较好地反映了含砾石土壤的入渗过程;在王移等[18]研究的红壤耕作措施对土壤入渗机制的影响中也发现,该模型对土壤入渗过程的估算精度较高。Horton模型作为一种经验模型,适用于模拟均质土壤以及土石混合物的入渗过程[13]。胡廷飞等[19]在对砾石覆盖条件下土壤入渗特性的研究中指出,相较其他入渗模型,Horton模型拟合的结果更接近实测值,整体平均相对误差较小;白一茹等[9]在对入渗模型的适应性评价研究中提出,Horton模型能够较精确地描述较长历时的土壤入渗过程,是分析和预测砂田土壤水分入渗过程的适宜模型。对比Horton 入渗模型,Philip 模型中的各个参数具有明确的物理意义,是适用于模拟垂直一维入渗过程的物理模型[20]。王晓颖等[21]通过Philip 入渗模型对北京市大兴区沙壤土的入渗过程进行模拟,取得了较好的拟合效果。上述研究表明,基于不同研究条件下得出的最优入渗模型不具备普遍适用性,也说明了入渗模型适用性评价的重要性。
红壤广泛分布于我国长江以南各省的丘陵、台地及山岗地带[6]。由于南方丘陵地带地势多变,又因红壤黏重、保水能力差[22],导致我国南方红壤丘陵区水土流失严重。因此研究砾石覆盖对红壤入渗特性的影响具有重要的现实意义;虽然上述关于含砾石土壤入渗特性的研究较多,但关于不同砾石含量嵌套条件下红壤入渗特性的定量分析还较为缺乏,因此本文在前人研究的基础上,以曹娥江流域典型红壤为研究对象,采用垂直一维定水头土壤入渗法,测定不同砾石含量(0%、10%、20%、30%)嵌套条件下土壤的入渗过程,分析不同砾石含量对土壤初始入渗率、稳定入渗率、平均入渗率的影响,并基于Kostiakov、Horton、Philip 入渗模型,探讨不同模型对模拟红壤入渗过程的适用性。研究可为深入探讨红壤水分运移过程、丰富红壤水分入渗机制提供基础,同时,也可为促进土壤侵蚀地区水土保持、加强生态修复提供科学依据。
1 研究区概况及研究方法
1.1 研究区概况
研究区位于曹娥江流域上游浙江省中部绍兴市新昌县境内浙中低山丘陵人居环境维护保土区,占地总面积为24 558 km2;采样地(北纬29°29′38″,东经120°56′30″)位于海拔170 m 的位置,坡度为8°~10°。研究区地处亚热带季风气候区,年均气温16.4 ℃,年均降水量1 443 mm,积温5 200~5 810 ℃。
1.2 研究方法
1.2.1 样品的选取与分组
在曹娥江上游研究区域内选择典型红壤种植坡面,收集砾石、红壤作为实验材料。将实验土壤进行风干干燥处理、除去其中的砾石杂草等物质、过筛处理。结合测量仪器实际情况,将实验中使用砾石的粒径设计为6~25 mm(4~10 mm,10~20 mm,20~25 mm,配比为3∶5∶2),配制10 cm 厚度均匀砾石嵌套的红壤覆盖层。本实验共分为4 个土壤入渗实验组,分别为:未嵌套砾石的均质红壤对照组,表层覆盖有嵌套砾石的红壤覆盖层实验组(砾石含量分别10%、20%、30%)。
1.2.2 垂直一维定水头土壤入渗法
本实验为室内模拟入渗研究,采用垂直一维定水头入渗实验方法进行土壤入渗测量。实验中使用的土柱高度为60 cm,直径30 cm,厚度1 cm,外部贴有标准直尺,以便于观测湿润锋的运移情况,马氏瓶由有机玻璃管制成,细管处贴有标准直尺,直径为19 cm,高度为120 cm,通过变流量为环式入渗土柱提供常水头供水,保证环式入渗土柱处于稳压入渗以及测定环式入渗土柱的进水量(图1)。
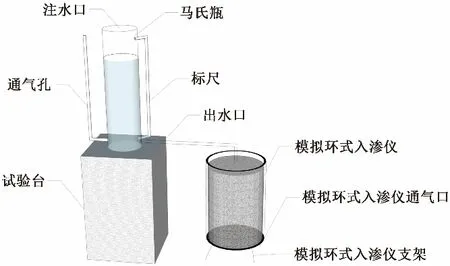
图1 实验装置图Fig.1 Experimental device
用精度为0.01 g的电子秤称出3 cm水头,然后一次性加入环内,同时按下秒表记录入渗时间,立即打开马氏瓶出水口阀门进行供水,维持环内恒定水头。实验前10 min 每1 min 记录一次马氏瓶的水面高度和湿润锋的位置,10~20 min每2 min记录一次,20~150 min 每5 min 记录一次,每个组重复3 次实验,取各组数据的平均值作为实际值。
平均入渗率计算公式:

式中:i为平均入渗率,mm/min;ΔH为马氏瓶内水位的变化;S为马氏瓶的横截面积,cm2;Δt为入渗时间,min;A为入渗环的横截面积,cm2。
1.2.3 入渗模型
为深入探讨砾石含量对红壤入渗性能的影响,在分析过程中引入多个入渗模型拟合不同含量砾石红壤水分入渗的过程,以期获得能够模拟红壤中水分入渗过程的最优模型。具体模型如下:
Kostiakov模型:

Horton模型:
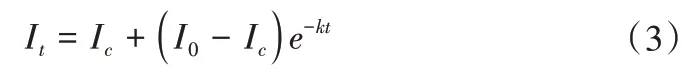
Philip模型:

式中:It指土壤入渗率,mm/h;a、b为Kostiakov 模型经验系数,决定入渗曲线形状,0<b<1;t指土壤入渗时间,h;Ic指土壤稳渗率,mm/h;I0指土壤初渗率,mm/h;k为Horton 模型中土壤入渗参数;S为Philip 模型的吸渗率,mm/h;A为Philip模型常数,mm/h。
各类模型对红壤入渗过程的拟合效果用回归方程中的决定系数和相对误差来表示。决定系数越大、相对误差越小,表明模型拟合的效果越好。
2 结果分析与讨论
2.1 土壤入渗特性分析
初始入渗率、稳定入渗率和平均入渗率是评价土壤水分入渗常用的3 个指标[13]。图2给出了不同砾石含量嵌套条件下土壤水分入渗率随时间的变化曲线,表1给出了土壤水分入渗特性汇总表。可以看出,不同含量(0%、10%、20%、30%)砾石嵌套条件下的土壤初始入渗率都很大(表1和图2)。在入渗初期,砾石含量为20%的红壤初始入渗率最大,达到0.790 mm/min,无砾石红壤初始入渗率最小,为0.137 mm/min。通过表1还可以发现,无砾石红壤与砾石含量为10%的红壤初始入渗率呈显著性差异(P<0.05),砾石含量为10%与含量为20%、30%的红壤也存在显著性差异,但砾石含量为20%的与含量为30%的红壤并未表现出显著性差异,即砾石含量为10%时,砾石嵌套对土壤初始入渗率有显著影响(P<0.05)。
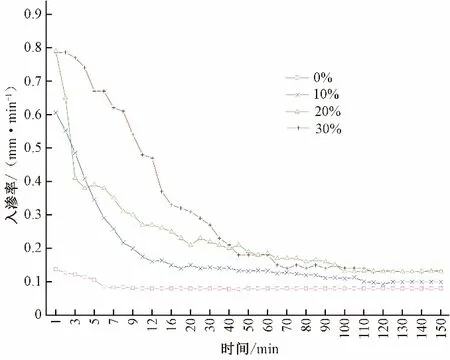
图2 不同砾石含量红壤瞬时入渗率变化Fig.2 Changes of instantaneous infiltration rate of red soil with different gravel contents
随着时间的推移,水分的不断渗入,土壤含水率增大,土水势升高,土壤团聚体膨胀后裂隙减少,加之原状土表面细颗粒的堵塞,土壤孔隙度和孔隙连通性变差,透水的物理孔隙减少,入渗率降低,最终达到稳定入渗[23]。砾石含量为10%、20%、30%土壤的稳定入渗率仅为其初始入渗率的16%~17%。土壤入渗过程可以划分为3 个阶段,渗透初期分子力作用下的入渗率瞬变阶段、毛管力和重力作用下的渗漏阶段、重力作用下的稳定入渗阶段。砾石存在对土壤入渗曲线的影响非常明显(图2),随时间的推移,入渗曲线迅速降低,曲线坡度较大,瞬变、渗漏、稳定入渗3个阶段清晰,经过约115~130 min 的入渗后到达稳定入渗率;而无砾石红壤入渗变化曲线变化幅度较小,入渗阶段变化不明显,趋于稳定入渗的时间也很短,在12 min 左右进入稳定入渗。另一方面,无砾石红壤与砾石含量为10%的红壤稳定入渗率未表现出显著性差异(P<0.05),但与含量为20%、30%的红壤呈显著性差异,同时,砾石含量为20%的与含量为30%的红壤也未表现出显著性差异(P<0.05),即砾石含量为20%时,砾石嵌套对土壤稳定入渗率有显著的影响(P<0.05)(表1)。
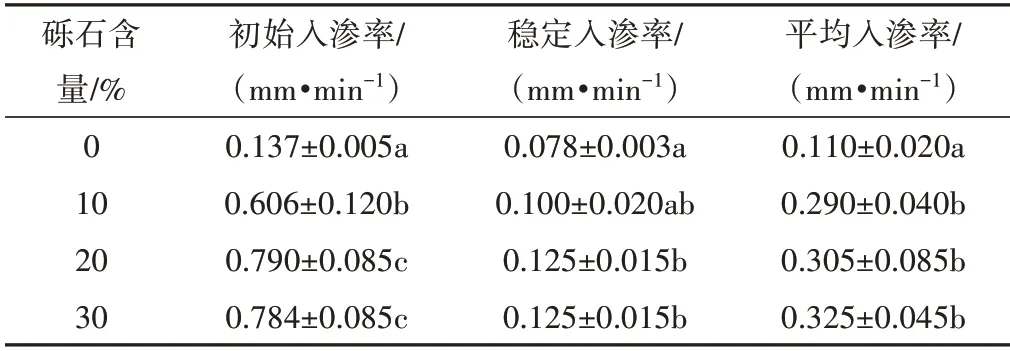
表1 不同砾石含量嵌套的红壤入渗特性汇总表Tab.1 Summary of infiltration characteristics of red soil nested with different gravel contents
平均入渗率是指在土壤入渗过程中,到达稳定入渗率时,土壤水分入渗量与时间的比值。随着砾石含量的增大,土壤平均入渗率呈现上升趋势,无砾石红壤平均入渗率最小,为0.110 mm/min,砾石含量为30%的红壤平均入渗率最大,为0.325 mm/min;无砾石红壤与砾石含量为10%的红壤平均入渗率呈显著性差异(P<0.05),但砾石含量为10%的与含量为20%、30%的红壤并未表现出显著性差异,即砾石含量为10%时,砾石嵌套对土壤平均入渗率有显著影响(P<0.05)。
2.2 土壤入渗模型评价
图3~图5给出了Kostiakov 模型、Horton 模型、Philip 模型对不同砾石含量红壤入渗率的拟合曲线。由图可知,Kostiakov模型对于砾石含量为20%的红壤在75~125 min 时段入渗过程拟合程度较好,对于砾石含量为10%、30%的红壤在10~75 min 时段入渗过程拟合程度较差(图3);模型参数b的变化区间位于0.10~0.43之间,参数a的变化区间位于0.11~1.05之间,a值随砾石含量的增加而增大,表明土壤入渗率的变化增大,入渗率衰减速度增加;模型拟合结果的决定系数达到0.78~0.98。Horton模型对于砾石含量为30%的红壤入渗过程在100~150 min 拟合程度较好,对于砾石含量为20%的红壤在10~100 min 入渗过程拟合程度较差;有研究表明,Horton 模型在土壤水分入渗稳定阶段的模拟精度较高[24],在0~100 min,红壤入渗过程还未达到稳定阶段,因此拟合效果较差(图4)。Philip模型对于砾石含量为20%的红壤在95~150 min 时段入渗过程拟合程度较好,对于无砾石红壤0~95 min 时段入渗过程拟合程度较差(图5);模型参数S的变化区间位于0.13~2.13,随时间进行,A值会成为作用于入渗过程的重要因素,即稳定入渗率,与实测数据比较,拟合的稳定入渗率A值偏小;Philip模型拟合结果的决定系数达0.90~0.99(见表2)。
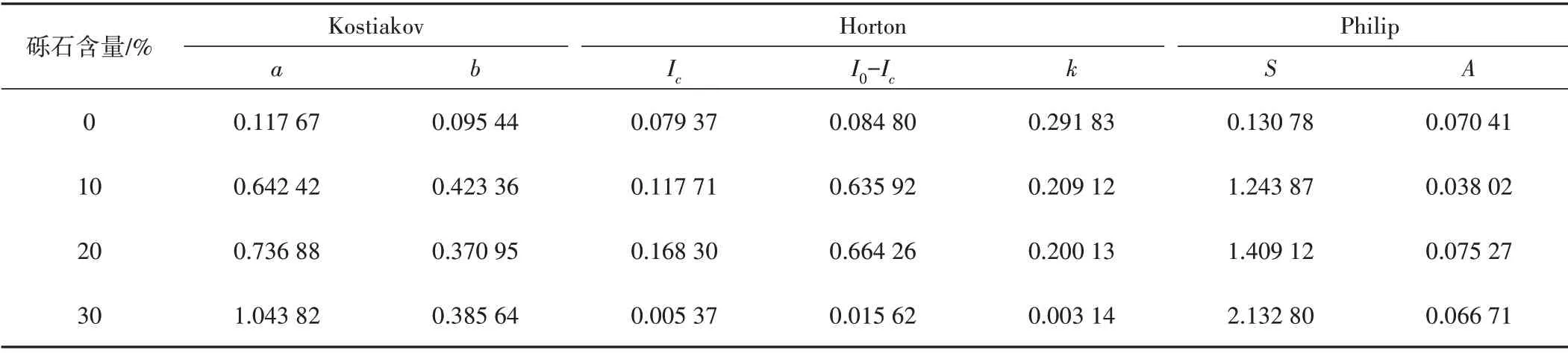
表2 入渗模型拟合参数汇总表Tab.2 Summary of fitting parameters of infiltration models
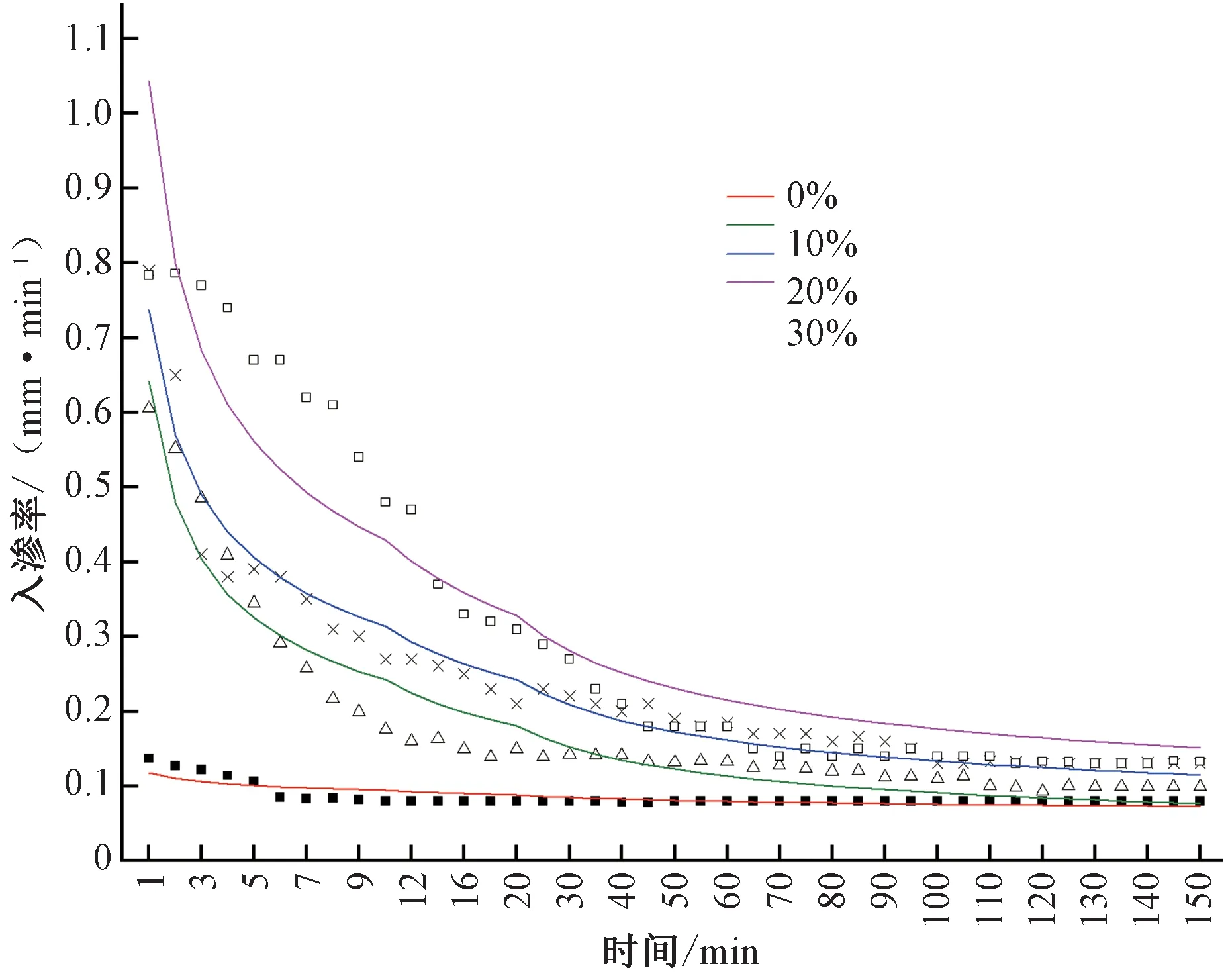
图3 Kostiakov入渗模型关于砾石含量不同红壤拟合曲线图Fig.3 Fitting curve of Kostiakov infiltration model on red soil with different gravel contents
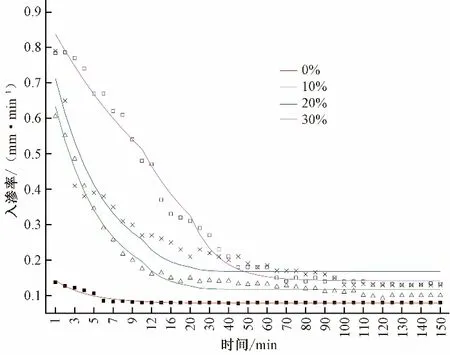
图4 Horton入渗模型关于砾石含量不同红壤拟合曲线图Fig.4 Fitting curve of Horton infiltration model on red soil with different gravel contents
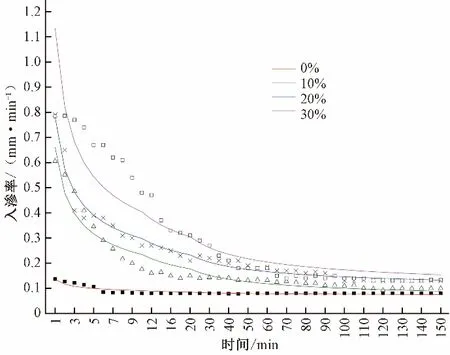
图5 Philip模型关于砾石含量不同红壤拟合曲线图Fig.5 Fitting curve of Philip infiltration model on red soil with different gravel contents
表3给出了不同模型对实验数据拟合的决定系数以及相对误差。可以看出,针对不同砾石含量的实验数据,3种理论模型的拟合效果有所不同,Horton 模型对于无砾石以及含量为10%和30%的红壤入渗过程拟合效果最好,决定系数达0.99,较其他模型均偏高,相对误差分别为10.08% 和6.26%,较其他模型均偏低;Philip 模型对于砾石含量为20%的红壤入渗过程拟合程度最好,决定系数达到0.99,相对误差不到7%;Kostiakov 模型对于各实验组数据的拟合效果均最差,对于砾石含量为30%的红壤入渗过程拟合相对误差高达20%以上。

表3 模型平均误差表Tab.3 Average error of each model
2.3 讨 论
通过实验数据分析发现,不同砾石含量嵌套对应的土壤初始入渗率都很大(表1和图2),这是因为实验初期土壤比较干燥,入渗率受土水势和土壤大孔隙流的控制,土壤越干燥,含水率越小,土水势越低,土壤团聚体间裂隙越多,对水分子的吸力越大,因此初始入渗率就越高[23]。无砾石红壤与砾石含量为10%的红壤初始入渗率呈显著性差异,砾石含量为10%的与含量为20%、30%的红壤也存在显著性差异,但砾石含量为20%的与含量为30%的红壤并未表现出显著性差异,这应该与砾石存在对土壤水分入渗的影响是多方面的有关,土壤水分运动通道随砾石含量增加会更加复杂;一方面,砾石含量的提高会有利于减少土壤细颗粒之间的接触面积,容易形成土壤大孔隙,而一定数量相互联通的大孔隙有助于土壤中优势流的产生,因而促进了土壤的入渗[25];另一方面,砾石含量、砾石在土体中排列方式、砾石与砾石间接触状况等因素,也使得水分入渗路径弯曲复杂,从而延缓土壤入渗[25]。房凯等[26]在其研究中就发现,随着砾石含量的增加,过水断面及水分弯曲流程所产生阻碍作用要大于砾石存在带来大孔隙导致优势流产生的促进作用;因此,土壤初始入渗率并非随着砾石含量的增加而持续上升。
砾石的存在对土壤入渗曲线的影响非常明显(图2),瞬变、渗漏、稳定入渗3 个阶段随时间的推移其变化非常清晰;而无砾石红壤入渗曲线阶段变化不明显,变化幅度较小,趋于稳定入渗的时间也很短。含砾石土壤到达到稳定入渗率的时间较不含砾石土壤更久,这可能是因为随着入渗深度的增加,湿润峰向下运移的过程受嵌套砾石影响逐渐减小的缘故[27]。另外,无砾石红壤稳定入渗率与砾石嵌套含量为20%、30%的红壤呈显著性差异,而砾石嵌套含量为20%的与含量为30%的红壤并未表现出显著性差异(表1);这说明,砾石嵌套对土壤稳定入渗率有一定的影响,随着砾石含量的增加,砾石覆盖度随之增加,土壤水向下移动的压力势呈现上升趋势,相同时段内湿润峰能运移至土壤更深处[11],因此使得含砾石土壤的稳定入渗率大于无砾石土壤;但随着砾石含量的增加,土壤稳定入渗率并非持续上升,这与朱元俊等[28]的发现基本一致;即在砾石含量在20%、30%之间时可能存在一个阈值,当砾石含量低于阈值时,砾石含量增加会不断促进水分入渗,当砾石含量接近或等于阈值时,促进入渗的效果最明显,随后当砾石含量高于阈值时,入渗会随砾石含量增加而减弱[13],因此砾石嵌套含量为20%、30%的红壤的稳定入渗率比较相近。
在对砾石嵌套的红壤入渗过程的模拟研究中,Horton模型和Philip 模型表现较好,其中Horton 模型对于无砾石以及砾石嵌套含量为10%和30%的红壤入渗过程拟合效果最好,Philip模型对于砾石含量为20%的红壤入渗过程拟合效果最好,Kostiakov 模型模拟效果较差。Kostiakov 模型计算方便,但由于其物理意义不明确,因此在很多研究中,该模型拟合效果均较表现不佳[24]。Philip模型是基于Richard理论推导得来,表达式较Kostiakov 模型复杂,模拟效果较好;有研究发现,该模型对于北京市大兴区沙壤土的入渗过程模拟效果很好[21];但Philip 模型对积水入渗、降雨条件土壤入渗和非均质土壤水分入渗过程的模拟精度有待改进,且该模型对参数精确度要求较高[24]。比较而言,Horton 模型在土壤水分入渗稳定阶段的模拟精度较高[23]。樊才睿等[29]研究发现,对呼伦贝尔草原3 种放牧强度草地土壤入渗过程的模拟,均是Horton 模型的模拟效果最好;徐金鑫等[6]研究砾石分布对红壤坡面侵蚀产生的影响时,同样发现Horton 模型能够较好的描述含砾石土壤的入渗;李雪垠等[30]研究表明,Horton模型是分析和预测三峡库区林草覆盖下紫色土中砾石夹层土壤入渗过程的适宜模型。
土壤水分入渗过程是一个复杂的过程,受到多种因素的影响和制约,这里重点关注了不同砾石含量嵌套对红壤入渗过程的影响,实验中选择砾石的配比是固定的,然而,存在于自然界中的砾石的粒径是随机分布的,并非固定不变;另外,实验中仅选用砾石含量作为控制变量,其他因素如实验坡度、土壤类型均视作不变量,未进行多个变量的控制分析,因此,未来还需要对多种不同粒径砾石按不同含量混合对土壤入渗过程的影响作用进行深入研究。
3 结 论
本文以曹娥江上游地区的红壤作为研究对象,将不同含量砾石嵌套至红壤中,探究不同含量砾石嵌套对红壤入渗特性的影响,主要结论如下:
(1)土壤初始入渗率、稳定入渗率、平均入渗率均随嵌套砾石含量的增加呈上升趋势,但并非持续上升;对于砾石嵌套含量为10%的红壤,砾石存在对土壤初始入渗率、平均入渗率有显著性影响(P<0.05);砾石嵌套含量为20%时,砾石存在对土壤稳定入渗率有显著性影响(P<0.05)。
(2)Horton入渗模型对无砾石红壤及砾石嵌套含量为10%和30%的红壤入渗过程拟合效果最好,平均相对误差最小;Philip 模型对于砾石嵌套含量为20%的红壤入渗过程拟合效果最好;Kostiakov 模型对于本研究模拟红壤水分入渗过程的拟合效果较差。
