影响高斯束偏移成像质量和效率的主要因素分析

2022-05-27张志鹏孙章庆韩复兴王雪秋刘明忱高正辉

世界地质 2022年2期

张志鹏，孙章庆，韩复兴，王雪秋，刘明忱，高正辉

吉林大学地球探测科学与技术学院，长春 130026

0 引言

地震波正反演的解决方法可分为波动理论和射线理论。波动理论计算速度慢，计算机硬件要求高，结果准确。射线理论方法计算速度快，计算机硬件要求低，结果符合预期，已广泛应用于地震波正演模拟、偏移成像和层析速度反演等方面。

渐进射线理论(ART)出现在20世纪50年代，前苏联学者Babich, Karal和Keller在弹性波领域中利用现有的电磁学研究成果提出了弹性动力学波动方程的级数解[1]。随后，Cerveny, Ravindra, Cerveny, Hunyga, Kravtsov和Orlov等又展开更深入的研究并对渐进射线理论的的发展做出了巨大贡献[2]。然而,射线方法具有许多问题，不仅对介质的近似以及模型的微小细节方面非常敏感，而且在其动力学特征方面也存在难以在射线焦散区、阴影区等区域获得正确的振幅等缺陷[3]。

针对常规射线追踪存在的问题，相关学者发展了高斯束方法，高斯束偏移方法既使用动力学射线追踪，使波场不存在奇异性区域，弥补了传统射线方法的缺陷和不足，又具有一定的有效宽度，弥补了两点射线追踪费时的不足，提高了计算效率[4]。首先高斯束相比常规射线方法，不用再进行两点射线追踪，且对模型的速度误差不敏感[5]。其次，因为高斯束相比常规射线方法具有复值的动力学射线追踪参量，所以不会产生射线奇异性区域，有效解决了射线方法中的焦散问题[6]。

首先，在实现高斯束偏移成像的过程中，由于诸多射线参数对高斯束的影响，高斯束偏移成像的精度与效率往往难以兼顾，为了平衡成像的精度与效率，笔者对高斯束偏移核心参数的选取进行研究。关于偏移成像中的参数优化问题，1997年， Whitmore et al.[7]通过控制各向异性参数，在TI模型下获得了大炮检距下的更好的拟合；2011年，岳玉波[8]就高斯束偏移的参数选择展开了讨论，并给出了部分核心参数的选取；2015年，王华忠等[9]在凹陷模型下对CWI方法的研究中对特征射线参数进行优化进而实现对成像效率进一步提升；2016年，杨继东[10]通过控制Kirchhoff偏移中的偏移参数来研究格林函数的影响，并给出了不同参数下的理论计算结果的对比；2019年，Lyu et al.[11]在时空域高斯束偏移方法的研究中也给出了偏移参数的动态选取，研究不同参数下的偏移成像效果；2019年，吕庆达[12]在Sigsbee2a模型下进行经典高斯束偏移方法与时空域自适应高斯束偏移方法的对比研究中也给出了不同成像参数的数值模拟结果。可见偏移参数的选取是影响成像质量与效率的重要因素；2021年，李勤[13]在对绕射波路径积分成像方法的研究中对不同的速度区间参数选取进行对比，在速度区间选取适中时取得较好的成像效果。参数的选取直接关系到地震成像质量与成像效率。

另外，速度模型需要满足射线追踪系统具有二阶连续的导数，但实际情况下的速度模型极其复杂，具有突变间断面和速度梯度[14]。为解决成像过程中成像精度的难题，对速度模型的光滑处理对偏移成像质量的影响进行了研究。2000年，Gray[15]就过度光滑对偏移成像质量的影响展开讨论，使用加拿大Foothills模型、SEG/EAGE岩丘模型和Marmousi模型3种合成数据模型，得到光滑程度较低的模型会比过度光滑的模型成像质量更好的结论。由此可见，速度模型的光滑程度是影响偏移成像质量的重要因素；2005年，Pacheco et al.[16]对偏移前的速度光滑问题是有利还是有害的问题展开研究，得到根据模型的复杂性和初始速度模型误差的类型和大小，光滑处理可以提高深度偏移成像质量的结论；2010年，白敏等[17]对理论模型和实际模型展开研究，得到深度偏移相比时间偏移对速度误差更敏感的结论；2018年，韩复兴等[18]对PDE算法在模型光滑的处理中对偏移成像的影响展开研究，对比了不同光滑程度的Marmousi模型对射线路径与走时误差的影响，得到PDE算法对速度模型进行处理可以得到更好的偏移成像效果的结论。

关于Kirchhoff偏移中的速度模型光滑问题， 1996年Mispel et al.[19]基于Kirchhoff叠前偏移利用Picrocol模型得到无论速度模型准确与否，光滑的速度模型都足以提供成像质量的结论；2011年Moser et al.[20]通过在包含所有可获得的结构信息的非光滑速度模型中，计算光滑模型中追踪的射线路径的走时进行成像，大大改善了Kirchhoff偏移的深层成像质量，尤其是盐下成像质量；2020年，Zhang et al.[21]在研究Kirchhoff偏移中角度域共成像点道集的提取方法中运用到平滑的Marmousi模型，得到效果较好的成像结果与道集提取图像。

单程波动方程偏移对比Kirchhoff偏移在一般情况下成像质量更高。1996年，Gray[22]得到相比于在复杂的模型中能获得较高成像质量的Kirchhoff偏移，傅里叶有限差分法偏移在复杂覆盖层以下目标带偏移剖面的成像精度更高的结论；2009年Ruttum et al.[23]就速度场对波动方程偏移的影响展开研究，得到波动方程偏移高度依赖于速度场空间密度，速度模型的精度直接关系到地震成像质量的结论；2019年李胜强[24]在密度约束速度下的叠前深度偏移在深地震探测中的应用展开研究，得到适用于ZK01井的密度-速度转换关系，并与经典Gardner转换公式比较，得出合适的密度-速度拟合可以得到精度更高的地震成像结果的结论。

逆时偏移成像(RTM)近几年也成为关注焦点。2013年，Yang et al.[25]研究了速度对逆时偏移储层成像的影响，无论是逆时偏移成像还是波动方程深度偏移成像，为了满足储层成像精度(包括波形和水平属性)的要求，速度误差都不应超过1%；2014年， Luo et al.[26]对逆时偏移Walkaway-VSP采集速度精度的影响进行了研究，传统的Walkaway-VSP成像方法虽然只可以对水平层状成像，不能对复杂构造成像，但是Walkaway-VSP对于逆冲推覆体成像精度较高；2017年，张思萌等[27]对逆时偏移在Marmousi模型中的双向照明波场分离成像条件进行了研究，在优化了互相关条件之后，浅层照明效果明显提升，但受速度场的影响，浅层部分噪音无法全部去除。

由以上的阐述可知，核心参数的选取对成像精度与成像效率有很大的影响，同样的，速度模型光滑对叠前深度偏移的成像质量有重要的影响。但是，目前的相关研究很少集中高斯束偏移这个方面。近期仅有2015年，袁茂林等[28]就高斯束核心参数对高斯束偏移的核心参数对高斯束偏移成像质量与效率的影响进行讨论；2016年韩建光[29]对模型进行适当光滑处理明显改善了高斯束成像效果的报道。事实上，参数选取与速度模型光滑问题在高斯偏移中是非常重要的一个问题。

鉴于此，本文对这两个问题展开研究，具体研究不同核心参数的优化选取以及不同光滑次数和光滑方式对Marmousi模型高斯束偏移成像质量的影响，重点研究影响射线路径、走时的核心参数和速度模型整体光滑和分层光滑对高斯束偏移成像的影响。

1 高斯束偏移方法

1.1 基本理论

高斯束的理论推导：在二维标量介质中,波场满足下述标量波动方程：

(1)

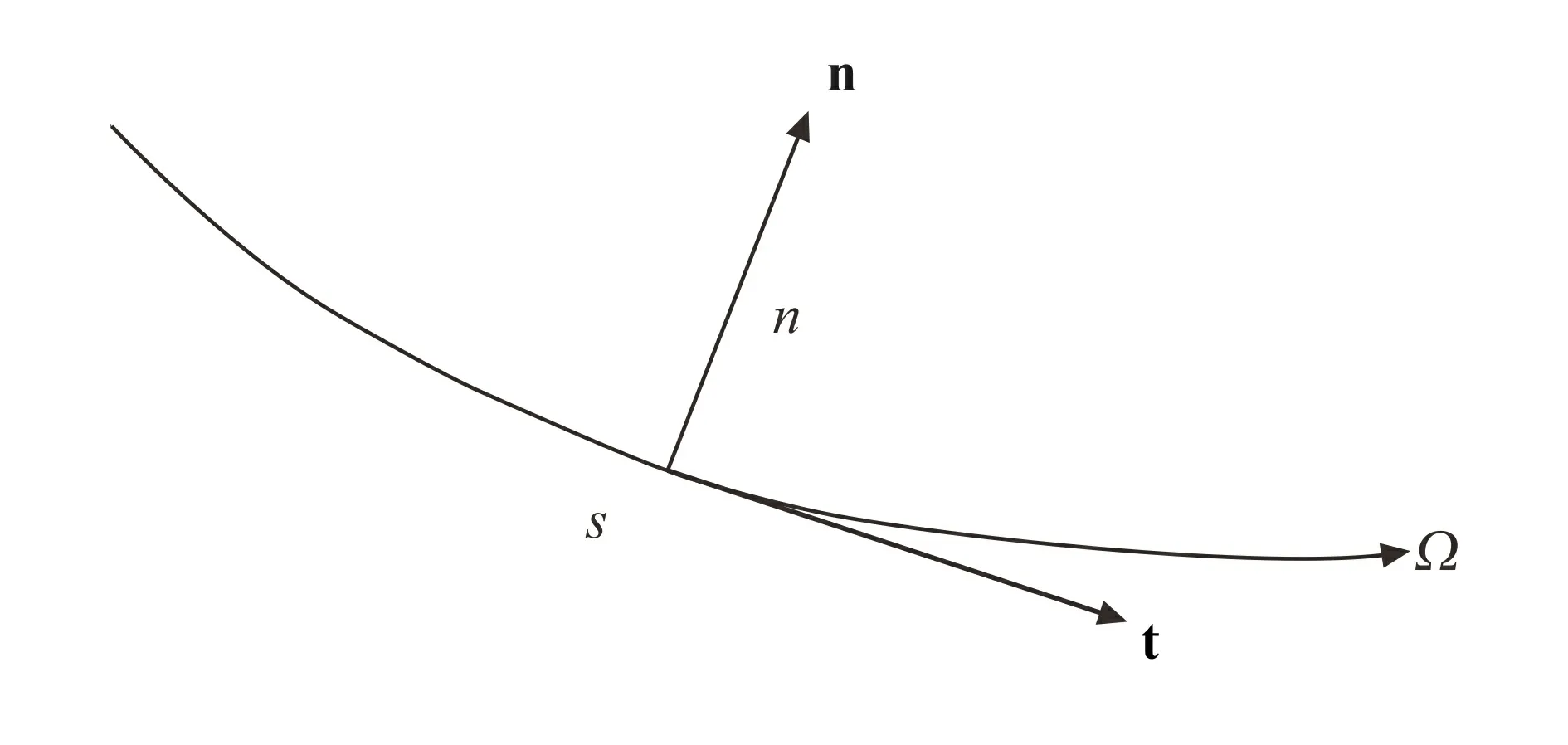
图1 二维射线中心坐标系Fig.1 Two dimensional ray center coordinate system

在图1的射线中心坐标系中，可以表示波动方程：

(2)

(3)

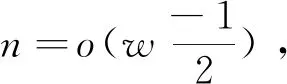
(4)

将式(3)、(4)代入式(2)，得：

(5)

式中：U=U(s,v,w)，若只考虑式(5)中关于ω的高阶项，可得：

(6)

式中：U=U(s,v)为U=U(s,v,w)的渐近级数的首阶项。然后通过以下代换：

(7)

将上式(7)其代入式(6)中，得到最终的抛物波动方程：

(8)

式(8)的一个特解可以写为：

(9)

A(s)，M(s)为未知的复值函数。将式(9)代入(8)，得：

(10)

以及：

(11)

式(10)为Riccati型一阶非线性微分方程，可以通过如下变换：

(12)

式中：P和Q为动力学射线追踪参数。式(10)可以代换为以下的线性微分方程组：

(13)

(14)

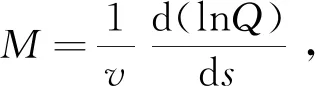
(15)

式中：Ψ为复常数。联立式(3)、(7)、(9)、(12)、(15)就可以得到中心射线Ω邻域的波动方程高频渐进解：

(16)

P(s0)=aP1(s0)+ibP2(s0)

(17)

Q(s0)=aQ1(s0)+ibQ2(s0)

(18)

式(17)、(18)中：a和b为实常数且a×b>0；P1(s0)≠0，Q1(s0)=0为动力学射线追踪方程(13)、(14)的点源解的初始值，P2(s0)=0，Q2(s0)≠0为方程(13)、(14)的线源解的初始值。

高斯束的具体数值求解首先要根据高斯束的初始位置和初始方向,利用如下运动学射线追踪方程组来求取中心射线的路径和走时：

(19)

(20)

式(19)、(20)中：Pi(S)代表射线慢度矢量的水平和垂直分量；xi(s)和τ分别代表直角坐标中的射线坐标和沿射线的走时。

射线路径和走时计算完成后，利用如下的动力学射线追踪方程组来求取中心射线的动力学参量：

(21)

(22)

(23)

根据由式(21)、(22)得出的式(23)，θ代表射线的传播方向同正轴的夹角，经典的四阶Runger-Kutta法可以用来求解如上的偏微分方程，由运动学和动力学射线追踪方程组可知速度变化，是速度模型光滑理论的基础。

最后,由射线追踪所求得的中心射线上的有效信息,根据式(16)求取中心射线附近振幅大于中心射线振幅范围的波场。

高斯束的基本性质：在这里首先忽略式(16)中的exp(-iwt)并分离P(s)/Q(s)的实部和虚部,就可以得到具有更为明显的物理意义的高斯束频率域表达式：

高斯束的初始宽度和波前曲率由式(16)中动力学射线追踪方程的Hill给定初始值确定，其中的点源和线源初始条件为式(25)、(26)[30]：

Q1(s0)=1，P1(s0)=0

(25)

Q2(s0)=0，P2(s0)=1

(26)

系数和为式(27)：

(27)

式中：wr为参考频率；w0为初始宽度。最终可以得到式(28)：

(28)

由上式可知，P(s0)/Q(s0)为一个纯虚数，此时，说明高斯束波前在其初始位置S0处为平面[31]。

1.2 叠前偏移

炮域高斯束偏移的基本原理如图2所示，具体流程为，首先在对应单炮的接收排列上确定束中心的位置，给出根据波场双向延拓积分的叠前成像公式：

(29)

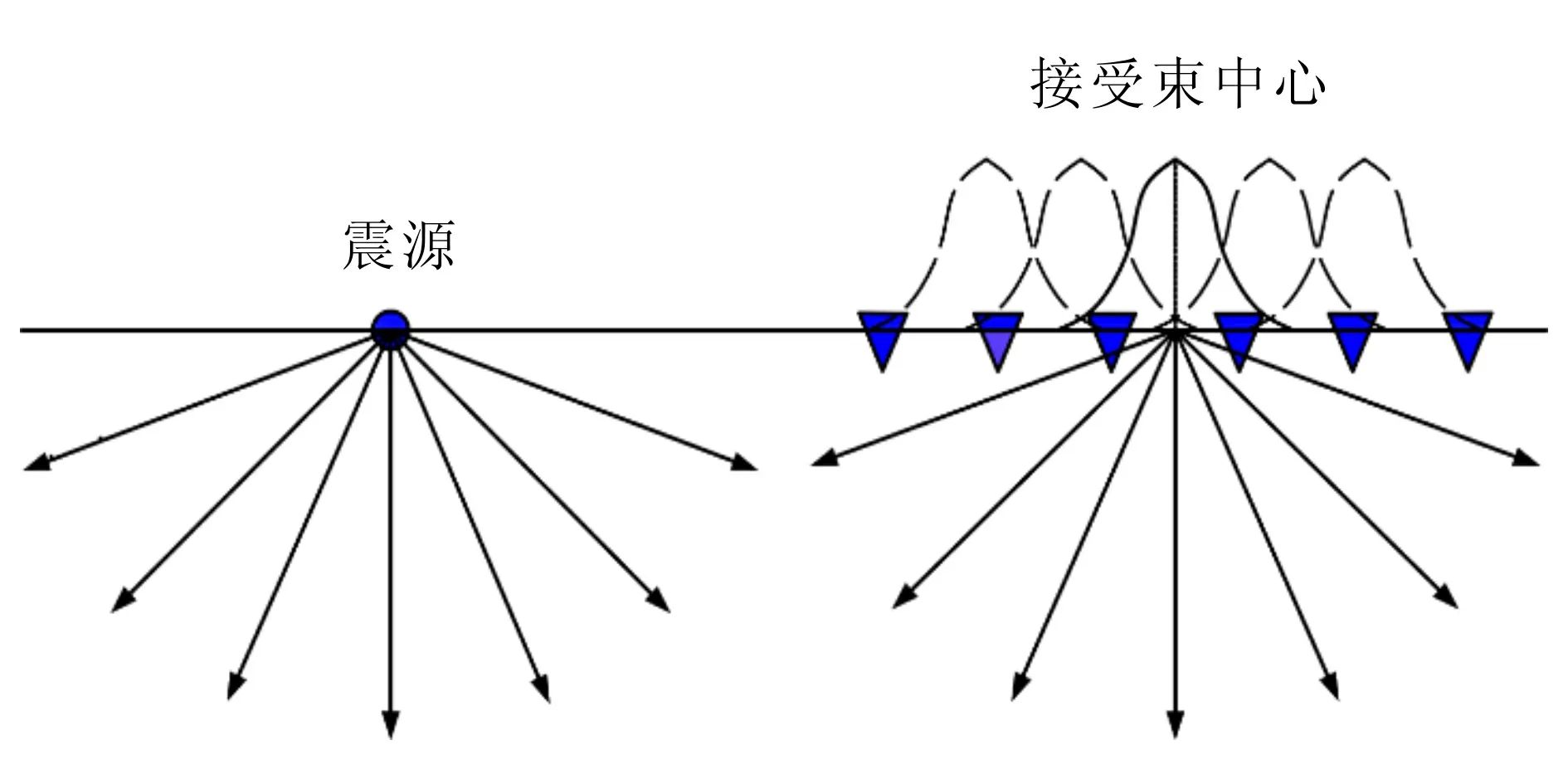
图2 炮域高斯束偏移的基本原理Fig.2 Basic principle of Gaussian beam migration in shot field

将式(29)中的格林函数用高斯束积分表示可得下式：

(30)

接着在对应单炮的接收排列上确定束中心的位置，得到束中心位置Lr：

(31)

联立以上各式，可得共炮点道集偏移公式：

(32)

1.3 实现流程

式(32)偏移成像公式的核心部分：

(33)

计算流程为：①对于每个束中心位置，孔径内成像点根据高斯束的走时和振幅进行倾斜叠加道成像；②将上述每个中心点射线参数成像点成的像加窗局部倾斜叠加投影到地震道局限的位置处。

此算法可对所有的波至进行成像，虽然精确度很高但是计算效率低，因为对单个成像数据体，有nb个束中心位置，nps个震源高斯束，npr个接收点高斯束，计算量为nb×nps×npr×局部孔径的成像运算。

本文的高斯束偏移实现流程采用Hill[32]提出的一种高效率高斯束偏移方法，式(33)因为是一个多维高频复值震荡积分，所以可以用最速下降法将积分降维提高计算效率，实现流程是用中心点和偏移距域射线参数代换积分变量中的震源和接收点射线参数，得到式(34)：

(34)

其中：

Ch(x,Lr,pm,w)

=∬dphxdphyA(x,pm,ph)exp[-iwT*(x,pm,ph)]

(35)

式中：A(x,pm,pn)是震源和接收点高斯束的振幅乘积；T(x,pm,ph)是复值走时之和，虽然渐进解由Hill[33]提出，但是没有精确求取振幅项：

(36)

式中：T0是虚值走时最小时高斯束走时之和；A0是震源高斯束同接收点高斯束之和。将式(36)代入式(35)，得式(37)：

(37)

计算流程为：①对于每个束中心位置，扫描每个粗网格点并确定使虚值走时最小的偏移距射线参数；②对于每个束中心位置，孔径内成像点根据高斯束的走时和振幅进行倾斜叠加道成像；③将上述每个中心点射线参数成像点成的像加窗局部倾斜叠加投影到地震道局限的位置处。

此高效算法计算效率较高，计算量是nb×(nps×npr-1)×(局部孔径的成像运算+粗网格上最小虚值走时的搜索)。

2 高斯束偏移核心参数的影响

从高斯束偏移理论和公式中可以看出，在高斯束偏移中存在几个重要核心参数，笔者研究了包括最大出射角度、傍轴射线数量、高斯束半宽、窗的半宽及束中心间隔。这些参数的选取直接影响到偏移成像质量以及计算效率。因此，对这些参数进行了系统的分析和成像测试。

按图3中所示的红色与绿色矩形区域分别是Marmousi模型的浅层断层构造与深层的背斜构造，对浅层与深层的成像效果进行放大对比，讨论各个核心参数对成像效果的影响，根据各参数的成像调试结果，给出了优化选取准则。

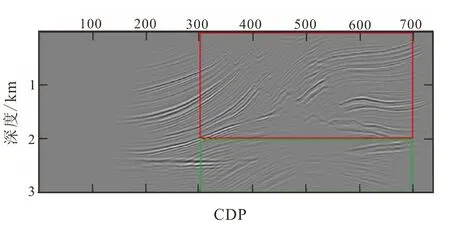
红色矩形圈定部分为断层，绿色矩形圈定部分为背斜。图3 高斯束偏移成像图的主要对比部分Fig.3 Main contrast of Gaussian beam migration image

2.1 最大出射角度

地表处出射的高斯束射线受到其最大出射角度的限制，最大出射角度限制了浅部数据的读取，本文用30°、40°、50°和90° 4种不同的最大出射角对Marmousi模型进行成像。

图4 最大出射角度分别为30°(a)、40°(b)、50°(c)、90°(d)的成像结果Fig.4 Imaging results with maximum exit angles of 30° (a) , 40° (b) , 50° (c) and 90° (d)

如图4～6所示，对于最大出射角为30°(图4a、5a、6a)、最大出射角为40°(图4c、5c、6c)、最大出射角为50°(图4b、5b、6b)和最大出射角为90°(图4d、5d、6d) 偏移成像的浅层构造部分内容逐渐丰富，相比较而言后者的浅部构造更加清晰；相对而言，其深部的背斜构造逐渐失真，在最大初射角度为90°时，失真更加严重，当最大出射角度取50°时，浅部构造清晰且深层背斜构造清晰。

图5 最大出射角度分别为30°(a)、40°(b)、50°(c)、90°(d)的浅层断层构造成像结果Fig.5 Shallow fault structures imaging results with maximum exit angles of 30° (a) , 40° (b) , 50° (c) and 90° (d)

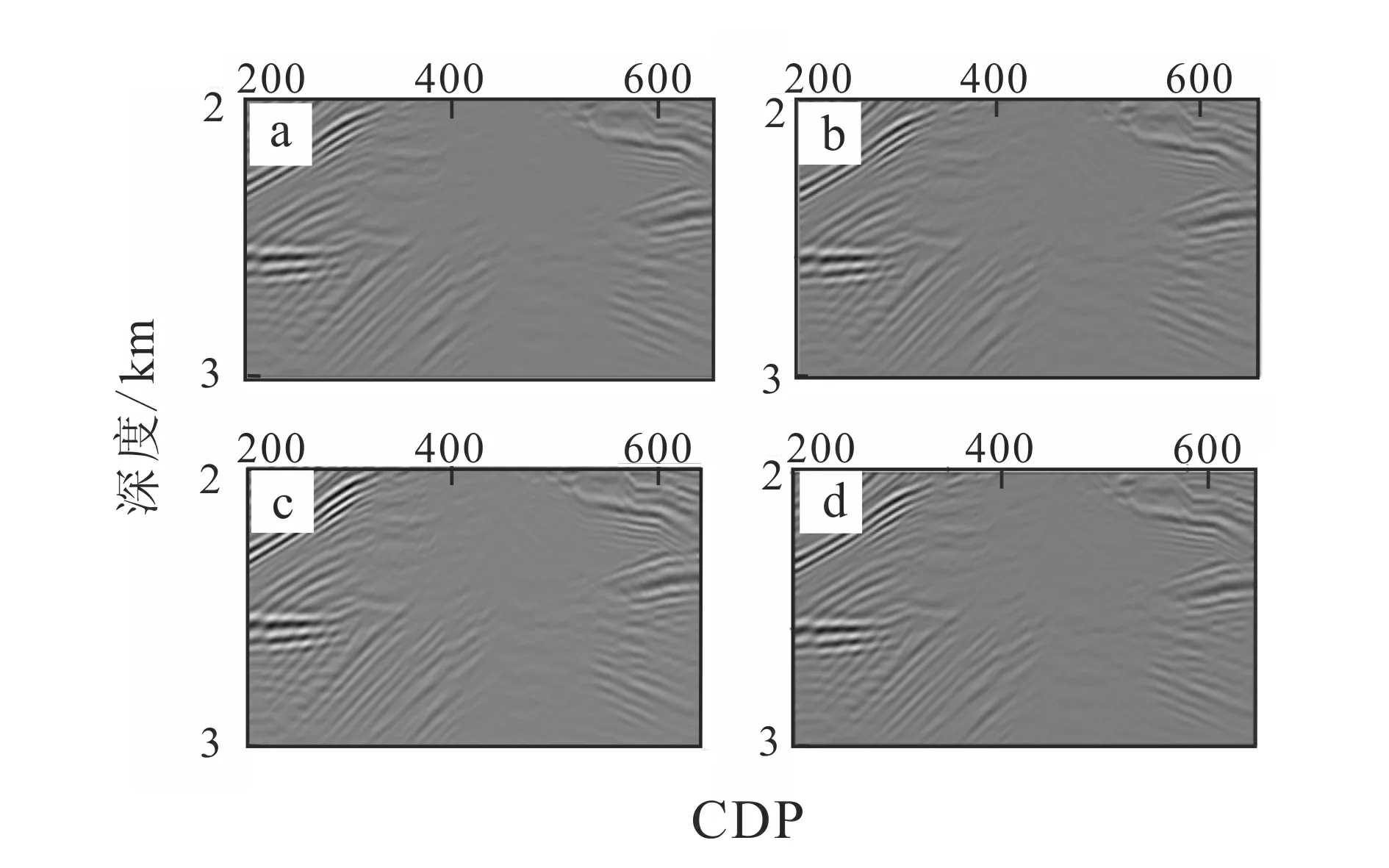
图6 最大出射角度分别为30°(a)、40°(b)、50°(c)、90°(d)的深层背斜构造成像结果Fig.6 Deep anticline structures imaging results with maximum exit angles of 30° (a) , 40° (b) , 50° (c) and 90° (d)

2.2 傍轴射线数量

傍轴射线数量的多少不仅影响着成像精度，同样也影响偏移程序的成像效率，射线数量多会使成像精度变高，却降低成像效率，反之亦然，本文调节参数为30、40、50、60。

从表1中可以看到，成像结果的质量相差不大，而在ψ=30°时，其成像效率较之ψ=60°时相差一倍，而ψ<30°时，由于射线覆盖不完全，无法输出成像结果。如图7～9所示，对于傍轴射线数量为30(图7a、8a、9a)、傍轴射线数量为40(图7b、8b、9b)、傍轴射线数量为50(图7c、8c、9c)和傍轴射线数量为60(图7d、8d、9d)偏移成像的结果变化不大，然而，相比较而言后者的计算效率更加快捷有效，取ψ=30，40，50，60的计算效率。如表1所示,相对而言，计算效率提高的同时，浅层断层部位的成像结果明显变差。

表1 傍轴射线数对运算时间的影响

图7 傍轴射线数量分别为30(a)、40(b)、50(c)、60(d)的成像结果Fig.7 Imaging results with paraxial ray numbers of 30 (a), 40 (b), 50 (c) and 60 (d)

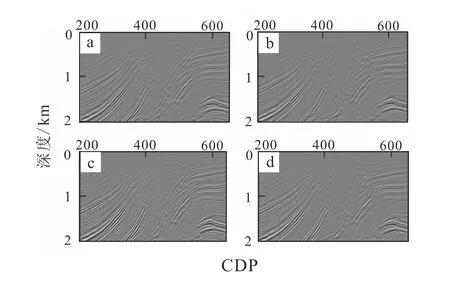
图8 傍轴射线数量分别为30(a)、40(b)、50(c)、60(d)的浅层断层构造成像结果Fig.8 Shallow fault structures imaging results with paraxial ray numbers of 30 (a), 40 (b), 50 (c) and 60 (d)

图9 傍轴射线数量分别为30(a)、40(b)、50(c)、60(d)的深层背斜构造成像结果Fig.9 Deep anticline structures imaging results with paraxial ray numbers of 30 (a), 40 (b), 50 (c) and 60 (d)

2.3 高斯窗的半宽

选取不同的窗半宽进行成像测试，并分析了不同窗半宽对高斯束偏移成像质量以及计算效率的影响，由于窗半宽与束半宽为相关参数，故于固定束半宽(497.6 m)下研究窗半宽对成像的影响。

如图10显示了高斯窗半宽为248.8 m(图10a)、746.4 m(图10b)和1 244 m(图10c)时的成像结果。

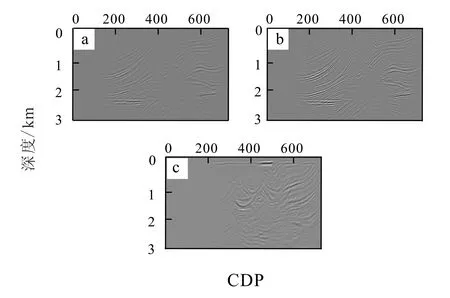
图10 不同窗半宽分别为248.8 m(a)、746.4 m(b)和1 244 m(c)成像结果Fig.10 Imaging results with different windows half widths of 248.8 m (a), 746.4 m (b) and 1 244 m (b)

高斯窗半宽在248.8 m时，由于高斯窗半宽过小，无法完全覆盖所有成像区域，浅层地层成像失真较为严重；高斯窗半宽在1 244 m时，由于高斯窗半宽过大，成像区域的成像结果重叠，成像效果失真极其严重；高斯窗半宽在746.4 m时，由于高斯窗半宽合适，成像区域的成像结果清晰，浅层与深层成像效果较好。

2.4 高斯束的半宽

同样，由于窗半宽与束半宽为相关参数，故于固定窗半宽(746.4 m)下研究束半宽对成像的影响。地表处出射的高斯束射线的束宽越窄，地震波场越精确。如果初始束宽过小(取99.52 m时)，或者过大(取497.6 m时)，会降低地震波场的精度。

如图11～13所示，高斯束半宽在99.52 m时，由于高斯束半宽过小，浅层断层地层成像失真严重，成像精度非常低；深层背斜构造的成像失真情况不明显。高斯束半宽在497.6 m时，由于高斯束半宽较小，浅层断层地层成像失真比较严重，成像精度变低；深层背斜构造的成像失真较为严重。高斯束半宽在248.8 m时，由于高斯束半宽合适，成像区域的成像结果清晰，浅层与深层成像效果较好。高斯束半宽过大(>497.6 m)时，由于半宽过大，导致无法成像。

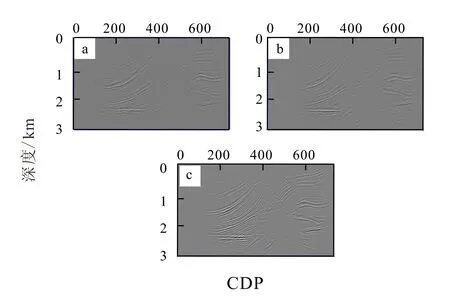
图11 高斯束半宽为99.52 m(a)、248.8 m(b)和497.6 m(c)成像结果Fig.11 Imaging results with Gaussian beam half widths of 99.52 m (a), 248.8 m (b) and 497.6 m (c)

图12 高斯束半宽分别为99.52 m(a)、248.8 m(b)和497.6 m(c)的浅层断层构造成像结果Fig.12 Shallow fault structures imaging results with Gaussian beam half widths are 99.52 m(a), 248.8 m(b) and 497.6 m(c)

图13 高斯束半宽分别为99.52 m(a)、248.8 m(b)和497.6 m(c)的深层背斜构造成像结果Fig.13 Deep anticline structures imaging results with Gaussian beam half widths of 99.52 m (a), 248.8 m (b) and 497.6 m (c)

2.5 高斯束中心间隔

束中心间隔的大小不仅影响着成像精度，同样也影响偏移程序的成像效率，束中心间隔的减小会使射线稠密，成像精度变高，却降低成像效率，反之亦然，本文调节束中心间隔为250 m、270 m、300 m和500 m。

从表2中可以看到，其他条件固定的情况下，在束中心间隔L=250 m时，其成像效率较之L=500 m时相差近一倍。

表2 束中心间隔对运算时间的影响

如图14～16所示，在浅层断层构造的成像对比中，对于束中心间隔为250 m(图15a)，断层构造成像最为清晰，而计算效率较低，对于束中心间隔为270 m(图15b)和300 m(图15c)的浅层成像结果的精度相近，计算效率上L=300 m的成像效率更高；在深层背斜构造的成像对比中，对于束中心间隔为250 m、270 m、300 m和500 m(图16)的偏移成像的结果变化不大，然而，相比较而言后者的计算效率更加快捷有效；束中心间隔为500 m(图15d)的浅层成像结果明显失真，束中心间隔L=250 m、270 m、300 m、500 m的计算效率如表2所示；即计算效率提高的同时，浅层断层部位的成像结果明显变差。可以观察到在束中心间隔取L=300 m时可以在确保成像结果的精度的同时，最大效率对地下进行成像。

图14 束中心间隔为250 m(a)、270 m(b)、300 m(c)、500 m(d)的成像结果Fig.14 Imaging results with beam center spacing of 250 m (a), 270 m (b), 300 m (c) and 500 m (d)

图15 束中心间隔为250 m(a)、270 m(b)、300 m(c)、500 m(d)的浅层断层构造成像结果Fig.15 Shallow fault structures imaging results with center spacing of 250 m (a), 270 m (b), 300 m (c) and 500 m (d)

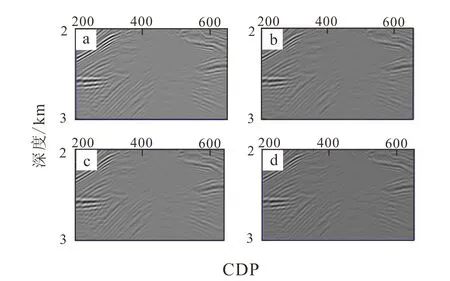
图16 束中心间隔为250 m(a)、270 m(b)、300 m(c)、500 m(d)的深层背斜构造成像结果Fig.16 Deep anticline structure imaging results with center spacing of 250 m (a), 270 m (b), 300 m (c) and 500 m (d)

高斯束偏移核心参数经过优化后得到高斯束偏移最优参数组合，最大出射角度取用50°，傍轴射线数取用30，高斯窗半宽取用746.4 m，高斯束半宽取用497.6 m，束中心间隔取用300 m时，可以同时确保高斯束偏移的成像精度与成像效率(图17)。

图17 最优参数组合的高斯束偏移成像结果Fig.17 Gaussian beam migration imaging results with optimal parameter combination

对高斯束偏移中一系列参数的选取进行了讨论，并给出了优化的选取准则，通过数值试验对Marmousi模型的成像效果进行了对比并分析高斯束偏移中重要的参数设定。本文在数值测试的过程中，均使用了最大成像角度为130°的控制原则，该角度一般情况下可以保证对有效反射能量的成像，并且排除折射波造成的低频成像噪声。

3 速度模型光滑的影响

3.1 理论基础

运动学和动力学射线追踪方程组(19)、(20)和(21)、(22)的求解可以用射线追踪法，得到射线路径、振幅和走时。式(19)、 (20)和(21)、(22)中的i=1，2，3;Q，P，V代表2×2的矩阵，v代表速度，pi代表慢度分量，xi代表位置坐标分量。

每个分量的定义为：

式中：γI(I=1,2)代表沿着每条射线的射线参数，qI(I=1,2)代表中心射线坐标。从运动学和动力学射线追踪方程组(19)、(20)和(21)、(22)可知速度模型必须具有二阶连续的导数。但在实际应用中，速度模型设置比较复杂，每一个速度都以网格的形式定义在节点上，具有不连续的速度突变间断面和强烈的速度梯度。所以为了满足射线理论的高频近似，需要对模型进行光滑处理减小速度的变化。

3.2 偏移速度模型光滑处理研究

射线理论要求模型满足相对光滑的条件，速度模型的光滑是为了满足应用射线追踪的高频条件。本文采用卷积类平滑算子：

(38)

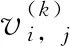
3.3 模型整体光滑对偏移成像的影响

利用式(38)的卷积类平滑算子对速度模型进行光滑处理，设平滑因子w=0.5。图18为横向纵向交替光滑20次、30次、40次、120次、500次和1 000次的Marmousi模型及高斯束偏移成像图。

如图18所示，经过光滑处理后，易看出随着光滑次数的增加，速度模型的特征逐渐失真，尤其是在光滑了1 000之后，Marmousi模型的构造特征严重失真。如图19所示，光滑20次、光滑50次和光滑100次的偏移成像质量较好，从整体上不易看出区别，但可看出光滑120次及以后偏移图像质量明显下降，浅层和深层构造逐渐失真，而光滑1 000次后整个偏移成像结果已经严重扭曲和出现了明显错误。为了更直观的看出Marmousi模型光滑对高斯束偏移成像的影响，放大对比分析Marmousi模型光滑20次、30次、40次、120次、500次与1 000次的高斯束偏移成像图。

高斯束偏移成像结果与原速度模型相比，吻合得较好，能清晰得看出3个断层。如图20所示，虽然光滑20次(图20b)、光滑50次(图20c)和光滑100次(图20d)的Marmousi模型偏移成像结果差别不是很明显，但是相比于光滑20次和30次，光滑100次左侧断层和右侧断层下部偏移成像质量更高。如图20e所示，当光滑120次后，能清楚地看到断层界限部分失真，最右边断层的底部更为明显。如图20f所示，当光滑500次后，最左边和中间的断层界限基本已经消失，最右边的断层上部也只能观察到细微界限。如图20g所示，当光滑了1 000次之后，断层界限已消失，偏移图像严重失真。由上述内容知，速度模型的整体光滑处理对高斯束偏移的成像中的浅层高陡构造影响有限，过度光滑会造成成像质量严重失真，适当光滑可以提高偏移成像质量，在光滑次数100次以内有较好的成像质量。

(a)光滑20次；(b)光滑50次；(c)光滑100次；(d)光滑120次；(e)光滑500次；(f)光滑1 000次。图19 Marmousi模型高斯束偏移成像图Fig.19 Marmousi models of Gaussian beam migration image

(a)光滑20次；(b)光滑20次；(c)光滑50次；(d)光滑100次；(e)光滑120次；(f)光滑500次；(g)光滑1 000次。图20 Marmousi模型及其高斯束偏移成像红色矩形圈定部分放大图Fig.20 Marmousi models of Gaussian beam migration imaging with red rectangle enlargement

对绿色矩形圈定部分进行对比分析如图21a和21b所示，高斯束偏移成像结果与原速度模型相比，吻合得较好，能清晰地看出背斜构造。如图21b、21c和21d所示，虽然光滑20次、光滑50次和光滑100次的Marmousi模型偏移成像结果差别不是很明显，但是相比于光滑20次和40次，光滑50次偏移成像质量更高，背斜构造更清晰。如图21e所示，当光滑120次后，能清楚地看到背斜构造的中上部分失真。如图21f和21g所示，当光滑500次和1 000次后，背斜构造已经严重失真，尤其是底部特征。由上述内容知，相比于对浅层高陡构造的影响，速度模型的整体光滑处理对高斯束偏移的成像中的深部底层构造影响更大，过度光滑会造成成像质量严重失真，适当光滑可以提高偏移成像质量。

(a)光滑20次；(b)光滑20次；(c)光滑50次；(d)光滑100次；(e)光滑120次；(f)光滑500次；(g)光滑1 000次。图21 Marmousi模型及其高斯束偏移成像绿色矩形圈定部分放大图Fig.21 Marmousi models of Gaussian beam migration imaging with green rectangle enlargement

从上述对比分析中可以得出以下结论：速度模型的整体光滑处理对高斯束偏移的成像中的浅层高陡构造影响有限，但对深部底层构造影响较大，过度光滑会造成成像质量严重失真，适当光滑可以提高偏移成像质量。因此，在实际工作当中为了确保高斯束成像质量，整体光滑次数不要超过100次。

3.4 模型分层光滑对偏移成像的影响

接下来进行模型分层光滑对偏移影响的研究，其中着重研究速度模型模型浅地层光滑对高斯束偏移质量的影响，将Marmousi速度模型纵方向不同深度进行光滑，地表至地下0.4 km、地下1.2～1.6 km、地下2.4～2.8 km横纵交替光滑1 000次，在地表至地下0.2 km速度均赋值1 500 m/s，并在地下0.16～0.24 km横纵交替光滑100次。

如图22所示，模型分层光滑处理效果明显，光滑部分与相邻部分相比严重失真。接着将模型光滑处理后的高斯束偏移成像图的浅层高陡构造和深层背斜构造放大进行对比分析。

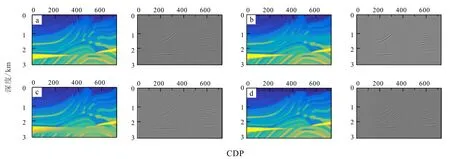
(a)地表至地下0.4 km光滑1 000次；(b)地下1.2～1.6 km光滑1 000次；(c)地下2.4～2.8 km光滑1 000次；(d)地表至地下0.2 km赋值速度1 500 m/s并在地下0.16～0.24 km光滑100次。图22 光滑处理的Marmousi模型(左)和其高斯束偏移成像图(右)Fig.22 Marmousi models (left) and its Gaussian beam migration images (right) processed by smoothing

如图23所示，对于模型浅层光滑，地表至地下0.4 km光滑1 000次(图23a)和地表至地下0.2 km内速度赋值1 500 m/s，并在地下0.16～0.24 km光滑100次(图23d)偏移成像的浅层高陡构造严重失真；对于模型中层光滑，地下1.2～1.6 km光滑1 000次(图23b)偏移成像的浅层高陡构造部分失真，中间断层底部尤为明显；对于模型深层光滑，地下2.4～2.8 km光滑1 000次(图23c)偏移成像的浅层高陡构造较清晰，偏移成像质量较高。

(a)地表至地下0.4 km光滑1 000次；(b)地下1.2～1.6 km光滑1 000次；(c)地下2.4～2.8 km光滑1 000次；(d)地表至地下0.2 km内赋值速度1 500 m/s并在地下0.16～0.24 km内光滑100次。图23 Marmousi模型高斯束偏移成像红色矩形圈定部分放大图Fig.23 Marmousi models of Gaussian beam migration imaging with red rectangle enlargement

如图24所示，对于模型浅层光滑，地表至地下0.4 km光滑1 000次(图24a)和地表至地下0.2 km内速度赋值1 500 m/s，并在地下0.16～0.24 km光滑100次(图24d)偏移成像的深层背斜构造部分失真，相比较而言后者失真要更严重；对于模型中层光滑，地下1.2～1.6 km光滑1 000次(图24b)偏移成像的深层背斜构造严重失真；对于模型深层光滑，地下2.4～2.8 km光滑1 000次(图24c)偏移成像的深层背斜构造较清晰，偏移成像质量较高。

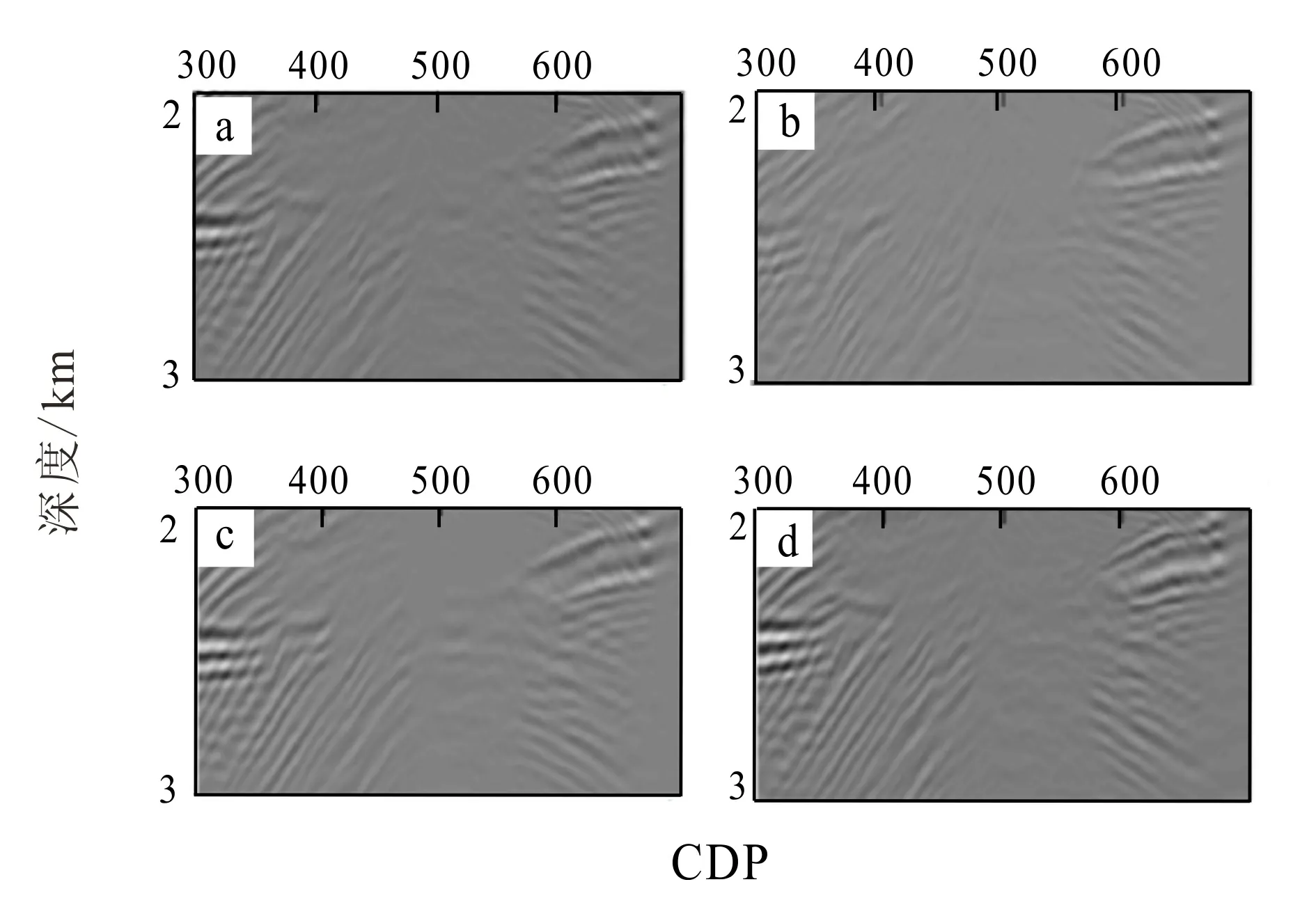
(a)地表至地下0.4 km光滑1 000次；(b)地下1.2～1.6 km光滑1 000次；(c)地下2.4～2.8 km光滑1 000次；(d)地表至地下0.2 km赋值速度1 500 m/s并在地下0.16～0.24 km光滑100次。图24 Marmousi模型高斯束偏移成像绿色矩形圈定部分放大图Fig.24 Marmousi models of Gaussian beam migration imaging with green rectangle enlargement

从上述对比分析中可以得出以下结论：速度模型浅层光滑对浅层高陡构造和深层背斜构造影响都较大，即高斯束偏移对近地表速度模型光滑相对敏感。速度模型浅层光滑在深层背斜构造中部失真，在两侧影响较小，该现象说明速度模型浅层光滑对高斯束偏移成像在深部横向影响较大，纵向影响较小。近地表速度光滑程度很大时，高斯束偏移成像质量较差，该现象说明高斯束偏移对近地表速度模型的精度要求很高，即在进行复杂近地表偏移成像时，近地表速度建模尤为重要。