基于奇异谱分析的SPBO-ANFIS月径流组合预测模型

张亚杰，崔东文

(1.云南省玉溪市易门县水利局，云南 玉溪 651100；2.云南省文山州水务局，云南 文山 663000)

中长期径流预报的准确性和预见性对于区域水资源规划与管理具有重要意义。由于径流受气候变化、地环境和人类活动的多重影响，呈现出较强的非线性、非平稳性和多尺度等特征，使得预测难度大大增加，传统单一模型或方法难以获得满意的预测效果[1-2]。研究表明，提高径流时间序列预测精度的关键在于原始序列的有效分解和预测器的合理选取。时序数据分解方法有经验模态分解(EMD)、总体经验模态分解(EEMD)、小波分解(WD)、奇异谱分析(SSA)、小波包分解(WPD)等，均在时间序列预测研究中得到广泛应用；预测器有自回归滑动平均模型[3]、人工神经网络模型[4-5]、支持向量机(SVM)[6]、相关向量机(RVM)[7]、LSTM神经网络[8-9]等。

奇异谱分析(Singular Spectrum Analysis，SSA)是近年来兴起的一种研究非线性时间序列数据的有效方法，它根据所观测到的时间序列构造出轨迹矩阵，并对轨迹矩阵进行分解、重构，从而获得更具规律的子序列分量，目前已在月径流时间序列预报中得到应用[6]。月径流时间序列预测器主要有BP、SVM、LSTM等，BP神经网络存在设置参数多、易陷入局部最优等缺点；SVM模型存在对参数敏感、大容量样本预报中表现不佳等不足；LSTM模型预测性能较好，但存在内存资源消耗大、运行时间长等缺陷。本文预测器选用自适应神经模糊推理系统(Adaptive Network based Fuzzy Inference System，ANFIS)。ANFIS具有较强的学习能力和表达能力，但其条件参数、结论参数的选取是制约ANFIS性能提高的关键因素，采用一种新型群体智能算法——学生心理学优化(Student Psychology Based Optimization，SPBO)算法优化ANFIS条件参数、结论参数，以期提高ANFIS预测器性能和智能化水平。基于此，为有效提高径流时间序列预测精度，克服单一模型的不足，基于SSA方法、SPBO算法、ANFIS系统，提出SSA-SPBO-ANFIS月径流时间序列组合预测模型。主要内容包括：①以云南省某水文站1960年1月至2012年12月共636个月月径流预测为例，利用SSA对原始月径流时间序列数据特征进行充分提取，将原序列分解为若干独立子序列；②简要介绍SPBO算法，对验证SPBO算法寻优能力，选取8个典型单峰和多峰测试函数在不同维度条件下对SPBO算法的寻优能力进行仿真测试，并与当前寻优效果较好的教学优化(LTBO)算法的寻优结果进行比较；③选取自适应神经模糊推理系统(ANFIS)作为月径流时间序列预测模型，利用SPBO算法优化ANFIS条件参数和结论参数，建立SSA-SPBO-ANFIS组合模型对分解后的各子序列进行预测，叠加后作为最终月径流预测结果，并构建基于集合经验模态分解(EEMD)的EEMD-SPBO-ANFIS模型和未经分解的SPBO-ANFIS模型作对比分析模型。

1 SSA-SPBO-ANFIS预测模型

1.1 奇异谱分析(SSA)

SSA是一种非线性时序数据处理方法，对于研究周期振荡行为具有独到的优势，其原理基于时间序列的动力重构，是经验函数正交分解的一种特殊应用，能够有效地从包含噪声的有限尺度时间序列中提取特征信息。SSA包含分解与重构2个阶段[10-13]。

a)分解。选取窗口长度L构造轨迹矩阵X如下：

(1)

式中M——时间序列长度；L——窗口长度，即嵌入维数。

对矩阵X进行SVD分解：

(2)

式中λi——第i个特征值；Ui——与第i个特征值对应的特征向量；Vi——第i个主成分；d=rank(X)=max{i∶λi>0}。

(3)

式中 向量数量K=M-L+1；L*=min(L,K)；K*=max(L,K)。

1.2 学生心理学优化(SPBO)算法

1.2.1SPBO算法简述

学生心理学优化(SPBO)算法是Bikash Das等人基于班级学生通过努力提高学习成绩、争当优等生心理而提出的一种新型群体智能优化算法。该算法根据班级学生表现将学生分为最优学生、好学生、普通学生和尝试随机提高学生4类，通过模拟此4类学生提高学习成绩来达到求解优化问题的目的。SPBO算法基于以下假设：①学生成绩通过考试得分衡量，在考试中获得最高分数的学生被认为是班级最优学生；②班级中其他学生会通过努力来提高考试成绩，并成为班级最优学生，考试成绩提高途径因学生不同而各异；③要成为班级最优学生，需要在所学科目上付出更多努力，任何一个学生对任何一门学科的努力都取决于学生的能力、效率以及对该学科的兴趣；④除优秀学生外，其余3类学生(好学生、普通学生和尝试随机提高学生)的学科选择视为一个随机过程[14]。

SPBO算法数学描述简述如下[14]。

a)最优学生。最优学生始终通过努力获得全班最高分来维持自己的位置。为获得最高分并维持自己的位置，最优学生需要对每个学科付出比其他学生更多的努力。最优学生考试成绩描述如下：

Xbestnew=Xbest+(-1)k×rand×(Xbest-Xj)

(4)

式中Xbestnew——当前最优学生某一学科考试成绩；Xbest——最优学生某一学科考试成绩；Xj——第j名学生某一学科考试成绩；rand——[0,1]范围内随机数；k——随机选择为1或2的参数。

b)好学生。如果学生对某学科感兴趣，那么她/他会在该学科上付出更多努力，从而使她/他的整体成绩得到提高。这类学生的选择是一个随机过程，为通过在考试中获得最高分而成为最优学生，该类学生会尝试做出与最优学生相似或更多的努力。好学生考试成绩描述如下：

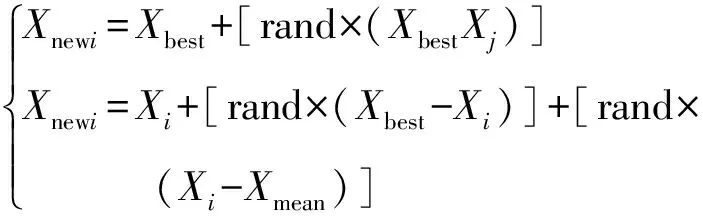
(5)

式中Xnewi——当前随机选择学生某一学科考试成绩；Xi——第i名学生某一学科考试成绩；Xmean——某一学科平均考试成绩；其他参数意义同上。

c)普通学生。学生努力程度取决于学生对所学科目的兴趣，如果该类学生对某学科不太感兴趣，那么该类学生将为该科目付出平均努力。在平均努力学习该科目的同时，该类学生将尝试在其他学科上付出更多努力来提高他们的整体成绩。根据学生的不同心理，普通学生的选拔也是一个随机过程。普通学生考试成绩描述如下：

Xnewi=Xi+[rand×(Xmean-Xi)]

(6)

d)尝试随机提高学生。除上述3类学生外，有些学生试图自己提高学习成绩。该类学生尝试随机对科目进行努力，以提高考试的整体成绩。该类学生考试成绩描述如下：

Xnewi=Xmin+[rand×(Xmax-Xmin)]

(7)

式中Xmax、Xmin——某一学科考试最高分、最低分。

1.2.2SPBO算法仿真验证

选取Sphere等8个典型测试函数在不同维度条件下对SPBO算法进行仿真验证，并与当前具有较好寻优效果的TLBO算法的仿真结果进行比较，见表1。设置SPBO、TLBO算法最大迭代次数T=500，群体规模N=50；其中TLBO算法参数TF为1～10之间随机整数。

表1 函数优化对比结果

对于单峰函数，SPBO算法寻优精度较TLBO算法提高20个数量级以上。对于多峰函数Griewank，SPBO算法在低维(10维)条件寻优效果远优于TLBO算法，其他维度条件下与TLBO算法相同。对于Rastrigin函数，SPBO算法在不同维度条件下20次寻优均获得理论最优值0，具有理想的寻优效果。对于Penalized函数，SPBO算法在不同维度条件下寻优精度均在4.71E-32以上，在低维(10维)条件下，SPBO算法寻优精度略优于TLBO算法；在高维条件下，SPBO算法寻优精度远优于TLBO算法。对于多峰函数Levy，SPBO算法在不同维度条件下寻优精度均为1.50E-32，在低维(10维)条件下，SPBO算法寻优精度略优于TLBO算法；在高维条件下，SPBO算法寻优精度远优于TLBO算法。

可见，在上述条件下，SPBO算法寻优效果优于TLBO算法，具有较好的寻优性能。

1.3 自适应神经模糊推理系统(ANFIS)

ANFIS兼顾了神经网络学习机制和模糊系统语言推理能力的优点，已在多个领域得到了成功应用。ANFIS结构表示见式(8)[15-19]：

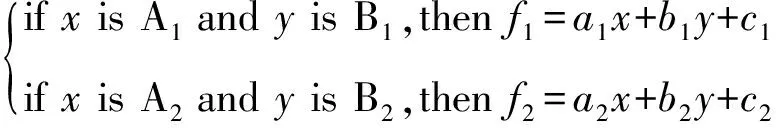
(8)

式中x、y——输入；A1、B1、A2、B2——模糊语言；a1、b1、c1——规则1的结论参数；a2、b2、c2——规则2的结论参数；f1、f2——规则输出。

ANFIS推理系统通常由5层数学模型组成，在给定条件参数后，ANFIS输出可以表示成结论参数的线性组合：

(9)

1.4 SSA-SPBO-ANFIS建模流程

步骤一利用SSA将原非平稳月径流时间序列分解为若干独立子序列IMF；通过偏自相关函数法(PAFM)、自相关函数法(AFM)综合确定各IMF输入向量，合理划分训练样本和预测样本。流程见图1。

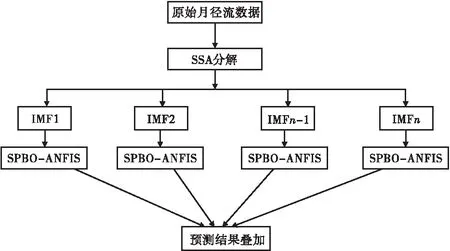
图1 月径流时间序列预测流程

步骤二利用训练样本均方误差构建目标函数：

(10)

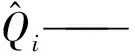
步骤三初始化SPBO算法学生规模N，最大迭代次数Tmax和算法终止条件。

步骤四初评估班级每个学生的初始成绩，根据初始成绩将学生分为4类：最优学生、好学生、普通学生和尝试随机提高学生。找到并保存当前最优学生，并令当前迭代次数t=1。

步骤五判断学生所属类型：利用式(4)更新最优学生成绩；利用式(5)更新好学生成绩；利用(6)更新普通学生成绩；利用式(7)更新尝试随机提高学生成绩。

步骤六评估班级每个学生的当前成绩，找到并保存当前最优学生。

步骤七令t=t+1。判断终止条件，输出全局最优学生，算法结束；否则返回步骤五。

步骤八输出最优学生，即ANFIS最佳条件参数和结论参数。

步骤九将最优ANFIS最佳条件参数和结论参数代入SPBO-ANFIS模型对各子序列分量进行预测，将各分量预测结果加和重构后即为月径流最终预测结果。

步骤十采用平均绝对百分比误差(MAPE)、平均绝对误差(MAE)、纳什系数(NSE)、合格率(PR)对模型有效性进行评估，见式(11)。

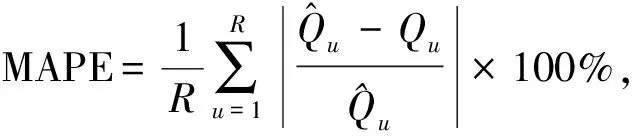
(11)

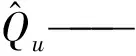
2 实例应用

2.1 数据来源

云南省某水文站控制径流面积203 km2，属国家基本站，观测项目有水位、流量、降雨。本文研究数据来源于该站1960年1月至2012年12月共636个实测月径流时间序列。从图2可以看出，该站月径流时间序列表现出强烈的非线性、非平稳性和多层次性特征。

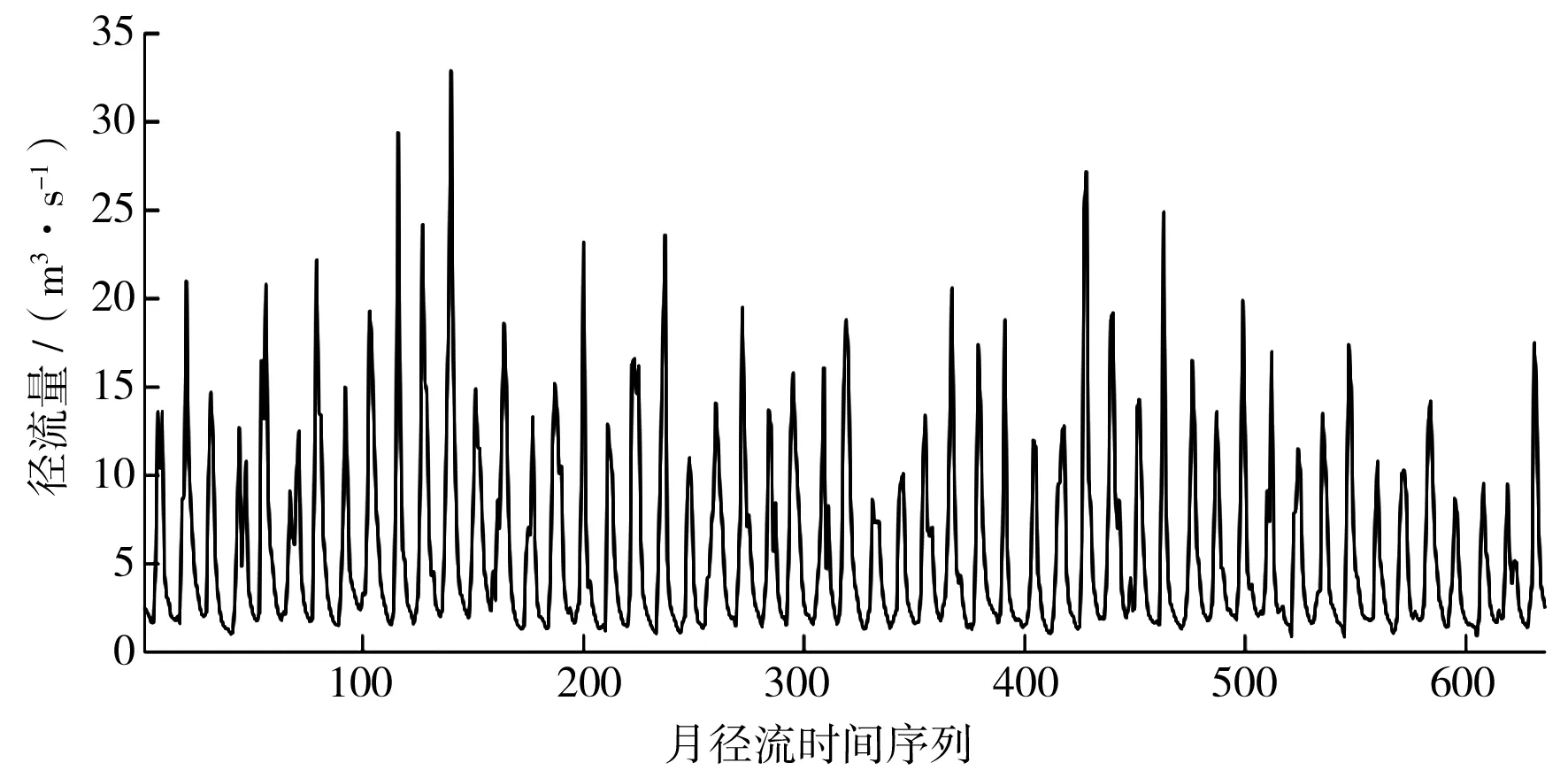
图2 某水文站1960年1月至2012年12月径流变化曲线

2.2 月径流时间序列数据多尺度分解

2.2.1SSA分解

SSA是一种处理非线性时间序列数据的常用方法。研究表明，SSA分解确定子序列数量至关重要，若子序列数量过少，则不足以将原始序列中蕴含的不同成分提取出来；若子序列数量过多，则增加了模型复杂程度和建模工作量[19]。本文通过傅里叶变换(Fourier Transform，FT)方法，并结合月径流显著的年周特性，设置SSA窗口长度L=12，依据SSA原理对实例月径流时间序列数据进行多尺度分解，即将原月径流时间序列分解为12个更具规律的子序列IMF，利用SPBO-ANFIS模型分别对12个IMF进行预测，将预测结果叠加即得到最终月径流预测结果。月径流时间序列SSA分解结果见图3。

a)IMF1

b)IMF2

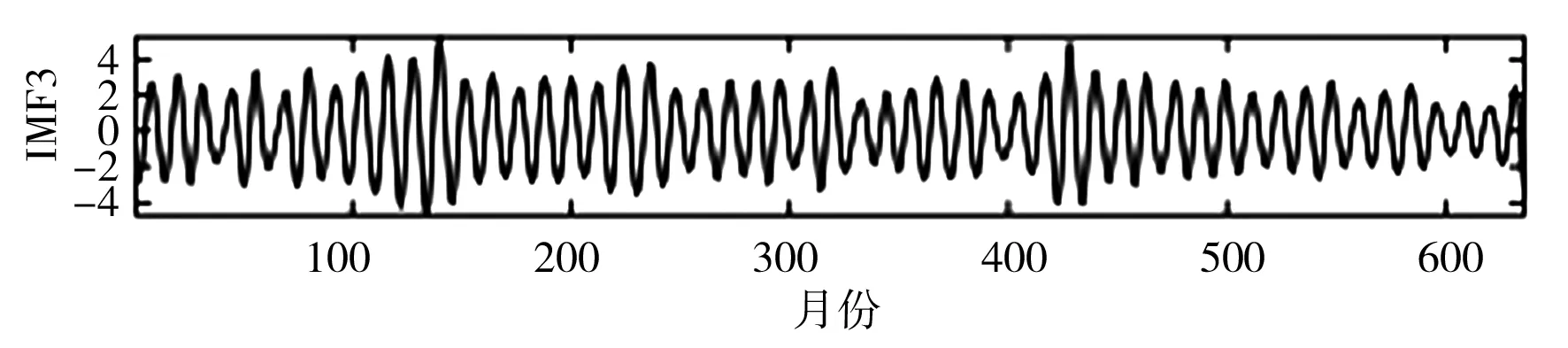
c)IMF3

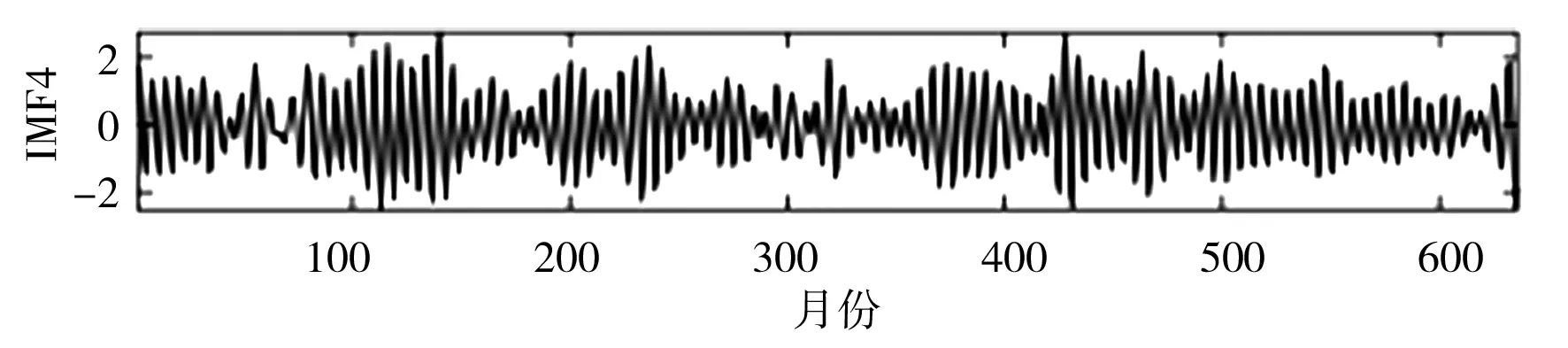
d)IMF4

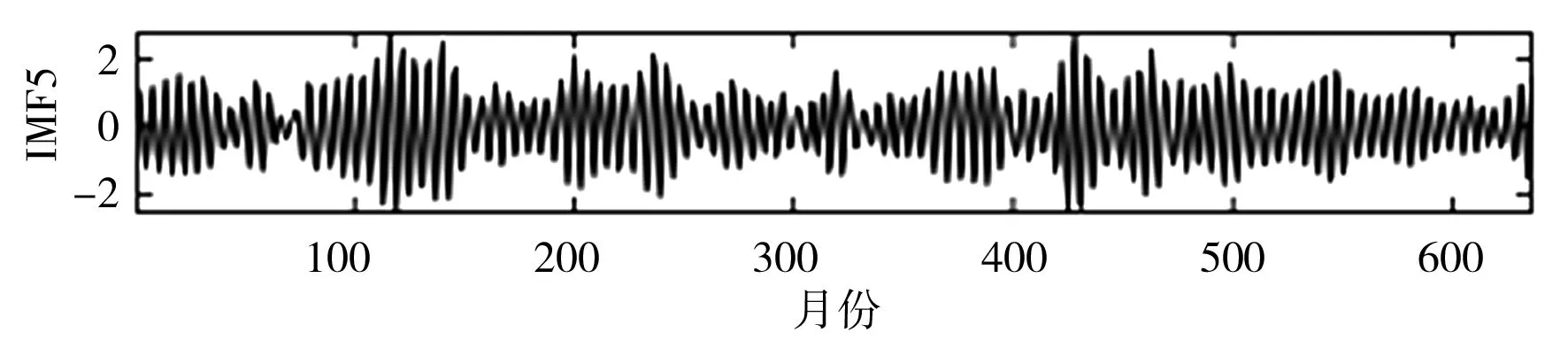
e)IMF5

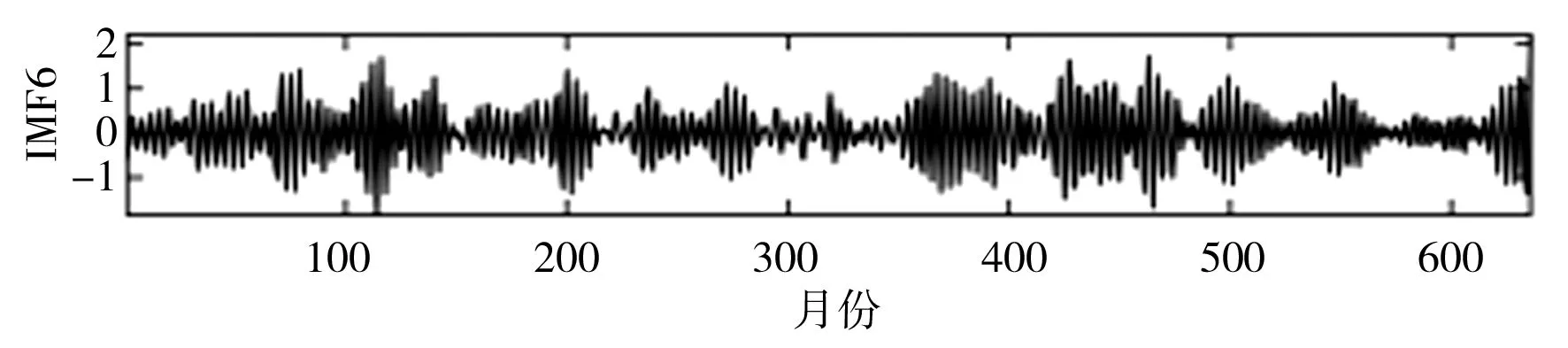
f)IMF6

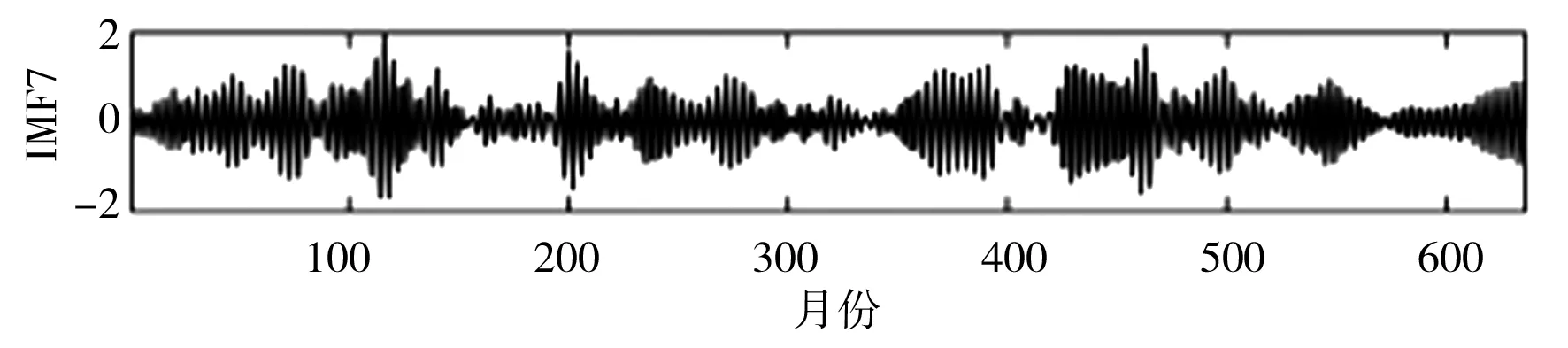
g)IMF7

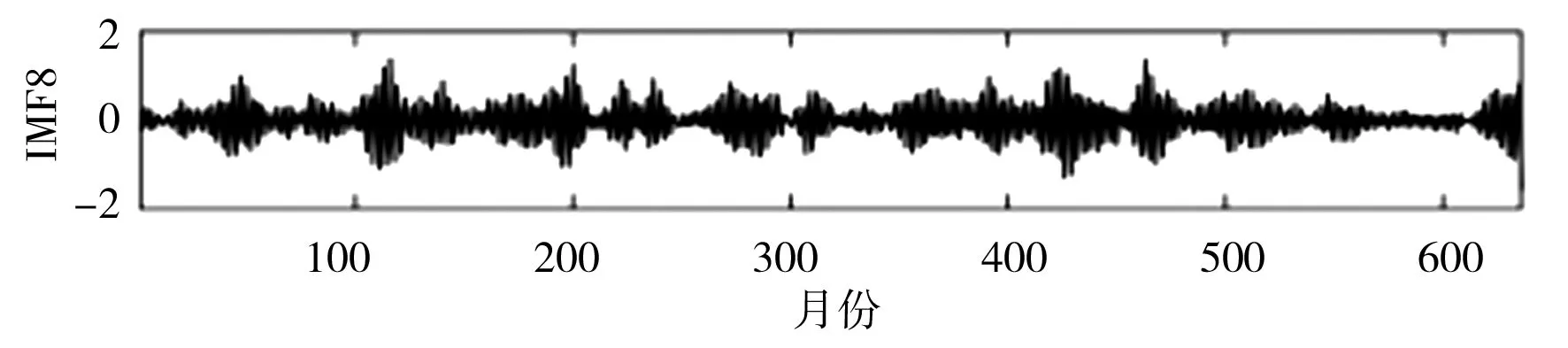
h)IMF8

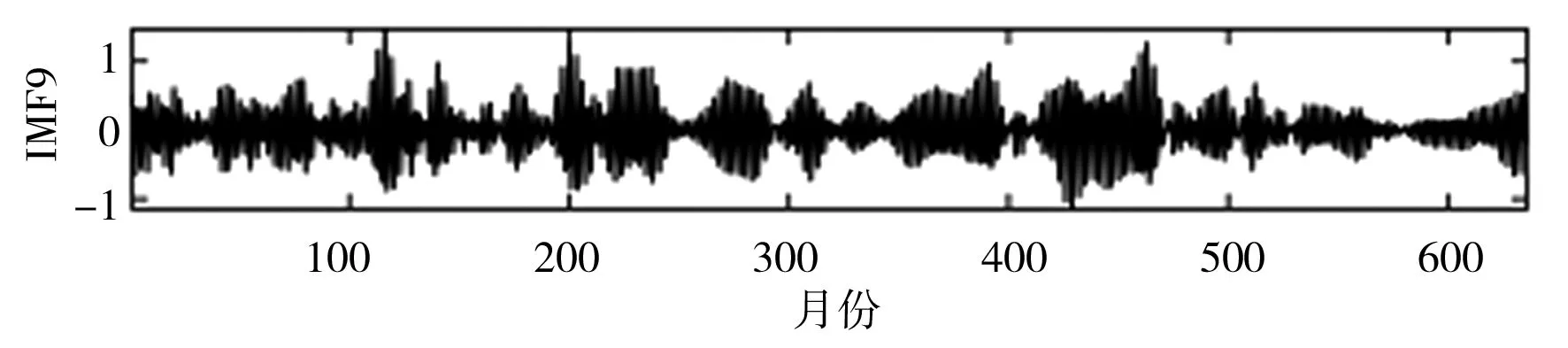
i)IMF9

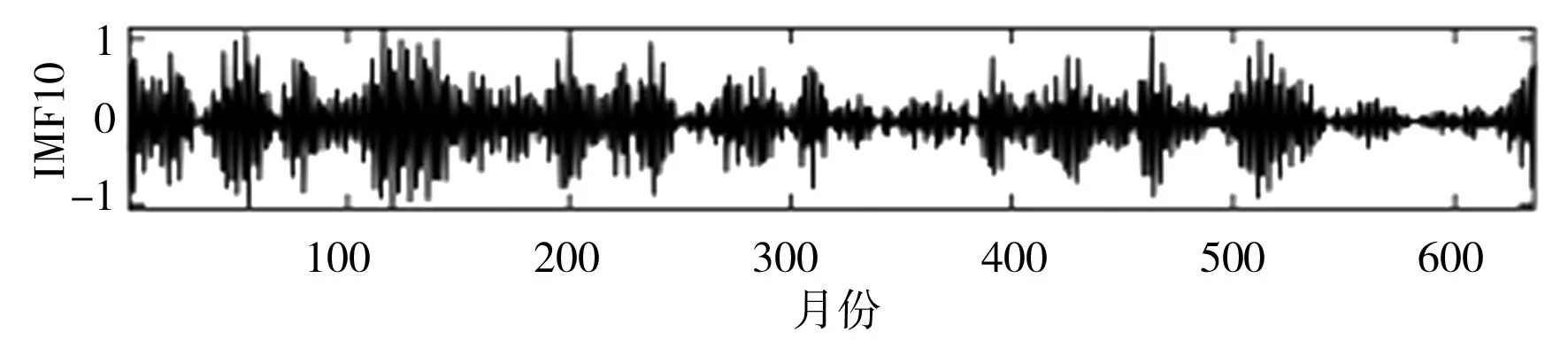
j)IMF10

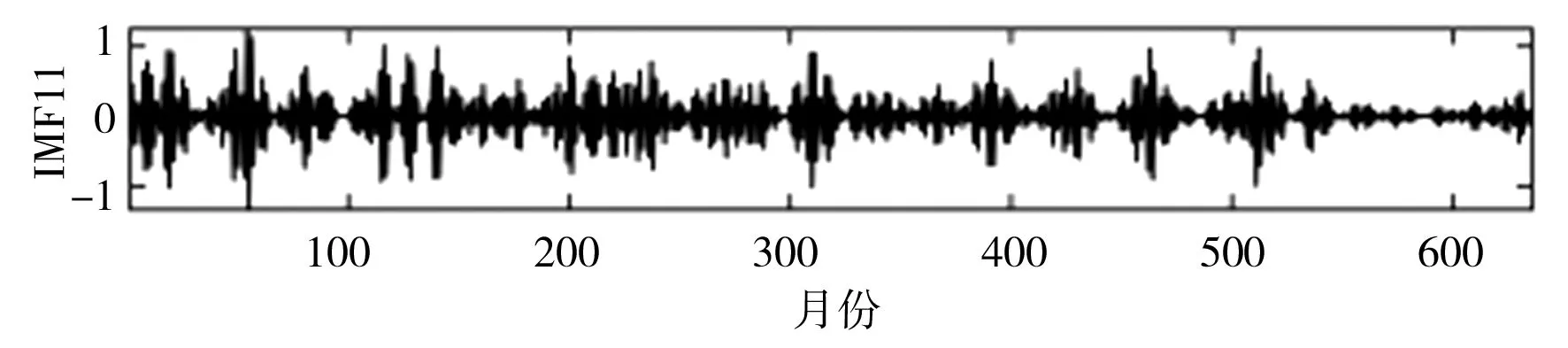
k)IMF11

l)IMF12

2.2.2EEMD分解

利用EEMD方法对实例636个连续月径流数据进行分解。经分解，原始月径流数据分解为9个IMF分量和一个趋势项rse。趋势项rse大致反映原月径流时间序列的变化趋势；IMF1—IMF9反映了原径流时间序列的波动情况。

2.3 确定输入向量

合理确定各IMF输入、输出向量是决定月径流时间序列预测精度高低的关键。目前普遍采用相空间重构的方法确定时间序列输入、输出向量。相空间重构目的是确定延迟时间和嵌入维数，目前延迟时间的确定方法有自相关函数法(AFM)等，嵌入维数确定方法有G-P法、C-C法等。研究表明，对于同一水文时间序列，不同方法确定的延迟时间和嵌入维数可能不同，甚至出差较大，这给确定时间序列输入、输出向量带来困难。

经过反复调试，采用偏自相关函数法(PAFM)或自相关函数法(AFM)综合确定各IMF输入向量，即将各IMF分量自相关系数或偏自相关系数最大时所对应的滞后数H视为最优嵌入维数，即将预测月前H个径流数据作为输入向量，预测月作为输出向量。各IMF输入、输出向量确定结果见表2。本文将实例后120个月作为预测样本。

EEMD分解得到的9个IMF分量和1个趋势项rse的输入、输出向量采用同样的方法确定，限于篇幅从略。

2.4 参数设置及预测分析

2.4.1参数设置

SSA-SPBO-ANFIS、EEMD-SPBO-ANFIS、SPBO-ANFIS模型：SPBO算法学生规模N=50，最大迭代次数T=100；ANFIS模型条件参数和结论参数搜索范围为[-25,25]，初始聚类数目5，分类矩阵指数5，最大迭代次数100，目标误差0.001。

2.4.2预测分析

利用SSA-SPBO-ANFIS、EEMD-SPBO-ANFIS模型对实例各子序列进行预测，将预测结果加和重构后得到实例最终月径流预测结果；并利用SPBO-ANFIS模型对未经分解的原月径流时间序列进行训练及预测。同时，采用平均绝对百分比误差MAPE(%)、平均绝对误差MAE(m3/s)、纳什系数NSE和合格率PR(%)对各模型性能进行评估，结果见表3，预测效果见图4。

表2 各IMF相关系数、嵌入维数及序列长度

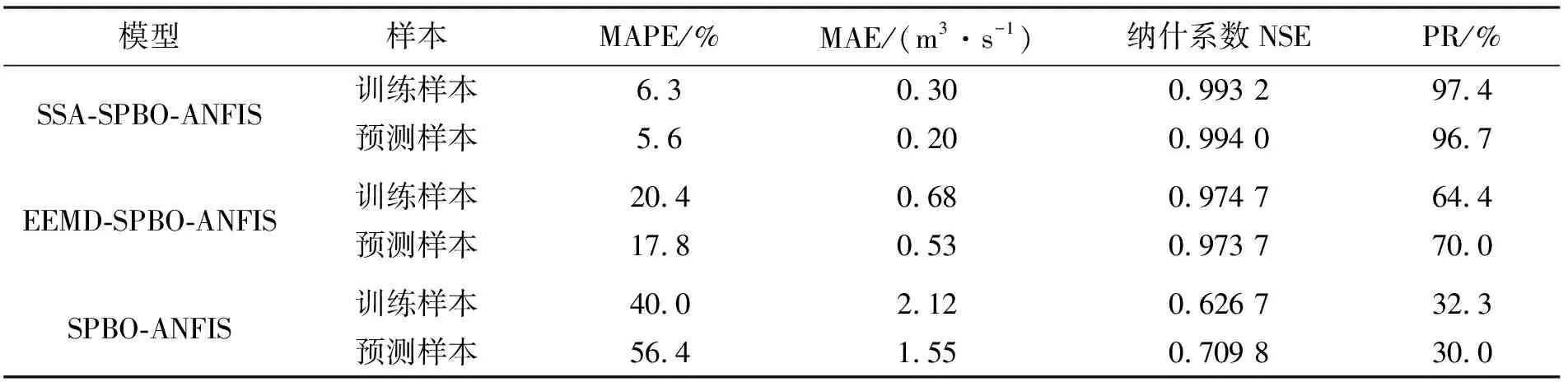
表3 实例月径流时间序列预测结果对比

a)径流量

b)相对误差

c)绝对误差

从表3、图4可以得出以下结论。

a)SSA-SPBO-ANFIS模型对实例月径流时间序列预测的MAPE、MAE、NSE和PR分别为5.57%、0.20 m3/s、0.994 0、96.7%，MAPE分别较EEMD-SPBO-ANFIS、SPBO-ANFIS模型降低68.7%和90.1%，MAE分别降低62.3%和87.1%，NSE分别提高2.1%和40.0%，PR分别提高38.1%和223.3%，拟合、预测效果优于EEMD-SPBO-ANFIS、SPBO-ANFIS模型，具有更小的预测误差和更高的预测精度；SSA能科学将原径流时间序列数据分解成多个更具规律的子序列，显著提高水文时间序列月径流的预测精度。

b)从表3来看，在长达120个月的月径流预测中，SSA-SPBO-ANFIS、EEMD-SPBO-ANFIS模型预测的纳什系数NSE分别为0.994 0和0.973 7，高于SPBO-ANFIS模型预测的纳什系数0.709 8，表明SSA-SPBO-ANFIS、EEMD-SPBO-ANFIS模型预测结果可靠。其中，尤以SSA-SPBO-ANFIS模型的预测效果最好，预测可信度最高。

c)从图4来看，SSA-SPBO-ANFIS模型的预测效果最好，EEMD-SPBO-ANFIS模型次之，SPBO-ANFIS模型最差。SSA-SPBO-ANFIS模型预测结果能够很好地逼近实测径流，对峰值捕捉效果好，具有较小的预测误差和较好的预测效果，将其用于月径流时间序列预测是可行的。

3 结论

基于奇异谱分解(SSA)、学生心理学优化(SPBO)算法和自适应神经模糊推理系统(ANFIS)构建水文时间序列月径流组合预测模型，利用云南省某水文站月径流时间序列预测实例对SSA-SPBO-ANFIS、EEMD-SPBO-ANFIS、SPBO-ANFIS模型进行检验；并通过对SPBO算法仿真测试和比较MAPE、MAE、NSE、PR 4个指标，可以得出以下结论。

a)介绍了学生心理学优化(SPBO)算法。通过8个单峰、多峰测试函数在不同维度条件下对SPBO算法进行仿真验证。结果显示SPBO算法寻优性能优于TLBO算法，将SPBO算法用于ANFIS条件参数和结论参数寻优具有可靠性。

b)SSA-SPBO-ANFIS模型对实例月径流时间序列拟合、预测效果优于EEMD-SPBO-ANFIS模型，远优于SPBO-ANFIS模型。模型有效地提高了月径流时间序列的预测精度，且具有较好的通用性与稳定性，为月径流预测提供了一种新方法。

c)实例验证表明，SSA能有效将复杂非线性和非平稳性的月径流时序数据分解为若干更具规律的子序列，抽取出月径流时间序列的整体趋势和不同周期上的波动情况，同时挖掘月径流时序数据的物理特征和结构信息，提高了模型的预测精度。

d)利用SPBO算法优化ANFIS条件参数和结论参数，不但克服ANFIS模型随机选取参数的不足，而且有效提高了模型的预测精度和智能化水平，可为ANFIS相关预测研究提供参考。