基于关键链技术的进度管理方法研究

2022-05-27关晓迪王文进魏欢欢朱勇锋

人民珠江 2022年5期

马迪，关晓迪，王文进，魏欢欢,3,朱勇锋

(1.西安交通工程学院土木工程学院，陕西西安 710300;2.西安理工大学土木建筑工程学院，陕西西安 710048;3.杨凌职业技术学院建筑工程学院，陕西咸阳 712100;4.长安大学地质工程与测绘学院，陕西西安 710048)

关键链技术是近几年新提出的进度管理方法，该方法的核心思想主要表现在以下几个方面：①以50%完工保证率下的工期估计作为初始工期估计;②以关键链作为整个项目的约束路径，而不是关键路线;③在各链路末端设置缓冲区消除不确定因素的影响;④在项目执行过程中，用监控缓冲区消耗情况的方式对项目整体进行管控。对于关键链技术的研究重点集中在如何科学合理的计算缓冲区的大小，因此缓冲区计算方法成为近年来关键链相关问题研究的热点内容，对于这方面的研究也取得了丰富的成果。

1997年，Goldratt[1]在《关键链》一书中不仅提出了关键链的概念，还提出了一种计算缓冲大小的方法：剪切-粘贴法。1998年，Herroelen等[2]第一次用根方差法来计算缓冲大小，该方法是在剪切-粘贴法的基础上，运用中心极限定理将被切掉时间的根方差作为缓冲大小，即根方差法。2002年，Steyn[3]提出项目总工期服从正态分布，且其均值和方差分别等于关键链上各个工序的均值和方差之和的观点，并且得出在均值上加入缓冲可以提高完工率的结论。2005年，Cohen等[4]将使用能力约束资源的活动的总时间的一半作为能力约束缓冲。2006年，Tukel等[5]提出了资源紧张度求解和网络复杂度求解缓冲区的方法。刘士新等[6]设计了一种考虑工序在资源受限情况下的自由时间的启发式算法，用该方法识别出关键链后，利用根方差法计算缓冲区的大小。2008年，Tenera[7]提出可以采用估计最后一项工序延期的风险来确定项目活动时间，该方法被称为SMC法。褚春超[8]提出了1种考虑资源紧张度、网络复杂度、管理者风险偏好水平的计算缓冲的新方法。Long等[9]引入梯形模糊数来估计项目的不确定性，运用90%完工概率下的时间估计与期望工期的差值作为工序的安全时间。马力等[10]在自由时差方法的基础上考虑到项目中不同活动的资源利用程度不同，设计了1种设定缓冲大小的新方法;Liu等[11]提出了多资源受限问题的启发式算法，在现有启发式算法的基础上作了优化。2009年，杨立熙等[12]提出了开工柔韧性的概念，他认为开工柔韧性小的工序消除级联效应的能力较弱，因此可以在其上适当增加缓冲。2010年，Zhao等[13]运用遗传算法识别关键链，然后用编程方法计算缓冲。2012年，施骞等[14]引入模糊方法度量项目的资源紧张程度，将其与网络复杂度、风险偏好系数相结合来计算缓冲。2013年，张延禄等[15]根据项目复杂性的界定问题，归纳总结出复杂性的基本类型。李俊亭等[16]提出优化关键链多项目进度计划的数学模型和启发式算法的调度模型，采用逆向拓扑排序方式进行调度。2014年，Zhang等[17]提出了基于属性优化的缓冲计算方法。Leach[18]提出了可以参考排队论来设置能力约束缓冲。高亮等[19]尝试将帕累托法则应用于缓冲估计，从缓冲公式设置的层面对已有缓冲估计方法进行修正。2017年，张俊光等[20]提出了基于熵权法的项目缓冲计算模型。2019年，叶宇鸿[21]通过引入Z-number模糊数，运用高延期风险性活动的不确定性对缓冲区计算方法进行了改进。2020年，陈诚[22]综合考虑活动相关性、资源紧张度、网络密度和风险偏好因素，提出了一种新的缓冲计算方法。夏斌[23]对根方差法中缓冲区计算进行了改进，将安全时间的方差、位置权数和风险系数用于根方差法的计算。上述研究成果均有益地推进了缓冲区设置方法的相关研究。

值得注意的是，上述关于缓冲区计算方法的研究主要集中在剪切-粘贴法和根方差法以及对该两种方法的改进上。剪切-粘贴法的优点是易于计算，简洁明了。缺点是缓冲区的大小根据工序数目和工序持续时间的增加而增大，符合线性增长规律。这导致工序足够少时，所估计的缓冲区过小;而工序数量增多时，其估计的缓冲区又过大。而根方差法的优点是符合中心极限定理，在一些工序较多的项目中确定缓冲区的大小相比于剪切-粘贴法更加合理，且符合非确定执行时间累加的统计规律，因此可以尽可能避免缓冲区的尺寸过大或过小。缺点是根方差法使用的前提条件是各工序持续时间相互独立，这在实际工程中很难实现，因此得出的结果会存在一定的误差。本文基于上述研究，引入了信息熵理论，用信息熵来衡量影响缓冲大小的因素，建立了可以综合考虑整体复杂熵、单一复杂熵、施工难度熵、资源约束熵、决策者偏好因素的缓冲区设置模型，并结合根方差法对缓冲区计算公式进行改进，使缓冲区的计算更加科学合理。

1 基于信息熵的缓冲区影响因素度量方法

1.1 信息熵的引入

熵(Entropy)[24]是人们定义的一个热力学参数，作为体系混乱度的量度。本文用信息熵来度量工期压缩后产生的诸多不确定性因素，并在此基础上与根方差法有效结合设置缓冲区，实现进度优化管理。

1.2 缓冲区影响因素的度量

在实际工程中，影响工序工期的因素有很多，本文主要考虑了4种最具代表性的因素：网络复杂度、施工难度、资源约束情况和决策者偏好因素。

a)网络复杂度分为整体复杂度(C)[25]和各工序单一复杂度(ci)，整体复杂度反映的是各网络计划活动之间的紧前与紧后约束关系的复杂程度。各工序单一复杂度ci为网络计划中工序i的复杂程度[23]。由于系统的复杂性、规模与熵值成正比，因此，C和ci可分别用整体复杂熵(Hf)和单一复杂熵(Hfi)来度量，整体复杂熵和单一复杂熵越大，表明工程项目和工序受不确定因素的影响越大，工程延期的可能性越大。整体复杂度C和各工序单一复杂度ci的公式为：

(1)

(2)

式中Kj——节点j的紧前工序数;Sj——节点j的紧后工序数;N——项目网络计划中的节点数;A——与其对应的工序数;Li——工序i的紧前工序数;Lt——工序i所在链路的工序总数。

将C和ci代入信息熵公式，得到整体复杂熵Hf和单一复杂熵Hfi的表达式为：

Hf=-ClnC

(3)

Hfi=-cilnci

(4)

b)施工难度。在项目施工的过程中，工序难度越大，其不确定程度就会越高，完工概率就会越低。由于系统施工难度可用信息熵度量，施工难度越大，熵值越大，因此，施工难度可用施工难度熵Hai来表示，本文通过专家评估的方式可以得出表1中各个工序的施工难度系数ε值，其中施工难度熵的计算公式为：

Hai=-εilnεi

(5)

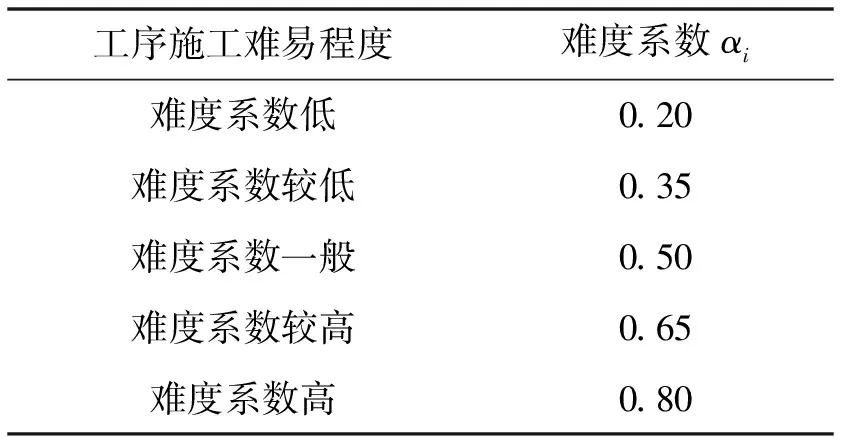
表1 施工难度系数

c)资源约束情况可以通过资源紧张度来度量，资源紧张度可以侧面反映项目的混乱程度，因此，资源紧张度αi可用资源约束熵Hbi度量，资源约束熵越大，工序受资源约束的影响就越大，项目延期的风险相应越大。资源紧张度与资源约束熵的计算公式为：

(6)

Hbi=-αilnαi

(7)

式中Rt——项目在t时段资源供应限量;rkt——t时段执行工序k所需的资源量;m——t时段执行的工序总数;STi——工序i的开始时间;Di——工序i的工期;αi——工序i的资源紧张程度。

d)由于人的行为心理学因素(学生综合症、帕金森定律等)的存在，决策者偏好因素对项目进度的影响很大，主要表现为拖延至最后一刻再完工、估计工序工期时预留大量的冗余时间、工作提前完工不汇报等。

本文用决策者偏好指数λi对决策者偏好因素进行度量，为了更好地度量决策者偏好指数，笔者总结概括了6种最具代表性的影响因素(施工难度、工序相对位置、不确定系数、风险水平、工序复杂度、工序持续时间比例)，并给出了具体的计算方法。

a)施工难度。在工程施工过程中，其施工难度越大，相应所需工期越长，完工概率越低。通过专家评估的方式可以得出各个工序的施工难度系数，施工难度系数见表1。

b)工序相对位置。在工程施工过程中，工序的相对位置会对工序工期造成影响。对于任一工序i，工序位置可以用工序i时间中点距离开始节点的最长距离Li和工序i所在链路总工期最大值Ti的比值来表示，由于工序距离开始节点越近或离终止节点越远时，对工序工期的影响越大，因此工序相对位置ωi的计算公式为：

(8)

c)不确定系数。计划评审技术中的三时估计值是专家和技术人员通过以往经验对工序工期乐观、悲观、最可能时间的相应把控，可以用来表示工序的不确定性。因此，工序的不确定系数K可用最可能时间m与乐观时间a的差和悲观时间b与乐观时间a的差的比值来表示，见式(9)：

(9)

d)风险水平。实际工程中，项目管理者可能根据各种外在条件的不同采取不同的风险水平进行管理。若选取风险偏好水平为ρ，则保证率为1-ρ时所对应的标准差倍数fg，可得该风险水平下工序工期的调整系数ψi表达式为：

(10)

e)各工序单一复杂度。Oya等[26]提出了链路复杂度的思想，即各工序的复杂度可以用其所在链路的复杂度来表示。因此，本文主要应用各工序单一复杂度ci来衡量其对工期的影响，见式(2)。

f)工序持续时间比例。在实际工程中，各工序持续时间越长，其面临风险的可能性越大。因此本文采用工序工期ti与所在链路总工期最大值Ti的比值来表示该工序持续时间对总工期可能造成的影响。则工序持续时间比例计算公式为：

(11)

因此，计算决策者偏好指数λi分为以下3个步骤：首先利用层次分析法计算各因素的权重向量wi，然后逐一计算工序工期的6个影响因素指标值，最后运用式(13)逐个计算决策者偏好指数：

λi=w1·εi+w2·ωi+w3·ki+w4·ψi+

w5·ci+w6·χi

(12)

2 缓冲区设置的熵模型

2.1 基于模糊理论的安全时间估算

Kaufman等[27]提出了一致性指数(AI)的概念，它是衡量两个模糊事件一致性的指标。对于模糊事件A、B，其一致性为模糊事件A相对于模糊事件B的一致程度，一致性指数AI(A,B)可以用A、B的面积来表示，其计算公式为：

(13)

在此基础上，可以转化为基于三角模糊数的一致性表达式[28]：

(14)

(15)

式中h——工序工期的一致性真度。

在传统缓冲区设置方法中，剪切-粘贴法与根方差法中采用工序持续时间的一半作为安全时间，这显然不符合工程实际。本文将安全时间进行改进，采用真度为90%的项目工期与新定义的模糊工期的差值作为工序的安全时间，见式(16)：

(16)

工序i的模糊工期计算公式为：

(17)

2.2 缓冲区模型的建立

通过对缓冲区影响因素的度量，可以得出整体复杂熵Hf、单一复杂熵Hfi、施工难度熵Hai、资源约束熵Hbi和决策者偏好因素λi的计算方法。基于此，运用根方差法可以构建出新的缓冲区设置模型，新的项目缓冲计算方法为：

(18)

式中 PB——初始项目缓冲；n——关键链上的工序数。

同理，汇入缓冲计算方法为：

(19)

式中 FBn——第n条非关键链的汇入缓冲；Hfj——第n条非关键链上工序j的单一复杂熵；Haj——施工难度熵；Hbj——资源约束熵；λj——决策者偏好因素；σj——工序j的安全时间。

2.3 缓冲区的修正

新构建的项目缓冲和汇入缓冲设置模型较原始根方差法所得模型有了很大的改进，但是仍可能存在以下情况：非关键链加入汇入缓冲后大于关键链，导致关键链发生改变;关键链上活动不能连续执行等。为了保证关键链不会发生转变且关键链上的工序可以正常进行，可以通过比较各条非关键链所设置的汇入缓冲与该非关键链上最后一个工序的自由时差的大小，取较小者作为最终设置的汇入缓冲的大小。

首先用Fh表示第n条非关键链上最后一项工序h的自由时差。

(20)

式中Bj——第n条非关键链上最后一项工序h的所有紧后工序的集合;ESj——工序j的最早开始时间;EFh——工序h的最早完成时间。

取汇入缓冲和该非关键链上最后一个工序的自由时差的最小值作为最终汇入缓冲，见式(21)[29]：

(21)

然后计算第n条非关键链的冗余缓冲：

(22)

若自由时差小于汇入缓冲，则汇入缓冲与自由时差之差将不被计入最终的汇入缓冲，修正后的汇入缓冲较本该设置的汇入缓冲偏小，可能出现总工期延误的情况。因此将冗余缓冲Δtn整合到项目缓冲之中，吸收可能出现的风险(图1)。

图1 修正后项目缓冲示意

修正后的项目缓冲PB′为：

(23)

3 算例分析

选取江西省某一高层商业建筑的工程实例，本商业建筑地下1层，地上32层，裙房2层。其计划开工时间为2018年7月1日，计划完成时间为2019年12月18日，总施工日历天数为536 d。因其处于较繁华地段，且地下结构复杂，工程施工跨越冬季施工阶段，最终该项目于2019年12月30日竣工，工期延后12 d。其中项目的进度计划双代号网络见图2，通过与新定义的模糊工期相结合，可得到该工程的关键路线P1-P2-P6-P7-P8-P9-P11-P13-P20-P21-P22-P23-P24，见图3。在关键路线的基础上消除资源约束，就可以得到关键链P1-P3-P5-P8-P9-P11-P13-P20-P21-P22-P23-P24，相应的关键链网络见图4。

图2 初始项目进度计划双代号网络

图3 与模糊工期相结合的双代号网络

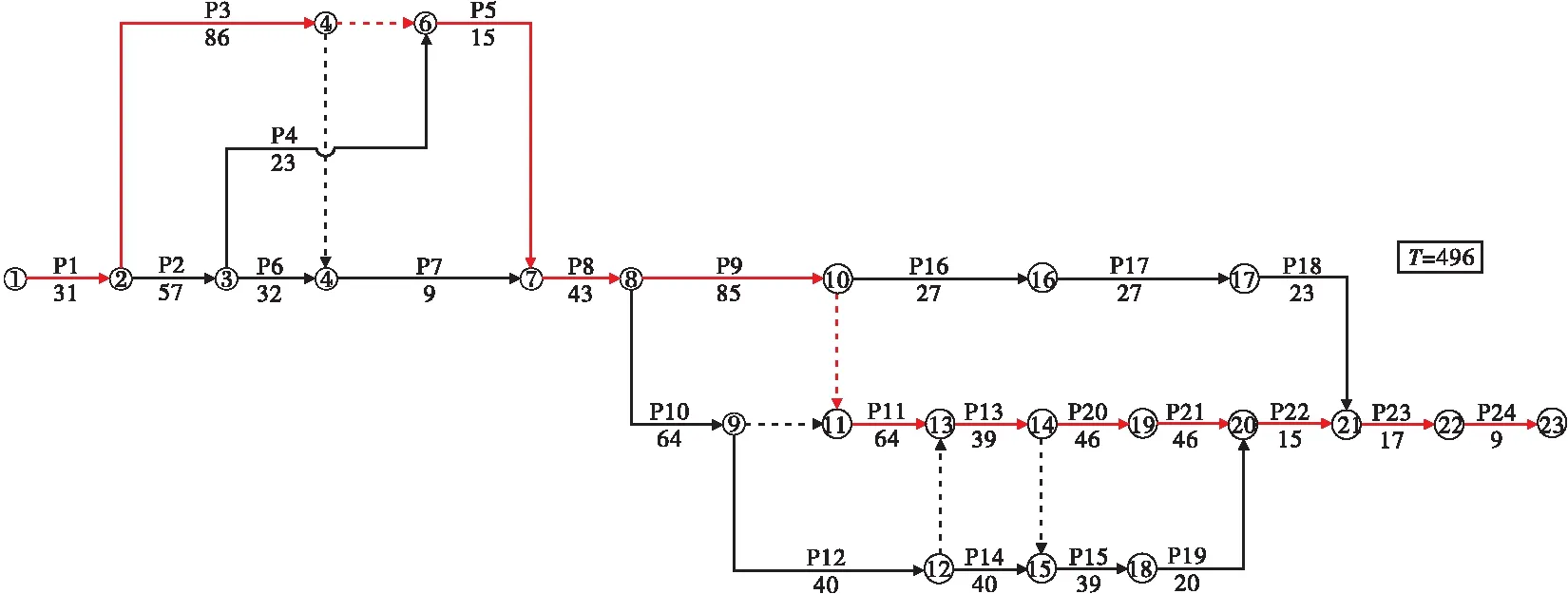
图4 基于模糊工期的关键链

a)基于信息熵的各缓冲区影响因素度量结果分别如下。

整体复杂熵(Hf)：N=23，A=24，C=0.020 9，Hf=0.080 8。

单一复杂熵(Hfi)：由图4可知，共有6条非关键链，分别为：P2-P4，P2-P6-P7，P10，P10-P12，P16-P17-P18，P10-P12-P14-P15-P19。对于每一条非关键链上的工序，其单一复杂熵计算结果分别为：非关键链P2-P4中Hf2=0，Hf4=0.346 6;非关键链P2-P6-P7中Hf2=0，Hf6=0.366 2，Hf7=0.270 3;非关键链P10中Hf10=0;非关键链P10-P12中Hf10=0，Hf12=0.346 6;非关键链P16-P17-P18中Hf16=0，Hf17=0.306 5，Hf18=0.178 5;非关键链P10-P12-P14-P15-P19中Hf10=0，Hf12=0.321 9，Hf14=0.366 5，Hf15=0.306 5，Hf19=0.178 5。

经计算，得到施工难度熵Hai、资源约束熵Hbi、决策者偏好指数λi和安全时间σi见表2。

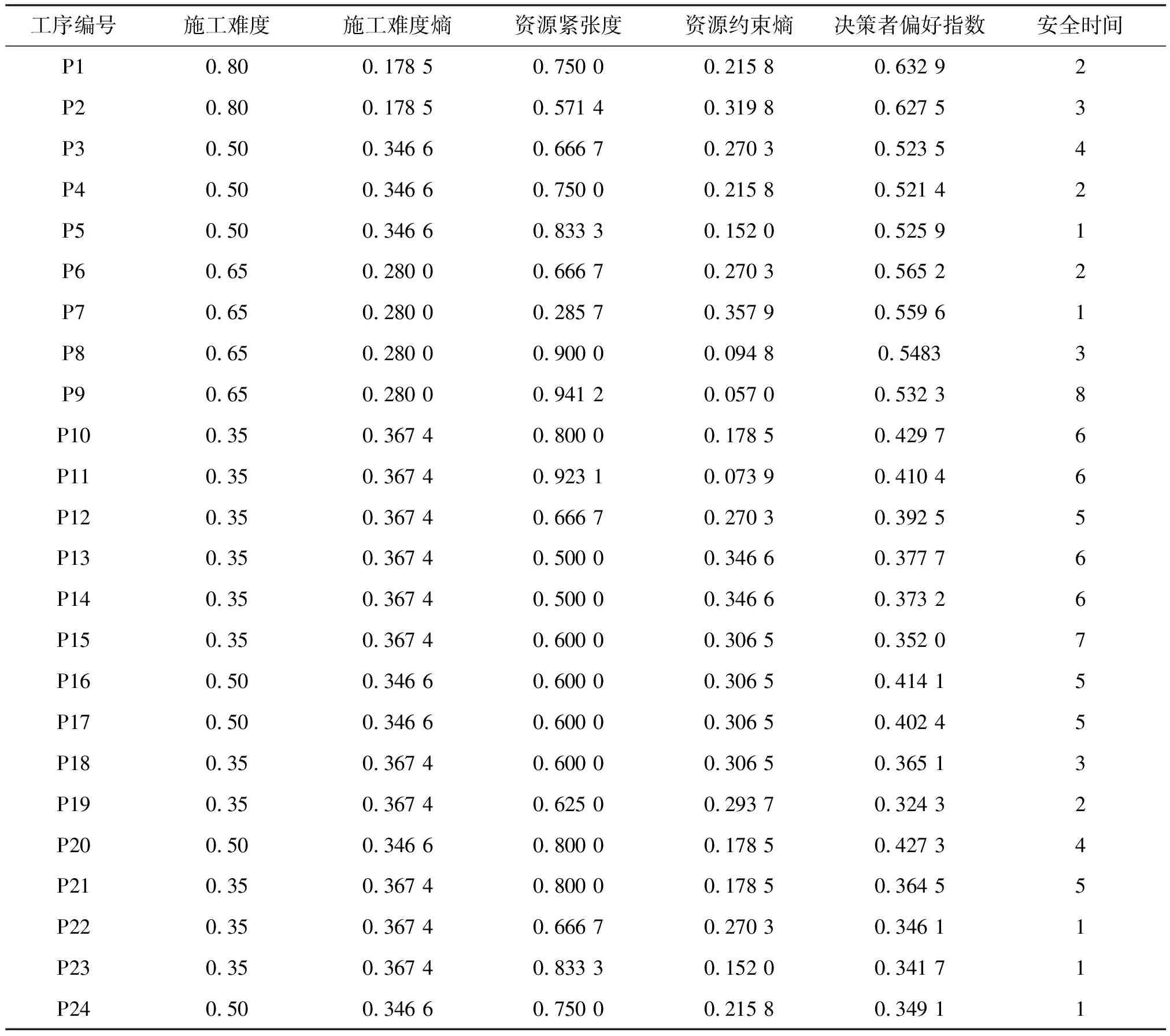
表2 施工难度熵、资源约束熵、决策者偏好指数和安全时间

b)缓冲区的计算。将项目缓冲PB设置在关键链上最后一个工序P24的后边，项目缓冲PB的计算结果如下：

=12 d

(24)

汇入缓冲需要设置在非关键链汇入关键链处。工程共有6个非关键链，因此需要设置6个汇入缓冲。根据分析需分别设置在工序P4、P7、P10、P12、P18、P19的后边。

对于非关键链P2-P4，在P4后边设置汇入缓冲FB4：

(25)

对于非关键链P2-P6-P7，在P7后边设置汇入缓冲FB7：

(26)

对于非关键链P10，在P10后边设置汇入缓冲FB10：

(27)

对于非关键链P10-P12，在P12后边设置汇入缓冲FB12：

(28)

对于非关键链P16-P17-P18，在P18后边设置汇入缓冲FB18：

(29)

对于非关键链P10-P12-P14-P15-P19，在P19后边设置汇入缓冲FB19：

FB19=

(30)

由于汇入缓冲均小于各非关键链上最后一项工序的自由时差，因此项目缓冲保持不变。该工程的关键链长度为496 d，项目缓冲为12 d，则总工期为508 d。原计划总工期为536 d，且实际施工后工期延误12 d，因此使用传统方法的总工期为548 d，本文方法较传统方法提前了40 d，并且在传统方法的基础上消除了资源约束问题，更加科学合理。