非理想声学黑洞薄板的阻尼减振研究

田 晓， 刘灿昌*， 胡红中， 汪 灿， 曹帅康

(1.山东理工大学 交通与车辆工程学院， 山东 淄博 255049； 2.延边大学 工学院， 吉林 延边 133002)

0 引言

薄板结构广泛应用于当今工业生产中，具有结构简单、质量轻便等特点，可用于航空航天、汽车、建筑和航海等领域[1-3]，其减振降噪性能成为研究的热点之一.

薄板中嵌入满足幂律变化的声学黑洞(Acoustic Black Hole，简称ABH)结构[4]，在理想情况下，沿薄板厚度变小方向传递的弯曲波能量在末端位置能被吸收从而达到减振降噪的目的.然而受到现实加工技术的限制，理想的声学黑洞结构很难制造，薄板厚度始终无法接近于零，这就使得它存在一定厚度的截断[5,6]，会增加其反射量，从而影响声学黑洞的减振降噪性能.为了弥补这一缺陷，可在声学黑洞区域敷设阻尼层材料，使其振动能量转移到阻尼层上进行耗散[7-13].Ouisse M等[14]通过改变粘贴在声学黑洞区域的阻尼材料的温度来控制其减振性能.Deng J等[15]使用由粘弹性层和约束层构成的被动约束粘弹性层放置于声学黑洞梁末端，与无约束的常规粘弹性处理的梁相比，得出前者可以提高其减振性能.

近年来，研究学者开始关注具有特殊物理性质的人工复合材料[16]，特别是环氧树脂，常作为复合材料制作的基体材料.但实际生产的树脂材料的结构减振性能会受截断的影响，有研究学者[17]为减小这种影响，将声学黑洞的楔形结构在树脂薄板上等距离拉伸，改变声学黑洞结构之间的距离来控制薄板的隔声效果.

本文主要研究单个声学黑洞结构，设计了一种基于环氧树脂材料的非理想声学黑洞薄板，结合其能量聚焦特点，通过仿真和实验对比了不同敷设半径和厚度的阻尼层材料对振动的抑制效果.

1 声学黑洞基本原理及模型

在具有声学黑洞效应的结构中，其边界的理想厚度为零，厚度变化满足幂律关系h(x)=εxm，ε表示一个常数，称为黑洞效应因子.弯曲波在向一维声学黑洞结构边缘位置传播时，任意一点产生的积分波相位φ表示为：

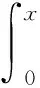
(1)

式(1)中k(x)又可以具体表达为：

(2)

式(2)中：kp表示结构中弯曲波的波数，结合式(1)可得当m≥2，可以看出式(2)的结果是不收敛的，φ也趋向于无穷大.在这种情况下，弯曲波无法到达一维声学黑洞结构边缘处，因而不会产生波的反射[18].弯曲波的能量被聚集在一维声学黑洞结构末端，从而形成"声学黑洞"现象.二维声学黑洞结构是由一维声学黑洞结构以尖端为中心旋转一周所得.当薄板结构的厚度变化满足幂律关系且指数大于等于2就可以满足声学黑洞结构的基本条件，此时弯曲波才有可能到达声学黑洞结构中心从而被吸收.

本文设计了一种非理想声学黑洞薄板，外形尺寸为300 mm×200 mm×5 mm，材料类型为环氧树脂，密度ρ1=1 180 kg/m3，泊松比σ1=0.368，杨氏模量E1=1 Gpa.矩形薄板中心制造半径为ra=40 mm，黑洞区域厚度变化满足h(x)=εxm，其中ε=0.617 3，m=2.这里考虑到实际加工原因，并不能使声学黑洞中心区域的厚度无线接近于零，则考虑截断的厚度h0=0.5 mm，截断的半径为r0=5 mm.

2 有限元模型分析

2.1 能量聚集效应

基于上文表述的模型结构，通过多物理场仿真软件COMSOL Multiphysics建立如图1所示四周固定约束的非理想声学黑洞薄板模型，并建立等条件的均匀矩形薄板(Uniform Plate，简称UTP)模型.两模型分别在0～3 000 Hz进行频率响应分析，并在模型点(-0.11，0.005，0.1)m处施加大小为1 N的简谐激励，然后在点(0.11，0，0.1)m处提取振动速度.

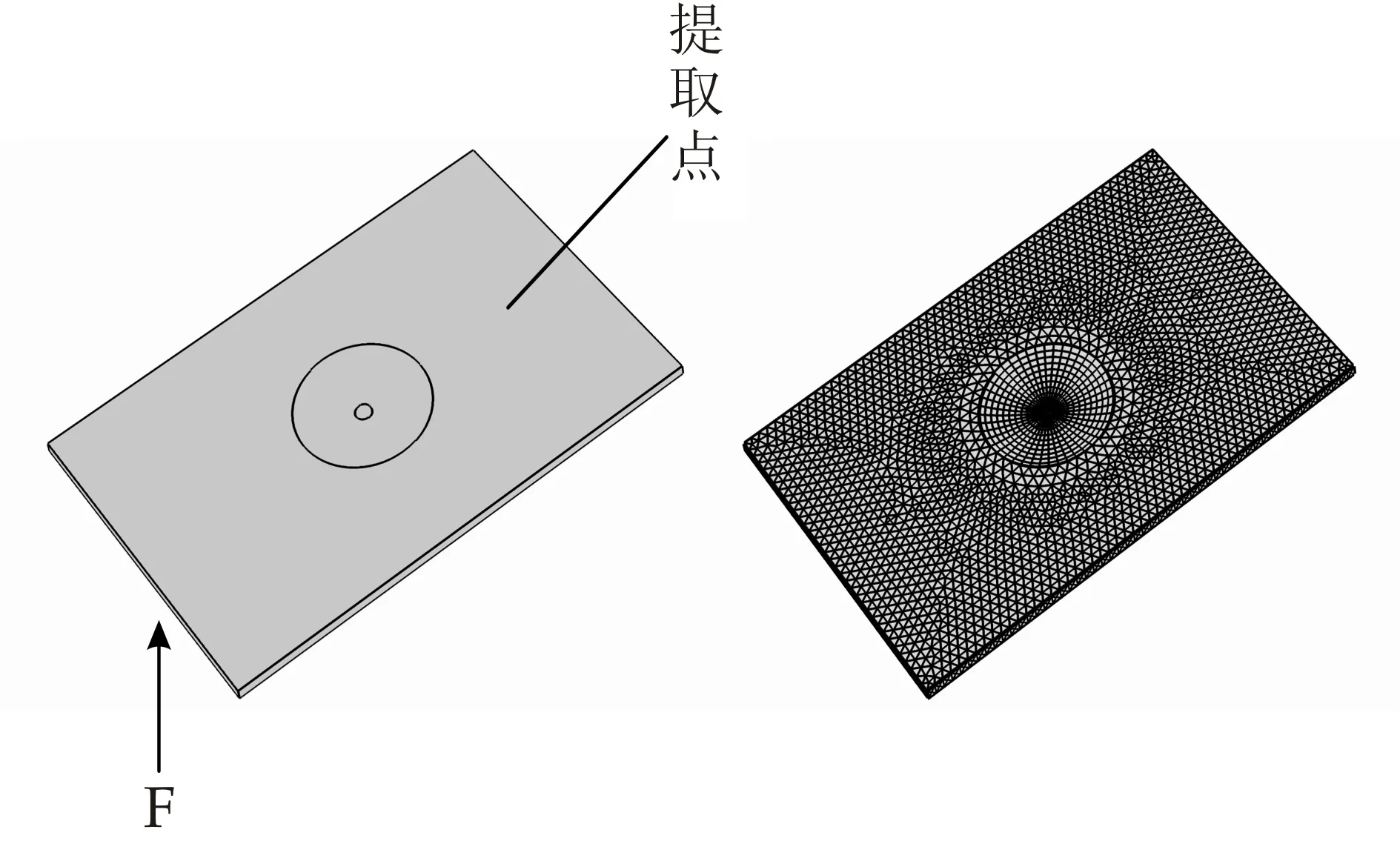
图1 有限元模型与网格划分

图2分析均匀矩形薄板和声学黑洞薄板的振动速度级.能够看出，在0～500 Hz频段内均匀薄板和声学黑洞薄板的共振峰值出现在不同的频率，但两种结构的振动响应曲线峰值的高度却大致相同.在500 Hz以后的频段，声学黑洞薄板的振动峰值有所下降，在个别峰值高于均匀薄板.这表明仅仅嵌入非理想声学黑洞结构并不能对结构起着显著的振动控制效果，这是因为声学黑洞中心最小厚度不是零，即使是很小的截断，也会使其反射系数增加50%～70%[19]，因此能量振动会反射到薄板上的其他区域.

图2 均匀薄板与声学黑洞薄板振动响应对比图

图3得到了在不同频率下均匀薄板和声学黑洞薄板的振动能量云图.能够看出，能在800 Hz频率时，声学黑洞薄板相对于均匀薄板的能量聚集效果不明显，原因是因为在低频段时，弯曲波波长较长，会绕过黑洞区域传递.随着频率的升高，可以明显看出振动能量聚集于黑洞区域.具有截断的声学黑洞结构不能很好的抑制振动控制效果，但依旧可以起着能量聚集作用，这与文献[20]的研究结论一致.可将阻尼层附加在声学黑洞区域，达到集中耗散振动能量的目的.

(a)频率800 Hz(UTP) (d)频率800 Hz(ABH)

2.2 阻尼减振分析

在振动过程中，阻尼是物体由于外界激励或物体本身具有的原因引起的振动幅值下降的特性，通常用其来表示振动能量衰减效率.在力学中，导致物体振动减弱的阻尼因素有很多，主要包括材料的自身阻尼、周围介质对振动的阻尼、连接构件间的摩擦阻尼和热弹性阻尼等.而对于非理想结构构成的振动系统而言，介质阻尼引起的振动能量衰减是系统耗散振动能量的重要机制，因此将对非理想声学黑洞薄板的阻尼减振特性进行研究.图4设计了不同阻尼层敷设半径r结构图.阻尼层材料密度ρ2=920 kg/m3，泊松比σ2=0.49，杨氏模量E2=30 MPa，损耗因子υ=0.9，阻尼层厚度h=0.5 mm.

图4 不同阻尼层半径的声学黑洞薄板

图5分析了不同阻尼层半径的声学黑洞薄板振动速度级.能够看出，阻尼层半径为10 mm和20 mm的ABH薄板共振峰相比未敷设阻尼层的ABH薄板共振峰在2 000 Hz内的中低频段没有明显的振动衰减效果.从2 000 Hz以后，阻尼层半径为10 mm和20 mm的ABH薄板共振峰值开始降低，但在2 500 Hz后的某些频段仍然会高于未敷设阻尼层的ABH薄板.半径为40 mm的ABH薄板在全频段有着明显的共振峰衰减效果，特别是在1 500 Hz以后的频段，相比于未敷设阻尼的ABH薄板峰值平均可降低15 dB以上，且结构振动起伏趋于平缓.

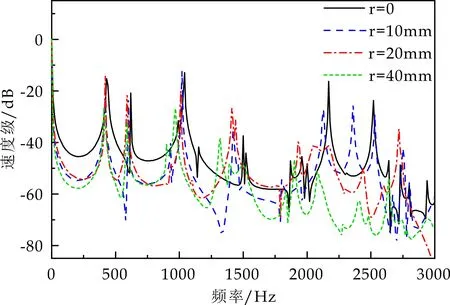
图5 不同阻尼层半径的声学黑洞薄板振动响应

图6设计了不同阻尼层的声学黑洞薄板结构图，基于上文敷设半径为r=40 mm，改变阻尼层厚度h，分析其减振效果.

图6 不同阻尼层厚度的声学黑洞薄板

图7得到了不同阻尼层厚度的声学黑洞薄板振动速度级对比图.能够看出，阻尼层厚度的改变在对ABH薄板的振动控制起到了明显的效果，敷设阻尼厚度为1 mm和1.5 mm的ABH薄板相比敷设阻尼厚度为0.5 mm的ABH薄板共振峰值有所减小，厚度为1 mm时在全频段可平均减振1.2 dB，厚度为1.5 mm时在全频段可平均减振4.1 dB.

3 实验研究

3.1 实验平台搭建与模型验证

为了验证仿真结果的准确性，本文搭建了如图8(a)所示的实验平台.设备通电后，由信号发生器输出信号到功率放大器，经功率放大器放大信号到激振器从而引起实物模型的振动.实验样板用螺栓四周固定，将激振器激振点使用螺栓安装在如图8(b)所示的测试样板下端激励点处，在其上表面另一侧采集点处固定单轴加速度传感器，用石蜡与薄板粘贴在一起，另一端与多通道加速度传感器相连，在输出端用网线接口与计算机相连，用于实验数据的输出.

(a)实验平台 (b)实验样板图8 实验平台与测试样板

实验测试薄板所用材料为环氧树脂，尺寸大小按照上文仿真模型保持不变.通过图8(a)所示的实验装置进行1～3 000 Hz频率响应分析，得到加速度幅值.在图9中，实验设备测量得到的是振动加速度幅值g，经对比中可以发现，ABH薄板实验和仿真大多数响应峰值匹配的相对较好，任何两个峰值之间的最大频率差小于70 Hz.某些频段产生差异的原因可能是固定方式与理论上的约束方式稍有差异以及加工过程中存在的误差，会略微改变振动峰值出现的频率，但它们总体的幅值趋势可以说是一致的，因此可以证明仿真模拟的可行性.

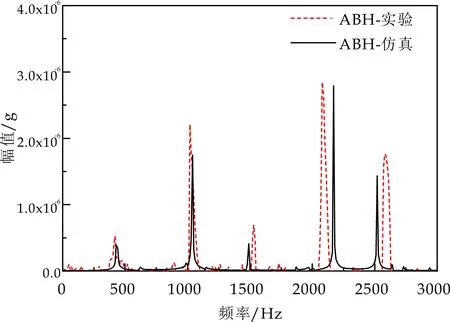
图9 声学黑洞薄板实验与仿真对比图

3.2 阻尼减振实验研究

如图10所示，将材料为丁基橡胶的阻尼层敷设于黑洞区域底部.对实验样板在1～3 000 Hz频率范围内施加幅度为10 Vpp的白噪声点激励.理论分析所用简谐激励，变化较为单一，测量结构其振动速度级便可很好的观察其减振效果，而试验分析所选用的白噪声激励，能够更好的观测全频带的振动响应，且符合应用环境的复杂性.加速度则是反应设备结构内部各种力的综合作用，利用加速度传感器提取其加速度，所得数据更加准确.实验至少测量5次，取其平均值，经计算机处理得到振动加速度传递率.

图10 敷设阻尼层的实验样板

保持阻尼层厚度h为0.5 mm不变，图11分析了敷设不同半径r的阻尼层对ABH薄板的振动控制效果，能够看出敷设三种不同半径阻尼层的ABH薄板相比未敷设阻尼层的ABH薄板呈现较低的响应水平.随着阻尼层半径的增加，阻尼层敷设面积越大的ABH薄板减振效果越明显.随着频率的升高，半径为40 mm的阻尼层减振幅度开始增加，在500 Hz后的中高频段平均减振5.7 dB，在某些频段可以降低振动峰值15 dB以上.

图11 不同阻尼层半径的声学黑洞薄板加速度传递率响应

保持阻尼层半径为40 mm不变，改变阻尼层敷设厚度.在原有0.5 mm厚度的基础上，进行阻尼层加厚.图12分析了两种加厚阻尼层相比原厚度阻尼层的振动抑制效果，能够看出阻尼层的加厚可使结构在全频段振动响应降低，随着频率的升高，振动的幅度逐渐趋于平缓.敷设厚度为1 mm的ABH薄板相比阻尼厚度为0.5 mm的ABH薄板平均减振约1.4 dB，而厚度为1.5 mm时可平均减振4.2 dB.

图12 不同阻尼层厚度的声学黑洞薄板加速度传递率

4 结论

本文建立一种含有声学黑洞结构的环氧树脂矩形薄板模型，采用有限元仿真对比研究了均匀薄板与非理想声学黑洞薄板的能量聚焦效应，并通过仿真和实验研究了非理想声学黑洞区域下方敷设半径和厚度不同的阻尼层对结构振动的抑制效果，得到了以下结论：

(1)含有截断的非理想声学黑洞薄板具有能量聚集效果，中高频段的聚集效果优于低频段，但没有敷设阻尼层的非理想声学黑洞薄板相比于均匀薄板减振效果不明显.

(2)将阻尼层敷设于非理想声学黑洞区域下方能够有效地削减截断处的影响从而衰减振动能量，敷设同一尺寸阻尼层的非理想声学黑洞薄板减振幅度随频率升高而增大.

(3)随着阻尼层敷设半径的增加，阻尼层敷设面积增大，对非理想声学黑洞薄板的结构振动抑制越来越强，原有阻尼层的加厚也能够进一步加强结构的振动衰减幅度.