四边形在生活中的运用

曹渊

华罗庚说过：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，日用之繁，无处不用数学。”这是对数学与生活的精彩描述。数学源于生活，又服务于生活，数学与生活是密不可分的。

例如，要检验一个门框是不是矩形，我们只要应用矩形的判定定理，就可以解决这一生产和生活中的问题。最近我们学习的“中心對称图形——平行四边形”一章中，有很多这样的例子。

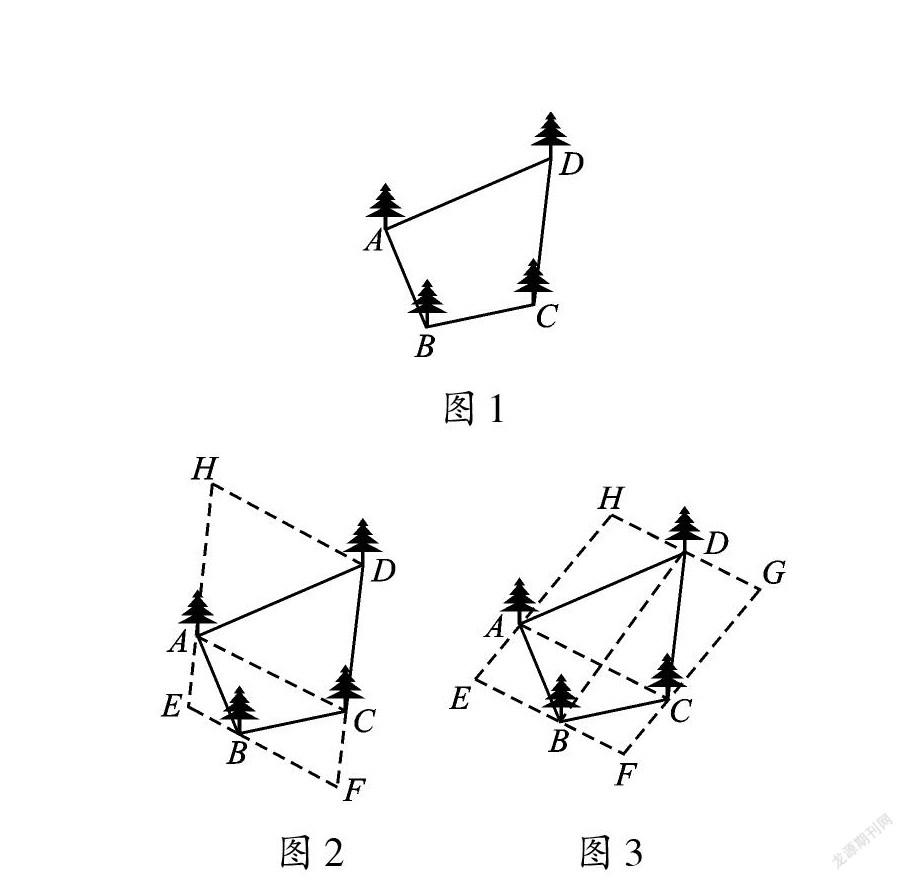
例1 如图1，李村有一个四边形的池塘，在它的四个顶点A、B、C、D处均有一棵桃树。李村准备挖开池塘建养鱼池，要想使池塘面积扩大一倍，又想保持桃树不动，并要求扩建后的池塘形状为平行四边形，请问该村能否实现这一设想？若能，请画出图形并说明理由;若不能，也请说明理由。

【分析】本题考查了平行四边形的判定定理。

解：能实现这一设想，有多种方案，答案不唯一。

方案一：如图2，连接AC，过点D作DH//AC，且使DH=AC，连接HA，过点B作AC的平行线，延长HA、DC，分别交过点B且平行于AC的直线于点E、F，则▱EFDH即为扩建后的平行四边形。

方案二：如图3，连接AC、BD，分别过点B、D作AC的平行线，分别过点A、C作BD的平行线，这两组平行线的交点分别为点E、F、G、H，则▱EFGH即为扩建后的平行四边形。

例2 图4为某城市部分街道示意图，四边形ABCD为正方形，点G在对角线BD上，GE⊥CD，GF⊥BC，AD=1500m。小敏行走的路线为B→A→G→E，小聪行走的路线为B→A→D→E→F。若小敏行走的路程为3100m，则小聪行走的路程为________m。

【分析】本题考查了正方形的性质、矩形的性质、等腰三角形的性质及全等三角形的性质和判定。解决本题的关键是证明AG=EF，DE=GE，并理解小敏与小聪路程差的意义。

解：如图5，连接GC。

∵四边形ABCD为正方形，

∴AD=DC，∠ADB=∠CDB=45°。

∵∠CDB=45°，GE⊥DC，

∴△DEG是等腰直角三角形，

∴DE=GE。

易证△AGD≌△GDC，

∴AG=CG。

在矩形GECF中，EF=CG，

∴EF=AG。

∵BA+AD+DE+EF-BA-AG-GE=AD=1500m，

又∵小敏共走了3100m，

∴小聪行走的路程为3100+1500=4600（m）。

同学们，数学和生活是一对形影不离的好朋友，当我们遇到生活问题时，不妨想一下能否从数学的角度思考。只要我们勤动脑，多努力，就会感受到数学的无穷魅力。

（作者单位：江苏省常州市同济中学）