妙用“特殊与一般”， 学好“平行四边形”

张伟俊

“从特殊到一般，再由一般到特殊”是人类认识世界的基本过程，也是一种重要的数学思想方法。在数学学习的过程中，我们常常需要处理特殊与一般的关系，从特殊到一般，或是从一般到特殊，这就形成了数学的两种基本方法：一般化和特殊化。“中心对称图形——平行四边形”这一章中，蕴含了很多特殊与一般的关系。我们如果能用好这种关系，必将达到事半功倍的学习效果。

一、特殊化：从一般到特殊

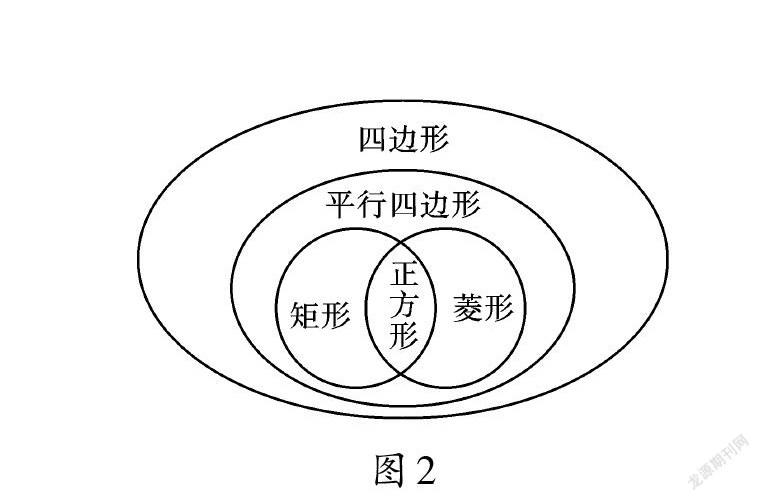
在本章的学习中，无论是从旋转到中心对称，还是从平行四边形到矩形、菱形、正方形，都体现了特殊化的思想。初学时，有些同学看到这么多图形，每种图形还有很多性质，不太容易记住，甚至感到混乱。其实，如果我们以特殊化的方法来构建“平行四边形”的知识结构体系，便能很快分清哪个图形具备什么性质了。如图1所示，在四边形的基础上，再有“两组对边分别平行”，便得到平行四边形;在平行四边形的基础上，再有“一个角是直角”，便得到矩形，或再有“一组邻边相等”，便得到菱形，而同时具备“一个角是直角”和“一组邻边相等”的条件便成了正方形。也就是说，平行四边形是特殊的四边形，矩形、菱形、正方形都是特殊的平行四边形，同时，正方形还是特殊的矩形、特殊的菱形。从这个角度，我们又可以用图2来描述它们之间的关系。

在这两幅结构图中，一般图形的性质，是各个特殊图形的共性。例如，所有平行四边形（包括矩形、菱形、正方形）都具有“对边平行且相等”“对角相等”“对角线互相平分”等性质。特殊图形存在于一般图形之中，特殊图形不仅具有一般图形的共性，而且还有自己的特性。例如，矩形不仅具有平行四边形的所有性质，而且还有“四个角都是直角”“两条对角线相等”等特性，菱形也有“四边相等”“对角线互相垂直”等特性，这些特性并非所有平行四边形都具有。一般地，图形越特殊，它具有的特性也会越多。因此，我们在学习中可以从“图形在特殊化的过程中增加了哪些特性”的角度，去把握各种图形所具有的特性。

除此以外，在解决问题的过程中，我们也常常运用特殊化的方法来解决一般性的问题，尤其是在从一般性的角度找不到方法或者不易解决的时候。

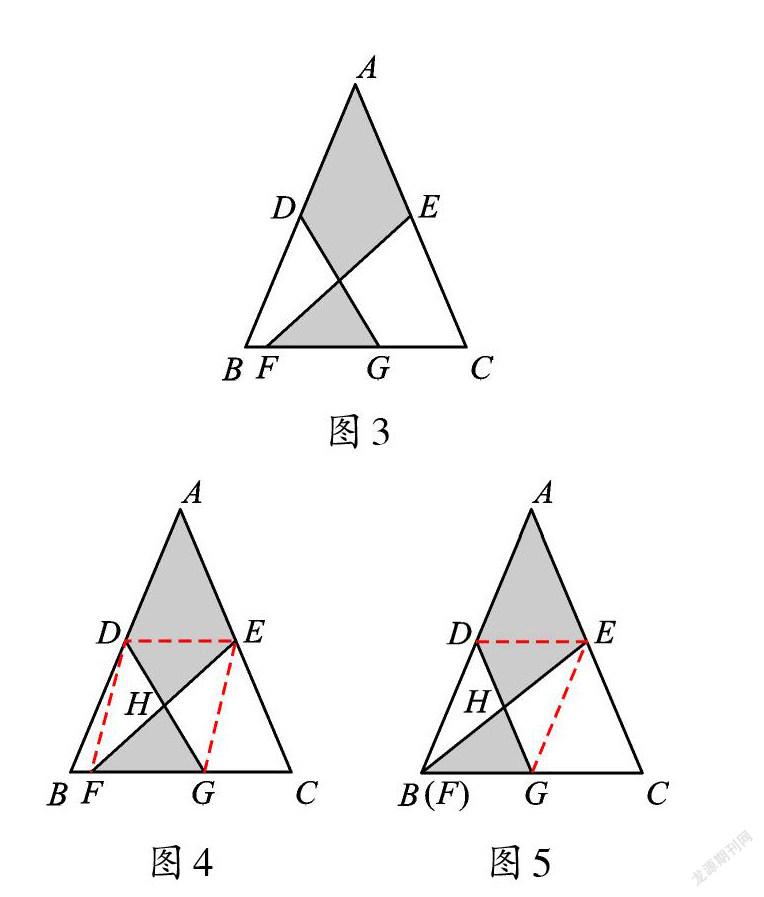
例1 如图3，在△ABC中，AB=AC=13，BC=10，D、E分别是AB、AC的中点，F、G为BC上的点，且FG=5，连接DG、EF，则图中阴影部分的面积为               。

【分析】由“D、E分别是AB、AC的中点”，可知DE是△ABC的中位线，于是便可推得DE∥FG且DE=FG。如图4，连接DE、DF、EG，可得四边形DFGE为平行四边形，所以S△FGH=S△DFH，故图中阴影部分的面积可转化为△ADE与△FDE的面积之和。又因为DE∥FG，所以无论F点位于BC边上的何处，△FDE的面积都是不变的。因此，可以寻求F点的特殊位置，求解出此题的答案。譬如，假设点F与点B重合（如图5），此时图中阴影部分的面积便转化成了△ABE的面积，即为△ABC的面积的一半，等于30。当然，这样的问题也可以从一般性的角度解决。请同学们思考一下，从一般性的角度，解决本题还需要说明什么？

二、一般化：从特殊到一般

与上述过程相反，有的时候，我们也需要从特殊到一般，从特殊情况入手，去探求一般规律，以便更好地解决特殊问题。如苏科版数学八年级下册第87页的例题。

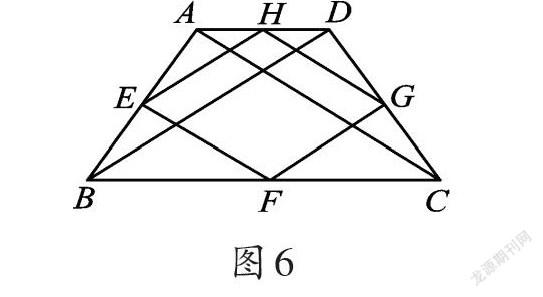
例2 已知：如图6，在四边形ABCD中，AC=BD，E、F、G、H分别是AB、BC、CD、DA的中点。求证：四边形EFGH是菱形。（详解见教材。）

图6中的四边形EFGH可以称为四边形ABCD的中点四边形，四边形ABCD可以称为原四边形。例2证明了当原四边形对角线相等时，它的中点四边形是菱形。

在这个问题解决之后，我们会思考什么问题呢？或许，有的同学会思考：如果原四边形是任意四边形，它的中点四边形还有特殊性吗？还有的同学会思考：如果一个四边形的中点四边形是矩形或者正方形，这个四边形需要满足什么条件呢？这便是从一般化的角度提出的问题，期望从一个特例出发，探索出原四边形与其中点四边形之间关系的一般规律。

如图6，由于“E、F、G、H分别是AB、BC、CD、DA的中点”，构造三角形中位线，根据“三角形的中位线平行于第三边，并且等于第三边的一半”可得EF∥GH且EF=GH，即四边形EFGH为平行四边形。故任意四边形的中点四边形都是平行四边形。在此基础上，要使中点四边形为矩形，需要增加条件“有一个内角为直角”，从而推出需要原四边形的对角线互相垂直;要使中点四边形为正方形，需要增加条件“有一个内角为直角”和“有一组邻边相等”，从而推出需要原四边形的对角线互相垂直且相等。

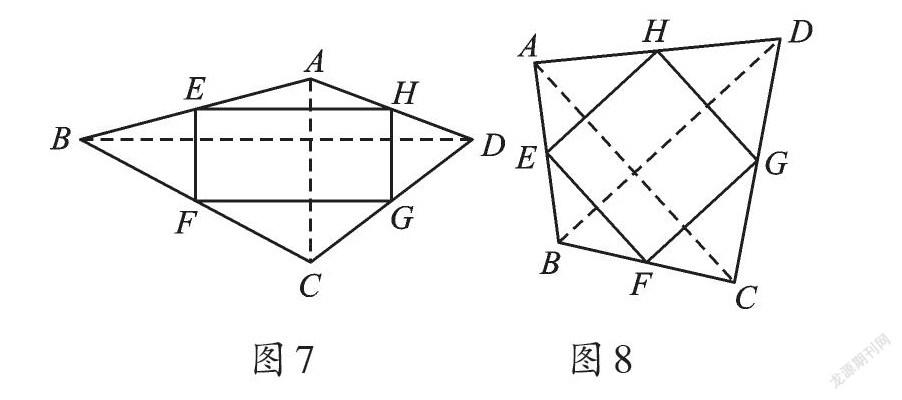
这样便得到了原四边形与其中点四边形之间的一般关系：任意四边形的中点四边形是平行四边形;如图6，对角线相等的四边形的中点四边形是菱形;如图7，对角线互相垂直的四边形的中点四边形是矩形;如图8，对角线互相垂直且相等的中点四边形是正方形。

由此可见，特殊与一般是对立统一的，在一定条件下，它们是可以相互转化的。无论是从特殊到一般，还是从一般到特殊，都是我们发现问题、提出问题的视角，也是我们分析问题、解决问题的方法，需要我们认真领会、准确把握。希望同学们在今后的学习中，能自覺运用特殊与一般的思想方法去思考问题、解决问题。坚持这样做，你的认知水平和思维能力一定会得到长足发展。

（作者单位：江苏省常州市武进区湖塘实验中学）