新“将军饮马”问题
2022-05-27周燕
周燕
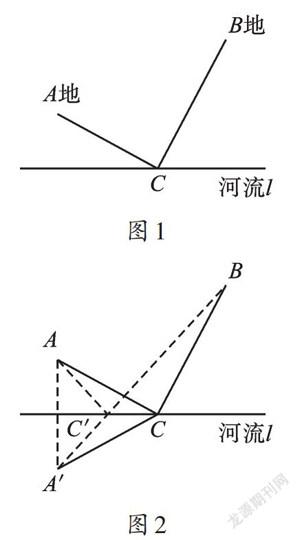
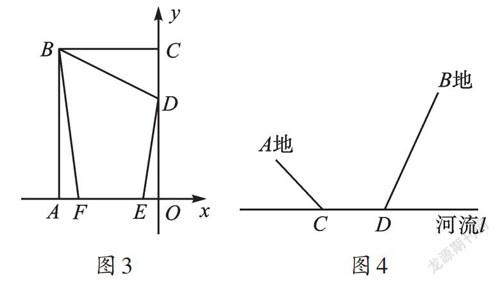
传说古希腊有一位将军向学者海伦提出过一个问题:如图1,从A地出发到河边饮马,然后再走到B地,如何设计一条最短路线?海伦是这样做的:如图2,过点A作关于河岸的对称点A',连接A'B并与河岸线交于点C',从A地出发沿直线走到C'处饮马,之后再由C'沿直线走到B地即为最短路线。这实质上是运用了图形的对称性,因为点A'是点A关于l 的对称点,河流l相当于线段AA'的中垂线,所以AC=A'C,根据两点之间线段最短,A'B为最短路线。这类问题在中考中时常出现,但下面两道题有别于普通的“将军饮马”问题,你还能顺利解决吗?
一、新“将军饮马”——河畔踱步
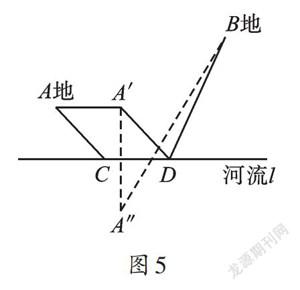
例1 (2021·山东聊城)如图3,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴上,B、D两点坐标分别为B(-4,6)、D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF周长最小时,点E的坐标为_______________。
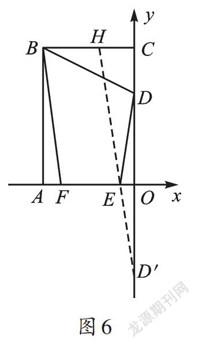
【场景再现】如图4,如果这匹马在C处喝完水后沿着河岸线再走一段固定的距离,你还能找到最短路线吗?即CD的长为定值,求AC+BD的最小值。比起“将军饮马”问题,这两条线段被隔开了一段距离,要是没有这段距离该多好啊。你有办法将他们“复位”吗?我们可以将线段AC沿着河岸线向右平移至A'D,使得C、D两点重合。因为平移不改变线段的长度,所以A'D+BD=AC+BD,此时过点A'作河流l的对称点A″,连接A″B即可(如图5)。
【思路分析】要研究四边形BDEF周长的最小值,其实就是要研究BF+DE的最小值。而本题中的B、D两点就是以上场景中的A、B两地,EF则是马沿着河岸走過的距离。根据以上分析,在BC上截取BH=3,如图6,可得四边形BHEF是平行四边形,并将BF转化为EH。作点D关于x轴的对称点D',连接D'H交AO于点E,当E、H、D'三点共线时,EH+D'E有最小值,利用点D(0,-4)、H(-1,6)可求得直线D'H的表达式为y=-10x-4。当y=0时,x=-0.4,即点E的坐标为(-0.4,0)。
二、新“将军饮马”——河间游走
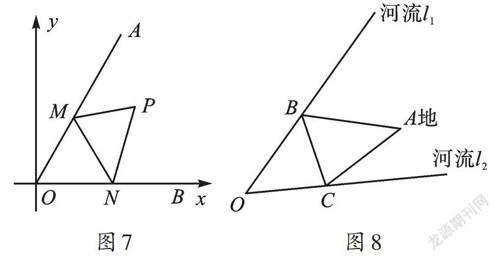
例2 (2020·湖南永州)如图7,∠AOB=60°,在∠AOB内有一点P(4,3),M、N分别是OA、OB边上的动点,连接PM、PN、MN,则△PMN周长的最小值是_______________。
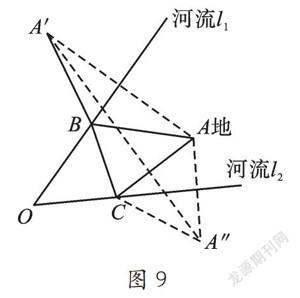
【场景再现】如图8,这次马从A地出发先去河流l1的B处喝水,再跑去河流l2的C处喝水,最终回到A地,你能设计出最短行走路线吗?我们可以将两次喝水路线分开研究,发现无论是AB+BC还是BC+CA都符合“将军饮马”结构。因此,过点A分别作关于l1与l2的对称点A'、A″,如图9,根据中垂线的性质,马的行走路线长即A'B+BC+CA″的值,根据两点之间线段最短可得A'A″即为最短路线。
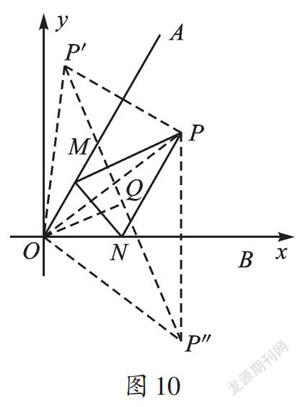
【思路分析】本题中的点P即为以上场景中的A地,OA、OB为那两条河,△PMN的周长为马的行走路线。根据以上分析,分别作点P关于射线OA、射线OB的对称点P′与点P″,连接P′P″,与OA、OB分别交于M、N两点,如图10,此时△PMN周长最小,最小值为P′P″的长。连接OP′、OP″、OP,利用垂直平分线的性质与点P坐标(4,3)得到OP′=OP″=OP=5,且∠POA=∠P′OA,∠POB=∠P″OB。又因为∠AOB=∠AOP+∠BOP=60°,所以∠P′OP″=120°。根据三角函数相关知识可求得△PMN周长的最小值是[53]。
(作者单位:江苏省泰州市海军中学)
