MATLAB 在常微分方程课程教学中的应用

李 政，李希敏

（桂林师范高等专科学校数学与计算机技术系，广西桂林 541199）

常微分方程课程是大学数学等相关专业的核心课程，其应用领域十分广泛，很多与变化率相关的问题都可以用微分方程来解决。如：鱼的捕捞、传染病的传播预测、人口增长的预测等[1]。在实际的课程教学中存在几个急需解决的问题：一是很多的方程求解步骤烦琐冗长，得到的解复杂，无法了解解的性质；二是大部分方程可以证明其有解，却无法求出精确的解，需要求方程的数值解，而数值解的计算量大，无法在课堂上完成，影响教学的完整性；三是绘制向量场是求方程近似解与研究方程解的性质的重要手段，但是向量场的绘制计算量大，手工绘制的向量场误差大，影响了对解的研究。本文以MATLAB 为工具，切实解决常微分方程课程教学中存在的这些问题。

一、MATLAB 的特点

MATLAB 是世界著名的数学软件之一，它在符号运算与数值计算方面功能强大。MATLAB 可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于科学计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。矩阵是MATLAB 的基本数据单位，其指令表达式与数学、工程中常用的形式十分相似，用MATLAB 来解数学问题要比用C、FORTRAN 等语言完成相同的事情简单方便，MATLAB 同时吸收了像Maple 等软件的优点，成为一个强大的数学软件。

二、利用MATLAB 求微分方程的解析解并绘制积分曲线

很多微分方程的求解过程十分冗长，同时需要进行各种复杂的变换处理，给微分方程的应用带来很大的麻烦，耗费了教师大量的课堂时间。利用MATLAB 可以快速求出方程的解析解，同时绘制积分曲线，便于对解的情况进行研究。

例1：求微分方程的特解，并画出积分曲线。

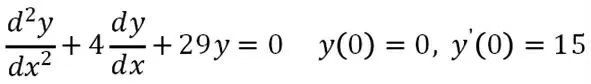
分析：在MATLAB 中可以调用函数dsolve（）求微分方程的通解和特解，其调用的一般格式为：dsolve（＇eq1，eq2…＇，＇cond1，cond2，…＇）。用fplot（）函数来绘制积分曲线图，其调用格式为fplot（f，xinterval）。其中用Dy，D2y 分别表示y 的一阶导数与二阶导数。MATLAB 求解的步骤如下：

syms x y；%定义x，y 为符号变量（便于求导）；y＝dsolve（＇D2y＋4*Dy＋29*y＝0＇，＇y（0）＝0＇，＇Dy（0）＝15＇，＇x＇）；%求解此微分方程在初始条件下的特解，得到结果如下：

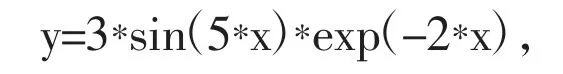
这里exp 是常数e，再调用fplot（）绘制函数图像[2]：

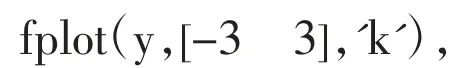
得到积分曲线如图1 所示。

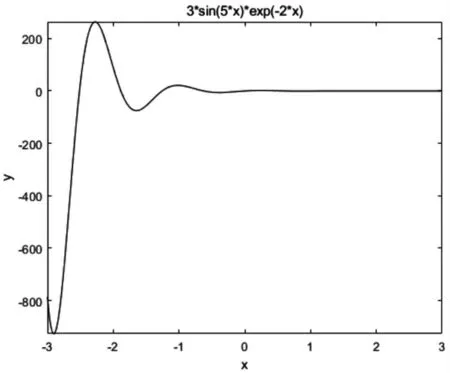
图1 方程的积分曲线

整个求解过程简单快速，并能精确地绘制出积分曲线，便于分析研究解的情况，节省大量的时间，可以提高课堂效率。

三、利用MATLAB 求微分方程的数值解

（一）微分方程的数值解的定义

设y（x）是初值问题的解：

y（x）的存在区间是[a，b]，令a＝x0＜x1＜x2＜…xn＝b，hk＝xk＋1-xk且h＝（b-a）／n，把h 称为步长。假定y（x）的表达式很难求得，但是可以利用数值方法求得y（x）在点xk的值y（xk）的近似值，记为yk，也就是y（xk）≈yk，从而求得一组点集：（x1，y1），（x2，y2）…（xn，yn），称为微分方程的数值解。

（二）欧拉折线法求微分方程的数值解

欧拉折线法的核心是利用差分来近似微分，简单地说是以直代曲，在很小的局部把曲线看成直线。根据欧拉折线法可以得到方程的数值解：

设节点为a＝x0＜x1…xn＝b，初值问题欧拉折线法为：

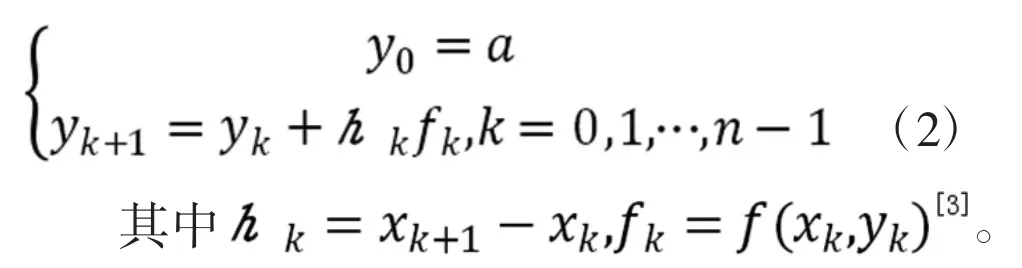
分析：可以看到，例2 的初值问题是无法找到方程的解析解的，利用欧拉折线在MATLAB中实现求方程的数值解如下：

可以看到，利用MATLAB 能快速求出微分方程的数值解，并绘制数值解的散点图（见图2），从而观察到解的大致图像。但是，在这里要注意：一般数值解的范围比较小（在这里我们设定的间是［1，1.4］），否则误差会比较大。

图2 方程数值解的散点

四、利用MATLAB绘制微分方程的向量场

通过向量场可以近似积分曲线，还可根据向量场本身的性质来研究解的性质，它是微分方程课堂教学中的重点内容，可是在教学过程中向量场的绘制往往占用教师很多的时间。如果向量场中向量的绘制数量太少，就会看不到积分曲线的性质与特征，这时可以利用MATLAB 绘制向量场，提高课程教学的效率。

分析：定义一个生成向量场数据的函数：

利用MATLAB 的quiver 函数绘制向量场，quiver 调用格式：quiver（X，Y，U，V）在由X和Y 指定的笛卡尔坐标上绘制具有定向分量U 和V 的箭头。

绘制向量场过程如下：

结果如图3 所示：

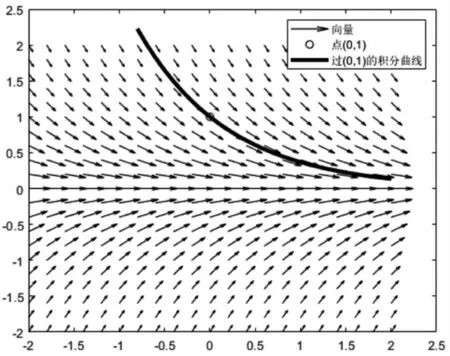
图3 向量场与积分曲线

通过向量场与积分曲线的对比，可以看到向量场近似方程的解，从而加深学生对向量场与积分曲线之间关系的了解，突出教学重点，提高课堂教学的效率。

五、结语

把MATLAB 强大的符号运算能力、精确的数值计算与丰富的绘图功能应用到常微分方程的课堂教学中，解决教学中求方程的解析解难、求数值解计算量大、绘制向量场不精确等问题，可以提高常微分方程课堂教学效率，促进微分方程在实际中的应用。