测量条件对A/D动态有效位数评价的影响

2022-05-26梁志国

计量学报 2022年4期

梁志国

(北京长城计量测试技术研究所计量与校准技术重点实验室,北京 100095)

1 引言

动态有效位数是A/D转换器的一项重要指标,用于表征其动态测量总体误差,也常被用于评价以A/D转换为核心的数字化测量仪器和设备的动态特性。例如,数据采集系统、数字波形记录仪、瞬态记录仪、数字示波器等[1～4]。

关于动态有效位数的测量评价,有多种不同的方式方法。从信号源角度,有三角波激励法和正弦波激励法;从数据处理方法角度,有波形拟合法、直方图统计分析法、频谱分析法、失真测量法等多种方法[5～19],均可以获得动态有效位数的评价结果。而其中应用最广、影响力最大的是正弦波激励下的波形拟合法,业已被列入多个标准文件中,作为推荐性评价方法。

与其它许多指标特性不同,动态有效位数虽然具有一定的稳定性和规律性,仍然被认为是一种条件参数指标。即,伴随着测量条件的不同会有所不同。因而,通常的A/D转换器或数字示波器等在给出动态有效位数的指标参数时,总会伴随着其测量条件,如信号频率及幅度值。实际上的测量条件则远不止这些,其它如初始相位、直流分量,以及采集速率、波形序列长度、波形序列所包含的信号周波数等的影响如何,以及这些条件变化时,对动态有效位数及评价误差的影响有多大,均无明确结论。唯一有明确结论的规律是伴随着信号频率的增加,动态有效位数评价结果会呈单调下降的趋势。

本文后续内容,将对正弦信号激励下,上述测量条件及变化给动态有效位数带来的测量误差变化进行仿真研究,并试图获得明确可用的定量结论。

2 基本思想及条件设定

2.1 基本思想

A/D量化误差是一种有确定模型的系统误差,作为量化误差一种动态表征形式的动态有效位数也应该如此。而正弦波形在值域里是一种非等概率密度函数波形,其量化后的峰值码和谷值码出现的概率远大于其它部分量值量化码出现的概率。因而,测量条件变动时,其有限长序列样本点的时间分布特性和统计特性均会产生变化。相应地,以正弦激励进行测量时,信号幅度变化,将对幅度范围内是否包含整数个量化误差区间以及区间分布产生影响；在幅度确定后,直流分量的变化,也将对幅度范围内量化误差区间及分布产生影响,从而影响动态有效位数的评价结果。

另外,样本序列的长度,以及序列内所包含的信号周波数的变化是否会影响有效位数的评价,均需要研究确定。基于此,选取上述可能会带来影响的测量条件作为研究对象,选取有效位数误差作为指标参数,以仿真理想数据方式,在各个测量条件分别变化时,考察动态有效位数误差的变化情况。

正弦波采样测量中,采样速率与信号频率是关联量,两者之比是每个周波的采样点数,通过选择不同的采样速率可改变该比值；当采样速率固定后,采样序列的长短决定了其所包含周波数的多少。通过选取量程范围,改变被测信号幅度与量程的占比；通过选择不同A/D位数的测量仪器和系统,改变量化误差。最终,改变正弦波拟合参数的误差界。

关于正弦拟合,在大多数应用中,其采样序列长度在几十点到几千点之间,序列所含的信号周波数为几个至十几个周波。所用的采样系统A/D位数主要有8、12、16、24 bit等几种。

在序列长度变化过程中,其它信号参数如幅度、直流分量、相位等也将处于变化之中,它们共同作用的结果,将揭示拟合误差的实际变化情况。

2.2 仿真条件和指针设定

综合考虑各方面因素,选出具有相互独立性和系统完备性的左右动态有效位数测量误差的测量条件为:

1)A/D位数,用于确定量化水平及影响,并提供动态有效位数的额定标准值；

2)采样序列包含周波数,确定周波数的影响；

3)采样序列长度,即序列包含的样本点数,确定采样序列长度的影响；

4)信号幅度,确定幅度变动的影响；

5)初始相位,确定信号相位变化带来的影响；

6)直流分量,确定直流分量变化带来的影响。

经过四参数正弦曲线拟合后,获得动态有效位数的误差界,以Bit表述；有效位数通常用以表述拟合曲线和实际测量序列之间的拟合残差,假定其在整个信号量程范围内均匀分布,按照纯量化误差规律折合成的A/D位数[17]；理想状况下,有效位数的量值应该与测量序列所用的A/D位数相等。它的误差界,应该是有效位数不确定度的波动边界。

LSB(least Bit)称为A/D的最小量化阶梯。

2.3 误差界搜索

动态有效位数的误差界,是在上述6项测量条件下,固定其中的5项,变化1项,搜索出该条件变化时,四参数正弦拟合所获得的动态有效位数指标的误差界。

在考察序列长度的影响时,则主要变化序列长度,辅助调整变化其它测量条件,着重分析出序列长度作为主导因素时,给动态有效位数指标的拟合误差带来的影响规律。

3 仿真实验及数据处理

使用计算机按照数学关系产生理想正弦数据,以仿真A/D位数进行量化,生成理想仿真序列。将该具有已知参量的仿真序列在选定的正弦波拟合软件中进行数据处理,获得拟合参数。

令仿真参数按照已知规律变化,获得变化条件下的拟合参数变化规律,并以此搜索动态有效位数的误差界。

3.1 仿真实验条件

为方便参数调控,不失一般性,设定包含6项测量条件的仿真实验条件如下:

1)A/D位数,基本参量为8 bit；

2)采样序列包含周波数,未特别说明时,为20个周波；作为主变化因素时,变化范围为0.90～21.00个周波；0.01周波步进；作为辅助变化量时,变化范围为1～20个周波；1周波步进；

实际仿真过程中,通过使用归一化频率1 Hz来调整采样速率,结合样本点数,最终构建周波数；

3)序列样本点数,未特别说明时,序列样本点数为16 000点；

作为主变化因素时,变化范围为100～16 000点；1点步进；作为辅助变化量时,变化范围为1 000～16 000点；1 000点步进；

4)信号幅度,使用归一化幅度1；未特别说明时,幅度为82.031 25%(量程；并以此设定量程范围；

作为主变化因素时,幅度宏观变化范围为量程的7.8%～100%,0.005 LSB步进；

作为辅助变化量时,在82.031 25%(量程点处,其微观变化范围-0.5～0.5 LSB,0.05 LSB步进；

5)初始相位,未特别说明时,初始相位为0°；作为主变化因素时,变化范围为-180°～180°,1°步进；作为辅助变化量时,范围不变,10°步进；

6)直流分量,未特别说明时,直流分量为0；

作为主变化因素时,变化范围为-1～1 LSB；0.01 LSB步进；

作为辅助变化量时,变化范围为-0.5～0.5 LSB；0.05 LSB步进。

3.2 仿真实验结果及分析

按照上述仿真条件,获得如图1～图20所述的随着不同条件而变化的动态有效位数误差曲线波形。

图1 幅度与周波数变化时的有效位数误差

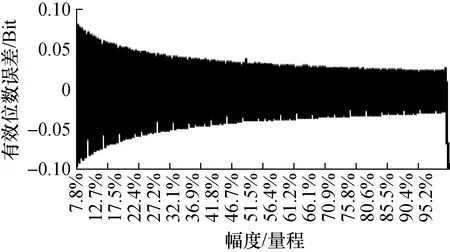
图2 幅度与相位变化时的有效位数误差

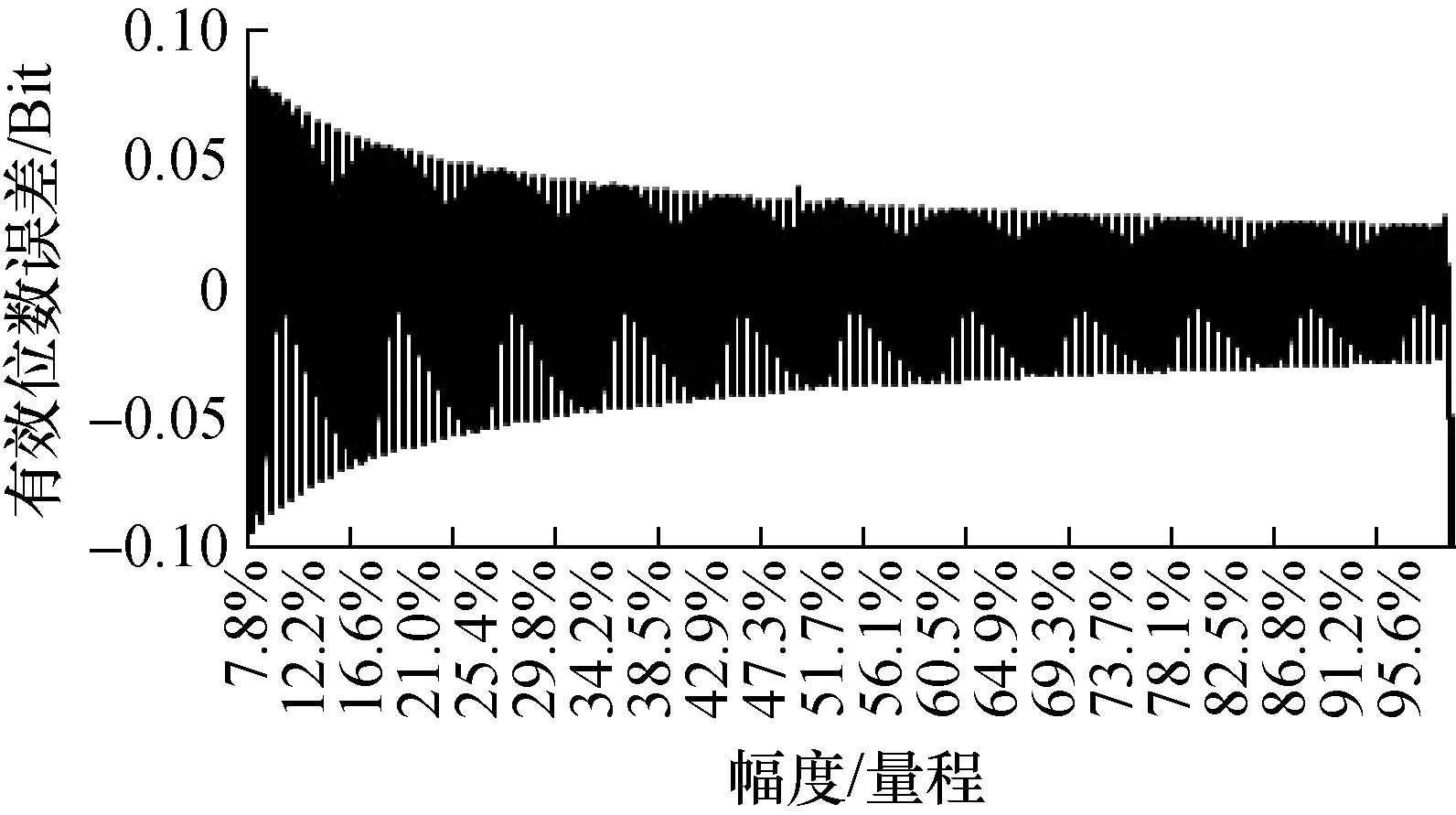
图3 幅度与直流分量变化时的有效位数误差

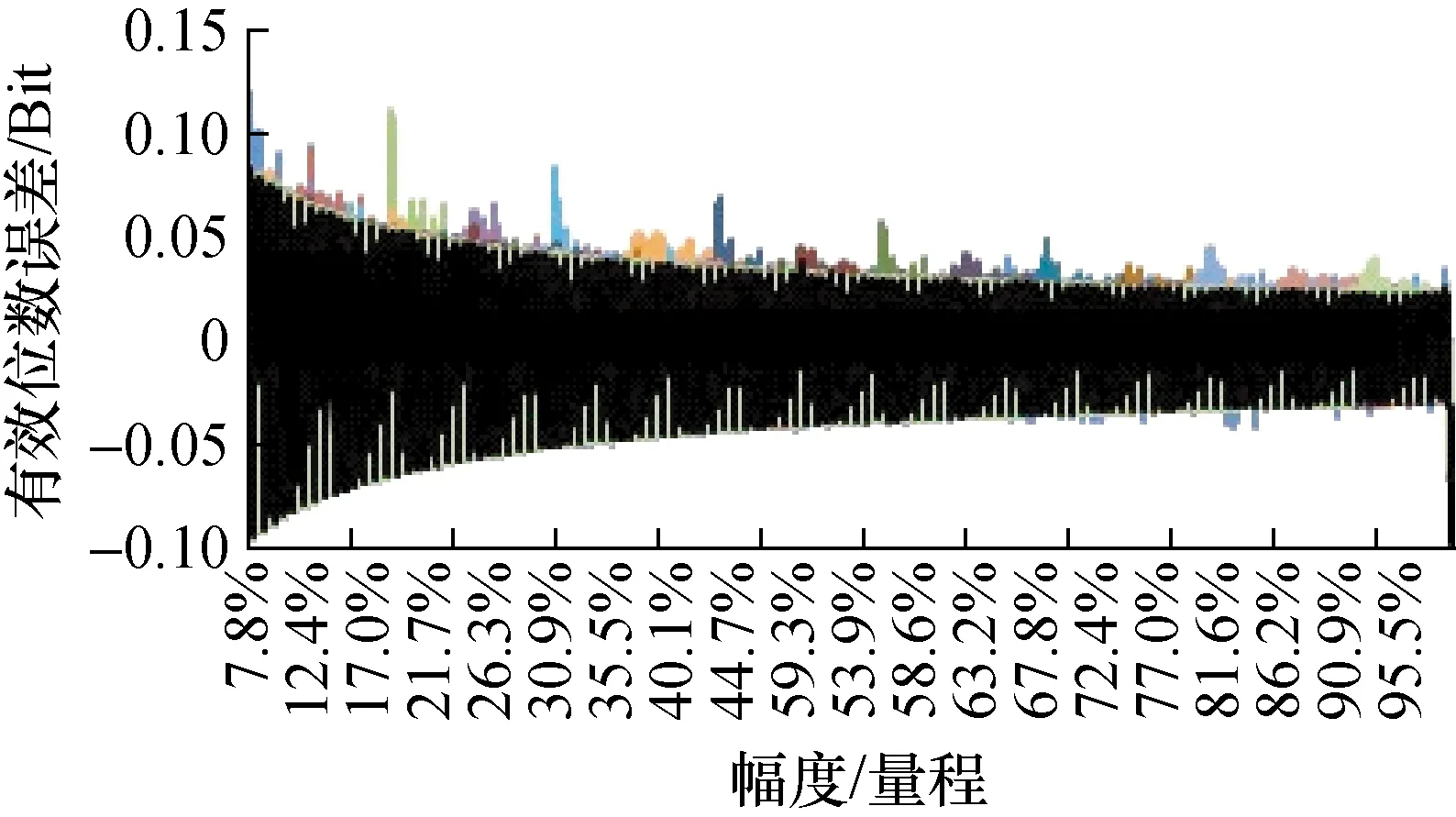
图4 幅度与序列长度变化时有效位数误差

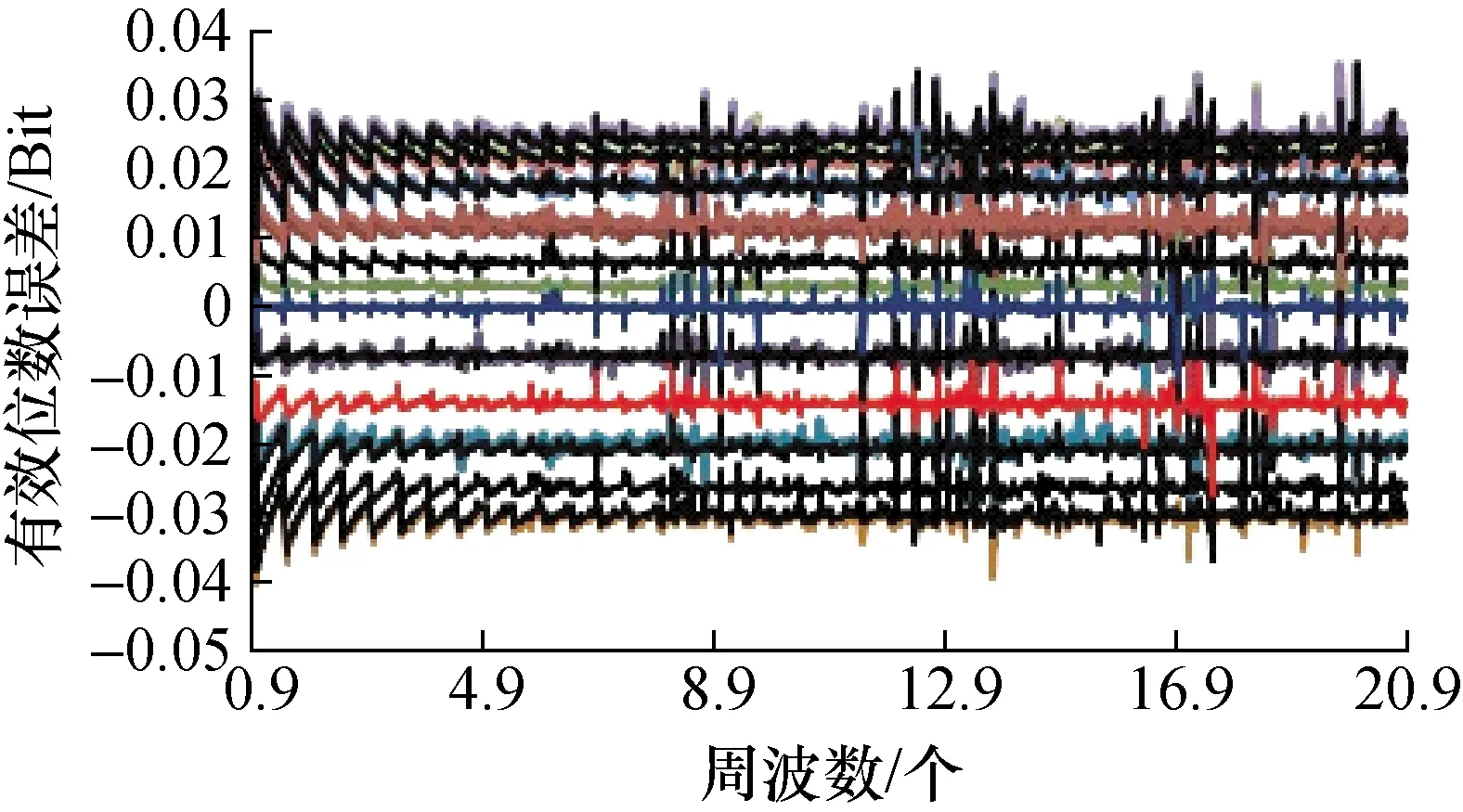
图5 周波数与幅度变化时的有效位数误差

图6 周波数与相位变化时的有效位数误差

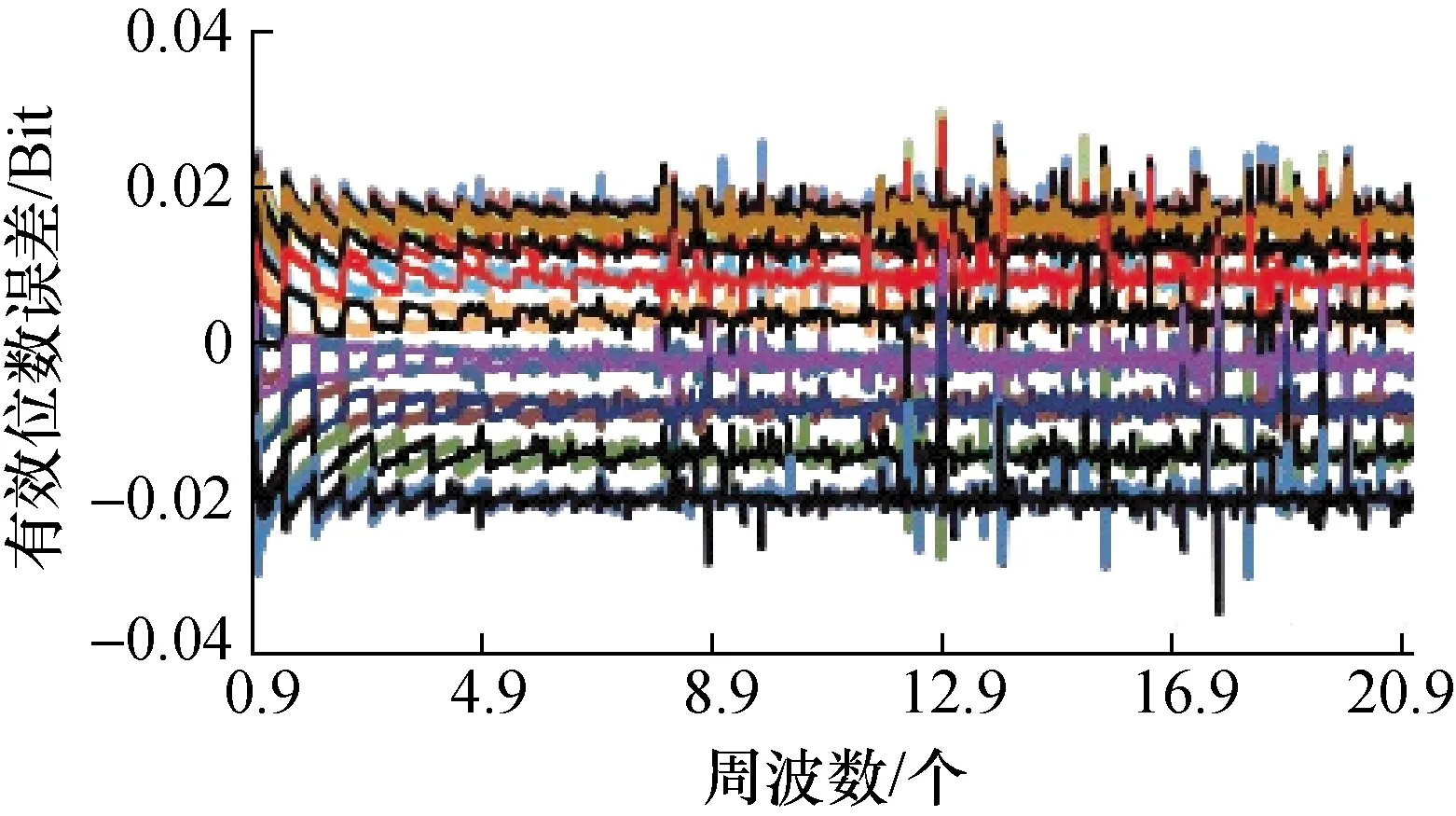
图7 周波数与直流分量变化时有效位数误差

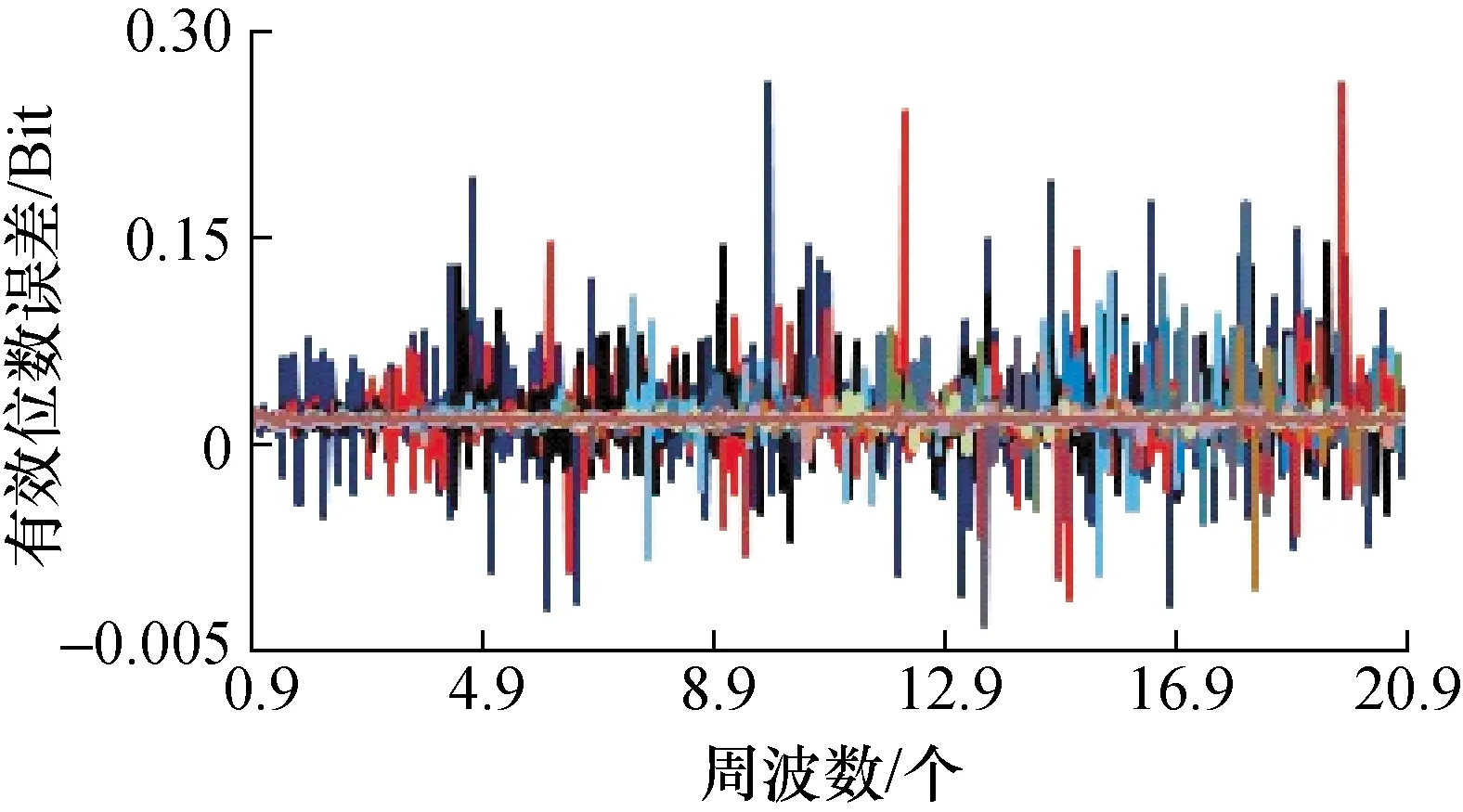
图8 周波数与数据点数变化时有效位数误差

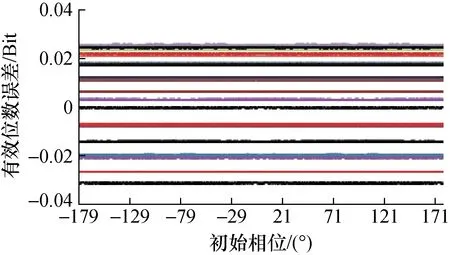
图9 初相位与幅度变化时有效位数误差

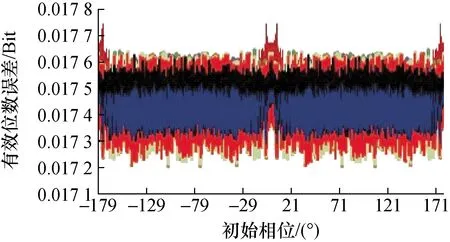
图10 初相位与周波数变化时有效位数误差

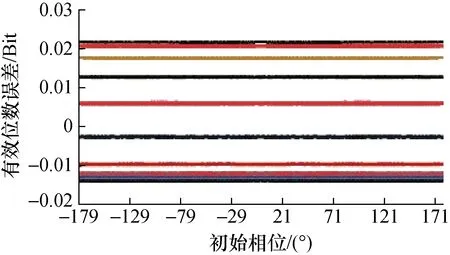
图11 初相位与直流分量变化时有效位数误差

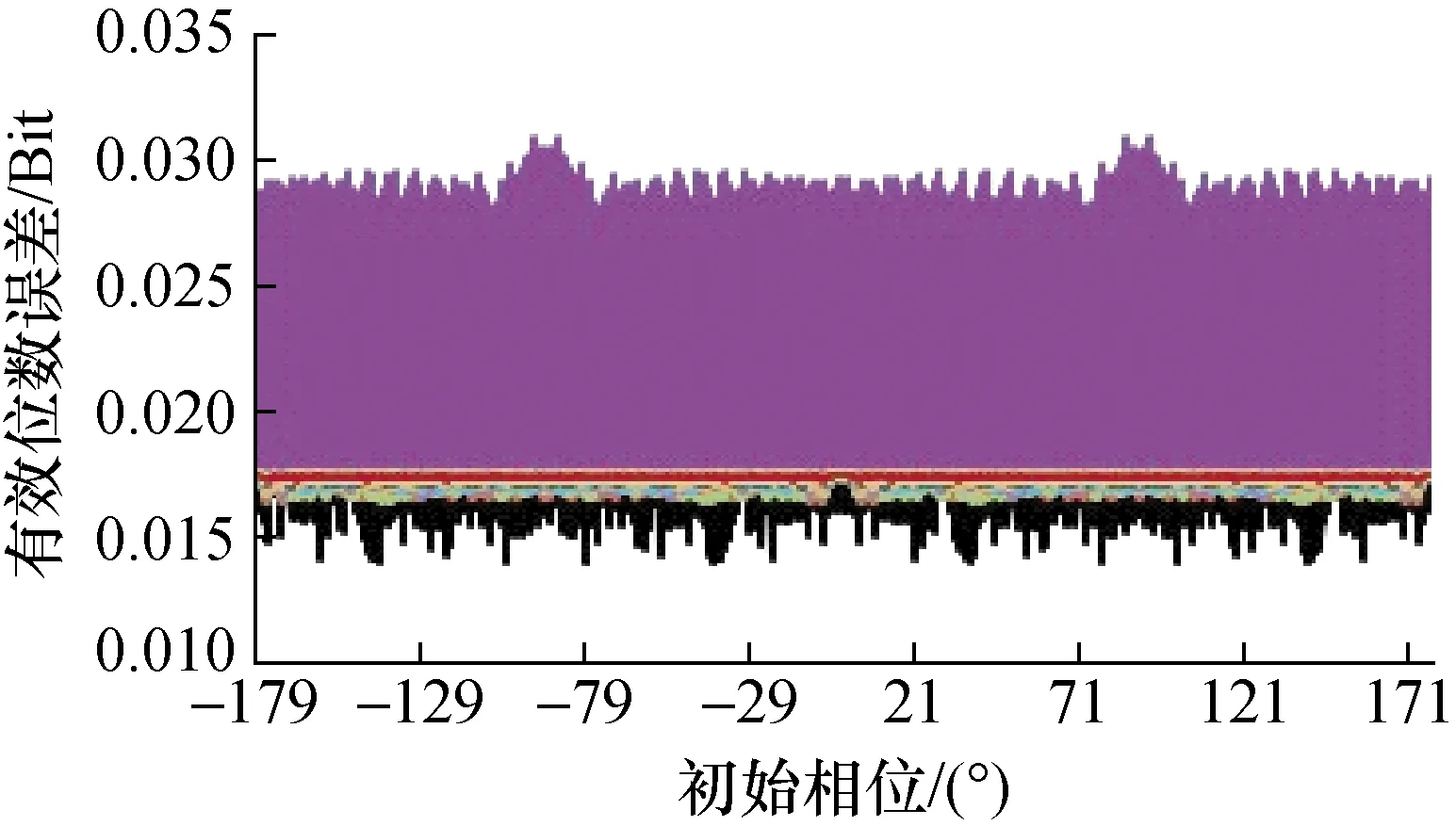
图12 初相位与数据点数变化时有效位数误差

图13 直流分量与幅度变化时有效位数误差

图14 直流分量与周波数变化时有效位数误差

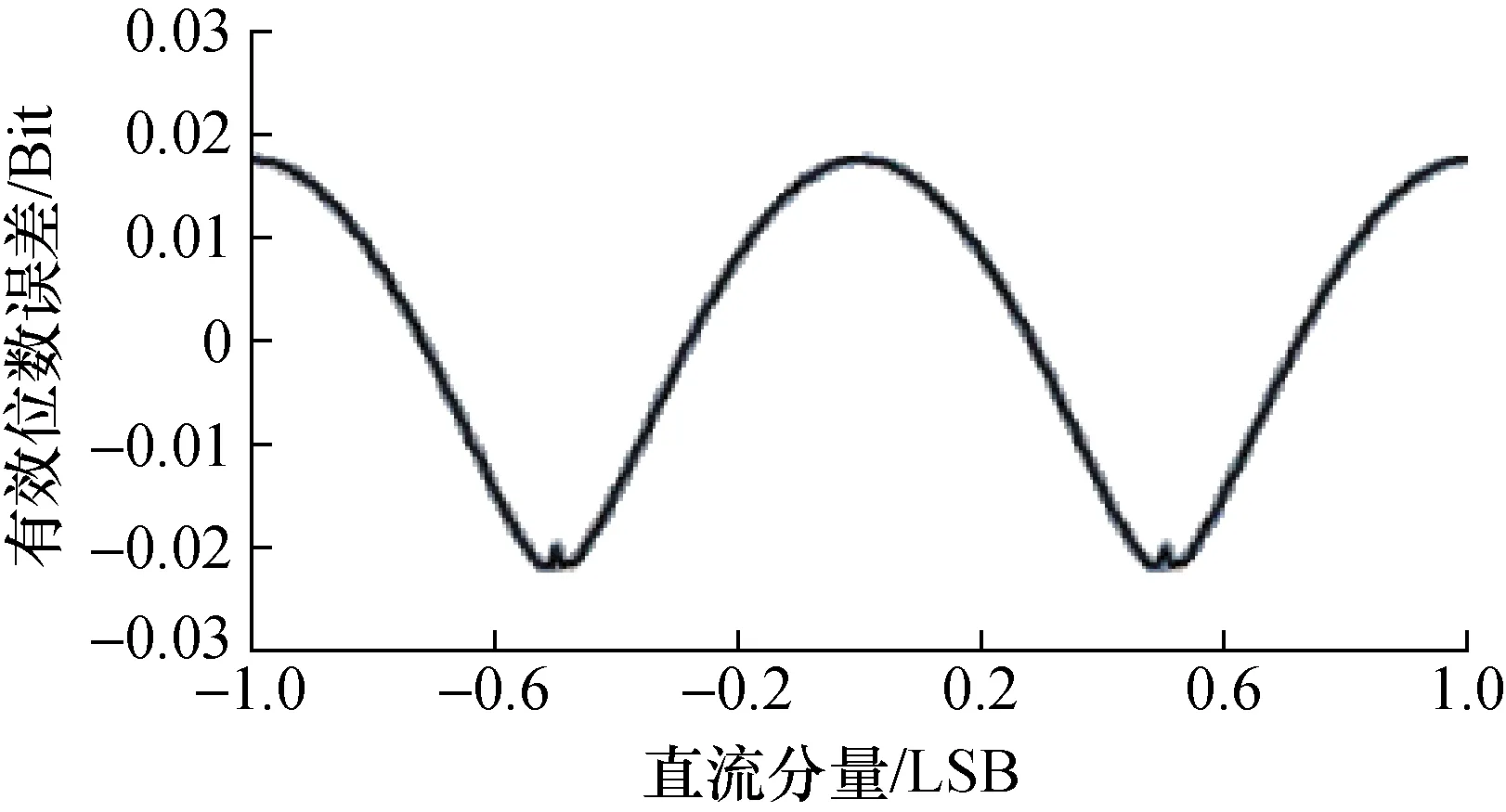
图15 直流分量与初相位变化时有效位数误差

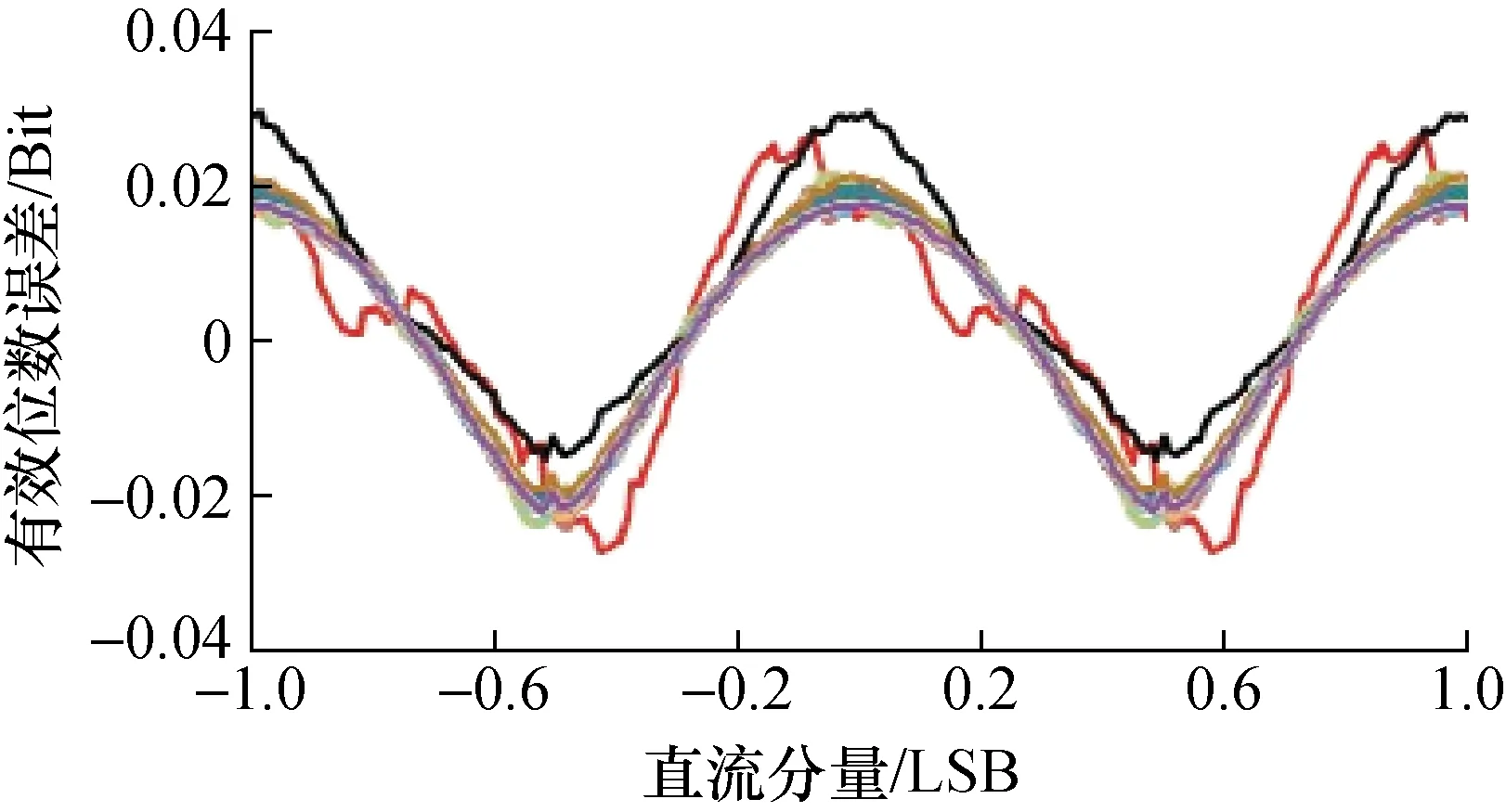
图16 直流分量与数据点数变化时有效位数误差

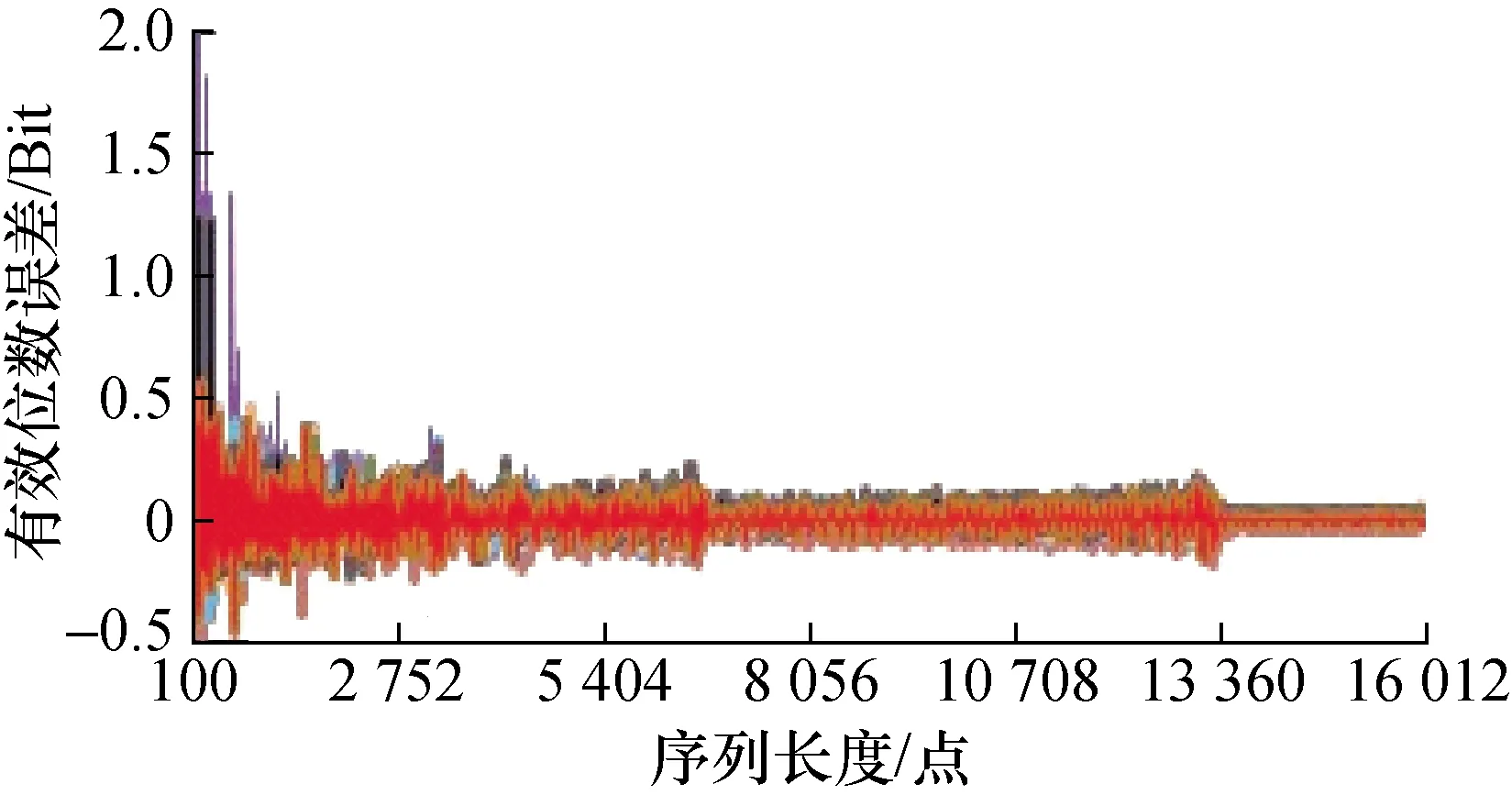
图17 数据点数与幅度变化时有效位数误差

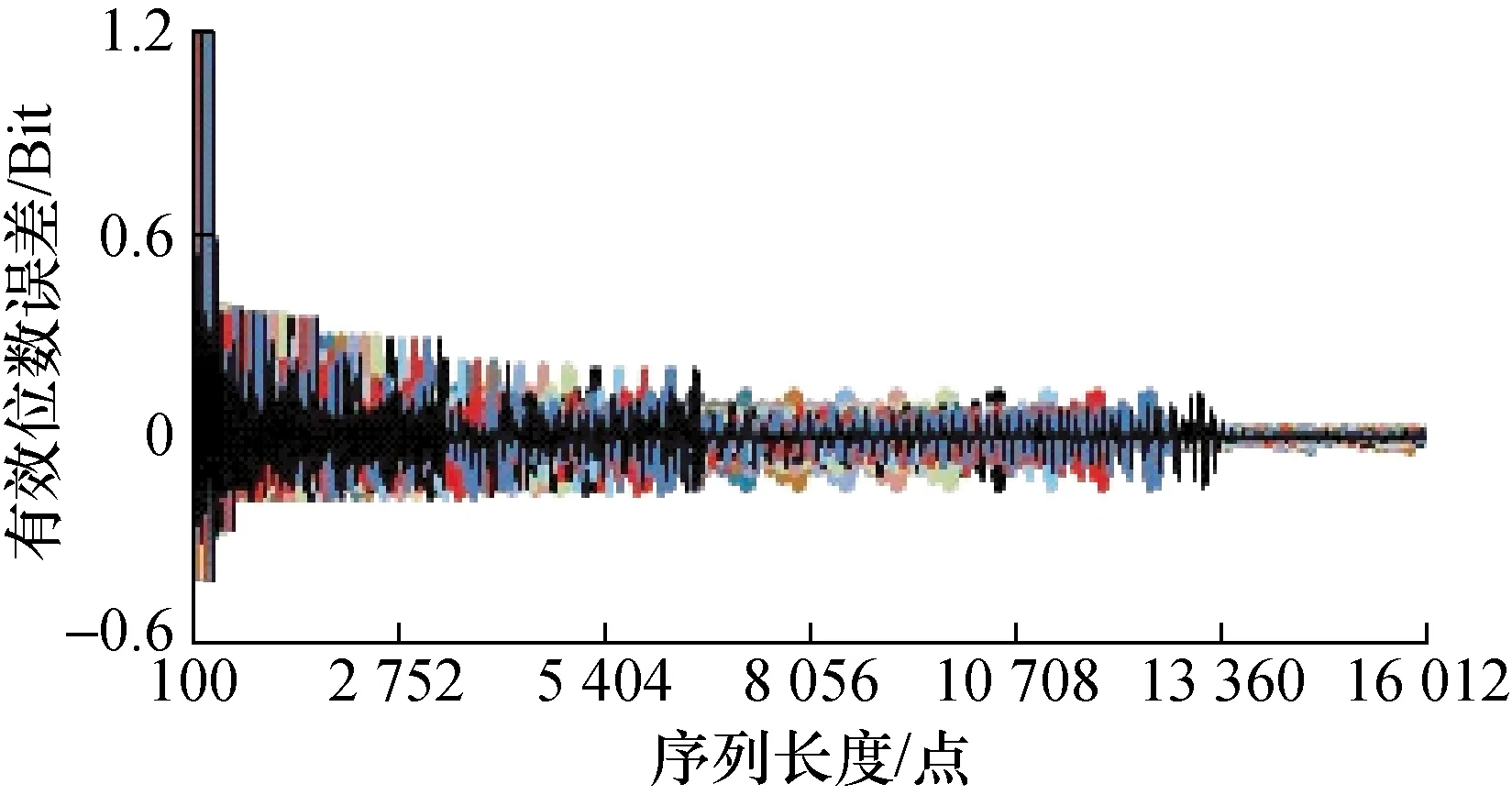
图18 数据点数与周波变化时有效位数误差

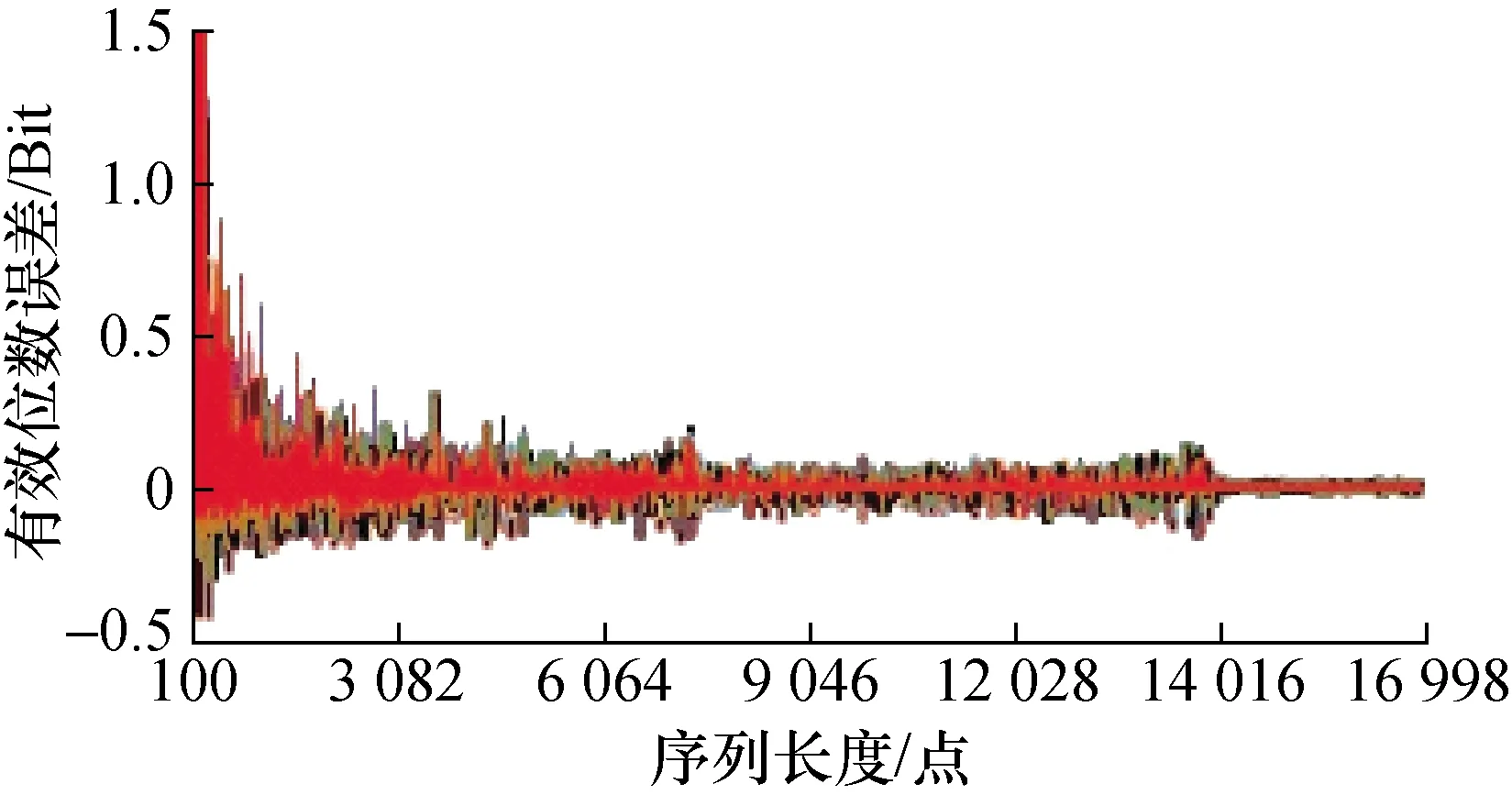
图19 数据点数与初相位变化时有效位数误差

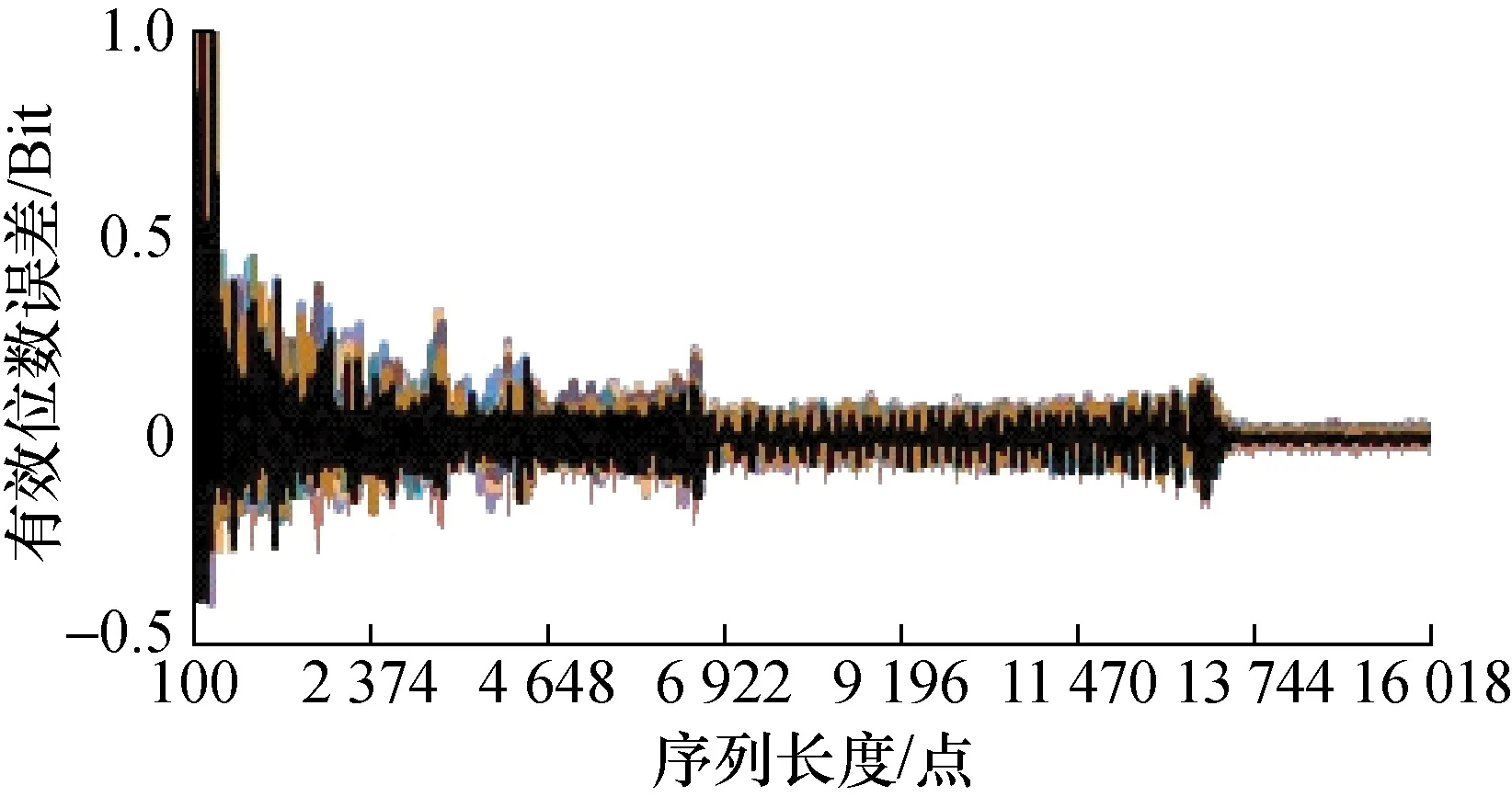
图20 数据点数与直流分量变化时有效位数误差

其中,图1、图10、图14、图18中的辅助变量周波数变化范围为1～20,步进值1；每图均为20条曲线共同结果。

图2、图6、图15、图19中的辅助变量初始相位变化范围为-180°～180°,10°步进；每图均为37条曲线共同结果。

图3、图7、图11、图20中的辅助变量直流分量变化范围为-0.5～0.5 LSB；0.05 LSB步进；每图均为21条曲线共同结果。

图4、图8、图12、图16中的辅助变量序列长度变化范围为1 000～16 000点；1 000点步进；每图均为16条曲线共同结果。

图5、图9、图13、图17中的辅助变量幅度为82.031 25%×半量程,其变化范围-0.5～0.5 LSB,0.05 LSB步进。每图均为21条曲线共同结果。

从图1～图4可见,信号幅度由小变大时,有效位数的误差界将由大变小,其变化最大时可以导致±0.1 Bit的有效位数误差,当信号幅度在半量程以上时,有效位数误差界可以在±0.03 Bit以内。

从图13～图16可见,直流分量变化时,有效位数的误差界将产生变化,其变化最大时可以导致±0.03 Bit的有效位数误差。

从图2,图9～图11,图14、图15可见,与幅度变化及直流分量变化带来的影响相比,初始相位变化对有效位数的影响处于次要地位,可以忽略。

从图5～图7,图10可见,周波数的变化对有效位数的误差界影响小于幅度变化和直流分量变化带来的影响,但也不可忽略,需要深入研究。

从图17～图20可见,序列长度较小时,将带来显著误差,而序列长度增加,将使得其对有效位数的误差贡献降低,但也不是单调降低,其变化规律需要进一步研究。

3.3 序列长度变化时仿真实验结果分析

在8 bit A/D情况下,按上述条件,用序列长度参量为主变化因素,分别以幅度、周波数、初始相位、直流分量为辅助变化因素生成的仿真数据,计算获得的动态有效位数估计误差随着各因素而变化的情况,如图17～图20中所示。

1)幅度作为辅助变量,获得如图17所述动态有效位数误差变化曲线波形。

2)周波数作为辅助变量,获得如图18所述动态有效位数误差变化曲线波形。

3)初始相位作为辅助变量,获得如图19所述动态有效位数误差变化曲线波形。

4)直流分量作为辅助变量,获得如图20所述动态有效位数误差变化曲线波形。

从图17～图20可见,当其它辅助条件完全相同时,随着序列长度由小到大,动态有效位数的误差界总体上呈下降趋势。但并非单调下降,而是呈现出某种具有量化台阶式的量化特征。

经过对上述图17～图20曲线波形的全面关联性规律分析,发现信号序列内包含的周波数与序列长度组合变化时,其动态有效位数误差量化台阶规律特征明显。

不失一般性,令序列所含信号周波数从1～20范围内变化,令序列长度从100～16 000之间变化,则获得仿真计算结果可见:

当周波数固定时,序列长度从小到大变化时,有效位数误差界呈等间隔阶梯式减小；如图21～图26所示。其中,图21为单周波序列,图22为双周波序列,图23为4周波序列,图24为8周波序列,图25为19周波序列,图26为20周波序列。

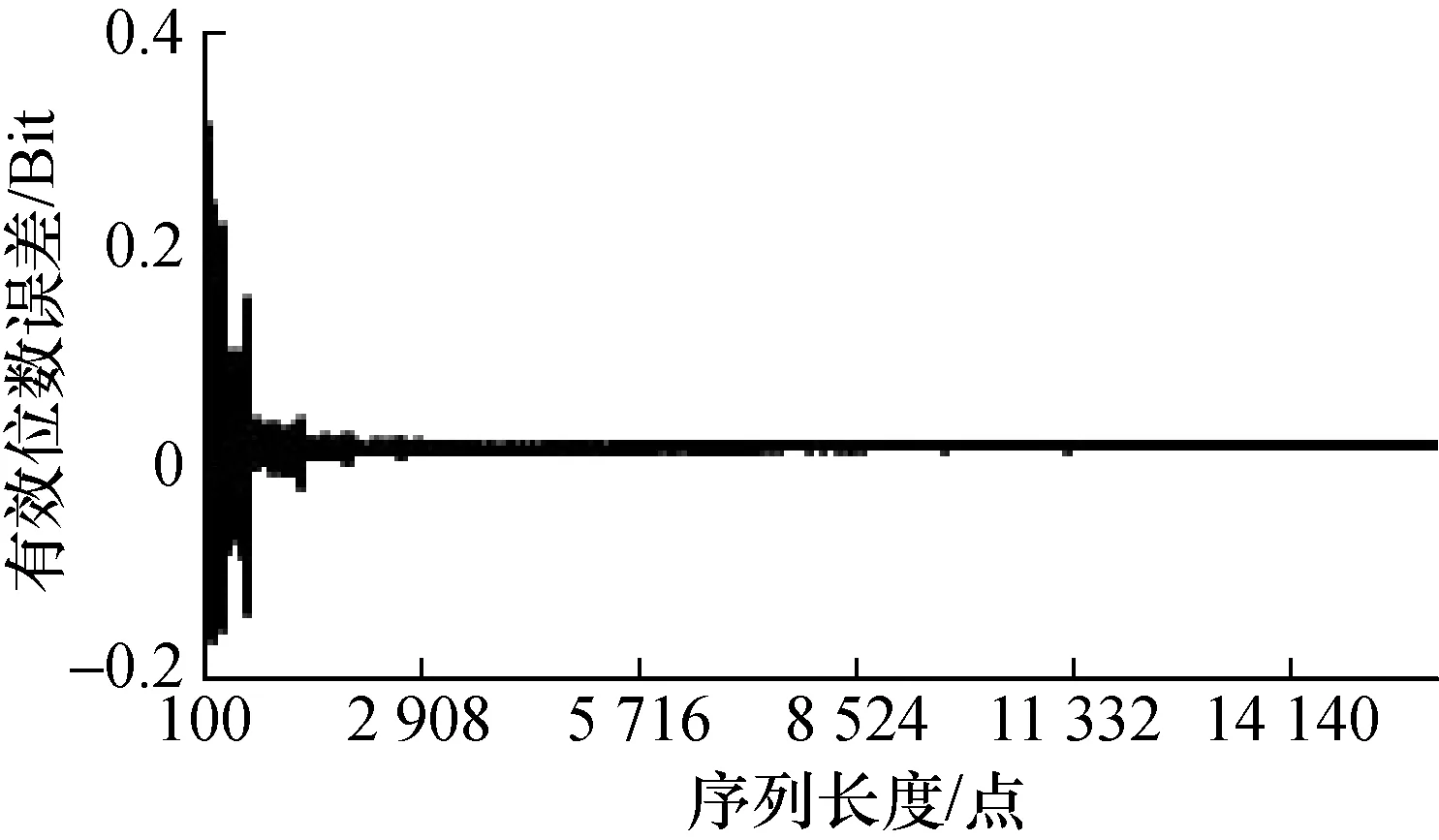
图21 有效位数误差随序列长度变化情况

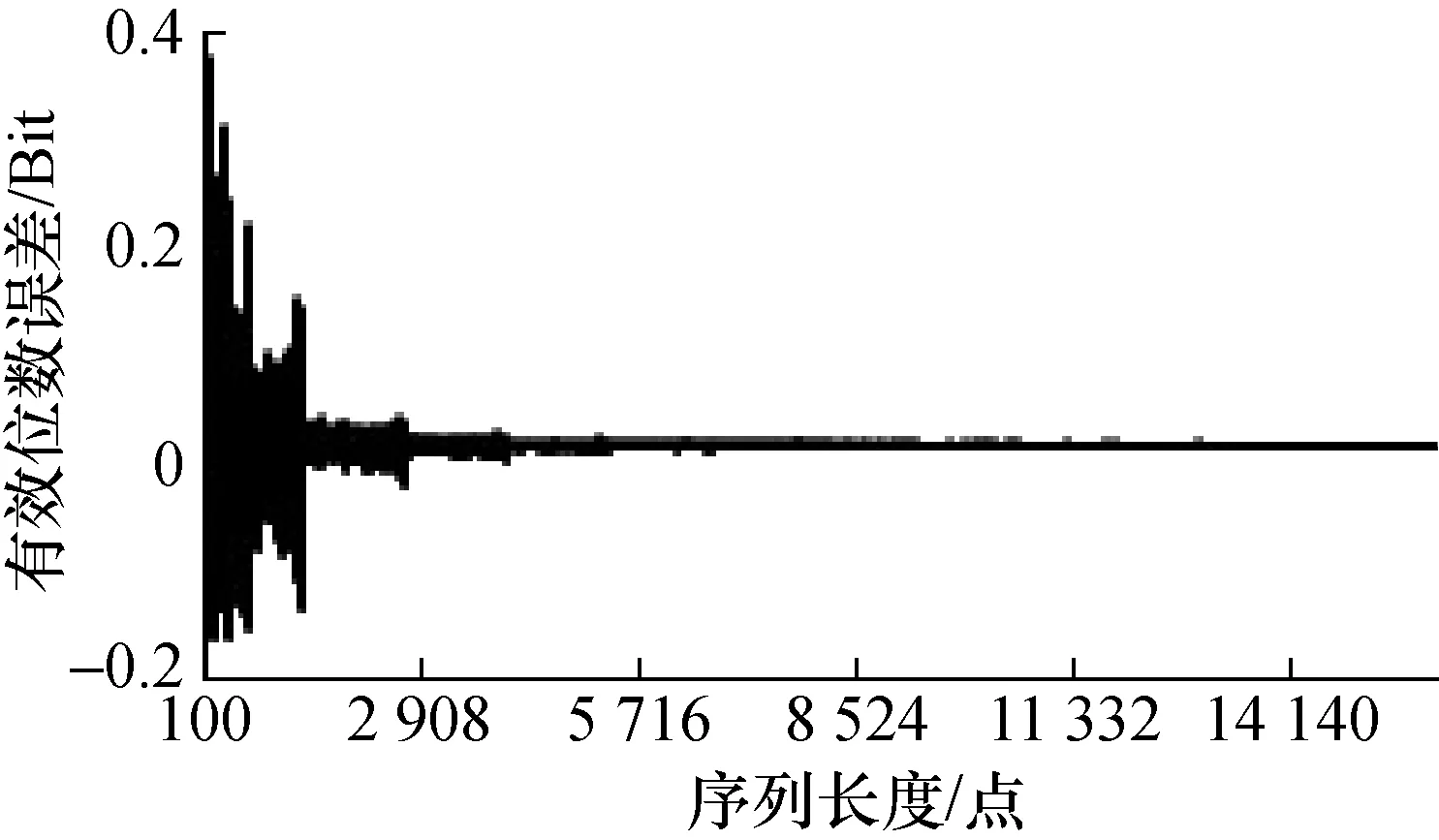
图22 有效位数误差随序列长度变化情况

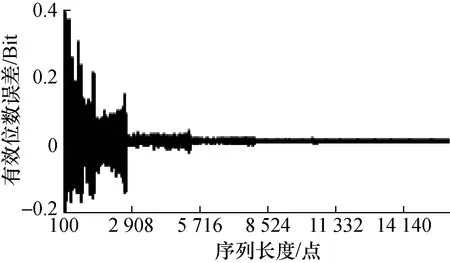
图23 有效位数误差随序列长度变化情况

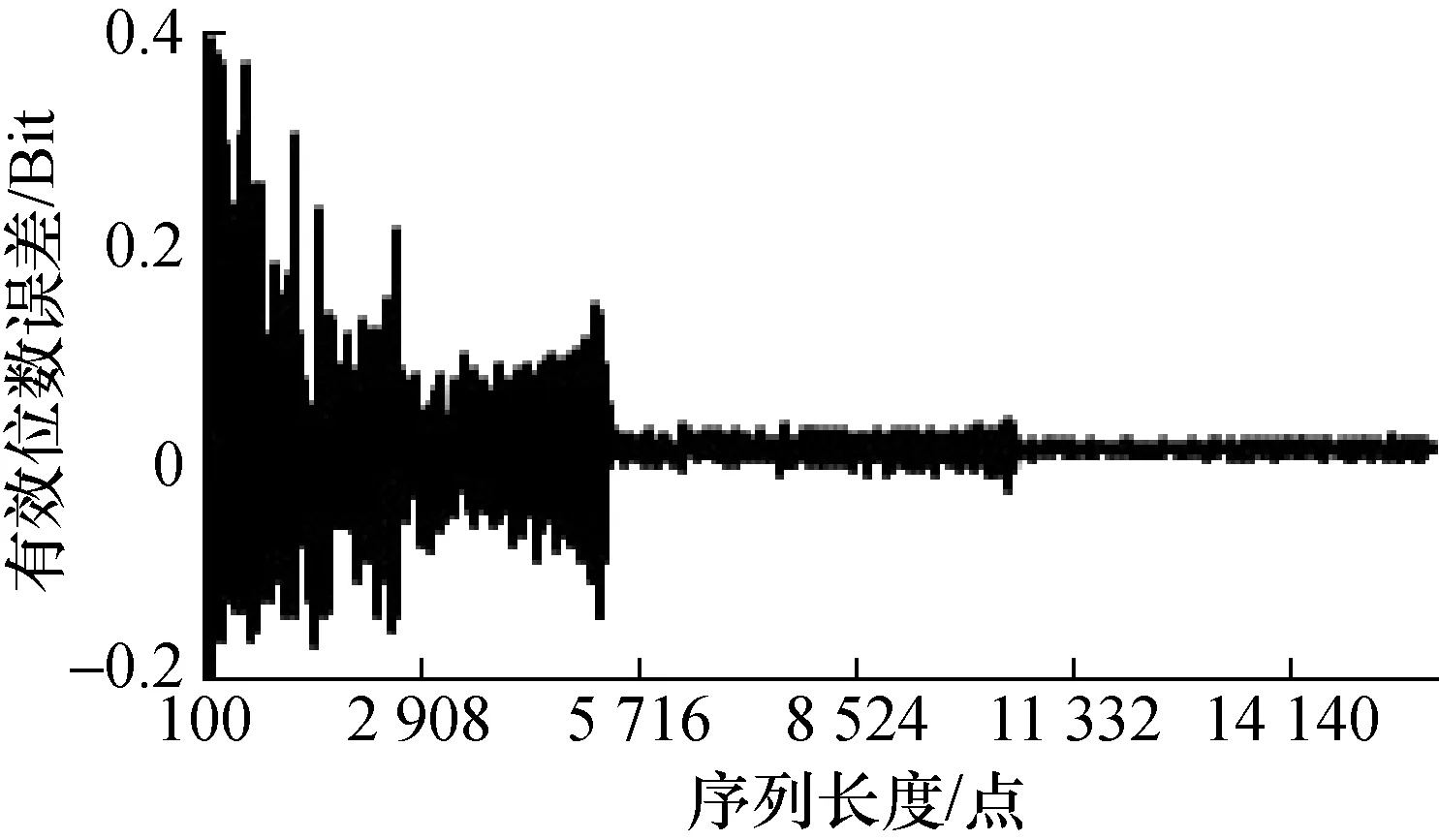
图24 有效位数误差随序列长度变化情况

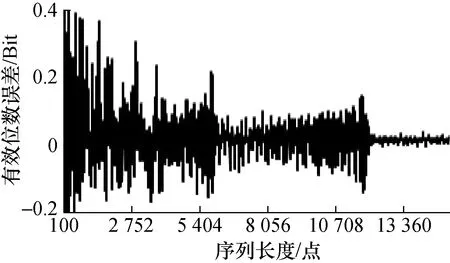
图25 有效位数误差随序列长度变化情况

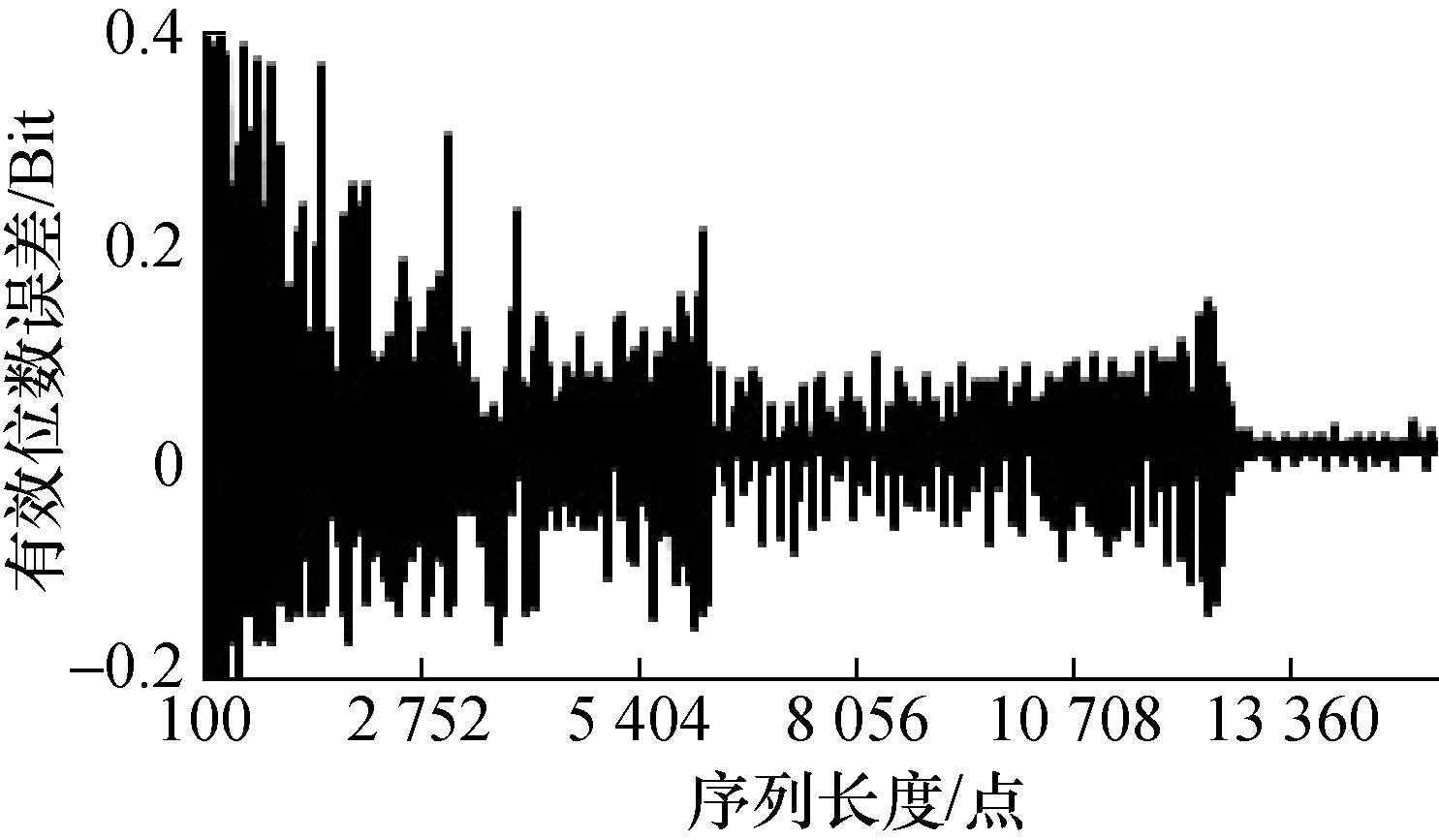
图26 有效位数误差随序列长度变化情况

仿真试验表明:

1)在A/D位数相同时,动态有效位数误差随着波形序列长度和序列所含周波数不同,呈有规律的量子化阶梯变化趋势。

2)周波数相同时,不同的量子化误差阶梯近似等长度,误差界的范围跳变很大,且随序列长度增加呈快速递减规律；而在同一个量子化误差阶梯上,误差界随序列长度增加呈平稳而缓慢增大趋势。

但第1个量子化误差阶梯除外,它的变化规律复杂,是一个中间低两头高的马鞍型误差阶梯。

3)不同周波数的量子化误差阶梯的长度与周波数成正比。

在实际测量时,应尽量使得测量条件落到高序号量子化误差阶梯之内,至少是第2个误差阶梯上。尽量避免测量条件落入第1个误差阶梯上。

称每一个量子化误差阶梯宽度为台阶宽度。

4)从仿真计算结果曲线及变化规律可见,宽台阶近似于窄台阶的线性拉伸。在拉伸延展过程中,同一台阶误差带基本保持稳定,可以近似看作仅仅是长度展宽。如图21～图26所示。

如图25和图26所示,两者均只有第一个完整台阶和第二个台阶的一部分。观察分析周波数相邻的几条误差曲线,如图21～图24很容易发现该规律。

以误差曲线台阶末端跳变峰值来寻找各级误差台阶末端点,并将其列表如表1所示。

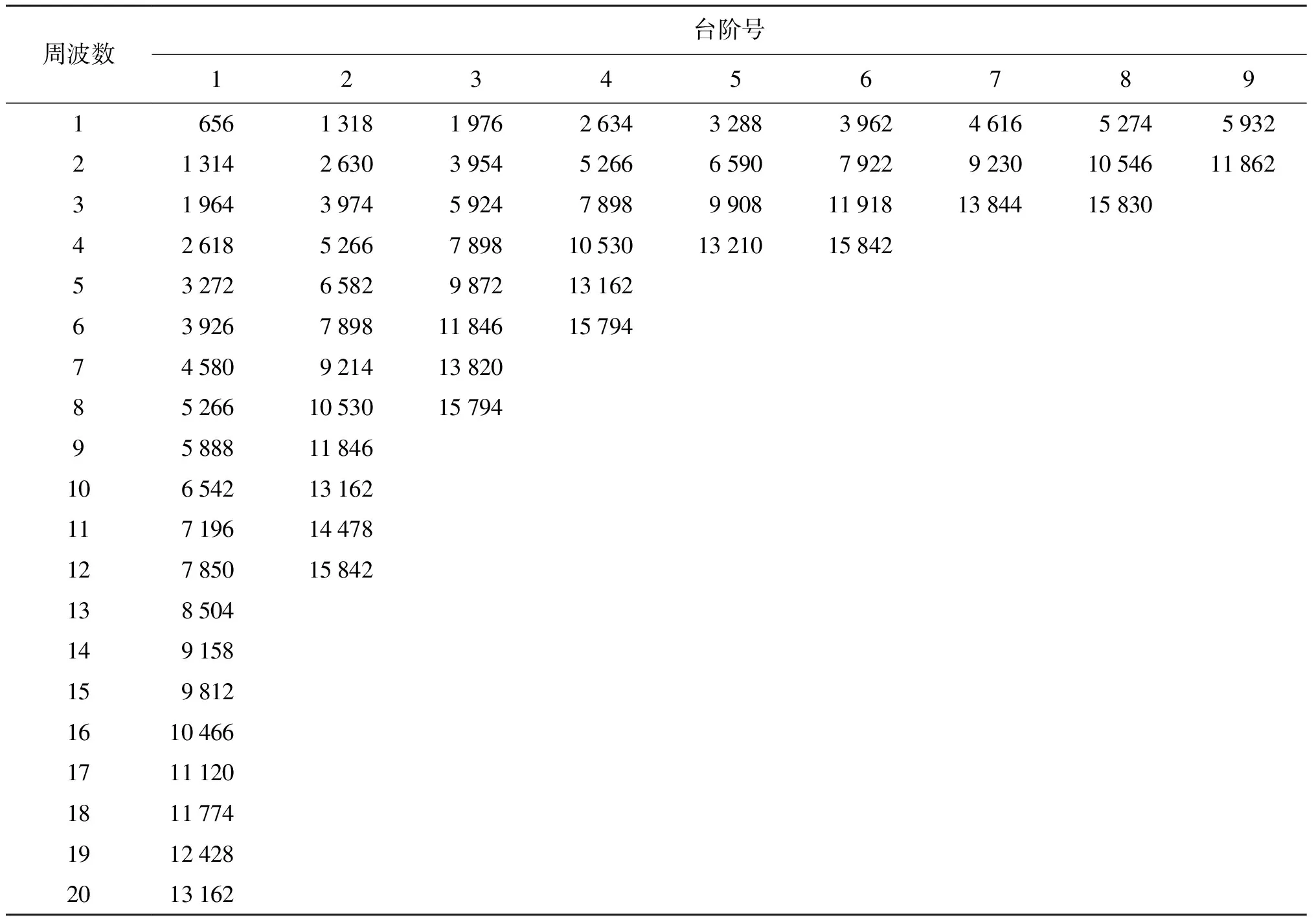
表1 有效位数误差台阶末端点实测表(8位A/D)

令含j个周波的序列的第i个误差台阶的末端点为ti,j,通过相同周波数据最小二乘线性拟合,得直线方程:

ti,j=G*,j×i+T*,j

(1)

通过相同台阶序号数据最小二乘线性拟合,得直线方程:

ti,j=Gi,*×j+Ti,*

(2)

对上述表1中的台阶末端点数据进行相同周波数据横向最小二乘拟合得结果如表2所示。

进行相同台阶序号数据纵向最小二乘拟合得结果如表3所示。

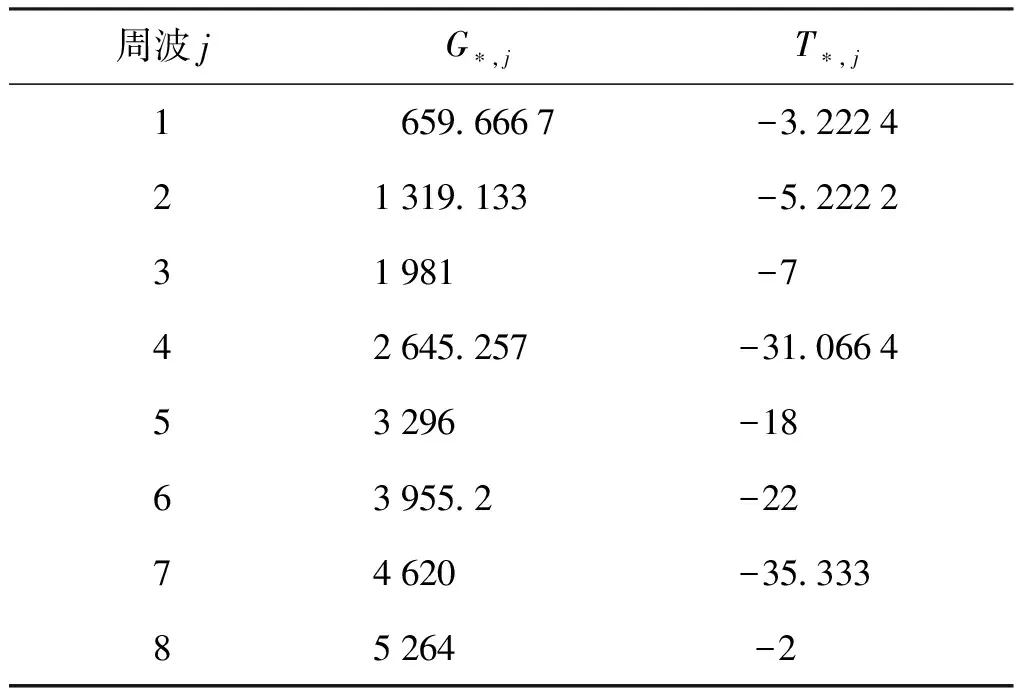
表2 j个周波不同台阶数据最小二乘拟合结果

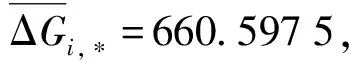
表3 i个台阶不同周波数据最小二乘拟合结果

综合各个方面的因素,可以获得对于8位A/D而言,Gi,*=660是一个核心结果,含j个周波的序列的台阶宽度约为660×j个采样点。

令量子化常数Gz=660,对于含j个周波的序列的第i个台阶末端点ti,j,有:

ti,j=Gz×j×i

(3)

3.4 A/D位数变化时仿真实验结果分析

其它仿真条件保持不变,分别调整变化A/D位数分别为7、9、10 bit,获得有效位数误差特性曲线,以误差曲线台阶末端跳变峰值来寻找各级误差台阶末端点,并将其列表如表4～表6所示。

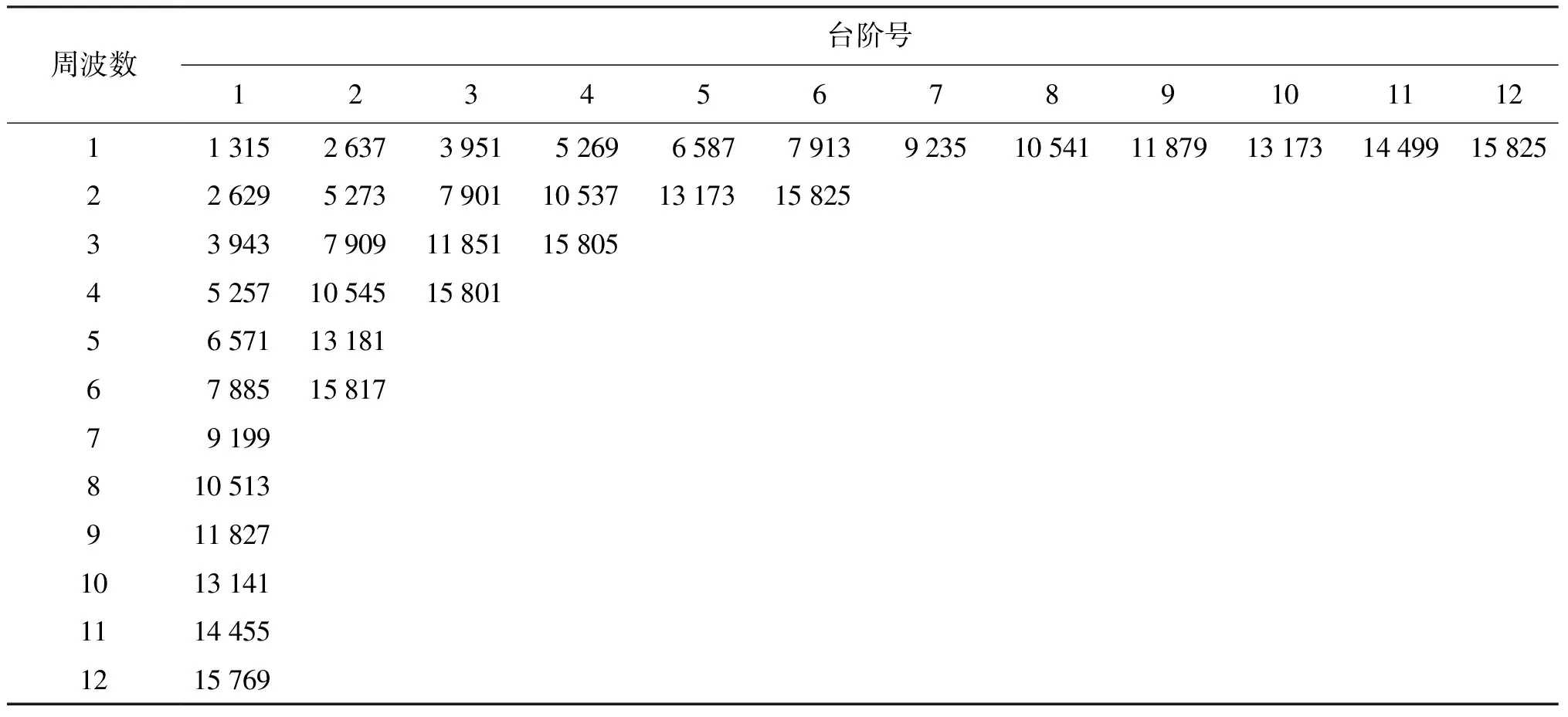
表4 有效位数误差台阶末端点实测表(9位A/D)

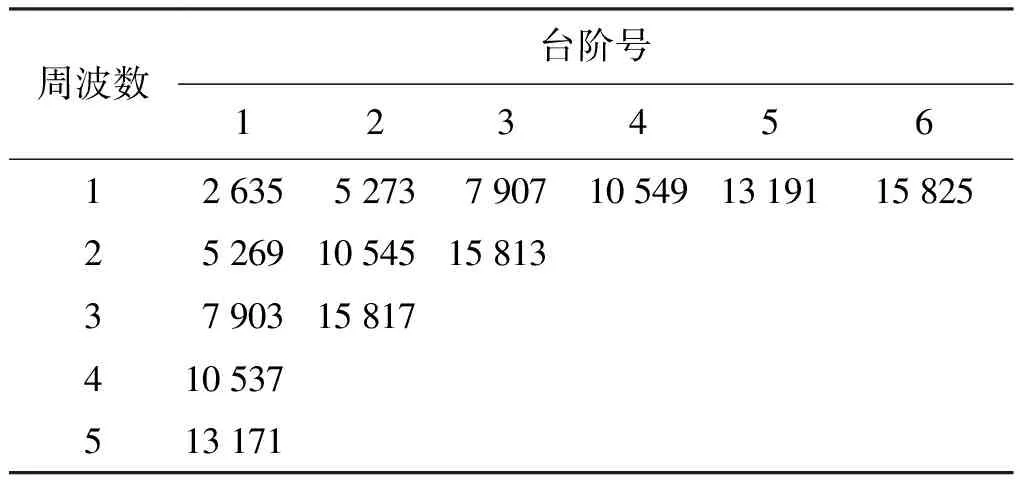
表5 有效位数误差台阶末端点实测表(10位A/D)

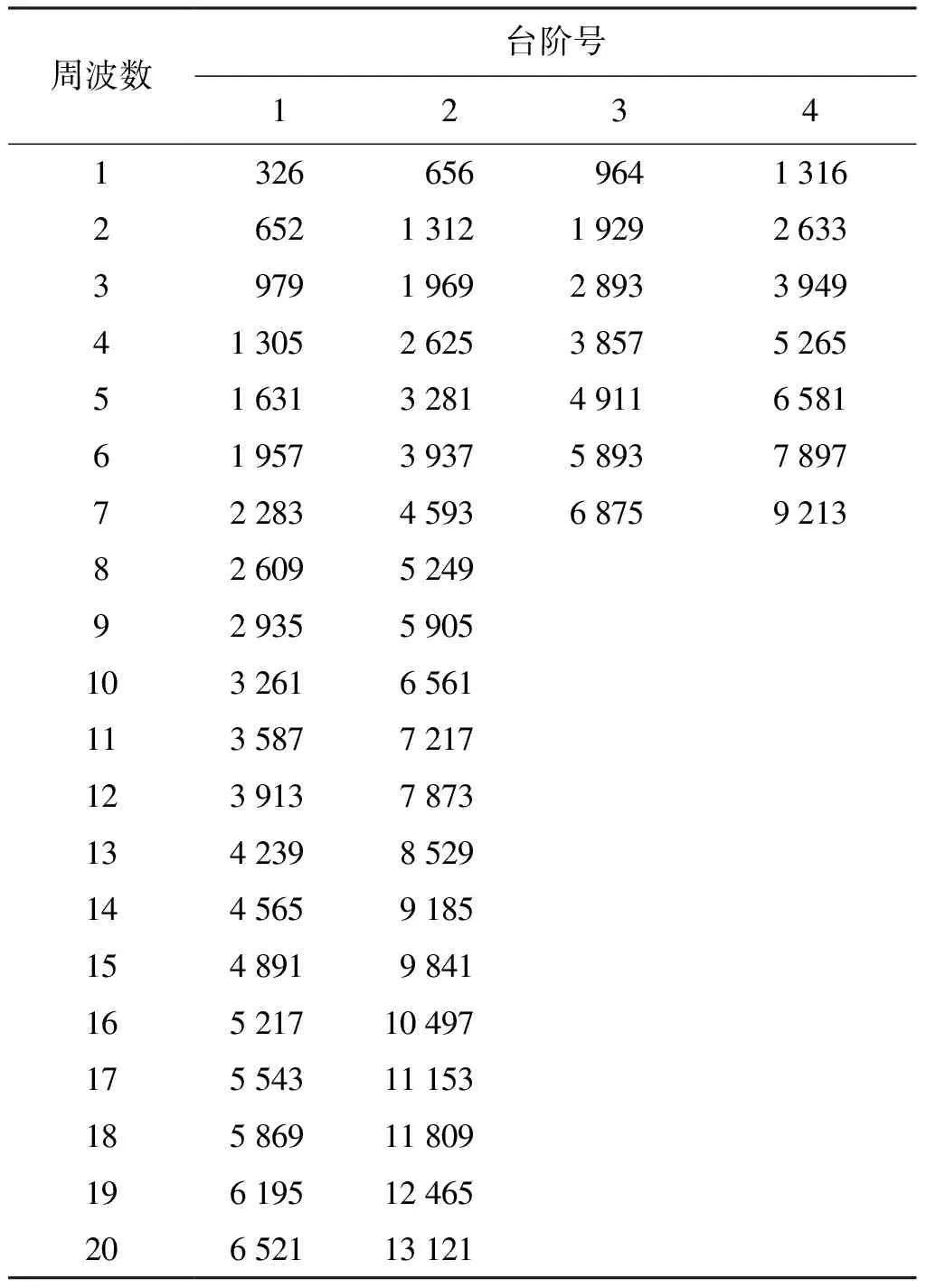
表6 有效位数误差台阶末端点实测表(7位A/D)

经过与上述8位A/D相同的处理过程,获得如表7所述计算结果。

由表7的仿真计算结果可见,相同周波条件下,动态有效位数误差随序列长度增加而呈等间隔阶梯分布,依次为第1阶梯、第2阶梯等。不同阶梯的误差界随阶梯数增高呈下降趋势,降到一定程度后误差界趋于平稳。

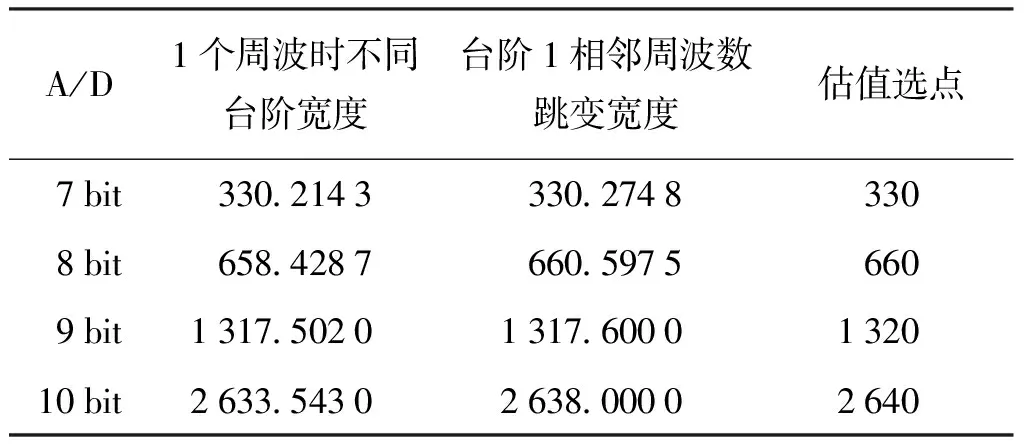
表7 有效位数误差阶梯参数(数据点数)

动态有效位数误差阶梯宽度与A/D位数、序列所包含的周波数等均有线性关系。

在相同A/D位数情况下,误差阶梯宽度与序列所包含的周波数呈线性关系；在不同A/D位数情况下,同一周波数的同一序号误差阶梯宽度与A/D位数成正比。

综合各个方面的因素,可以获得对于8位及以上位数的k位A/D而言,含j个周波的序列的台阶宽度为Gz×(k-7)×j个采样点。对于含j个周波的序列的第i个台阶末端点ti,j,k,有:

ti,j,k=Gz×(k-7)×j×i

(4)

对于8位以下位数的k位A/D而言,含j个周波的序列的台阶宽度为Gz÷(9-k)×j个采样点。对于含j个周波的序列的第i个台阶末端点ti,j,k,有:

ti,j,k=Gz÷(9-k)×j×i

(5)

式(4)、式(5)可用于估计各个测量条件下动态有效位数误差阶梯末端点位置,以便进行动态有效位数评定误差和不确定度的控制。

4 讨论

本文选取了6个条件作为仿真研究要素,对动态有效位数估计误差随各个条件的变化情况进行了仿真研究。实验表明,动态有效位数的估计误差随序列样本长度的变化呈阶梯状量化跳变规律变化。并对阶梯宽度随样本长度、样本内所含周波数、A/D位数等要素的变化进行了定量分析,获得了动态有效位数估计误差界随各个因素而变化的经验公式。可用于估计任意一款A/D采样序列的有效位数评价时的误差阶梯边界点。进而用于指导测量条件的选择和确定。

仿真结果表明,相同A/D位数条件下,含有不同周波数的有效位数测量结果,其相同序号的误差阶梯的末边界点的误差界波动较小,可认为近似相同。并且,随着A/D位数的增高而呈缓慢下降趋势。这也充分体现了误差界阶梯序号的实际意义和价值。通常,应该尽量避免使用第1个误差阶梯的测量条件。

另外,由于误差阶梯边界是使用误差峰值点识别获得的,因而,实际上若以误差界水平定义的本误差阶梯的宽度要略宽于该峰值边界点才更为合理可行。即,使用误差阶梯条件时,应尽量避免在误差阶梯边界点附近使用,应该比边界点多10%～20%的误差阶梯宽度以上使用,才可确保误差界落到下一个误差阶梯内。实际应用中应予以注意。

最后,需要特别说明的是,该结论和规律是在仅存在量化误差的仿真条件下获得的结论。没有任何随机误差因素参与其中。实际工作中,很难出现这样理想的测量状况,总会有随机因素误差出现在实际信号中,特别是小信号和微弱信号的采集测量中,随机误差可能占据主导地位。那时,本文上述结论将不再适用,但未知噪声影响是否占据主导地位的情况下,均可参照上述规律设定测量条件,将没有任何害处。