基于光子能量测定的普朗克常数直接测量法

李玉芬, 和穗荣, 韦联福

(西南交通大学 信息科学与技术学院,四川 成都 610031)

1 引 言

普朗克常数是物理学中的基本物理常数之一。各种量子效应观测、普朗克长度和普朗克时间尺度的确定,均与普朗克常数的精确测定密不可分。2019年5月20日,国际度量衡委员会(CIPM)批准推荐国际科技数据委员会(CODATA)将该常数的平差结果h=6.626 070 150(69)×10-34J·s[1](其相对不确定度为1.0×10-8)定义为普朗克常数的精确值,用来重新定义SI基本单位千克,代替千克实物基准——国际千克原器(IPK)[2,3]。

早期普朗克常数的测量方法都是间接的,即通过测量普朗克常数与另一个常数的比值,如h/e、h/e2、h/c等来间接得到普朗克常数值。由于这类测量中包含其它具有一定相对不确定度的物理量,如基本电荷单位e和真空中的光速c等,所以这些间接测量是以比值形式的结果作为实验结果,并不能直接得到普朗克常数的值和不确定度[4]。

近年来,力学平衡法,包含多种电流天平[5]和电压天平[6,7]方法、基布尔秤[8,9](功率天平)以及我国提出的能量天平[10～13]被广泛应用于普朗克常数的精密测量。其中,利用超导磁悬浮[14]、功率天平和能量天平可以实现普朗克常数的直接测量[15],其中最好结果是加拿大国家研究委员会(NRC)使用功率天平测得的相对不确定度为9.1×10-9的值h=6.626 070 133(60)×10-34J·s[16]。显然,直接测量方法在测量精度上比早年间接测量方法有明显的优势。但是,基于功率天平和能量天平方法的直接测量法所得到的精度仍受限于诸多物理参量,如线圈磁场、线圈长度、切割磁感线的瞬时速度、感应电压和互感值等的测量精度,所以仍有很大的提升空间。尤其是,相比于现有的时间(频率)测量精度,现有的普朗克常数测量精度仍然可继续提高。

本文从分析传统光电效应实现普朗克常数间接测量的方法出发,利用入射光功率与输出电功率的等价关系,提出了一种可以在不引入其他基本物理参数测量的情况下,实现普朗克常数值精密测量的方法。

2 光电效应法间接测量普朗克常数

跟据光子的能量公式:

E=nhf

(1)

式中:E为光子能量；n为光子数；h为普朗克常数；f为光的频率。

利用入射光功率与输出电功率的等价关系,提出一种可以在不引入其他基本物理参数测量的情况下,实现普朗克常数值精密测量的方法。式(1)中,E由光电效应实验中的饱和电流台阶给出,n由光子数可分辨的光子探测器进行精确测量。由于目前测量频率的精度很高,而且本方法所需测量的参量仅有2个,尤其是利用液氦上的表面电子态电离技术避开光电效应中逸出功的测量,从而可以在极低温的环境下(热噪声可忽略不计)实现精密测量。

光电效应实验原理如图1所示。用光照射阴极板K,使阴极金属板的电子逸出,给两极板外加电压,在电场力的作用下光电子以更快的速度打到阳极板A上,此时电子的定向移动产生一个相对较容易测量的电流。

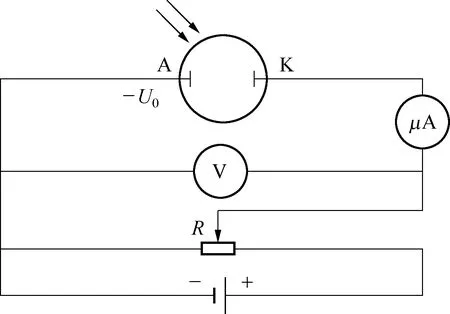
图1 光电效应实验原理图

光电效应由爱因斯坦方程描述:

(2)

式中:hf表示频率为f的光子具有的能量；m和v0分别是光电子的质量和最大速度；W为电子摆脱金属表面约束所需要的逸出功,由金属材料决定。假设所有电子逸出速度均为沿垂直阳极板面方向的理想状态,电子逸出速度均是最大速度。因此,光子能量一部分用于克服束缚成功逸出,一部分转化成逸出后的动能。显然,产生光电效应现象的基本要求是,入射光能量hf至少要能够让电子克服逸出功W,所对应的频率f0称为光电效应的截止频率:

(3)

不同金属有不同的逸出功,所以截止频率也是不同的,本文默认实验所选取的入射光频率f>f0。

当阳极A的电势为正,阴极K电势为负时,阴极板被打出的光电子受到阳极板正电荷的吸引,光电子被加速。但是,当阳极A电势为负,阴极K电势为正时,光电子被减速；如果A、K之间电势差足够大,具有最大逸出动能的光电子也被反向电场所阻挡,无法运动到阳极板,光电流将为0,此时

(4)

式中:e为电子电量；U0是截止电压。当反向电压达到截止电压U0时,光电流为0。结合以上3个方程可以得到关系:

eU0=hf-W=hf-hf0

(5)

即

(6)

可见,截止电压U0是入射光频率f的线性函数,其斜率等于h/e。实验中,用不同频率的光照射,测得不同的截止电压；照射到不同逸出功材料上,可测得一系列的截止电压-频率直线,但这些直线的斜率都是h/e,如图2所示。

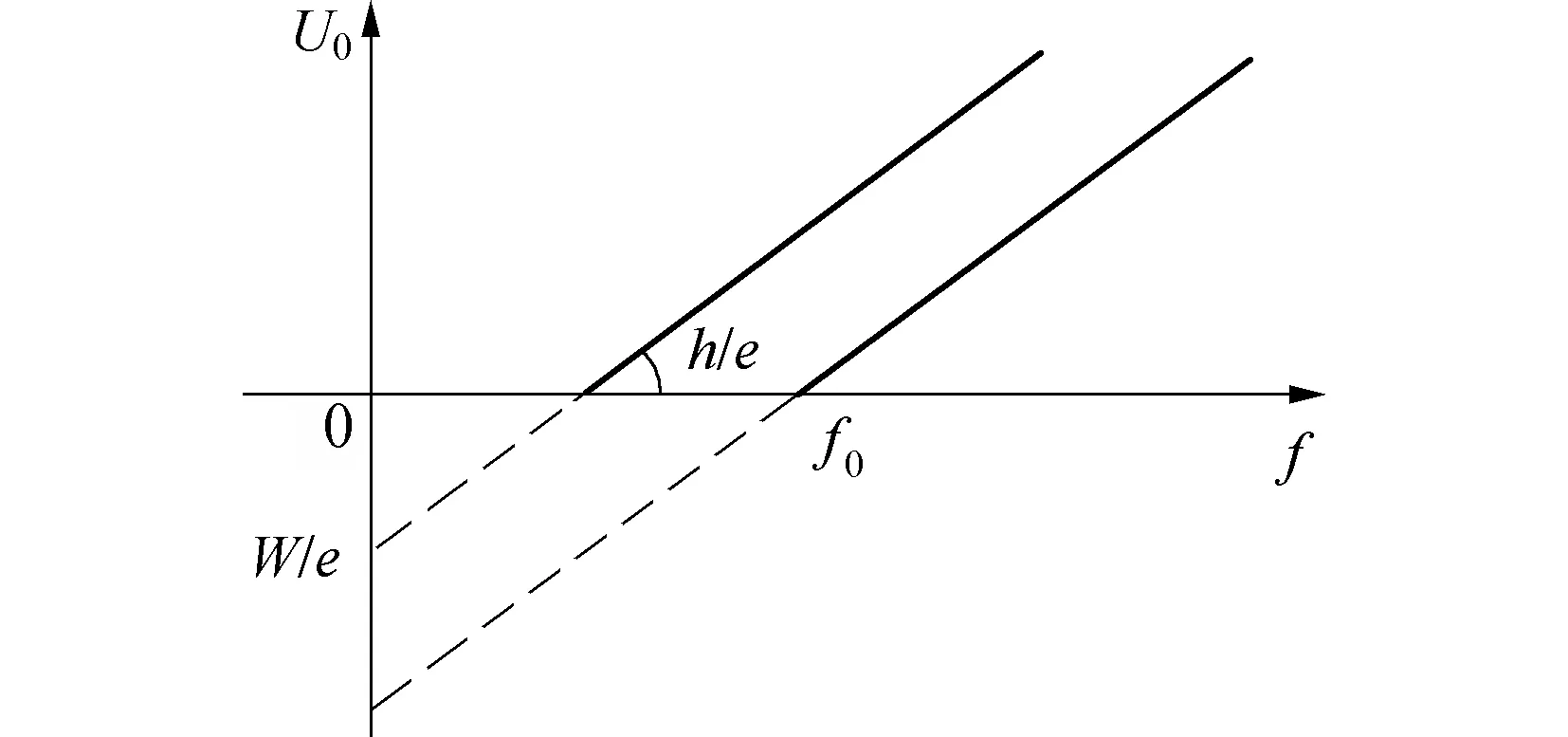
图2 常用的光电效应斜率法测普朗克常数

所以,由实验测量数据所得到的直线斜率即可求得h/e的大小,再利用基本电荷单位e的值就可以间接地测得普朗克常数值,这就是通常由光电效应测量普朗克常数的基本原理。当然,这里所实现的普朗克常数测量还是受限于电子电荷e的精度,按CODATA 2017的国际推荐数值,其精度水平为5.2×10-9[1],所以通过测量h/e来计算普朗克常数的精度水平很难超过目前CODATA推荐的不确定度1.0×10-8,难以达到10-9甚至更高精度水平。此为传统光电效应实验间接测量普朗克常数难以进一步提高测量精度的物理限制。

根据热电子发射的理查森定律,通过室温下的光电效应来间接测量普朗克常数,会受到极大热噪声导致暗电流,从而对截止电压的测量精度造成很大的影响。因此,在极低温环境下进行光电效应测量非常必要。可以预计,在接近绝对零度的极低温情况下,热激发所造成的误差水平将大大下降,从而能极大程度地减小暗电流对截止电压测定的影响,实验将得到更准确的结果。但是,即使这样,光电效应实验间接测量普朗克常数的精度仍无法绕过电子电荷e的有限精度影响,难以进一步提高普朗克常数的测量精度；此外,光电效应实验中阴极材料的逸出功本身就难以精确测定。所以,进一步提高测量精度的最终解决方案,应该是通过光子能量法来实现直接测定普朗克常数。

3 光子能量法直接测量普朗克常数

3.1 基本原理

通过h/e的测定来间接得到h值的方法,精度自然受电子电量e本身测量精度的影响。所以规避e从而进一步提高普朗克常数测量精度是一个值得探索的方向。实际上,跟据光束能量式(1)可知,如果可以测量一束光单位时间内入射光子数n(由光子计数技术进行精密测量),那么再测量光功率E,就可以实现普朗克常数的直接测量。显然,这一直接方法的精度,不再受限于另一个常数测量的精度；且光频率f的测量精度目前已达到10-18的水平,因此直接测量普朗克常数其精度有望得到更大的提升。

物理上,利用光电效应也可以实现规避e测量精度的影响,实现普朗克常数的直接测量。当然,与传统光电效应实验通过测量截止电压来间接实现普朗克常数测量方法有本质上的不同,在这一实验中,需要精确测量的量不再是截止电压而是饱和光电流。其基本原理是,因为单位时间一束入射光的能量(即光功率)E与光子数n有式(1)所示关系,因此光能量E可以通过测量饱和光电流来确定

E=UImaxImax

(7)

式中:Imax为饱和光电流；UImax为电流达到饱和值临界处时的电压。联立式(1)和式(7)可以将普朗克常数直接计算出来,从而规避了e的精确度的影响。这里,测量精度取决于饱和电压UImax的测量精度。由于基于量子霍尔效应测量电阻的测量精度[17]已经能达到10-10,而且基于约瑟夫森效应已经建立了电压测量的量子物理基准[18],所以饱和电流的测量精度至少可以达到电阻测量精度水平。

此外,光子能量法直接测量普朗克常数中,光束光子数的测量也同样重要。幸运的是,近年发展起来的可分辨光子数光子探测技术,实现了弱光光子数的直接计数。如美国NIST在单个工作于100 mK的低温超导转移边缘传感器(TES)芯片上实现了 1 000个光子的准确识别[19]；利用不同光子数下超导谐振器动态电感的不同响应,本实验室实现了直到7个光子的可分辨探测[20]；由于光电效应的发生只取决于入射光的频率,而入射光的强度仅决定了出射光电子数的多少(可通过光电效应的饱和电流大小来测定),所以利用极低温条件下的光电效应饱和光电流对应电压台阶的测量,来实现普朗克常数的直接测量是切实可行的。

3.2 饱和电流的测定

固定入射光线频率和强度,逐渐加大正向偏置电压到一个足够大的值后,电流将不再随着电压的增加而增大,形成饱和光电流。这是通常光电效应实验所观测到的现象。这是因为,在电场力的作用下,所有逸出的电子都可以在单位时间内由阴极金属板打到阳极板上；继续加大电压只会缩短电子在两极板之间的运动时间,相当于减少了电子在极板间运动时的体密度,从而使得电流不再变化。

利用能量守恒关系,可得到电子在光电管中某处x=xt的体密度[21]为:

(8)

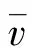
(9)

可见,饱和光电流Imax只与单位时间内阴极发出的电子数有关,与所加偏置电压无关。物理上,决定单位时间内阴极板逸出光电子数量的是入射光单位时间内入射光子数:1个电子最多只能吸收1个光子的能量,即1个光子最多使1个电子逸出,所以单位时间内逸出光电子数小于或等于入射光子数。当然,相同强度的光的能量是相同的,能量E与光子数n和光频率f由式(1)相联系。所以,固定入射光频率后,光照强度越强光子数目越多,从而单位时间能打出的电子数越多、饱和电流越大。

固定入射光光强和频率进行光电效应实验,通过改变电压可得到I-U曲线,如图3所示。这是通常光电效应实验都能观测到的现象。

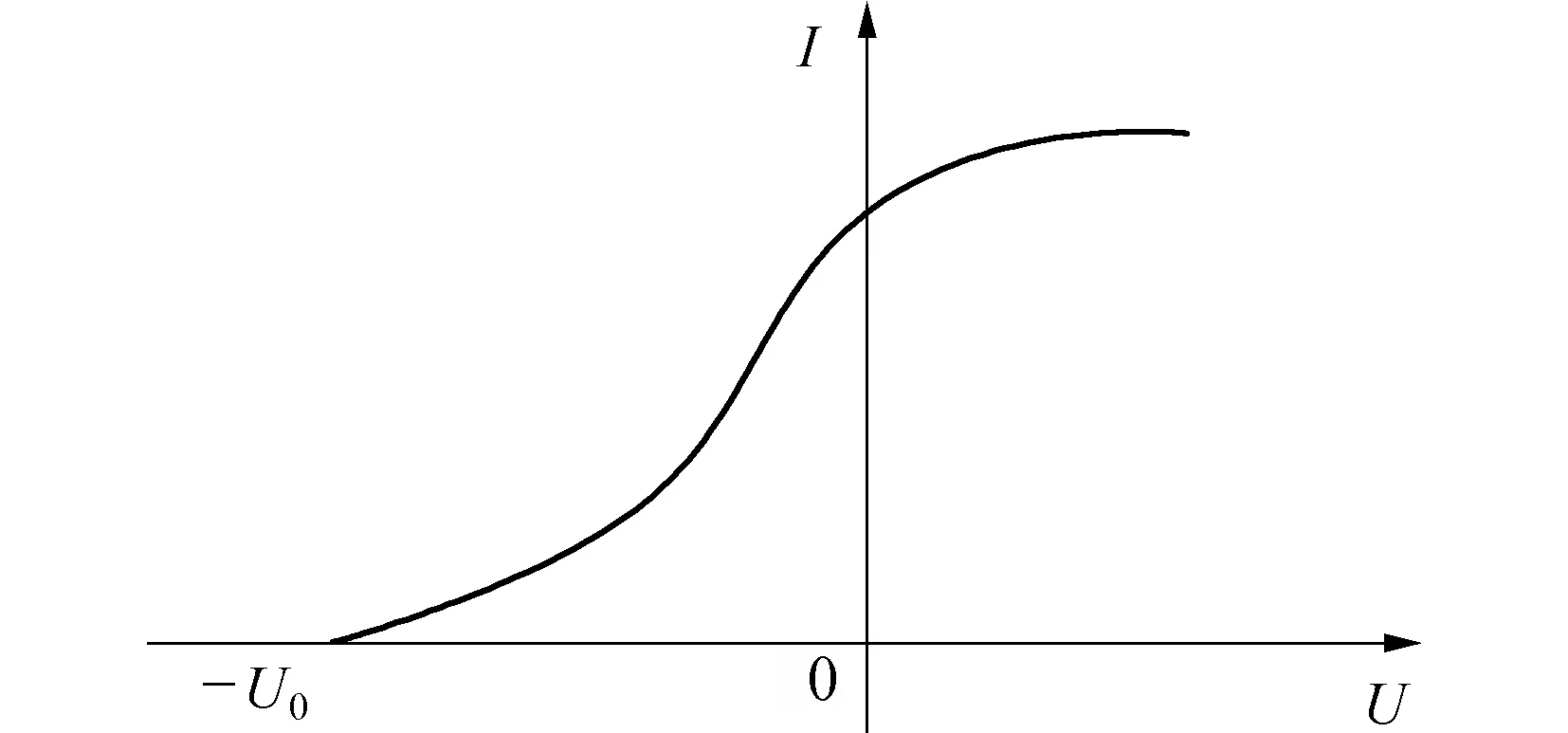
图3 光电流的伏安特性曲线

首先,阴极中的自由电子遵循费米-狄拉克统计:

(10)

式中:f(E)是电子具有能量E的概率；EF是费米能级；T是绝对温度；kB是玻尔兹曼常数。

因此,光电流I与阴、阳极之间电压U变化的关系可表示为[22]:

(11)

式中:δ是阴、阳极表面差异引起的电势差；ε是光电子的动能；εm=hf-W是光电子在0 K时从金属表面发射出来的最大动能。利用式(7)即可得到入射光光功率。

最后,再由式(1)即可得到普朗克常数的值:

(12)

这样,通过测定入射光脉冲的光子数n,就建立了普朗克常数与光频率的直接联系,由此可实现普朗克常数的直接测量。

当然,这一方法实现普朗克常数的直接测量,需要使用严格的单光子源[23],即保障1个脉冲只有1个光子,那么n=1。但现实的问题是,目前严格的单光子源技术尚未完全成熟,所以实验上大多采用弱光脉冲来代替。这种弱光脉冲实际上是通过相干光的线性衰减而得到的,所以光脉冲中的光子数存在由泊松分布描述的涨落,由此导致影响饱和电流测定精度的光电子数目的涨落。改进的办法是测定饱和光电流台阶的平整度。

图4给出了弱光脉冲的光子数分布服从泊松分布情况下,不同平均光子数与对应饱和光电流台阶的初步模拟结果。

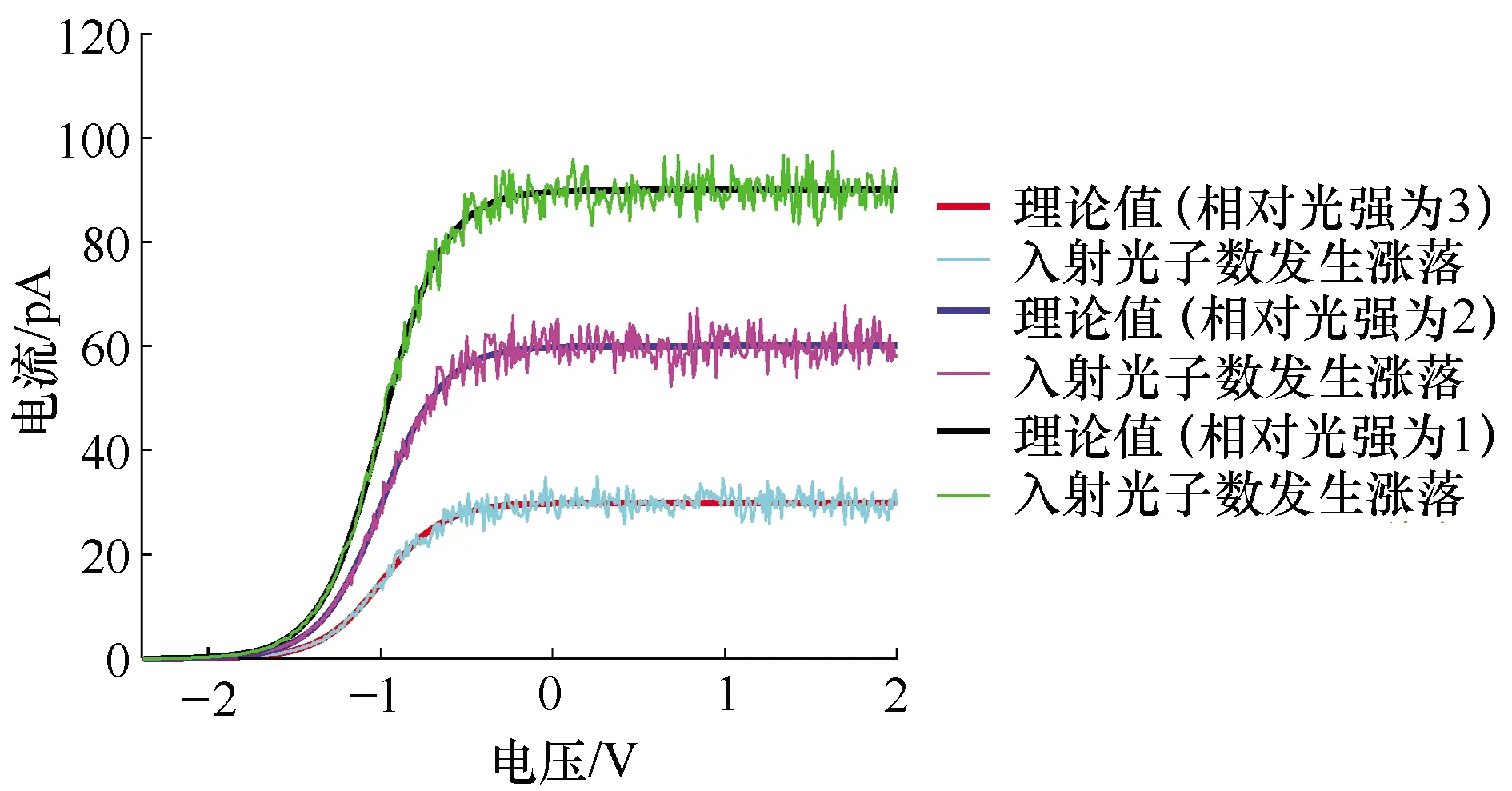
图4 不同平均光子数脉冲下饱和光电流的模拟

(13)

可见,当入射光频率一定时,不同光照强度(平均光子数不同)对应于不同台阶的饱和光电流,平均光子数越大则饱和电流越大。

另一个影响饱和光电流台阶平整度的主要因素是暗电流涨落幅度。减少暗电流的一个有效途径是降低光电效应实验中的环境温度。由阴极自由电子的费米-狄拉克分布式(10)可以看到,在稀释制冷机所提供的mK级环境温度中,暗电流涨落的影响将显著降低,从而可以大幅降低暗电流对饱和电流台阶平整度的影响。

3.3 实验系统设计

基于上述原理分析,设计了图5所示的极低温光电效应实验系统,其核心思想是尽可能地测得平整度好的饱和光电流台阶。实验系统的主要构成有:

图5 液氦上电子的光电效应系统原理图

(1)将充满氦气的密闭容器,置于稀释制冷机所提供的极低温环境中。在这一极低温(远低于氦气的液化温度)环境下容器中的氦气液化成液氦(蓝色部分)。

(2)由光纤1中引入的光脉冲入射到光阴极,克服阴极极板逸出功的电子逸出阴极,形成漂浮于液氦表面的光电子,它在垂直液面方向上形成类氢原子(受液氦表面的静电镜像势束缚)；电流表A1测量电流以确定液氦表面上光电子的存在。

(3)由光纤2引入弱光脉冲(单光子脉冲)照射液氦表面上的电子使其电离发生光电效应。电流表A2测量类氢原子电离所形成的光电流。

系统的基本工作原理为:

(1)悬浮与液氦表面的光电子,在液氦镜像势的作用下,在垂直液氦表面方向上受到束缚,形成类氢原子。

由于泡利不相容原理,光电子与液氦表面有一个约1 eV的势垒[24],确保电子不会进入液氦中。液氦表面环境特别洁净,漂浮于上的电子态的退相干来源几乎只有液氦表面的不平整性,因此液氦上电子的退相干时间可以达到秒量级[25],为电子态调控提供了更多便利。在没有外电场且忽略电子间相互作用(Vee(x,y,z))的情况下,液氦表面上电子在平行于液氦表面的方向z上自由运动,势能V∥(x,y)为0,在垂直液氦表面方向上具有类氢原子势V⊥[26]:

(14)

式中:Λ=(ε-1)/(4(ε+1))是有效介电常数；ε=1.057 23是液氦相对介电常数；ε0=8.854 187 812 8×10-12F/m是真空介电常数。

描述这一悬浮于液氦表面上的电子系统的哈密顿量是:

V⊥+V∥(x,y)+Vee(x,y,z)

(15)

其能级和相应能量本征函数可解析出,分别为:

(16)

和

(17)

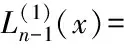
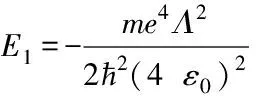
≈-0.658 1meV≈-159.12GHz

≈-0.164 5meV≈-39.78GHz

≈-0.073 1meV≈-17.68GHz

液氦上电子基态、第一激发态和第二激发态能量3个最低能级分布见图6。

图6 液氦上3个最低能级分布图

(2)类氢原子光致电离光电效应

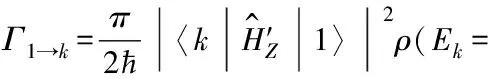
(18)

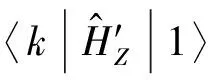
对于此系统,使用可见光f2照射液氦表面电子,使其发生光致电离时,电子由基态跃迁到平面波态所需能量远小于光子能量,则电子逸出时会有较大的初动能,光电流更易达到饱和,截止电压更大。此外,当外加电场为10 000 V/m时,用450～1 550 nm波长光使液氦上电子发生光致电离,光电离率Γ1→0与入射光角频率ω的关系如图7所示,选用频率较小的入射光将有更大的电离率。

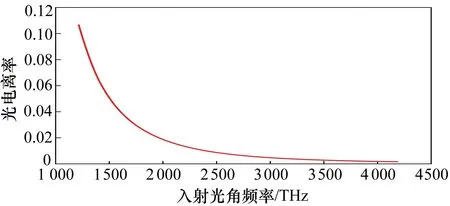
图7 光电离率Γ1→0与入射光角频率ω的关系

与传统光电效应间接测量普朗克常数的方法相比,本设计系统的潜在优势是:1)极低温环境大大降低热涨落导致的暗电流涨落；2)光电子逸出功,即类氢原子的电离能可以精确计算和测定；3)普朗克常数是通过与光子数有关的饱和光电流台阶的平整度来测量的。显然,除入射光的频率外,不再涉及其他参数的精确定义和测量,所以基于此极低温光电效应实验系统所实现的普朗克常数直接测量,精度有望得到较大的提升。

3.4 实现过程

第一步是确定液氦上电子的产生。通过光纤1使频率为f1的光子进入样品盒,并射击到阴极金属板上,调整不同光强或外加电压,通过电流表A1观察阴阳极金属板间光电流大小的变化。光电流应随着电压的增大而逐渐增大,并在一定程度上趋于饱和；保持外加电压稳定不变,成倍增大光强,光电流也有同样倍数的增大。满足以上情形,可以排除只有暗速率和场发射没有光电流的情况,还可根据需求调整电子数。

第二步是确定液氦上电子发生光致电离。通过光纤2入射能量为hf2的单光子脉冲,液氦上电子的电离能较小,所以可选用较小频率的光,当光子能量低于金属阴极的逸出功时,还可以避免金属阴极发生光电效应对实验结果的影响。改变光强或上下极板间的电压,通过电流表A2观察光电流的变化,判断方法与第一步相同。

第三步是进行对照实验排除噪声影响。极低温环境下实验热噪声较小,但仍不为零；随着电压的增强,场发射强度变大。这些都会使直接测出的饱和光电流平台不够平坦,所以需要减去无光情况下不同电压对应的电流大小。

第四步是重复同频率不同强度入射光的光致电离实验对UImax求平均值。改变光强即单位时间内光纤2的发射光子数,保持f2不变,实际饱和光电流将与光强发生同样倍数的变化,但临界饱和处的电压不变。所以,测量多组不同光强的光致电离,对UImax求平均值,将会得到更加准确的结果。

对于建立的输入光功率与输出电功率之间的等式关系:nhf=ImaxUImax,入射光频率f可以精确标定,而光子数n则由光子数可分辨技术精确分辨。对直接测量结果减去噪声测量结果得到的数据进行拟合等处理,得到平稳的饱和电流Imax台阶,首先达到饱和点的电压为UImax,这样就实现了普朗克常数的测量。

4 结 论

作为进一步提高普朗克常数测量精度的一种尝试,本文提出基于光子数分辨探测技术的光子能量法实现普朗克常数的直接测量。与间接测量不同,这里利用极低温光电效应和光子计数技术,建立nhf=ImaxUImax等式关系,因而可以实现普朗克常数直接测量。当然,本方法的实验实现也存在难点,如有效地实现液氦表面电子态、电子基态能谱测量及弱光照射下的微弱电离电流精确测量等等。