基于耗散结构理论的煤矿安全风险演化机理

靳泽鹏，赵江平，刘 茜

(西安建筑科技大学 资源工程学院，陕西 西安 710055)

0 引言

煤炭长时间以来在我国一次能源结构中占据重要位置，是我国最基本的能源之一，但近年来各类煤矿生产安全事故接连发生，煤矿的安全生产形势仍旧十分严峻[1-2]。近年来国内外学者专家针对煤矿安全风险演化领域展开了一系列研究，主要包括矿区生态风险演化[3]、风险-隐患-事故演化规律[4]、事故发生机理[5]和宏观演化规律[6]等。研究表明，任何事故的发生都有一个发展过程，其偶然中存在必然性。煤矿作为一个开放性复杂系统，内部风险因素众多且错综复杂，传统的线性事故风险分析方法很难反映出风险因素之间错综复杂的交互作用。耗散结构理论是研究系统耗散结构的性质及其形成、稳定和演化规律的科学，从有序和无序相互转化的机制和条件问题揭示自组织系统的机制和规律，同时耗散结构特征可将不同的风险因素进行统一的表达。因此，基于耗散结构理论研究煤矿安全风险的演化机理，可为煤矿风险预警事故演化提供理论依据。

1 煤矿系统耗散结构特征分析

耗散结构理论是研究非平衡态系统自组织现象的重要理论之一，其实质是开放、远离平衡态的系统与外界进行物质、能量、信息交换后，自发形成的新的有序状态[7]。耗散结构要求系统满足开放性、远离平衡、存在非线性作用和系统涨落4个条件。

结合以上4个条件分析煤矿安全风险演化系统的耗散结构特性。系统开放性是指煤矿安全风险不可能孤立的发生，必定存在煤矿内部间或与外部环境间物质能量的交换，同时安全风险发生后应急管理措施也会对煤矿安全风险系统施加物质和能量的交换。系统非线性作用是指，煤矿安全风险演化过程中，爆炸、火灾和瓦斯泄露等破坏性现象存在明显的非线性作用关系。系统远离平衡态分析是指在煤矿安全风险爆发前，系统处于平衡状态；由于人为或是外部环境原因打破系统的平衡状态因而造成生产安全事故，系统远离了平衡状态，此时系统正熵主导系统原理平衡态演化，系统无序程度逐渐增加。系统涨落是系统要素的独立运动或局部产生的各种运动以及在环境的干扰下系统状态变量偏离平均值的一种随机现象[8]；煤矿重大事故系统中受到人为或自然灾害等因素会产生无数“小涨落”，当涨落的影响达到一定程度时，系统会产生“巨涨落”进而造成生产安全事故。

综上，煤矿系统具有非常明显的耗散结构特征，其系统演化可利用耗散结构理论进行研究，煤矿系统安全风险演化机理概念模型如图1所示。

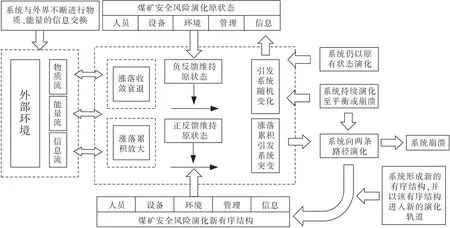
图1 煤矿安全风险演化机理概念模型Fig.1 Conceptual model of coal mine safety risk evolution mechanism

2 煤矿系统耗散结构判断模型构建

2.1 煤矿系统风险熵要素分析

熵与系统的有序度存在一定的关系，即系统的熵值越大有序程度越低；熵值越小有序度越高[9]。煤矿作为开发的复杂系统，内部风险因素错综复杂，且与外界环境具有物质和能量的交换，即系统的熵值与风险状态对应，因而有学者提出以系统风险熵表征其风险状态，以系统风险熵变表征其风险发展趋势[10]。

煤矿系统风险熵值S由2部分构成，一部分为来源于内部条件和外部环境的不可逆风险熵值(正熵)S+，另一部分则是采用人为干预等手段从外界输入改变煤矿系统风险的熵减(负熵)S-，即煤矿系统风险熵值为

S=S++S-

(1)

同时，根据熵的可加性，煤矿系统安全风险的总熵又等于人员子系统的熵SH、设备子系统的熵SE、环境子系统的熵SC、管理子系统的熵SM、信息子系统的熵SI的总和，即

S=SH+SE+SC+SM+SI

(2)

由式(1)和式(2)可得煤矿系统风险熵模型为

(3)

2.2 煤矿系统风险熵正负指标体系

为了实现煤矿系统风险熵的计算，必须建立煤矿系统风险正负熵指标体系。基于煤矿系统风险熵要素分析，按照层次分析法的思想，参考指标体系建立的相关研究[11]，构建煤矿安全风险演化系统风险正负熵指标体系，如图2所示。

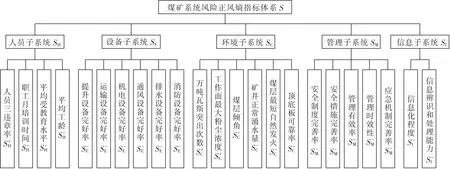
图2 煤矿系统风险正负熵指标体系Fig.2 The positive and negative entropy index system of coal mine system risk

2.3 基于熵值法的指标权重和熵值确定

计算正熵指标的比重，见式(4)

(4)

式中，A为煤矿正熵系统;xA为正熵指标所构成的矩阵。

计算正熵指标的熵值，见式(5)

(5)

上式满足0≤eAi≤1，各指标的差异系数为

gAi=1-eAi

(6)

式中，eAi为第i个正熵指标的熵值;gAi为第i个正熵指标的差异系数。

计算正熵指标的权重，见式(7)

(7)

式中，λAi为第i个正熵指标的权重。

计算正熵指标的熵值，见式(8)

(8)

式中，EA为煤矿系统的负熵熵值。

同理可得，负熵指标的权重和熵值

(9)

式中，B为煤矿负熵系统；eBi为第i个负熵指标的熵值；gBi为第i个负熵指标的差异系数;λBi为第i个负熵指标的权重;EB为煤矿系统的负熵熵值。

2.4 煤矿系统耗散结构判断模型

比利时布鲁塞尔学派提出的“布鲁塞尔器”(Brusselator)模型可作为耗散结构量化分析方法[12-13]。该模型可从系统自组织行为的发展状况来判断煤矿系统是否具有耗散结构特征并作为分析系统演化活跃性的定量依据，模型的具体表达式为

(10)

式中，EA为煤矿系统的正熵熵值；EB为煤矿系统的负熵熵值。

当式(10)<0时，煤矿系统风险熵以风险熵增为主，此时式(10)越小，风险正熵越高，煤矿风险状态越紊乱，将会向混乱无序的方向发展。当系统在外界非线性放大作用下产生“巨涨落”，煤矿系统处于状态崩溃的临界点，即使轻微的正熵输入也会导致煤矿发生状态突变，即发生事故灾难。

当式(10)=0时，煤矿系统风险熵减可抵消“微涨落”作用，即系统可以通过自组织性行为自发回到有序状态。

当式(10)>0时，煤矿系统风险熵减突破临界状态，园区内部要素通过相互作用，沿着新的自组织轨迹演化，此时煤矿安全水平不断提升，系统协同发展演化活跃性较强。

根据式(10)的描述，将式(10)的值作为煤矿系统是否达到耗散结构的定量依据，当式(10)>0时系统未达到耗散结构特征条件，当式(10)<0时系统达到耗散结构特征条件。

根据式(3)、式(7)、式(9)和式(10)得煤矿耗散结构判断模型的临界熵值为

(11)

3 实例应用

3.1 基础数据

以S省某煤矿为例，通过对该煤矿5个矿井相关资料整理和调研获取熵值计算的基础数据。根据式(4)～式(9)计算煤炭系统风险正负熵指标的权重和熵值，计算结果见表1。

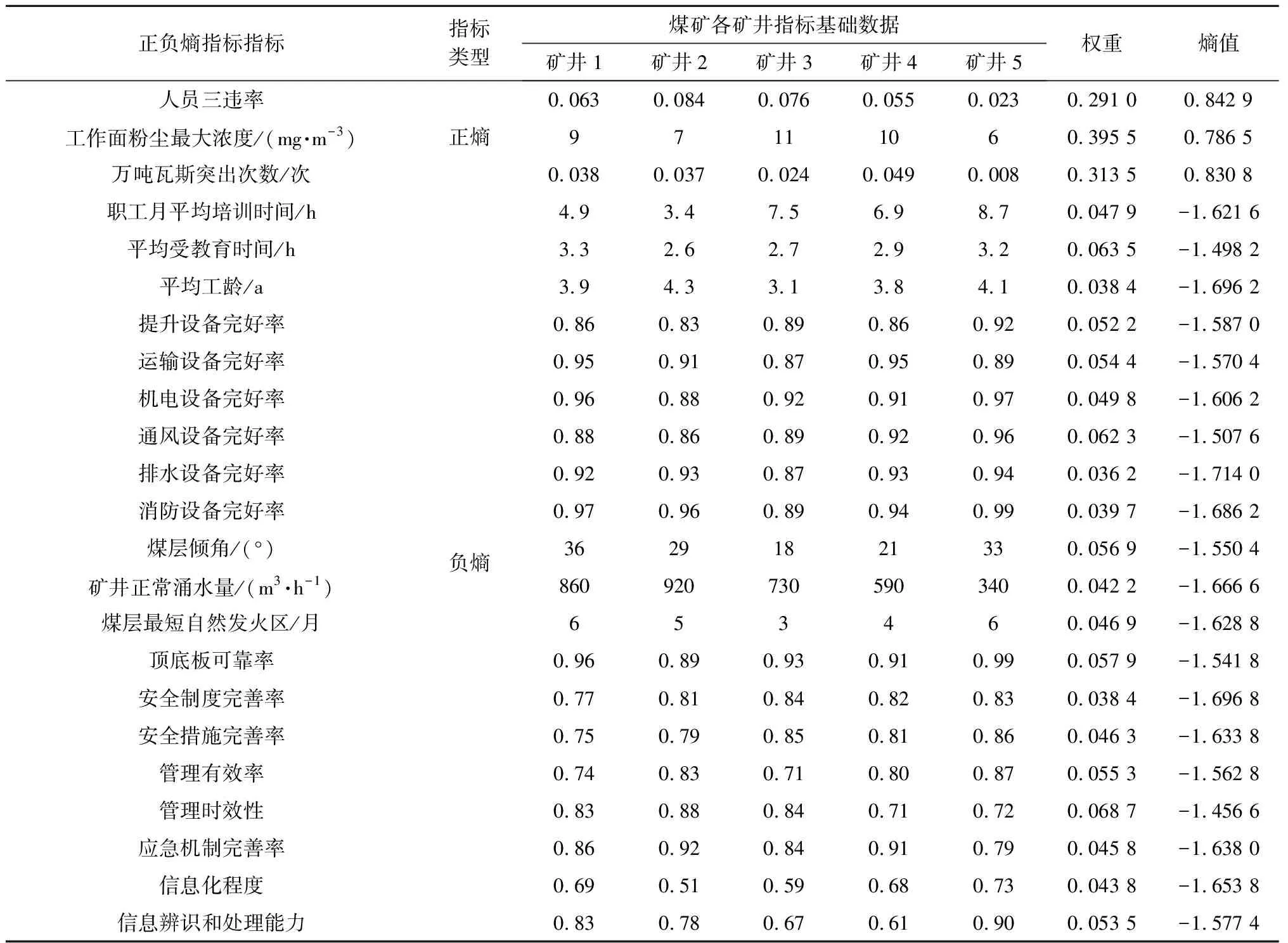
表1 指标的权重和熵值Table 1 Weight and entropy of indicators

3.2 煤矿耗散结构判断及结果分析

由表1可知，某煤矿系统风险正熵为0.816 8，负熵为-1.592 5。根据煤矿耗散结构判断模型可知，某煤矿为非耗散结构，存在一定的风险。这一结果是由该煤矿正熵偏高和负熵偏低造成的。具体来讲，造成该煤矿正熵偏高的原因为人员三违率较高，熵值为0.842 9。同时，在管理方面管理时效性负熵绝对值较低，熵值为-1.456 6；在人员方面平均受教育水平负熵绝对值较低，熵值为-1.498 2；在环境方面顶底板可靠率负熵绝对值较低，熵值为-1.541 8。

该煤矿应针对上述具体方面采取措施，降低人员三违率，提高管理时效性和顶板可靠率，同时招聘经验丰富的管理和作业人员，在抑制产生正熵的不利因素的同时，加大力度促进负熵的增长，维持煤矿系统的耗散结构并向更高、有序的程度发展。

4 结论

(1)基于耗散结构理论从系统风险熵的角度建立煤矿系统风险正负熵指标体系和煤矿系统耗散结构判断模型，分析煤矿安全风险演化机理。

(2)结合耗散结构理论分析煤矿系统耗散结构特征，从系统风险熵的角度建立煤矿系统风险熵模型并建立煤矿系统风险正负熵指标体系。

(3)利用熵值法确定指标权重和熵值，通过建立煤矿系统风险熵Brusselator模型提出煤矿成为耗散结构的判断依据，最后进行实例分析，验证模型并提出改进措施。