基于自适应优化变分模态分解的起重机故障诊断

陈洪良 李 杨 张一辉 许飞云

1江苏省特种设备监督检验研究院南通分院 南通 226011 2东南大学机械工程学院 南京 211189

0 引言

起重机是航空航天、能源和工业应用中机械设备的重要组成部分，也是起重机械系统故障诊断的主要研究对象[1]。起重机的意外故障将导致灾难性的损坏，并产生安全危险和生产力的损失。影响安全的关键系统，需要实时状态监测系统，以促进起重机故障的早期检测和诊断。声发射和振动信号分析是机械设备状态监测中常用的2种技术，它们提供了起重机在使用过程中故障状态的重要信息[2]。

在运行过程中，起重机重要部件在加载区会产生循环赫兹应力。当亚表层产生疲劳裂纹时，周围局部区域发生塑性变形，对应的应变能以100 kHz ～1 MHz的高频弹性应力波的形式得到释放[3]。利用声发射极易通过压电声换能器来采集这些能量，因为它们比不平衡、不对中和噪声等干扰低频成分高得多。在许多情况下，断层形成和起重机失效之间的持续时间很短。因此，许多研究的重点是开发先进的诊断技术，以检测早期阶段的局部故障。以裂纹形式出现的局部故障振动信号中都会产生重复的瞬态脉冲，其是对受激高频结构谐振模式的幅值调制，在频域以谐振峰旁带的形式出现[4]。这意味着传统的振动分析技术无法检测到相应的振动信号，从而很难从原始频谱中识别故障。故本文采用声发射技术对起重机重要部件进行故障信号采集以完成故障诊断任务。

利用包络分析技术对声发射信号进行解调，提取低频范围内起重机特征频率上的基波峰和谐波形式的瞬态脉冲。然而，由于恶劣的工作环境导致瞬态脉冲通常被强脉冲噪声淹没，且其他高能量成分的信号成分又与起重机故障信号相干扰，故早期提取瞬态脉冲信号比较困难。在信号处理技术的独特轨迹中，Huang等[5]引入了经验模态分解（Empirical mode decomposition，EMD）作为一种自适应时空域信号处理技术，用于分析复杂信号。该方法将原始信号分解为本征模态函数（Intrinsic mode functions，IMF）的正交分量。虽然EMD在获取起重机故障特征频率的模态方面取得了显著的成功，但其不能处理强噪声信号。同时EMD产生的另一个问题是模态混合，即信号分解过程中的模态混叠。为了克服这些问题，一些改进的EMD方法如集合经验模态分解（Ensemble empirical mode decomposition，EEMD）[6]，互补集合经验模态分解（Complementary ensemble empirical mode decomposition，CEEMD）[7]以及局部均值分解（Local mean decomposition，LMD）[8]。但这些方法仍存在模态混叠的缺点，不能有效地处理高噪声信号。

近年来，变分模态分解（Variational mode decomposition，VMD）被认为是解决上述问题的一种很有前途的方法[9]。与经典EMD相比，该方法能准确识别故障特征频率，解决信号难以分解的问题，同时避免了模态混叠问题。Zhao等[10]利用VMD的优点，将VMD技术用于行星齿轮箱的故障检测。李清等将[11]自回归最小熵反卷积和VMD相结合，从原始振动信号中提取起重机齿轮箱故障特征。应用VMD算法的一个初步步骤是定义模数k和二次乘法因子α的值。这些VMD参数控制了模态的瞬时带宽，从而减少了模态混叠问题的发生，抑制了相关模态中背景噪声的存在。Wang 等[12]采用置换熵优化（Permutation entropy optimization，PEO）算法对起重机齿轮箱信号分析进行了优化。李永波等[13]根据采样频率和齿轮啮合频率确定了IMF的个数，对行星齿轮箱进行故障识别。Zan等[14]利用瞬时频率均值图确定k发生过分解的阈值。Jun等[15]通过检测频谱分割支持边界来预测尺度空间频谱的自适应分割k值。Zhao等[16]试图通过单目标鱼群算法迭代计算α来最小化模态混叠问题，然后计算模态混合密度。这里需要注意的是，这些试验只涉及调优一个VMD参数，而猜测另一个参数的值，这在许多情况下导致信号模式分解的不足或过度。

为了自动和自适应地选择这2个参数，蒋星星等[17]开发了一种由粗到细的分解策略，利用迭代分解确定基于峭度的k值，然后利用优化算法确定平衡参数，检测轴承和齿轮箱中的故障。王志健[18]等通过最小化PSO算法中的符号动态熵（Symbol dynamic entropy，SDE）和功率谱熵（Power spectral entropy，PSE）来优化VMD参数。目前，利用人工鱼群算法、粒子群算法、蚱蜢算法、灰狼算法和甲虫天线搜索算法等多种元启发式算法进行VMD参数选择。此外，许多指标对VMD最佳参数的选择和寻找包含故障信息的相关模态如峭度、包络熵和有效加权峰度、加权峰度指数和频带熵有很大的影响。Miao等[19]对许多可以用于信号处理的稀疏性指标进行了比较，提出使用基尼系数（Gini Index，GI）作为一种不等式测度，来指导VMD等分解方法作为适应度函数，并作为模式选择的评价标准。Isham等[20]总结了VMD的研究成果，并进一步研究了最近提出的元启发式算法的潜力，为每个输入信号选择k和α的最优值。

为此，本文提出了一种基于旗鱼优化算法（Sailed fish optimizer，SFO）的自适应VMD框架，用于自动计算VMD参数的最优值。同时，将基尼系数用作一个适应度函数，以选择由SFO搜索到的最佳参数。最后，利用优化后的VMD算法，根据最大GI值确定包含故障信息的相关模式从而实现对起重机的智能故障诊断。

1 方法基础理论

1.1 VMD方法原理

VMD是由Dragomiretskiy等开发的一种先进的信号处理技术，用于将一个复杂信号以非递归的方式分解为一组拟正交的IMF。典型的VMD过程是将信号f(t)分解为若干个模态uk(t)，表示为

式中：k为模式数，uk(t)为窄带模式，其主要是调幅调频信号。

式中：Ak(t)和φk(t)为瞬时振幅和相位。所有独立模态的总和应在原始信号f(t)中使用最小二乘估计得到，其中带宽可以根据希尔伯特变换计算为

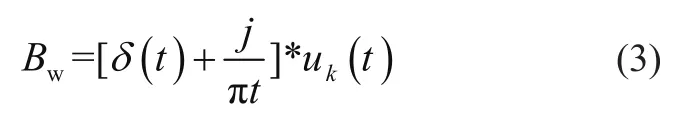
式中：δ(t)表示Dirac分布，uk(t)为第k次分解模式，j为虚部，*表示卷积算子。将指数项乘以模式uk(t)的傅里叶变换调制，并将频谱变换为相应的预估中心频带ωk，表示为

式中：{ωk}={ω1，ω2，…，ωk} 为各模态的中心频率。最后通过高斯平滑解调信号得到各模式的带宽，称为梯度L2的范数平方，表示为

如果每个模态分量具有不同中心频率的有限带宽，则目标是通过求解变分约束模型的框架，利用式（6）使每个模态分量的带宽估计的总和最小化。

将二次惩罚因子α和拉格朗日乘子λ应用于式（6），将优化问题由有约束形式转化为无约束形式。故得到增广拉格朗日函数表示为

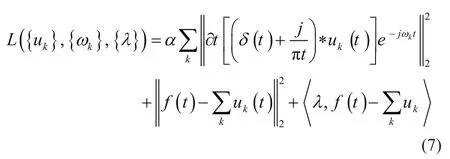
利用交替方向乘子法改变各分量及其中心频率来求解问题并找到最优解。且模态uk和中心频率ωk更新为

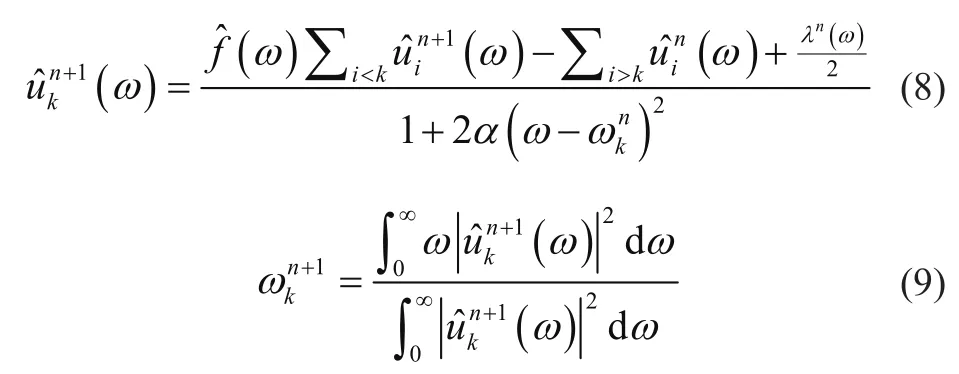
1.2 SFO方法介绍

SFO是Shadravan等[21]最近提出并开发的一种新的元启发式算法，用于解决工业随机问题。其灵感来自于旗鱼家族的海洋动物行为，以及旗鱼群体作为捕食者如何协调智能狩猎策略，以捕食尽可能多的沙丁鱼。该算法还精确地模拟了沙丁鱼群如何改变位置和策略以逃避捕食者。与其他群智能算法相比，SFO算法在探索开发阶段具有一定的竞争力，在达到全局最优的速度较快，同时避免了大量的局部最优点。SFO测试了6种最先进的元启发式算法，如灰狼优化、粒子群优化、缎子园丁鸟优化器、蚁狮优化器、Salp群算法和遗传算法，并使用一组单模态和多模态(高维)基准函数进行比较。

由文献[22]的结果表明，SFO算法比其他算法收敛速度更快，尤其对于多模态函数即大规模全局优化，将获得更好的解，且SFO对于多模态基准函数具有更好的探索和开发阶段性能。受其避免局部最优能力的启发，Hamouti等[23]应用了该算法的改进版本来解决集装箱港口的泊位分配规划问题。

1.3 基尼系数（GI）介绍

GI是一种统计不等式指标，近年来被广泛应用于机械设备故障诊断。它是一种比峭度和相关峭度更有效的检测重复脉冲的准则，是信号处理技术中可靠的检测方法。GI值在[0, 1]范围内，对区分低值和高值具有较高的敏感性，表示为

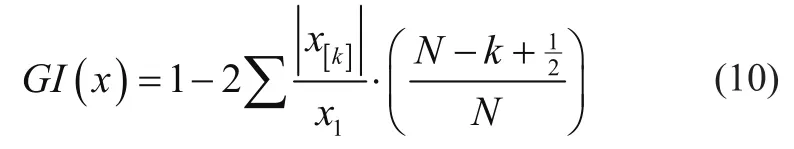
对于一个向量x=[x(1)，x(2)，…，x(N)]，其可以通过x[k](k=1，2，…，N)来重新对元素进行排序表示，其中x1表示x的l1范数。

2 所提出的自适应优化VMD方法介绍

2.1 所提方法的具体步骤

所提方法利用SFO和GI作为适应度函数来自适应选择VMD参数。流程图步骤如图1所示。

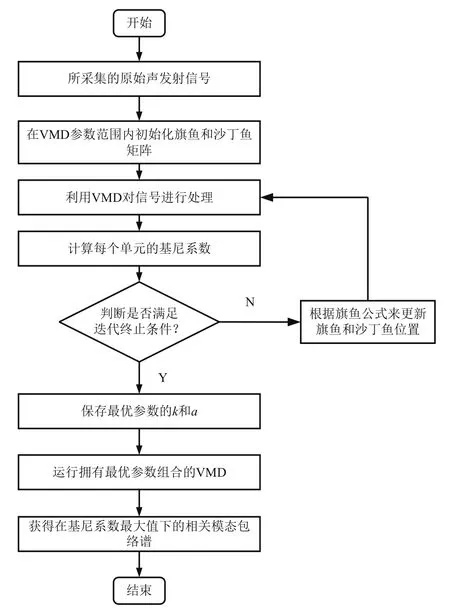
图1 所提方法的流程图

1）将有缺陷的起重机重要部件声发射信号输入到VMD算法。

2）根据k和α的预定义范围，为SFO算法中的每个元素生成参数k和α的随机值。

3）对原始声发射信号导入经过SFO处理后的VMD来进行处理。

4）对于每一次VMD分解迭代，根据式（10）来确定所得模态包络的GI值，并选择最大GI值所对应的模态。

5）根据每次迭代的单元值以获得更好的结果，直到达到终止条件。选择产生最大GI的值作为最佳参数。

6）利用最优k和α值的VMD来分解信号，选择GI最大值包含故障信息的相关模态。

7）分解过程完成后，在方波包络谱和时域中对相关模态进行分析。

2.2 参数设置

为了减少计算时间，本文选取的旗鱼种群和沙丁鱼种群分别为5和25。当旗鱼单元捕获所有的沙丁鱼或者迭代周期达到20时，将会出现终止条件。本文将最大迭代次数设置为20。VMD方法的效率取决于模数k、二次惩罚因子α、二次上升时间步长τ、初始ω和容差Δ5个关键参数的选择。参数ω、τ和Δ的推荐值与文献[24]中原始工作的推荐值一致。例如，Δ被设置为1×10-9，且ω被初始化为0。通过文献[24]可知，若精确重建不是强制性的，则只考虑二次惩罚因子而忽略拉格朗日乘子是合适的选择。因此，τ的值被设为零，以有效地关闭拉格朗日乘子。算法的设计是在2个种群集[2, 12]和[10, 10 000]中寻找k和α的最优值，这2个群体的选择是从累积的许多以前的著作中获得的共同范围。此外，增大模态范围会导致计算时间过长和结果冗余，且k和α的值通过SFO来进行优化。

3 实验设置

为了验证所提方法的有效性，首先选用SAMOS声发射采集系统来采集本文所选的MQ1260-45型桁架式门座起重机的声发射信号。由于复杂的工作环境和投入使用的时间较长，所选起重机的重要部件，如：人字架两侧拉杆、臂架根部弦杆、转台大梁局部狭窄等区域均出现了明显的开裂和损伤。本文总体的实验过程如图2所示，实验采用了7个声发射传感器通过声耦合剂来完成起重机7个重要部件的声发射信号采集。其中7个重要部件分别为：旋转柱、A -框架、吊货臂、龙门腿、塔身、旋转平台梁以及配重。同时，在声发射信号采集过程中的所有参数设置如表1所示。更重要的，本文选择从龙门腿采集到的声发射信号来对本文所提方法进行验证，其原始声发射信号包括：时频域波形和包络谱，如图3所示。由图可知，无论是时域还是频域都没有提取出有用的信息。如图3c所示的包络谱，噪声和其他频率分量对缺陷频率的干扰较大，故无法识别出故障特征。

图2 实际工程应用中的起重机声发射数据采集

图3 采集于龙门腿的原始声发射信号

表1 起重机声发射信号采集参数设置

4 诊断结果分析

将SFO和GI的最大值作为目标函数应用于VMD，得到k和α的优化值（即k=8和α=100），其收敛曲线如图4所示。然后，利用拥有最优值k和α的VMD对原始声发射信号进行分解，从而获得如图5所示的分解结果，其中包括时域波形和频域谱图。此外，从表2的结果来看，第3阶模态的GI值最高，故认为是最相关的模态进行分析。图6a和图6b分别为第3个模态的时域和包络谱，由图可知，原始故障声发射信号的瞬态脉冲获得了极大的降噪和滤波。此外，包络谱显示了所采集龙门腿声发射信号的故障频率。

图4 原始龙门腿声发射信号的最大GI值的收敛曲线

图5 原始信号的VMD分解结果

表2 利用所提方法得到的VMD各分解模态的GI值

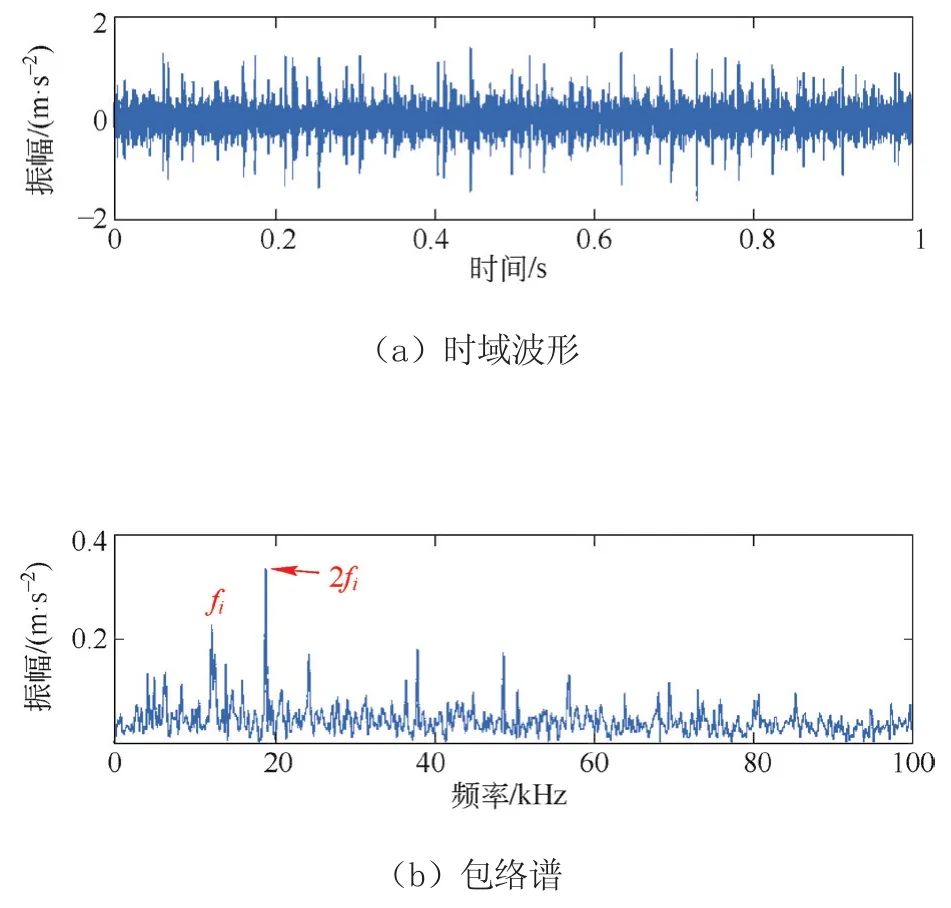
图6 经过所提优化VMD方法重构后的信号

为了验证所提方法的优越性，将所提出的优化VMD方法与LMD和EEMD进行对比，其分解结果如图7所示，阐明了各种方法在噪声环境中提取故障特征频率的有效性。由图7a所示的LMD分解结果可知，在故障基频fi处有峰值且只存在1个谐波频率2fi。然而，LMD得到的包络谱频率也受背景噪声和其他频率的影响造成分析的混乱。图7b给出了采用所提优化VMD方法的相关分解结果，其中k=8，α=100。在基本故障频率fi处存在2个谐波的峰值，由此表明所提方法在信号模态分解和噪声消除方面的有效性。图7c中的EEMD产生的包络谱也只存在1个谐波频率，且噪声干扰明显。为了进一步定量比较，表3显示了每种方法的GI值和故障特征系数。由表3可知，所提自适应优化VMD方法的GI和故障特征系数值均最高。更重要的，与LMD和EEMD相比，所提方法是消除噪声和提取故障特征最有效的方法。

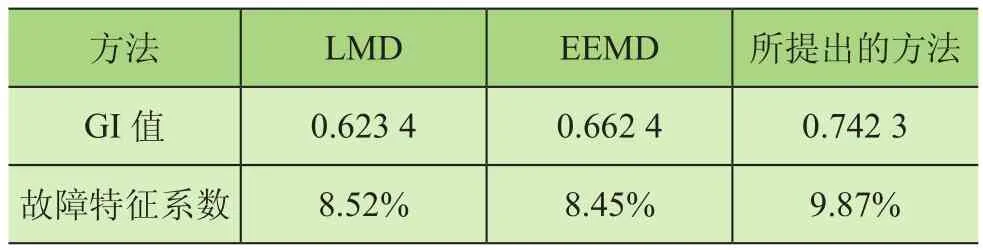
表3 采用3种方法得到的GI值和故障特征系数

图7 不同方法得到的包络谱

5 结论

本文提出了一种基于旗鱼优化算法和基尼指数准则的自适应变分模态分解方法。该方法引入了一种自动选择最优VMD参数的方法，在克服起重机声发射信号中噪声干扰的同时，有助于故障相关模态的选择，利用来自实际工程中采集的起重机重要部件的声发射信号验证了所提方法的有效性。结果表明，所提方法能有效、高效地找到包含故障信息的相关模态，通过与EEMD和LMD对比可知，所提方法在识别基频和谐波的同时，能最大限度地消除噪声。同时与所对比方法的模态相比，所提方法各模态的GI值和故障特征系数都较高，从而验证了所提方法在起重机故障诊断中优越性。