基于改进领航-虚拟跟随法的车辆队列控制

杨 强 袁希文 肖绯雄 罗佳祥,3

1西南交通大学牵引动力国家重点实验室 成都 610031 2中车株洲电力机车研究所有限公司 株洲 412001 3西南交通大学电气工程学院 成都 611756

0 引言

车辆队列行驶较单车行驶具有降低燃油消耗和减小空气污染，增加道路交通的容载量等优点。随着汽车智能驾驶技术的不断发展完善，无人车辆队列控制技术逐渐成为近年国内外研究的热门课题之一[1]。目前队列控制方法主要有行为法[2，3]、人工势场法[4，5]、虚拟结构法[6，7]和领航-跟随法[8-10]。领航-跟随法是目前无人系统编队控制中最常用的方法[1]。领航者是编队中被指定的某一车辆，其他车辆通过获取领航者的运动信息来规划自身的运动轨迹并进行控制从而达到追踪领航者的目的[11]。领航-跟随法使得队列控制问题成为传统轨迹跟踪问题的自然延伸，在通过领航-跟随法确定跟随车需要跟踪的特定位置后便可将汽车智能驾驶中的纵向控制与横向控制[12-15]技术运用于其上，从而实现车辆队列控制。

王保防等[16]根据车式移动机器人的运动学模型提出了一种基于轨迹跟踪多机器人队列控制方法，利用队列结构参数确定队形，根据队列轨迹和相关参数生成虚拟机器人；然后运用反步法构造车式移动机器人轨迹跟踪系统的李雅普诺夫函数，通过使该函数负定，得到跟随机器人的轨迹跟踪控制器。罗京等[17]针对多个两轮差动移动机器人的队列控制问题，提出了一种结合Polar Histogram避障法的领航-跟随协调队列控制算法。该算法在领航-跟随l-φ队列控制结构的基础上引入虚拟跟随机器人，采用极坐标系下基于障碍物密度的Polar Histogram避障法，引导多机器人队列智能地避开障碍物。师五喜等[18]为控制多轮式机器人协作系统中跟随者机器人的输入速度v和加速度a不超过其额定值vm和am，设计了一种速度和加速度受限的领航-跟随型编队控制算法，此算法设计了2个一阶滤波器，作为控制器的2个反馈信号，且此反馈信号及其导数的大小受限于2个滤波器参数。

上述文献的共同特点是在领航-跟随l-φ队列控制结构的基础上引入虚拟跟随车而变成领航-虚拟跟随法，将队列控制问题转化为跟随车对虚拟跟随车的轨迹跟踪控制，进而设计了不同的算法进行控制器的设计。然而这种使虚拟跟随车参考航向角等价于领航车的航向角的方法，在曲线工况下存在模型误差。

因此，本文提出了一种考虑跟随车参考路径点连线与横轴的夹角作为参考航向角的改进领航-虚拟跟随方法规划跟随车位姿，提出基于运动学模型的预测方法规划跟随车速度。分别使用PD控制和误差修正的Stanley方法[19]控制车辆油门、刹车达到跟随车参考速度和跟随车前轮转向使其达到参考轨迹。最后使用CarSim/Simulink仿真验证了本文提出的方法较改进前方法的队列控制横向跟踪效果的提升。

1 车辆队列运动规划

车辆队列运动规划是在领航车位姿、速度确定的条件下，为跟随车横向控制设计参考轨迹使跟随车与领航车保持特定的队形；为跟随车纵向控制规划参考速度使领航车与跟随车的距离稳定在参考距离。本文通过改进的领航-虚拟跟随法规划跟随车轨迹，基于车辆运动学模型预测方法规划跟随车速度。从使用领航车信息进行队列运动规划到队列控制实现的过程如图1所示。

图1 车辆队列控制原理框图

1.1 改进的领航-虚拟跟随法

领航-虚拟跟随法即设置与领航者一定距离和角度的虚拟车辆作为虚拟跟随车，当控制跟随车与虚拟跟随车的位置完全重合时便实现了车辆编队。如图2所示，可得虚拟跟随车车辆位姿为

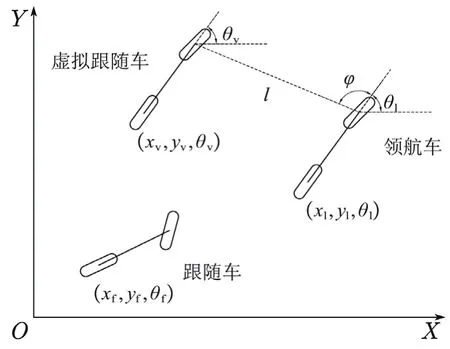
图2 领航-虚拟跟随法队形结构

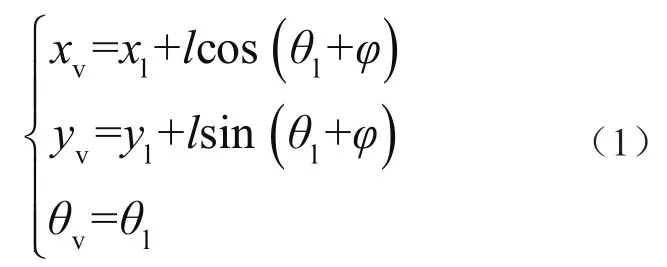
式中：xl、yl分别为领航车前轴中心在全局坐标系下横坐标、纵坐标位置，θl为领航车航向角，xv、yv分别为虚拟跟随车前轴中心在全局坐标系下横坐标、纵坐标位置，θv为虚拟跟随车航向角，l、φ分别为跟随距离和跟随角度。

由式（1）可知，虚拟跟随车在其轨迹中的参考航向角等于对应位置领航车的航向角，但并不一定是其轨迹的切线与横轴的夹角。如图3所示，以跟随车作圆周轨迹运动的特例来说明。领航车的参考航向角为圆周离散点切线与横轴X的夹角θl。参考航向角设定的依据为刚体瞬时速度的方向沿运动轨迹的切线方向，以运动轨迹切线与横轴的夹角作为车辆的参考航向角[20，21]。

图3 领航-虚拟跟随法轨迹

考虑图3中领航车位置处于A点而虚拟跟随车位置由式（1）确定而处于B点，由领航-虚拟跟随法确定的参考航向角为θl，而跟随车轨迹切线与横轴的夹角为θl2，由于这2个角度不相等，跟随车从理论上无法精确地跟随参考轨迹，即领航-虚拟跟随法在这种特定的情况下存在模型误差。

因此，通过使虚拟跟随车参考航向角等于2个时刻虚拟跟随车位置的连线与横轴的夹角以近似其位置切线与横轴的夹角，给出改进的领航-虚拟跟随法表达式为

式中：xl(k)、yl(k)分别为此刻领航车前轴中心在全局坐标系下横坐标、纵坐标位置，θl(k)为此刻领航车航向角，xv(k)、yv(k)，xv(k-1)、yv(k-1)分别为此刻和上一时刻虚拟跟随车前轴中心在全局坐标系下横坐标、纵坐标位置，θv(k)为跟随车航向角，l、φ分别为跟随距离和跟随角度。

1.2 纵向速度规划

如图4所示，此时刻领航车的位置、航向角、速度和车轮旋转角度已知，跟随车的位置、航向角、车轮旋转角度已知，速度为待求量。该模型假定车辆在未来一个短的时间内以恒定速度运动且车轮转角不变。在速度约束条件下，当求解某一速度使得2车前轴中心距离与参考距离最接近，此速度即为跟随车的参考速度。

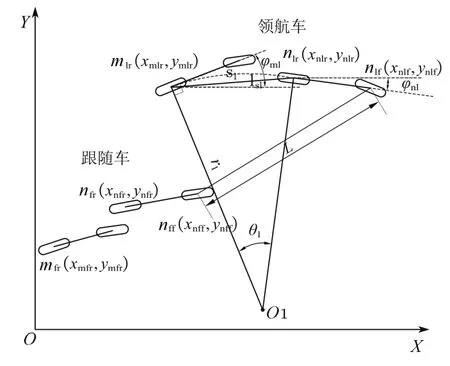
图4 领航车、跟随车运动学模型预测方法几何分析

由阿克曼转向模型有

式中：δl为领航车车轮转角，rl为领航车转弯半径，a为领航车轴距。

经过时间t，车辆运动距离为

式中：sl为领航车位移（图中虚线表示的一段圆弧），vl为领航车速度。

由阿克曼转向模型与平面几何关系有

式中：lsl为领航车2时刻车辆后轴中心距离。

根据运动学模型，有

式中：θl为领航车运动变化角。

领航车t时刻后车辆后轴中心位置为

式中：xmlr、ymlr分别为领航车后轴中心当前时刻在全局坐标系下的横坐标、纵坐标，xnlr、ynlr分别为领航车后轴中心未来时刻在全局坐标系下的横坐标、纵坐标，φml为当前时刻领航车车身航向角。

领航车t时刻后车辆前轴中心位置为

式中：xnlf、ynlf分别为领航车前轴中心未来时刻在全局坐标系下的横坐标、纵坐标，φnl为未来时刻领航车车身航向角。

同理可得跟随车t时刻后车辆前轴中心位置(xnff，ynff)。

2车前轴中心距离为

求解式(11)即得到跟随车参考速度使得未来一个时刻后2车前轴中心距离与参考距离最接近。

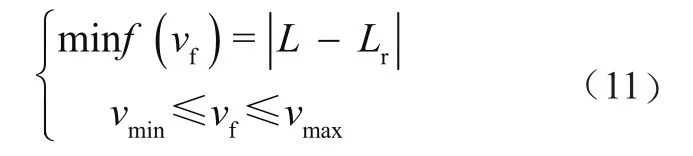
式中：L为2车前轴中心距离，Lr为期望领航车与跟随车所保持的参考距离，vf为待求的跟随车速度，vmin和vmax为跟随车所允许的最小速度与最大速度。

2 车辆队列运动控制

跟随车队列运动控制器的设计包含转向角横向控制和速度纵向控制，2个方面的内容，转向角横向控制为当跟随车的参考位姿由领航-虚拟跟随法确定后，使用误差修正的Stanley方法进行横向控制使跟随车处于参考轨迹上。速度纵向控制为当跟随车参考速度由规划得到后，使用标定策略对车辆驱/制动非线性环节拟合与PD控制跟随车速度达到参考速度。

2.1 转向角横向控制

本文使用误差修正的Stanley方法对跟随车辆转向进行控制。如图5所示，其基于前轴中心点与参考轨迹的几何关系给出非线性的前轮转向角控制量，其转角表达式为

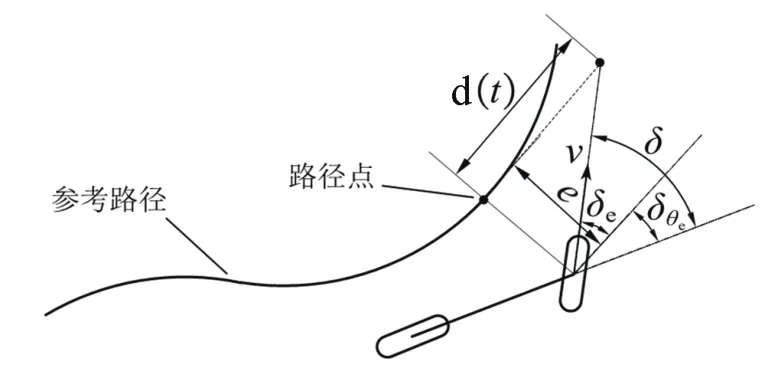
图5 Stanley方法几何分析

式中：δθe为航向角（近似等于车身与横轴的夹角）误差引起的前轮转向角，可由当横向误差为0时求得，用以消除航向角误差；δe为横向误差（前轴中心与参考轨迹的最近距离）引起的前轮转向角，可由当航向角误差为0时求得，用以消除横向误差；φ为跟随车航向角；φr为参考航向角；v(t)为跟随车速度；e(t)为横向误差；k为比例系数。

前轮转向角为

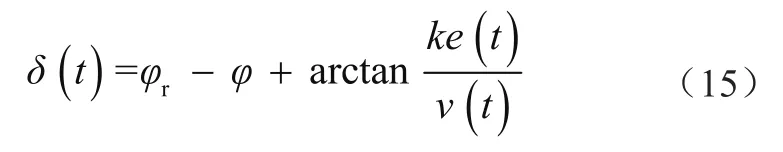
若将Stanley方法直接应用于车辆队列控制问题中的跟随车时会出现误差距离不匹配的问题。Stanley方法的路径点是通过索引车辆前轴中心点与参考轨迹的最近点，将其作为路径点，将2点之间的距离作为误差距离，车轮转角将使得误差距离趋于0。跟随车的路径点由虚拟跟随车的位置决定，当虚拟跟随车与跟随车位置如图6所示时，Stanley方法中的横向误差若直接使用2车距离即图5中e所示距离，相当于将虚拟跟随车与跟随车的纵向距离误差也进行了考虑使得横向误差过大，会出现转向过大的问题。此时计算转角误差应当使用2点距离在路径点切线的垂直方向投影替代，即图6中elat所示距离。

图6 误差修正的Stanley方法几何分析

因此，跟随车横向控制转角为

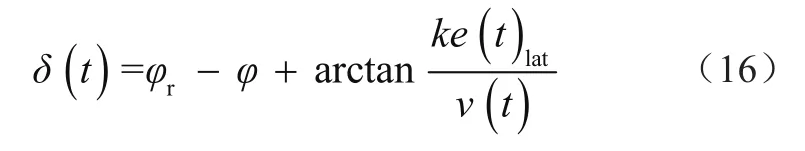
2.2 速度纵向控制

车辆队列控制问题中跟随车纵向控制的过程是在对车辆驱/制动非线性环节拟合的基础上，将由PD控制得到的车辆期望加速度转化为油门/刹车信号控制车辆实际速度达到规划得到的参考速度，以保持跟随车与领航车的距离恒定。

首先通过开环标定的策略拟合车辆驱/制动非线性环节。其过程是在Carsim中选择平直道路，在不同油门开度和刹车压力输入的情况下，对车辆速度、加速度数据进行多次采集，并将数据拟合生成三维标定表。标定结果如图7所示。使用车辆驱/制动标定表时是以期望加速度、车速作为输入，以油门开度/制动压力作为输出，其关系表示为

图7 驱/制动标定表

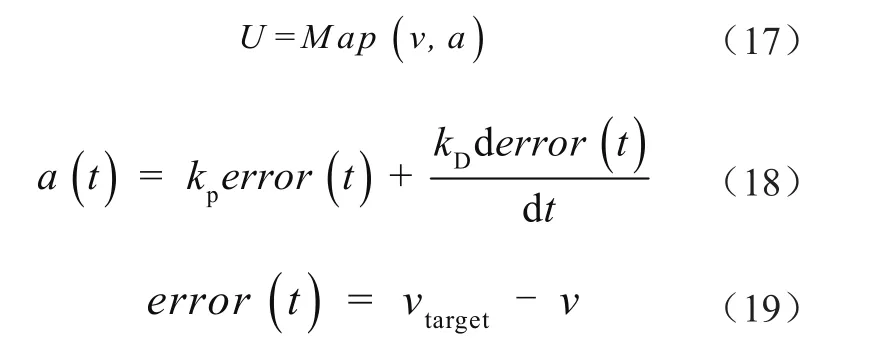
式中：U为开环油门开度/制动压力；(Map)为标定表；v为车辆速度；a为车辆期望加速度；kp为比例系数，取值为6；kD为微分系数，取值为0.05；error(t)为期望速度与车辆实际速度之差；vtarget为期望速度，v为车辆实际速度。

3 仿真实验与分析

在CarSim/Simulink中，分别使用领航-虚拟跟随法与本文所提的参考航向角表达式修正后的领航-虚拟跟随法对车辆进行三角形编队仿真。仿真所使用的车辆为Carsim数据库中自带的B级Hatchback轿车。其车身质量为1 230 m/kg；质心到前轴距离a为1 040 mm；质心到后轴距离b为1 560 mm；质心高度h为540 mm；轮距L为1 480 mm；车身绕z轴转动惯量IZ为1 343.1kg/m2；轮胎类型为185/65R15。

仿真的初始条件设置为：领航车辆行驶的轨迹分别为圆心位置（0 m，25 m）、半径为25 m的圆周和由方程y=4sin(x/10)确定的正弦曲线。领航车初始位置为（0 m，0 m），速度为10 m/s匀速；跟随车辆1、2初始位置分别为（-4.85 m，2.8 m）、（-4.85 m，-2.8 m），初始速度为10 m/s；2台跟随车前轴中心与领航车前轴中心参考距离都为5.6 m。

3.1 改进前、后领航-虚拟跟随法仿真结果对比

改进前、后领航-虚拟跟随法在圆周和正弦曲线下车辆队列控制仿真的轨迹如图8、图9所示。轨迹图中车辆位置为从0时刻开始每隔1.5 s取样确定的。由图可知，改进前、后的领航-虚拟跟随法均可以引导跟随车使其与领航车形成预定的三角形编队，但领航-虚拟跟随法下跟随车辆偏离参考轨迹的横向距离较大，改进后的领航-虚拟跟随法下跟随车辆偏离参考轨迹的横向距离较小。图10、图11分别展示了圆周工况下改进前、后领航-虚拟跟随法下的3车车轮转角与车辆速度。图12、图13分别展示了正弦曲线工况下改进前、后领航-虚拟跟随法下的3车车轮转角与车辆速度。如图14、图15所示的改进前、后领航虚拟跟随法在圆周和正弦曲线下的横向误差，可知改进后的领航-虚拟跟随法使得跟随车横向跟踪误差得到了较大的降低。

图8 圆周工况下车辆轨迹

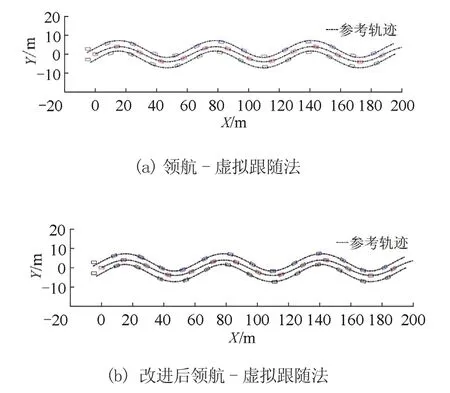
图9 正弦曲线工况下车辆轨迹

图10 圆周工况下车轮转角

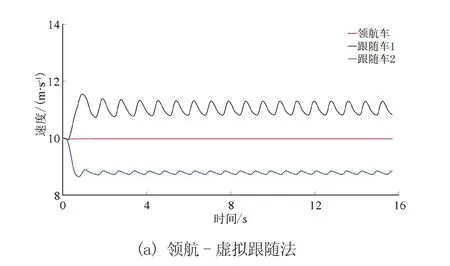
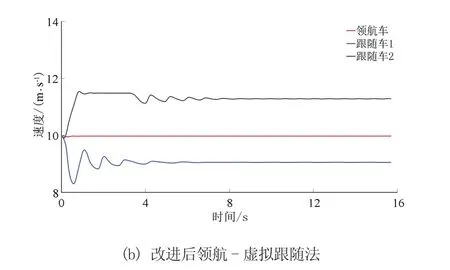
图11 圆周工况下车辆速度

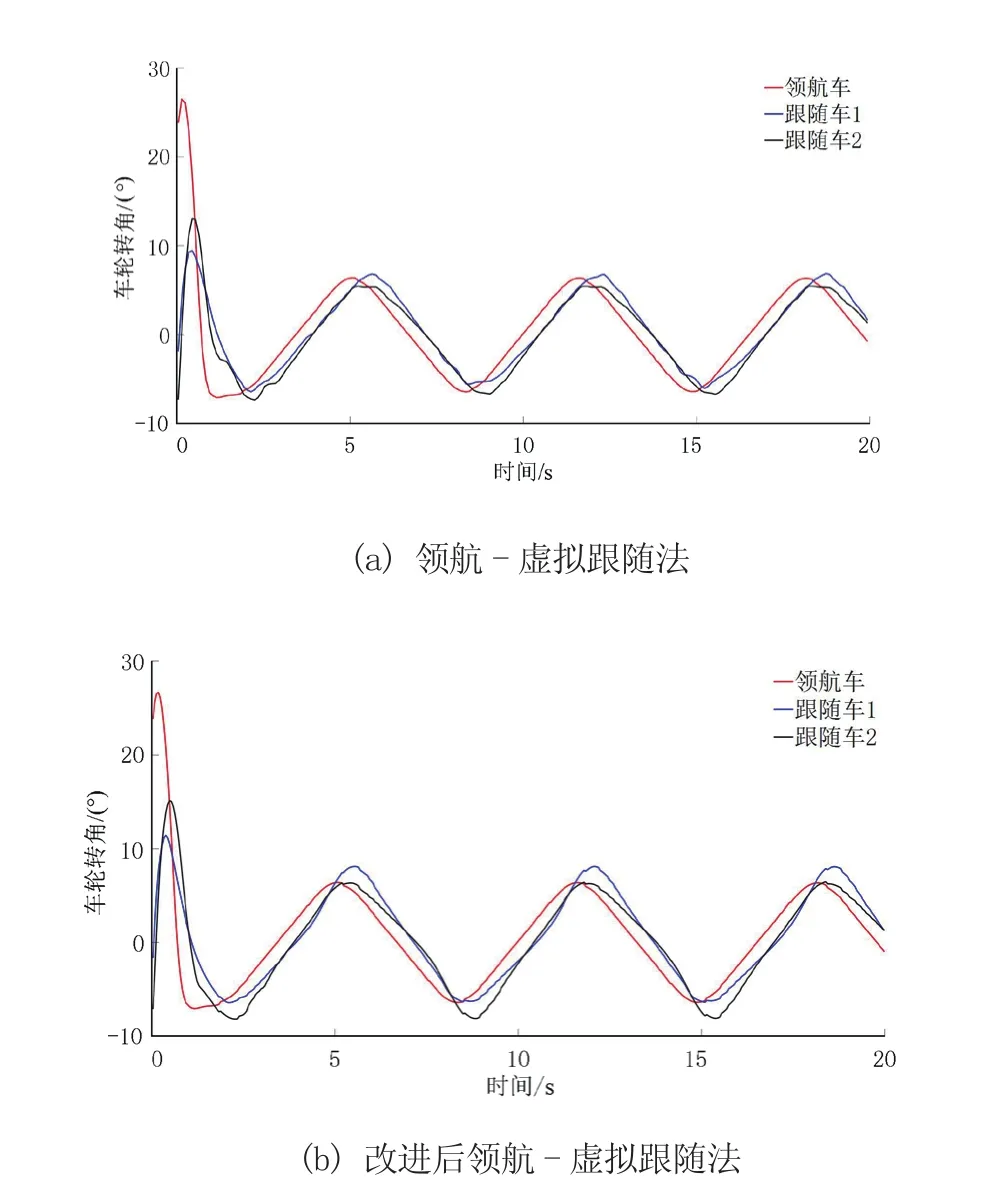
图12 正弦曲线工况下车轮转角

图13 正弦曲线工况下车辆速度

图14 圆周工况下横向跟踪误差

图15 正弦曲线工况下横向跟踪误差

3.2 仿真结果分析

改进前、后的领航-虚拟跟随法在圆周和正弦曲线下跟随车横向跟踪误差如表2、表3所示。其中，表2中误差均值通过各时刻误差绝对值求和平均后得到。表3中，因初始位置关系所造成的误差最大值无意义因此不计，误差最大值选取的是0.57以后的误差绝对值的最大值。

表2 圆周工况下横向跟踪误差

表3 正弦曲线工况下横向跟踪误差 m

从结果来看使用本文所提的参考航向角公式修正后的领航-虚拟跟随法在圆周曲线、正弦曲线工况下横向误差均值和最大值均较改进前降低。在圆周工况下跟随车1号、2号横向误差均值较改进前分别降低了0.486 m与0.339 m，降低幅度为83.22%、69.61%；横向误差最大值较改进前分别降低了0.445 m、0.339 m，降低幅度为74.92%、67.26%。在正弦曲线工况下跟随车1号、2号横向误差均值较改进前分别降低了0.231 m与0.232 m，降低幅度为73.80%、70.09%；横向误差最大值较改进前分别降低了0.407 m、0.405 m，降低幅度为70.66%、70.31%。

改进后的领航-虚拟跟随法能使跟随车横向跟踪误差降低的原因是传统的领航-虚拟跟随法以领航车的位置通过几何关系确定虚拟跟随车位置后，直接以领航车的航向角等于虚拟跟随车的航向角。航向角是车辆速度方向与横轴的夹角，车辆速度方向为车辆运动轨迹的切线方向。当虚拟跟随车的位置确定即跟随车行驶的参考路径确定后，其参考航向角即已确定，此时强行令其等于领航车的航向角反而会产生模型的误差，降低了横向跟踪的精度。改进后的领航-虚拟跟随法能够较大地提高曲线工况下跟随车横向跟踪精度。横向误差将影响到车辆对车道限界的遵守，跟随车横向跟踪精度的提升有助于提高其运行安全性。

4 结语

本文在领航-虚拟跟随法的基础上修改了虚拟跟随车航向角的表达式，提出了基于车辆运动学模型的预测方法规划跟随车速度，分别通过误差修正的Stanley方法和PD方法进行横向、纵向控制，通过Carsim/Simulink联合仿真平台对改进前的领航-虚拟跟随法和本文所提方法进行了圆周和正弦曲线工况下的对比。结果显示在圆周工况下跟随车1号、2号横向误差均值改进后较改进前降低了83.22%、69.61%；横向误差最大值降低了74.92%、67.26%。在正弦曲线工况下跟随车1号、2号横向误差均值改进后较改进前降低了73.80%、70.09%；横向误差最大值降低了70.66%、70.31%。相比较于传统的领航-虚拟跟随法，改进的领航-虚拟跟随法能够较大地提高车辆队列控制中跟随车在曲线工况下的横向跟踪精度。