共母线OW-PMSM驱动系统改进SVPWM算法研究

王 恒

（江苏大学电气信息工程学院，江苏镇江 212013）

0 引言

开绕组永磁同步电机（Open Winding Permanent Magnet Synchronous Motor，OW-PMSM）作为一种新型的电机拓扑结构，拥有传统PMSM 结构简单、功率密度高和运行效率高的优点［1-2］。同时，双逆变器的驱动形式能够提供更大的直流母线电压，保证了电机在宽调速范围的恒转矩运行，且降低了单个逆变器的容量负担［3］。目前，根据OWPMSM 双逆变器所接母线电源的不同，其拓扑结构有共母线、隔离母线和飞跨电容［4-6］。其中，共母线OW-PMSM 驱动系统仅需单个直流电源供电，减小了系统的体积、重量和成本，极其适用于高压大功率电驱场合［7］。但是，共母线拓扑的零序电流回路导通，相电流中存在的零序电流会影响电机的驱动控制［8］。

驱动OW-PMSM 的双逆变器系统在矢量调制过程中会输出一定的共模电压，其作为零序回路中的零序电压造成了零序电流的出现［9-10］。为了抑制零序电流，文献［11-13］通过选取双逆变器中不产生零序电压的开关组合参与矢量调制过程，虽然对零序电流有一定抑制效果，但损失了开绕组拓扑母线电压利用率。文献［14-15］在保证开绕组拓扑母线电压利用率的前提下调整零电压矢量作用时间，使单个控制周期内的平均零序电压为零，但其两次扇区判断过程增加了计算负担。

因此，本文针对共母线OW-PMSM 驱动系统，提出了一种改进的SVPWM 算法。通过调制过程中选择特定的零电压矢量，最大程度地利用了直流母线电压，且借助其产生的零序电压抑制了OW-PMSM 相电流中的零序电流。最后，基于MATLAB/Simulink 环境搭建共母线OW-PMSM驱动系统，验证本文所提算法的有效性。

1 OW-PMSM 数学模型与矢量分析

1.1 OW-PMSM 的数学模型

OW-PMSM 是在传统PMSM 基础上将定子绕组Y 型中性点打开后而形成，本质上仍然是个高度耦合、结构复杂的非线性系统。为简化电机仿真模型建立和系统驱动控制研究，必须应用相应的坐标变换对原始数学模型进行变量解耦和降阶变换，通常采用基于永磁体磁场定向的两相旋转dq0 坐标系［16］。OW-PMSM 在两相旋转d-q坐标系下的电压方程和电磁转矩方程分别为：

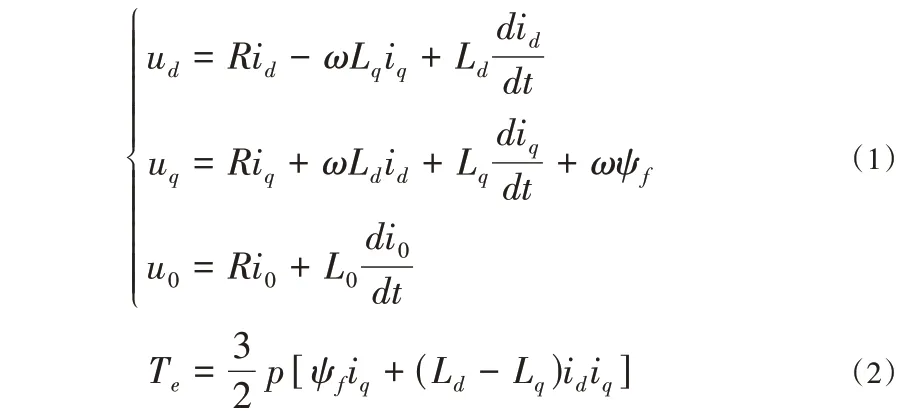
其中，ux、ix、Lx（x=d，q，0）分别表示电机在dq0坐标系中的定子电压、电流和电感分量；ω为电机转子的电角速度；ψf为电机转子永磁体磁链；p为电机的极对数。

同时，OW-PMSM 的机械运动方程为：

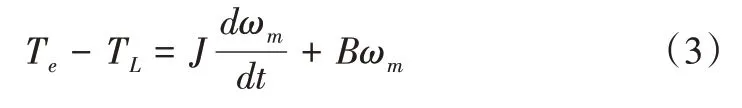
其中，TL为负载转矩；J为转动惯量；ωm为机械角速度，且ωm=pω；B为粘滞系数。

1.2 双逆变器电压空间矢量分析

共母线OW-PMSM 打开的绕组由双逆变器共同驱动，其拓扑结构如图1 所示。逆变器INV1 和INV2 共用一个直流电压源，分别输出电压矢量到OW-PMSM 中，合成相应的参考电压矢量［17］。

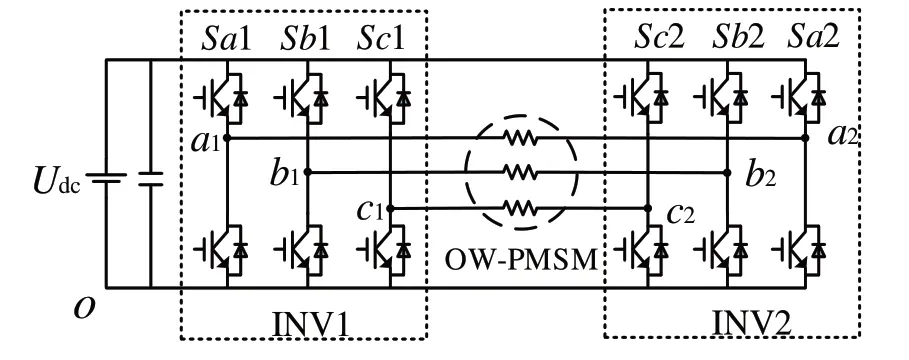
Fig.1 Common bus OW-PMSM drive system topology图1 共母线OW-PMSM 驱动系统拓扑

图中Sx1 和Sx2（x=a、b、c）分别表示INV1 和INV2 的3对功率开关器件。为避免直流电压源短路，上下管只能对称通断。记上管导通为“1”下管导通为“0”，双逆变器各自输出的电压矢量可表示为：

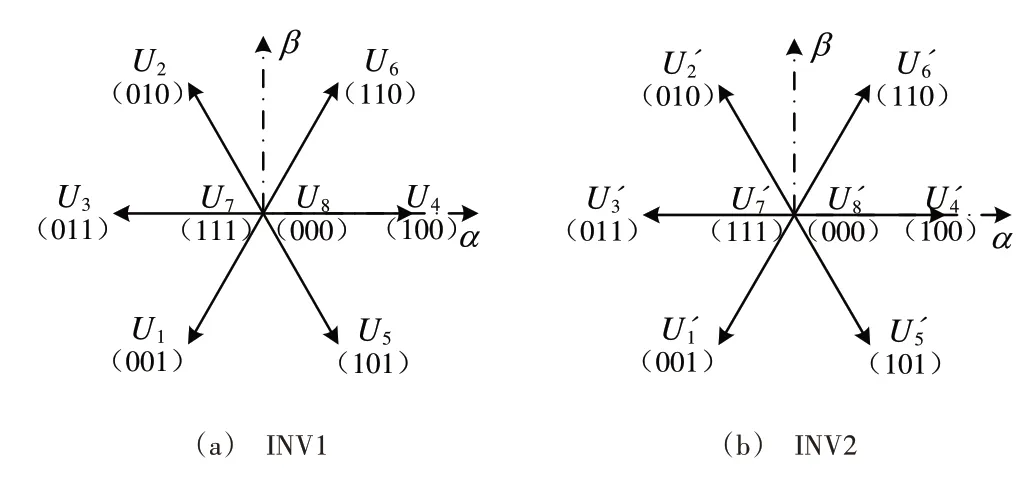
Fig.2 Voltage vector distribution of INV1 and INV2图2 逆变器1和逆变器2电压矢量分布

同时，在OW-PMSM 系统中的合成电压空间矢量Us，由双逆变器输出的电压空间矢量作差得到。根据矢量的合成规则得到共64 个电压矢量，它们在空间中的分布如图3 所示。剔除相同的矢量后可得到18 个非零电压空间矢量和1 个零电压空间矢量，其电压幅值大小有4/3Udc、2/和0。

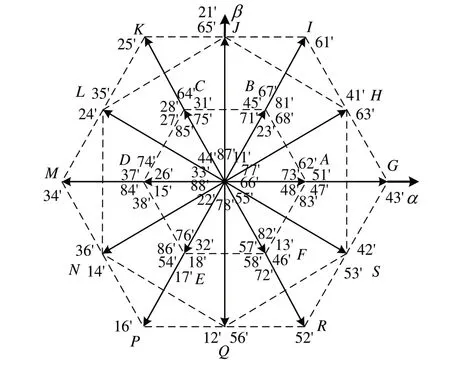
Fig.3 Voltage space vector distribution of dual inverter system图3 双逆变器系统电压空间矢量分布

观察电压矢量分布，能够构建类似单逆变器驱动系统输出的正六边形基本电压空间，3 个大中小正六边形GIKMPR、HJLNQS 和ABCDEF。类似于传统SVPWM，每个六边形基本电压空间矢量都可进行矢量调制，产生同步旋转的空间磁场。同时，定义最大调制系数ηmax为逆变器系统能够输出的最大不失真电压的幅值Umax与母线电压幅值Udc之比：

因此，以大中小正六边形为基本电压矢量调制时的最大调制系数ηmax分别为。

2 改进SVPWM算法

2.1 零序电压分析

共母线OW-PMSM 驱动系统存在零序回路，会导致相电流中含有零序电流［18］。系统中零序电压u0的值为：

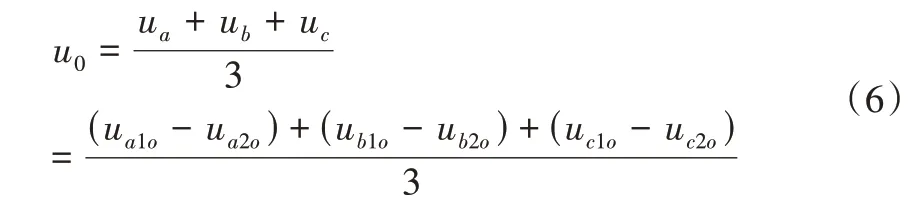
其中，ux（x=a，b，c）为OW-PMSM 的三相电压；ux1o（x=a，b，c）和ux2o（x=a，b，c）分别代表逆变器INV1 和INV2 的输出电压。因此，由双逆变器系统开关状态的不同，可以计算出零序电压的值，开关状态为43’（100011）时：

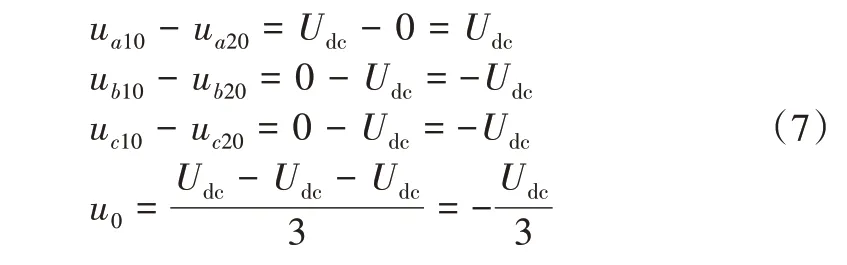
同理，可以计算出其他开关状态对应的零序电压值，如表1所示。

Table 1 Zero sequence voltage of dual inverter each switch state表1 双逆变器各开关状态对应的零序电压

观察表1 可知，当双逆变器的开关状态为88’、77’、11’、12’等时，共母线OW-PMSM 系统的零序电压值为零，在图3 空间中的对应位置是六边形HJLNQS 和位于原点的零电压矢量。因此，将此中六边形HJLNQS 作为SVPWM中的基本空间矢量，调制后驱动OW-PMSM 可实现双逆变器系统输出的零序电压为零。但是此方案最大调制系数ηmax仅为1，直流母线电压的利用率低，不利于高压大功率的应用场合。

2.2 大矢量SVPWM改进

为了提高共母线OW-PMSM 双逆变器系统输出的合成电压，本文将选择由最大电压空间矢量组成的大六边形GIKMPR 进行调制，如图4 所示。此时，双逆变器系统输出的最大调制系数ηmax可达。

Fig.4 Voltage space vector of large vector SVPWM图4 大矢量SVPWM电压空间矢量

其中，us为同步旋转的参考电压空间矢量，其需要在一个控制周期内由基本电压矢量合成得到。参与调制的非零基本电压矢量为UG（43’）、UI（61’）、UK（25’）、UM（34’）、UP（16’）和UR（52’），将调制空间分成了6个扇区。

对于零电压矢量的选择，传统的SVPWM 选择77’与88’参与调制，但在大矢量SVPWM 中会造成逆变器某一桥臂在单个周期内开关3 次增加开关损耗，如图5（a）所示。本文将选择78’和87’参与调制过程，可以看出图5（b）中各桥臂仅开关一次，且电机各绕组首尾连接INV1 和INV2的桥臂对称导通，说明此方法也适用于三相独立H 桥驱动。

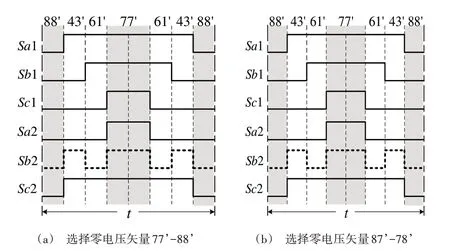
Fig.5 Dual inverter switching sequence in sector Ⅰ图5 扇区Ⅰ双逆变器开关顺序

2.3 零序电流抑制

对照表1 可以看出，选择的零电压矢量对应的零序电压并不为零。因此，可以通过重新分配零电压矢量87’和78’的作用时间，使得零序电压在单位开关周期内的平均值为零，类似于矢量调制中的伏秒平衡原则［15］。

以扇区Ⅰ为例，非零矢量43’和61’的零序电压值为-Udc/3 和Udc/3，零矢量87’和78’的零序电压值为-Udc和Udc。此时，单位开关周期t内零序电压伏秒平衡公式为：

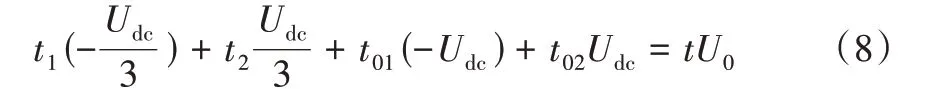
其中，t1和t2分别表示非零矢量43’和61’的作用时间；t01和t02分别表示零矢量87’和78’的作用时间；U0为此单位周期的平均零序电压。同时，引入零矢量分配系数k，令：

其中，t0为零矢量作用时间之和，且t0=t-（t1+t2）。若要使得U0的值为0，等式（8）的左端值应控制为0，结合式（9）进一步求得分配系数k为：

同时，当图4 中参考电压电角度θ=0 时，非零矢量仅有43’参与调制，此时对应的零序电压为-Udc/3。根据上文的抵消方案，应采用零矢量78’参与调制，可以求出抵消方案的极限情况，令分配系数k为0，则由等式（8）有：

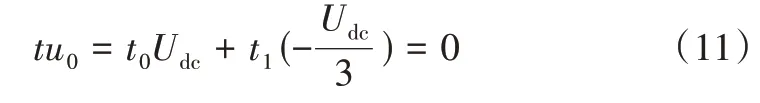
结合调制中的矢量合成伏秒平衡原则，此时：

将式（12）代入式（11）后，求得参考电压矢量us=Udc。因此，当参考电压矢量幅值不超过Udc时，理论上可以实现开关周期内平均零序电压控制到0，且Udc也是中矢量SVPWM 的线性调制区。因此，本文调制算法除拓展共母线OW-PMSM 系统的直流母线电压利用率外，还可以实现类似中矢量SVPWM 算法的零序电流抑制效果。

2.4 算法实现过程

2.4.1 扇区判断

OW-PMSM 驱动系统中改进大矢量SVPWM 扇区判断过程类似于传统单逆变器系统的SVPWM，采用参考电压矢量us位于两相静止坐标系αβ中的uα和uβ参与扇区判断［19］，令：

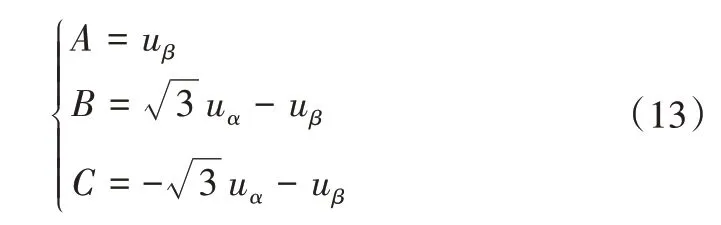
接着定义变量P1、P2、P3、P：若A>0，则P1=1，否则P1=0；若B>0，则P2=1，否则P2=0；若C>0，则P3=1，否则P3=0。由式子P=P1+2P2+4P3的值可直接判断参考电压所处的扇区，如表2所示。

Table 2 Correspondence between P and sector表2 P与扇区的对应关系

2.4.2 矢量作用时间与顺序

判断好参考矢量所处扇区后，需要计算该扇区内参与调制过程矢量的作用时间与作用顺序。根据矢量合成关系和单位开关周期内伏秒平衡原则可以求得各基本电压矢量的作用时间，令：

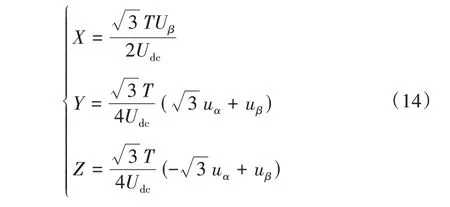
为了实现如图5 所示的七段式SVPWM 调制过程，使得单位开关周期内双逆变器各桥臂仅开关一次。定义t1和t2分别为单个开关周期内第一个和第二个基本电压矢量的作用时间，可以列出各扇区内各矢量的作用情况，如表3所示。

Table 3 Vector action sequence and time of each sector表3 各扇区相邻矢量作用顺序与作用时间

2.4.3 零矢量重分配

在确定各扇区矢量切换点之前，为了抑制OW-PMSM系统的零序电压，需对零矢量作重分配处理。观察表1 可知，基本电压矢量UG（43’）、UK（25’）和UP（16’）的零序电压为-Udc/3，它们的作用时间对应表3 中的t1；UI（61’）、UM（34’）和UR（52’）的零序电压为Udc/3，它们的作用时间对应表3 中的t2。因此，零矢量重分配过程中，各扇区矢量切换点的计算具有统一性，令：

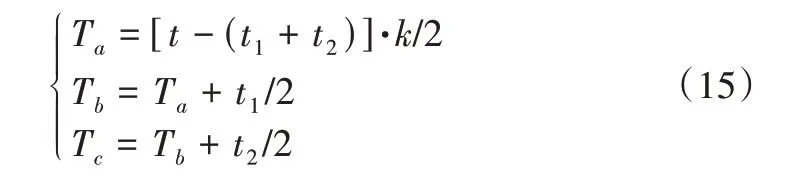
因此，各扇区内双逆变器系统矢量的切换时间点（即各开关管开关状态改变点）如表4所示。

最后，将输出的各扇区切换时间点与三角载波信号比较后生成PWM 波控制双逆变器系统，调制出相应的电压空间矢量驱动OW-PMSM。

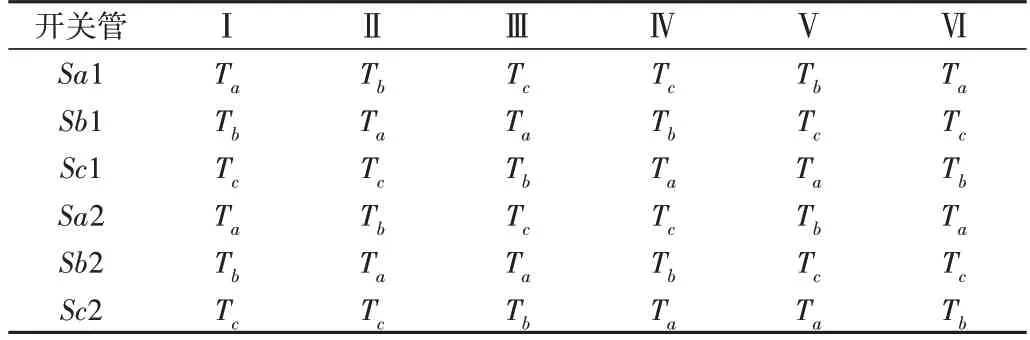
Table 4 Vector switching time point of each sector表4 各扇区矢量切换时间点

3 仿真实验

3.1 仿真实验设计

为验证本文所提改进SVPWM 算法，在Matlab/Simulink环境中搭建共母线OW-PMSM 驱动控制系统的仿真模型［20］，如图6 所示。整个控制系统由转速外环和电流内环采用PI 控制器构成，同时采用坐标变换后实现了OWPMSM 的dq轴解耦控制。仿真中OW-PMSM 驱动系统的主要参数如表5所示。

Fig.6 Block diagram of common bus OW-PMSM drive system图6 共母线OW-PMSM 驱动系统框图

Table 5 Main parameters of drive system表5 驱动系统主要参数

3.2 仿真结果与分析

首先验证低母线电压下运行情况。当母线电压设置为26V 时，分别采用中矢量和大矢量SVPWM 后，共母线OW-PMSM 驱动系统仿真结果如图7 所示（彩图扫OSID 码可见）。从图7（a）转速和转矩对比可以看出，虽然它们都能输出5N·m 电磁转矩，但中矢量SVPWM 驱动电机达不到给定转速600r/min，而大矢量SVPWM 能够正常驱动电机，说明其母线电压利用率更高。图7（b）为三相电流仿真波形，相电流都有一定畸变，且大矢量SVPWM谐波电流含量较高。

接着验证本文所提改进大矢量SVPWM 算法。将母线电压设置为50V，分别采用大矢量和改进大矢量SVPWM后，共母线OW-PMSM 驱动系统仿真结果如图8 所示。从图8（a）的三相电流仿真波形中可以看出，应用改进大矢量SVPWM 后，电流波形正弦度明显提高，且图8（b）中的零序电流从4A 降低到1A 以下。进一步利用Simulink 中的powergui 模块对电流FFT 谐波分析得到图8（c），可以看出电流的THD 值由56.2%下降到9.4%，且3 次谐波含量由55.5%降低到4.03%，说明本文所提改进SVPWM 算法的有效性。

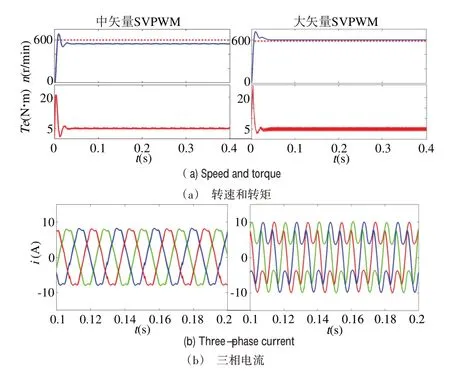
Fig.7 Simulation comparison of different SVPWM图7 不同矢量SVPWM仿真对比（彩图扫OSID码可见）

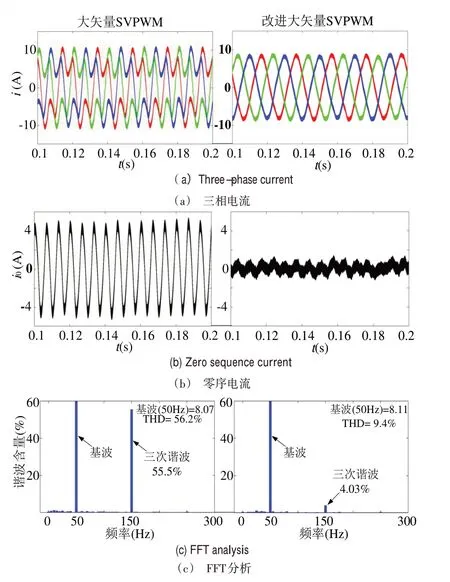
Fig.8 Simulation comparison of improved SVPWM图8 改进SVPWM仿真对比

4 结语

本文针对共母线OW-PMSM 驱动系统，提出了一种改进的SVPWM 算法，并基于MATLAB/Simulink 平台搭建了电机系统仿真模型。该算法拓宽了双逆变器系统的线性调制区，增大了母线电压利用率，并使得单位开关周期内平均共模电压为零，抑制了电机中的零序电流，直接降低了相电流3 次谐波的含量。但是实际应用中，共母线OWPMSM 还可能存在由谐波反电动势引起的零序电流，因此对本文所提算法还需作进一步研究。