基于主成分分析与K-means聚类的汽车行驶工况构建

2022-05-26段宇帅

软件导刊 2022年5期

段宇帅

（浙江理工大学信息学院，浙江杭州 310018）

0 引言

汽车行驶工况［1］（Driving Cycle）又称车辆测试循环，是描述汽车行驶速度—时间曲线，体现汽车道路行驶的运动学特征，是汽车行业的一项重要的共性核心技术，是车辆能耗测试方法和限值标准的基础，也是汽车整车和零部件参数的主要基准。目前，发达国家的汽车技术采用NEDC（New European Driving Cycle）工况［2］，如图1 所示。近年来，我国的道路交通状况、人口密度和城镇化发生了很大变化，以NEDC 工况为基准所优化标定的汽车已不能满足需求，急需基于我国国情构建新的城市汽车行驶工况，许多地方构建了符合自己城市实际的汽车行驶工况。

1 相关工作

汽车行驶工况曲线作为评价汽车的标准，在评价燃油经济［3］和车辆设计［4］等方面得到广泛研究，如基于马尔可夫链和K-means 聚类构建工况曲线［5］；采用改进的马尔科夫蒙特卡罗方法构建北京市的行驶工况图［6］；采用主成分分析和聚类方法构建行驶工况［7-11］等；文献［12］从怠速、加速、减速、匀速阶段来判断工况曲线的合理性，有一定局限性；文献［13］利用主成分分析和FCM 聚类构建了合肥市的行驶工况本文使用15种特征参数进行更全面的描述。

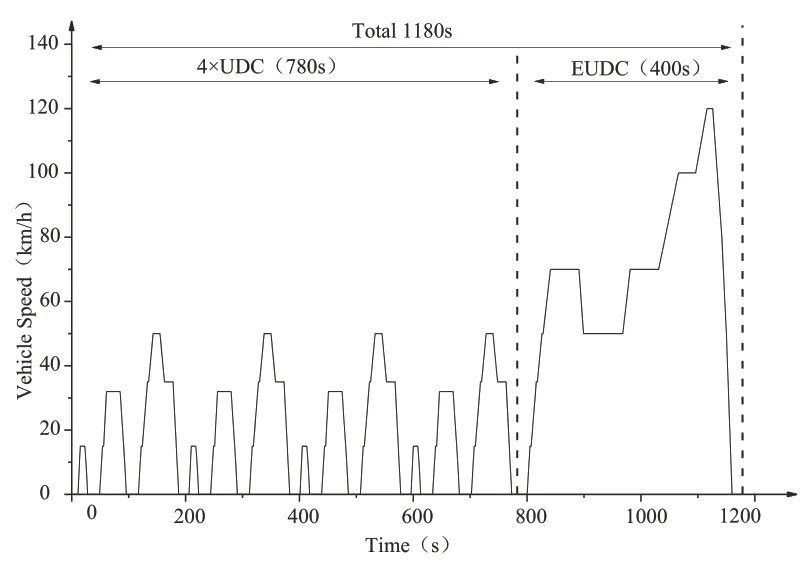
Fig.1 European NEDC operating conditions图1 欧洲NEDC工况

在前述研究基础上，本文根据某城市轻型汽车实际道路行驶采集的数据（采样频率1Hz），基于主成分分析和Kmeans 聚类方法构建汽车行驶工况曲线。首先对原数据集进行不良数据的剔除，然后根据运动学片段定义，利用平均加速度、怠速时间比、速度标准差等参数提取运动学片段特征。利用主成分分析方法对特征参数矩阵进行处理，得到3个主成分；之后用K-means 聚类对运行学片段聚类，获得3 类代表不同速度的片段，最终构成汽车行驶工况曲线。为了验证本文的汽车行驶工况曲线，使用相对误差和绝对误差分析总样本和本文工况曲线，得到的结果误差越小，证明曲线越合理。

2 数据预处理

2.1 运动学片段定义

运动学片段［14］指汽车从怠速状态初始阶段到下一个怠速状态初始阶段之间的行车速度区间，如图2 所示。从图中可以看出一段运动学片段包含怠速、加速、匀速和减速阶段，这些阶段包含汽车的各种行驶信息。

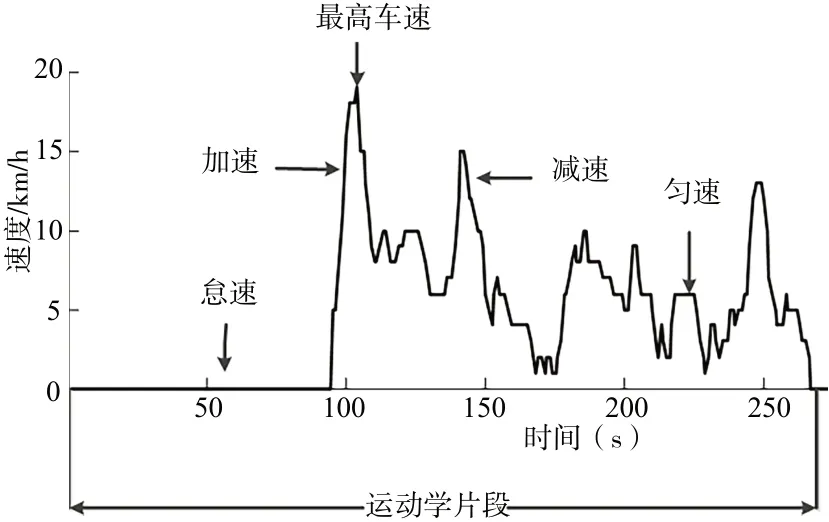
Fig.2 Kinematic segment definition图2 运动学片段定义

2.2 不良数据处理

由于数据是采集设备直接记录汽车行驶的原始数据，所以会包含一些不良数据，如数据中的时间不连续、汽车加、减速度异常、汽车长时间速度为零或低速状态、怠速时间过长等。

根据不良数据问题设计了剔除算法，如图3所示。

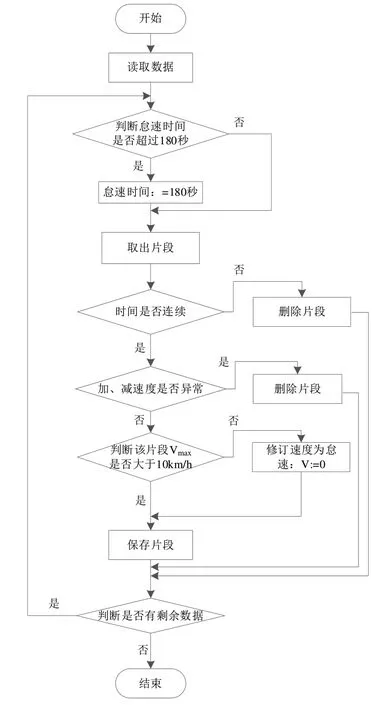
Fig.3 Flow of culling algorithm图3 剔除算法流程

算法步骤如下：

输入数据；

处理怠速时间过长数据段；

处理不连续的数据；

处理加、减速度异常的数据；

输出数据。

2.3 运动片段提取

对采集的3 个数据集进行运动片段提取，应用贪婪算法［15］直接筛选数据，进而获取运动学片段，见表2。

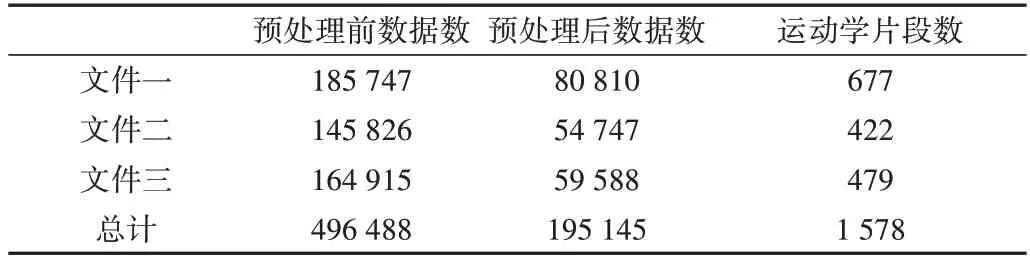
Table 2 Kinematic segment data表2 运动片段数据

该算法求解步骤如下：

输入数据，分批处理数据；

选取第一个速度零点；

判断数据段是否符合运动学片段条件；

获取运动学片段，选取下一个速度零点继续搜寻；

输出运动学片段。

3 汽车工况图构建

3.1 运动学片段特征提取

汽车的行驶过程可以看作大量运动学片段的组合，对汽车运动数据作预处理、获取片段后，通过分析运动学片段的运动特征可得出车辆的运动特征。对运动学片段主要从运行距离、最大速度、平均加减速度、加速度标准差等几方面进行特征分析，本文选用如表3 所示的15 个特征参数描述运动学片段。处理汽车运动数据1 578 个运动学片段的15个参数值，如表4所示。

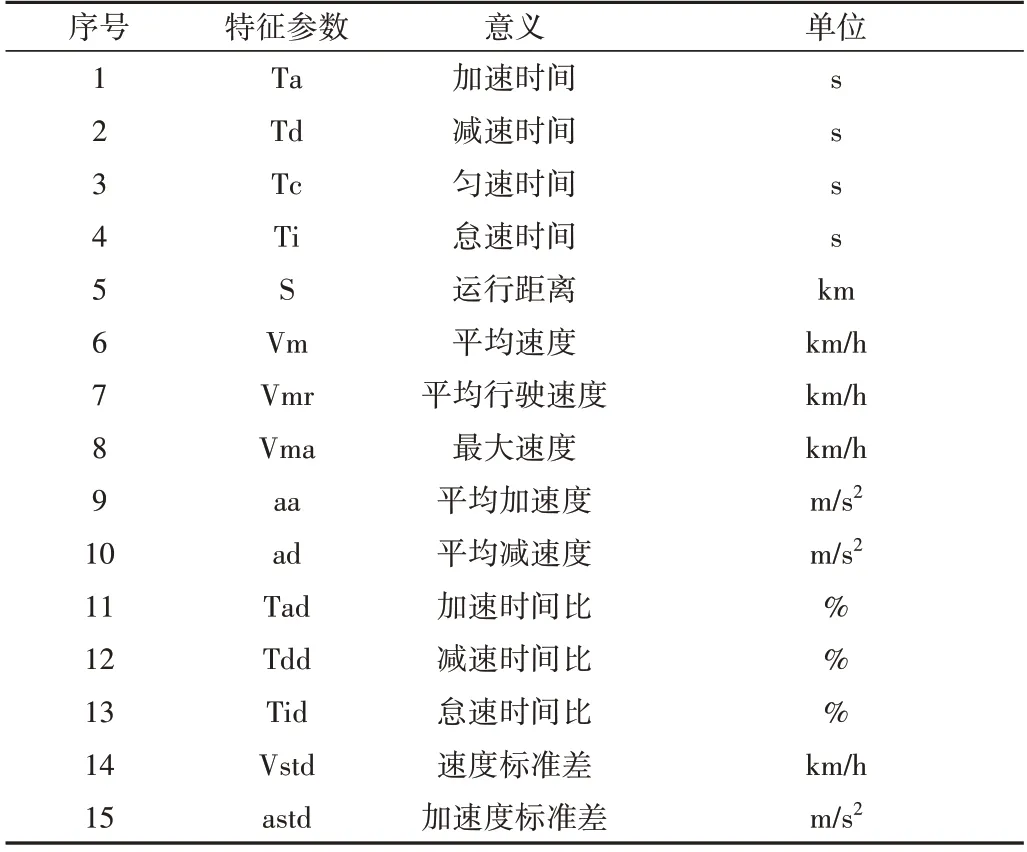
Table 3 15 feature parameter definitions表3 15个特征参数定义

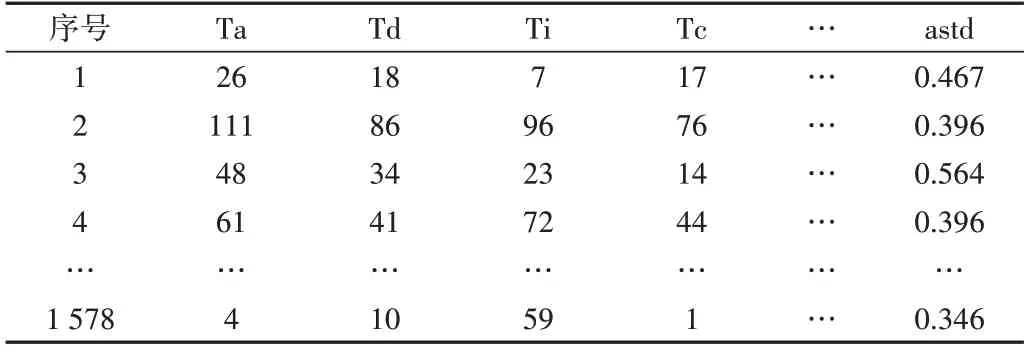
Table 4 Kinematics fragment eigenvalue matrix表4 运动学片段特征值矩阵

3.2 主成分分析

对1 578 个运动学片段的特征参数进行主成分分析。设n为运动学片段数量，p为特征参数数量，则相应的矩阵为：

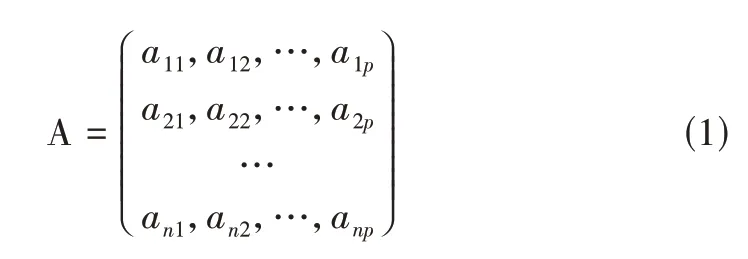
称A矩阵为原始数据矩阵。对原始矩阵进行标准化，消除指标间的差异性。

计算得到λ1，λ2，…，λp共计p个特征值，且λ1>λ2>… >λp>0，并可得到与之相对应的特征向量u1，u2，…，up，将所有特征向量构建成一个特征矩阵U：

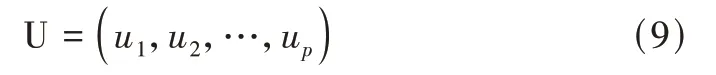
每个主成分的贡献率计算如下：

一般研究认为主成分的累计贡献率超过80%时，这部分主成分就包含了代表原指标的绝大多数信息。本研究认为当贡献率大于85%时即可代表原指标。

由表5 可知，前3 个主成分的累积贡献率之和已经达到84.57%，并且这3 个主成分的特征值都大于1，因此，用前3 个主成分就能反映出15 个特征参数的大部分信息。同时由图4（彩图扫OSID 码可见，下同）可以很明显看出各个主成分特征值的整体变化趋势，结合累计贡献率可以看出应当选择前3 个主成分。经过主成分分析得到一个主成分载荷矩阵。某个参数在某个主成分上的载荷系数绝对值越大，越说明该参数与这个主成分的相关系数越大，越能反映主成分的信息量。载荷矩阵如表6 所示。第一主成分M1 主要反映加速时间、减速时间、路程、平均速度、最大速度、速度标准差、加速时间比；第二主成分M2 主要反映怠速时间比、加速度标准差、减速时间比；第3 主成分M3 主要反映匀速时间比、平均行驶速度、平均加速度、平均减速度。

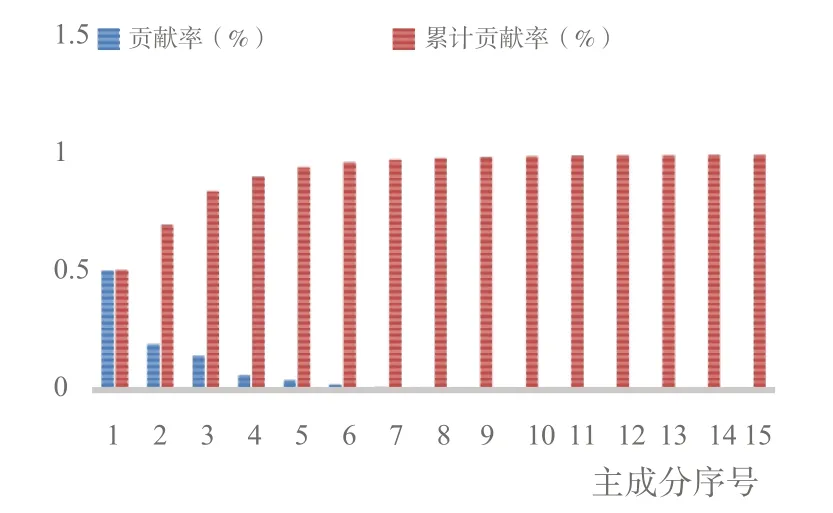
Fig.4 Histogram of the contribution rate of principal components图4 主成分贡献率柱状图

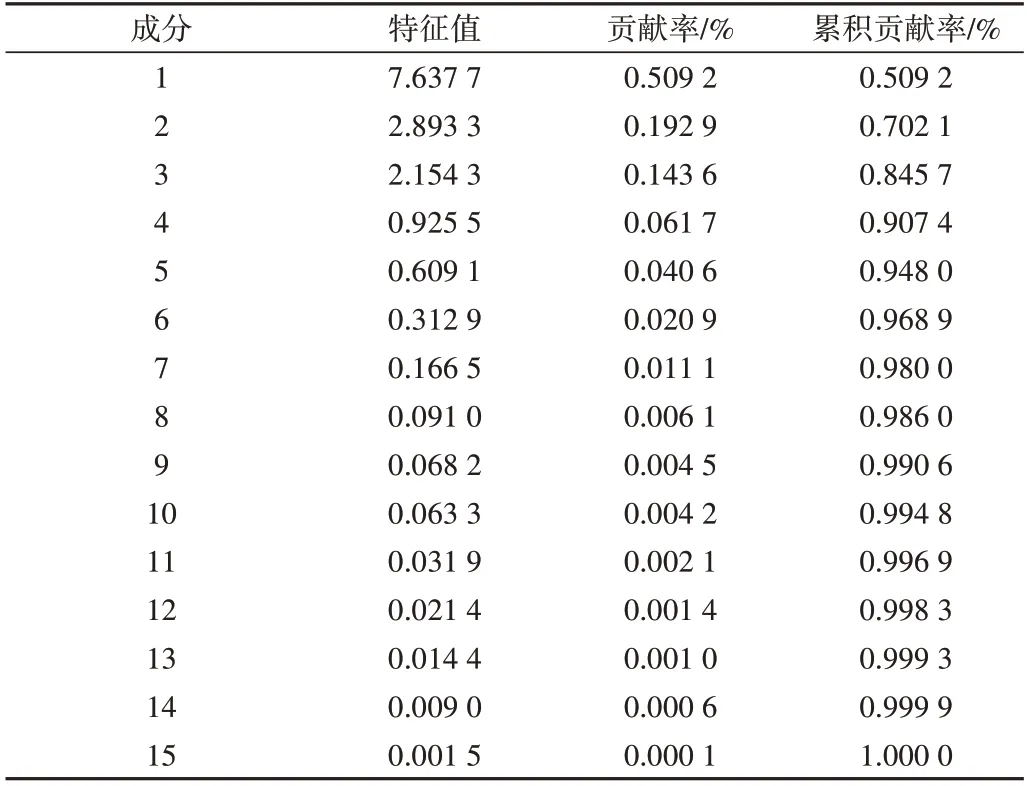
Table 5 Principal component contribution rate表5 主成分贡献率

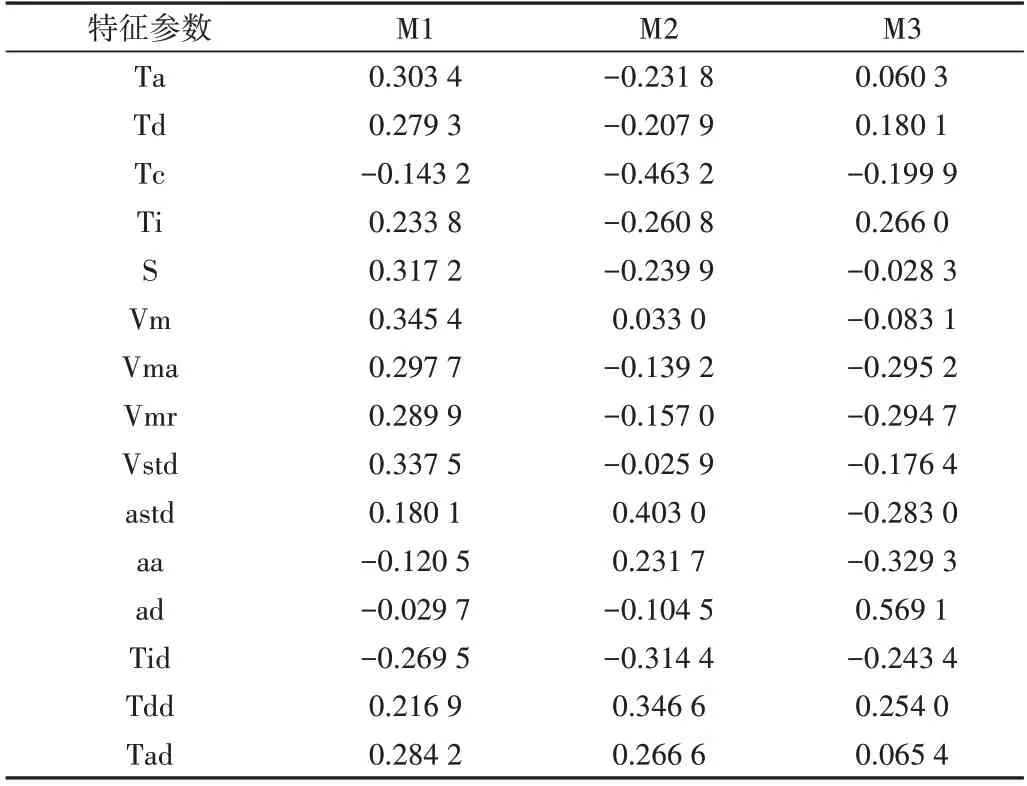
Table 6 Component load matrix表6 主成分载荷矩阵

3.3 K-means聚类分析

利用K-means 方法［17-18］对由主成分分析得到的3 个主成分得分矩阵进行聚类。将运动学片段分为3 类，如图5所示，分别计算各类别的平均特征值，结果见表7。

第一类运动学片段的平均速度和平均最大速度最低，怠速时间占总运行时间比例处于中间位置，第一类为中速片段；第二类运动学片段的平均速度和平均最大速度最高，怠速时间占总运行时间比例最低，第二类为高速片段；第三类运动学片段的平均速度和平均最大速度处于中间位置，怠速时间占总运行时间比例最高，第三类为低速片段。

Fig.5 Kinematic fragment cluster图5 运动学片段聚类

Table 7 Average eigenvalue of each class表7 各类别的平均特征值

3.4 汽车驾驶工况构建

在每个聚类中选取与该类特征值相关系数最大的代表性运动学片段构建车辆的行驶工况。采用随机选择法［19］、最佳增量法［20］选取运动学片段，一般工况时长约为1 200～1 300s，可通过各个类别时间在总体数据中所占的比例来确定最终拟合工况中所选取的片段数量。确定各类片段所需要的数量通过式（11）计算：

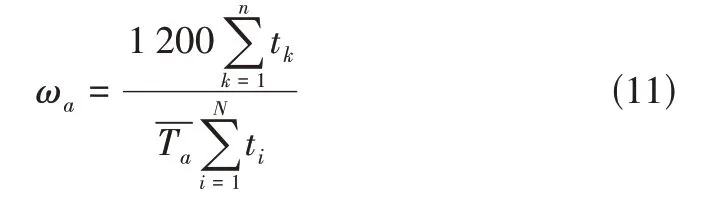
其中，ωa代表第a类片段所需要的数量；n表示第a类片段中所含运动学片段的数量；tk表示第a类片段中第k条片段的长度；表示第a类片段的平均长度；N 表示总体中所有运动学片段的个数；ti表示总体中第i个运动学片段的长度。

利用式（11）分别在各个类别中选取片段，构建一条汽车行驶工况图，如图6所示。

Fig.6 Car driving cycle图6 汽车行驶工况

4 汽车行驶工况评价

在研究中一般利用相对误差和绝对误差来反映数据之间的差异，汽车行驶工况与采样总体的15 个特征值的差距不大，多数特征值都比较相近。观察表7 发现，各参数值间的相对误差较小。本文构建的工况图和原始数据差异较小，可以很好地反映汽车的行驶状态，即构建的汽车行驶工况图是合理的，如图7所示。

Table 7 Driving cycle diagram error analysis表7 工况图误差分析

5 结语

为了更好地构建汽车行驶工况曲线，本文提出一种基于K-means 聚类的汽车行驶工况构建。使用15 个特征参数进行特征提取，采用主成分分析法进行降维，利用Kmeans 聚类方法进行分类，最终从各类别分别提取运动学片段组成一条汽车行驶工况曲线。实验证明本文使用的剔除算法有效剔除了不良数据，适用于大数据处理。运动学片段的获取方法合理有效，精确性较高。本文不足之处是某些特征参数的绝对误差较大，可在未来工作中缩减误差。本文可为后续计算各个城市的汽车行驶工况曲线研究提供参考。