国内五省市及地区抗疫水平多准则决策方法排序比较分析

刘阿龙，屈绍建

（1.上海理工大学管理学院，上海 200093；2.南京信息工程大学管理工程学院，江苏南京 210044）

0 引言

2019 年底以来，COVID-19 新冠肺炎对全球经济发展和社会稳定造成了严重影响，成为至20 世纪初“西班牙流感”大流行之后最为重大的疫情事件［1］。截至2021 年4月，全国有10 万余人感染COVID-19 新冠肺炎，死亡人数约4 800人，疫情形势十分严峻［2-3］。

为了限制疫情蔓延，武汉市有近1 100 万人被封锁，紧接着封锁范围逐步扩大到湖北省其它城市［4］。上海市政府建立了应对新冠肺炎联防联控工作小组，要求医疗卫生部门、口岸检验检疫部门和机场管理部门对所有国际航班实施远机位停靠和登机检疫。中国台湾于2019 年12 月31日开始筛查所有从武汉直飞的航班，并建立了新冠检测方案［5］。但由于各省市地区疫情严重程度、经济发展、地理位置等差异，导致各地区采取的措施各不相同，因此评价各地区抗议水平的标准难以统一。为此，本文参考经济、应急救援、疫苗研发、社会因素和传播控制5 个标准，建立多准则决策（Multi-Criteria Decision Making，MCDM）模型对中国部分省份的抗疫水平进行排序，并解决了以下3 个问题：①应该用什么标准评价中国各省份的抗疫水平；②哪些省份抗疫水平较高；③当标准权重变化时，排序将如何变化。

由于武汉是应对疫情最迅速的城市；上海和北京作为我国的经济和政治中心，市政府迅速建立应急联防联控机制，起到良好的带头作用；香港和台湾在疫情蔓延时，疫情防控反应及时。因此，本文将武汉、上海、北京、香港、台湾5个省市及地区作为研究对象。

1 研究现状

1.1 多准则决策方法

MCDM 是运筹学领域中广泛用于处理决策标准问题的一种常用方法［6-8］，几乎所有MCDM 模型都是基于决策问题行为而被所提出［9-10］。总而言之，MCDM 是一种同时基于一组不同标准进行定量和定性分析的比较方法［11］，效率较高，能够提高决策质量，旨在帮助决策者选择最佳选项，因此被决策者广泛使用［12］。并且，该方法能够对可行选项进行分类，对其性能进行降序排列［13-14］。

MCDM 方法包括加权求和法（Weighted Summation Method，WSM）、加权乘积法（Weighted Product Method，WPM）、层次分析法（Analytic Hierarchy Process，AHP）、模糊层次分析法、逼近理想解排序法（Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS）、多准则妥协解排序法（VIKOR）和多目标规划。每种方法都有其优缺点和应用领域，利用多种方法解决同一多准则决策问题，可提供更稳健的决策信息［15］。

2.2 实际应用

如今，多准则决策已被广泛应用于新冠肺炎疫情、医疗卫生等领域。例如，新冠疫情的防备政策、医院备灾情况、卫生政策反应等。Requia 等［16］提出一种空间多标准方法，以城市为单位评估巴西医疗保健系统因疫情造成超出医疗保健能力风险的概率。通过结合多准则决策方法和空间分析估算超出风险的概率，为政府机构提供行动选择，为国家、地区和地方制定有效的卫生公共政策提供支持。Albahri 等［17］开发了一种结合VIKOR 和层次分析法的方法，制定和评估新冠肺炎医学图像分类中使用的人工智能技术基准，并讨论未来该技术的研究方向。随后，Albahri 等［18］基于生物学需要，提出将机器学习和MCDM 相结合的方法。

由于各种MCDM 方法考虑的方面和标准各不相同，使用不同方法评定同一国家省市内的抗疫水平，结果也不尽相同。目前，MCDM 方法大多用于研究新冠肺炎疫情期间医疗卫生系统、病毒检测、风险监控等，但评价各国家地区抗疫水平的研究较少。为此，本文具有以下3 个方面贡献：①确定中国各省市抗疫的评定标准；②利用MCDM 方法对中国各省市抗疫水平进行研究，为各国家地区提出有效的抗疫建议；③从经济、应急救援、疫苗研发、社会因素和传播控制方面进行敏感性分析。

2 评定标准

本文将中国各省市及地区的抗疫水平研究评价标准分为5 大类：经济、应急救援、疫苗研发、社会因素和传播控制。其中，经济维度指与成本相关的标准，例如应急物资成本、运营成本和设施建设成本等；应急救援维度指组织管理、快速反应、救援技术和救援保障；疫苗研发维度指疫苗研究技术的成熟度、科研人员投入度及其研究效率；社会影响维度指人们对疫情的恐慌程度、疫情对社会就业的影响及国家对人们生活的保障程度；传播控制维度指国家对省市区县的封闭控制等。具体评定标准见表1。

Table 1 Evaluation criteria表1 评定标准

续表

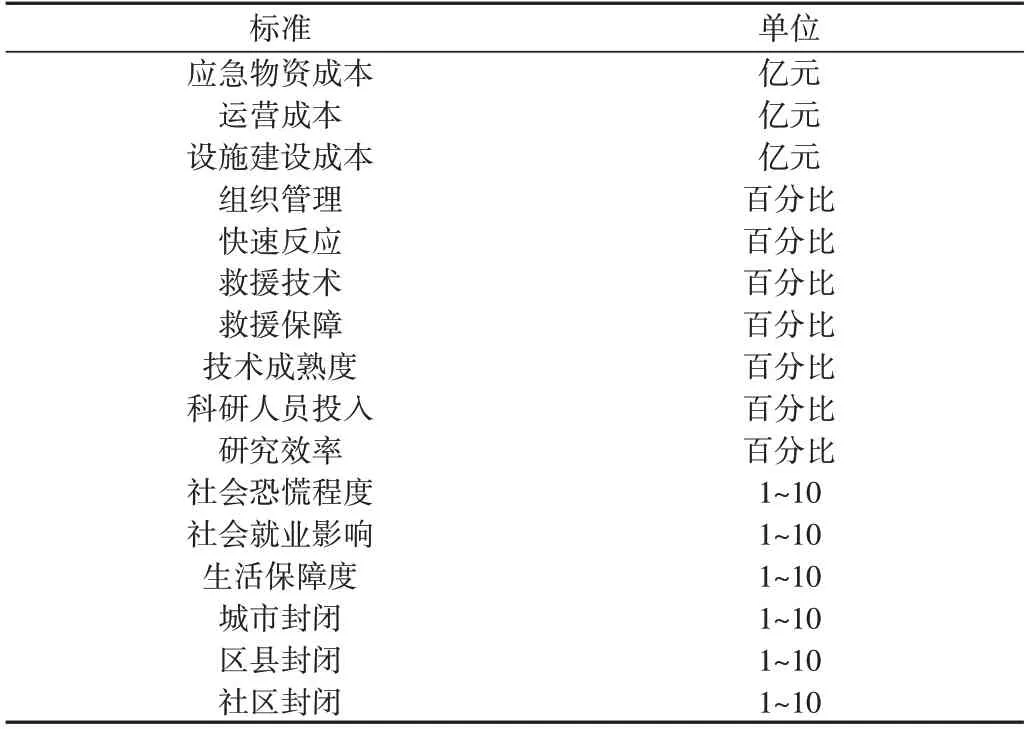
Table 2 Research data of epidemic resistance level表2 抗疫水平研究数据

由表2 可见，组织管理、快速反应、救援技术、救援保障、技术成熟度、科研人员投入和研究效率均使用百分比进行评估，越高则表示越好。社会恐慌度、就业影响、生活保障度、城市封闭、区县封闭和社区封闭均使用1～10 的定性量表进行评估。本文研究数据来源于数据处理后的2019 年12 月至2020 年12 月在线社交渠道收集的200 余份调查问卷。具体数据如表3所示。

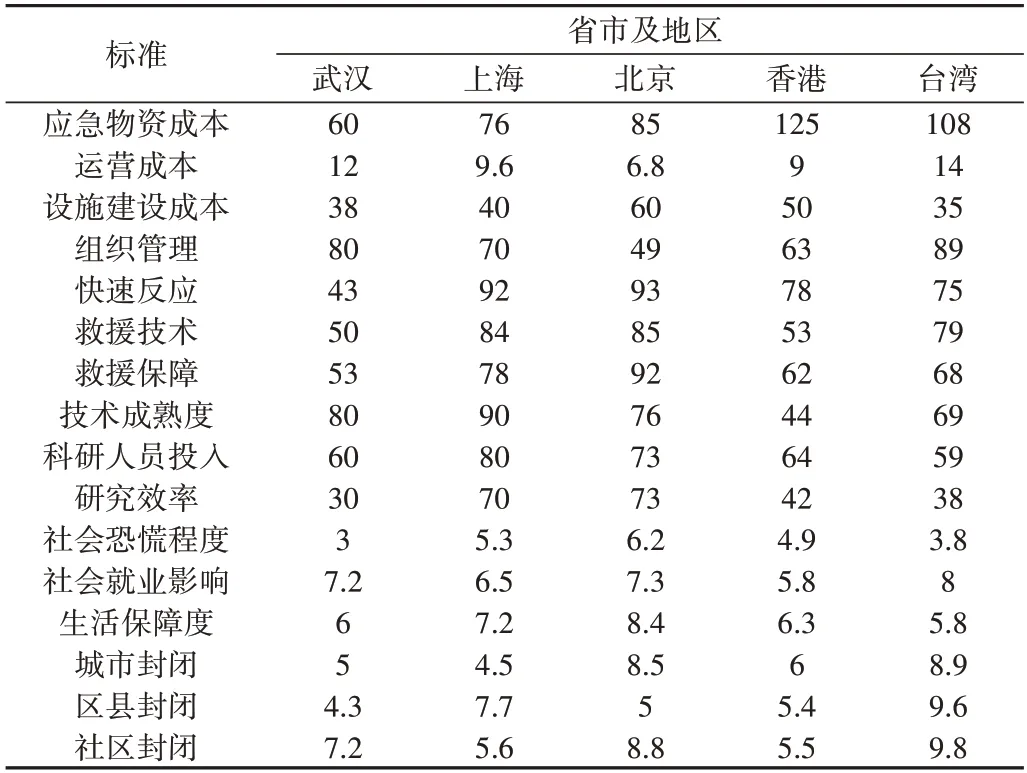
Table 3 Preliminary data of epidemic resistance level表3 抗疫水平初步数据

3 MCDM

在确定评价标准和备选方案后，本文结合熵和MCDM方法对中国各省市及地区抗疫水平进行排序。为了确定每个准则的重要性，首先使用香农熵计算每个准则的权重。然后，利用4 种MCDM 方法对各省市抗疫水平进行排序，并为各国家地区提出一些有效的抗疫建议。

3.1 标准权重计算

权重可分为主观权重和客观权重。主观权重主要基于经验和主观判断的专家意见确定，例如层次分析法和德尔菲法；客观权重则直接从备选方案的真实数据中提取，例如熵权方法，该方法减少了决策者的主观影响，在一定程度上增加了客观性。

熵最早来原于物理学，用来表示任何一种能量在空间中分布的均匀程度，能量分布得越均匀，熵就越大，可用于计算系统的无序度。Shannon［19］将熵应用于解决信息问题，使其成为处理不确定性的方法，根据熵理论，熵值越小，提供的信息就越多，则应赋予更大的权重［20］。Le 等［21］提出了一种基于混合多目标分解模型的机床选择方法，该方法综合赋权模糊决策试验室（FDEMATEL）获得的主观权重与熵权（EW）获得的客观权重，提出去模糊VIKOR（LDVIKOR）算法对可选方案进行排序。通过实例验证，该方法选择的最佳和最差机床与实际排序一致性较高。Rogulj 等［22］提出一种基于粗糙中性集理论算法，以解决历史人行天桥修复的战略规划问题，利用新型交叉熵与加权粗糙中性对称交叉熵求得效用测度、后悔测度和VIKOR指数值。通过实例验证，该模型在处理复杂多准则决策过程时的鲁棒性、可行性和有效性均较高。Arian 等［23］通过结合熵、主观权重及全乘比例分析多目标优化处理工程设计和生产过程中材料的选择问题。

3.2 香农熵权计算

假设一个决策问题有m个备选方案（A1，A2，…，Am）和n个标准（C1，C2，…，Cn），初始决策矩阵为［24］。

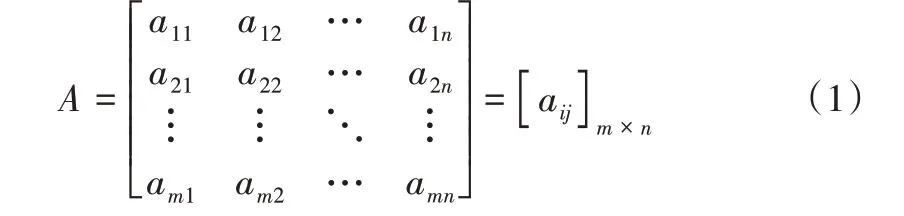
式中，元素aij为第i个备选方案的第j个标准。

步骤1：标准化决策矩阵。

步骤2：计算熵（Compute Entropy）。

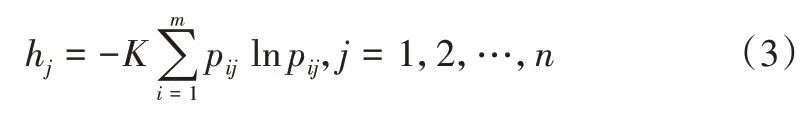
式中，K=1/lnm。

步骤3：计算每个标准的权重。

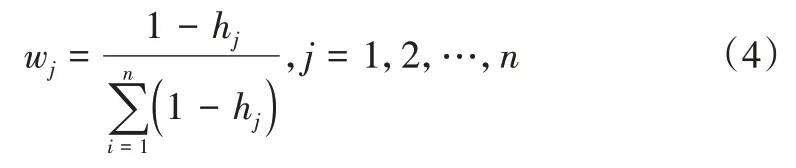
3.3 加权求和法

WSM 是最简单和广泛使用的MCDM 方法。一般情况下，WSM 将成本标准转化为效益标准，通过将每个标准值除以所有标准的总和构建归一化矩阵［16］。然后，将每个备选方案的总得分乘以矩阵的权重，最高分即为最优选择。

3.4 TOPSIS

TOPSIS 是一种常用的综合评价方法，该方法能充分利用原始数据信息精确反映各评价方案之间的差距，并且能根据正负理想解间的距离对备选方案进行排序［25］。

3.5 VIKOR

VIKOR 能够解决具有冲突和不可测量标准的决策问题。在VIKOR 模型中，通过比较接近理想解的度量方式进行折衷排序。具体步骤如下：

步骤1：计算归一化决策矩阵。

式中，I1，I2为收益和成本标准集合。

步骤3：计算Si和Ri。

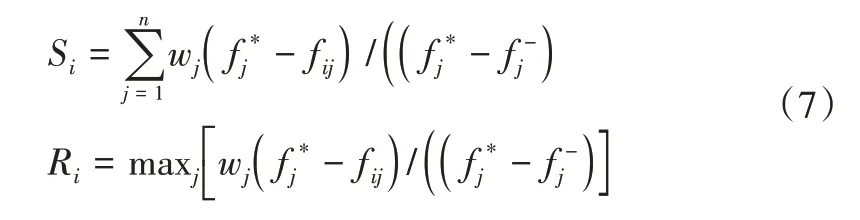
式中，wj为标准权重。

步骤4：计算Qi。

其中，S*=minSi、S-=maxSi、R*=minRi、R-=maxRi、v被定义为最大群体策略的权重，(1 -v)为个体后悔权重，通常设置为0.5。

步骤5：对备选方案按照Qi值进行降序排列。

3.6 ELECTRE

ELECTRE 方法的核心是风险间的级别高于关系，从一系列风险中筛选出相对级别较高的风险。

步骤1：构造规范化决策矩阵：

步骤2：构造加权归一化决策矩阵V。

步骤3：确定一致性和非一致性集合。

若第k列中第i行的v值相较于第j行的v值更高，则k归类于一致性集合Cij，否则属于非一致性集合Dij，其中k=1，2，…，m。

步骤4：将各元素不一致性集合的标准权重相加，得到一致性矩阵。

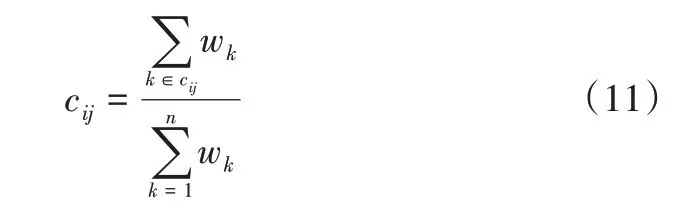
步骤5：计算不一致矩阵并修正。

式中，S为所有标准的集合。

步骤6：计算修订后的总矩阵Y。

步骤7：计算净优势值。

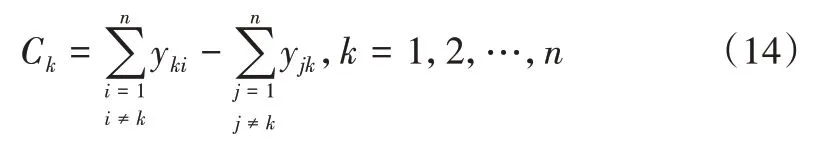
步骤8：按照Ck的值递增顺序对备选方案进行排序。

3.7 方法总结

MCDM 可帮助决策者根据各种标准评估所有替代方案，以获得更合适的解决方案。然而，每种方法都有其自身的优缺点，通常难以确定某一种方法相较于其它方法更可取，主要取决于分析师的主观偏好。本文中4 种MCDM方法存在一定的共同点：①对每个标准赋值；②均乘以相应权重；③通过总分进行排名。由表4 可见，VIKOR 和TOPSIS 基于代表参考点接近度的聚合函数，这两种方法均使用不同种类的归一化消除准则函数单元。其中，VIKOR使用线性归一化，TOPSIS 方法则使用矢量归一化。

Table 4 Comparison of four MCDM methods表4 4种MCDM方法比较分析

4 实验结果

由表5 可见，传播控制是评价各省市及地区抗疫水平最重要的因素，其次是应急救援水平、疫苗研发和经济因素，排名最后的是社会影响。在所有标准中，排名第1 的是疫苗研究效率，其次是区县封闭及城市封闭、应急物资的成本和救援的快速反应，社会恐慌度、运营成本和社区封闭的排名相对靠前，剩下的标准排名相对靠后。

对WSM、TOPSIS、VIKOR、ELECTRE 进行数据测试，测试结果见表6。其中，TOPSIS、VIKOR 和ELECTRE 都将武汉排至第1 名、上海排至第2 名、北京排至第3 名；4 种方法均将香港和台湾排至最后两名。

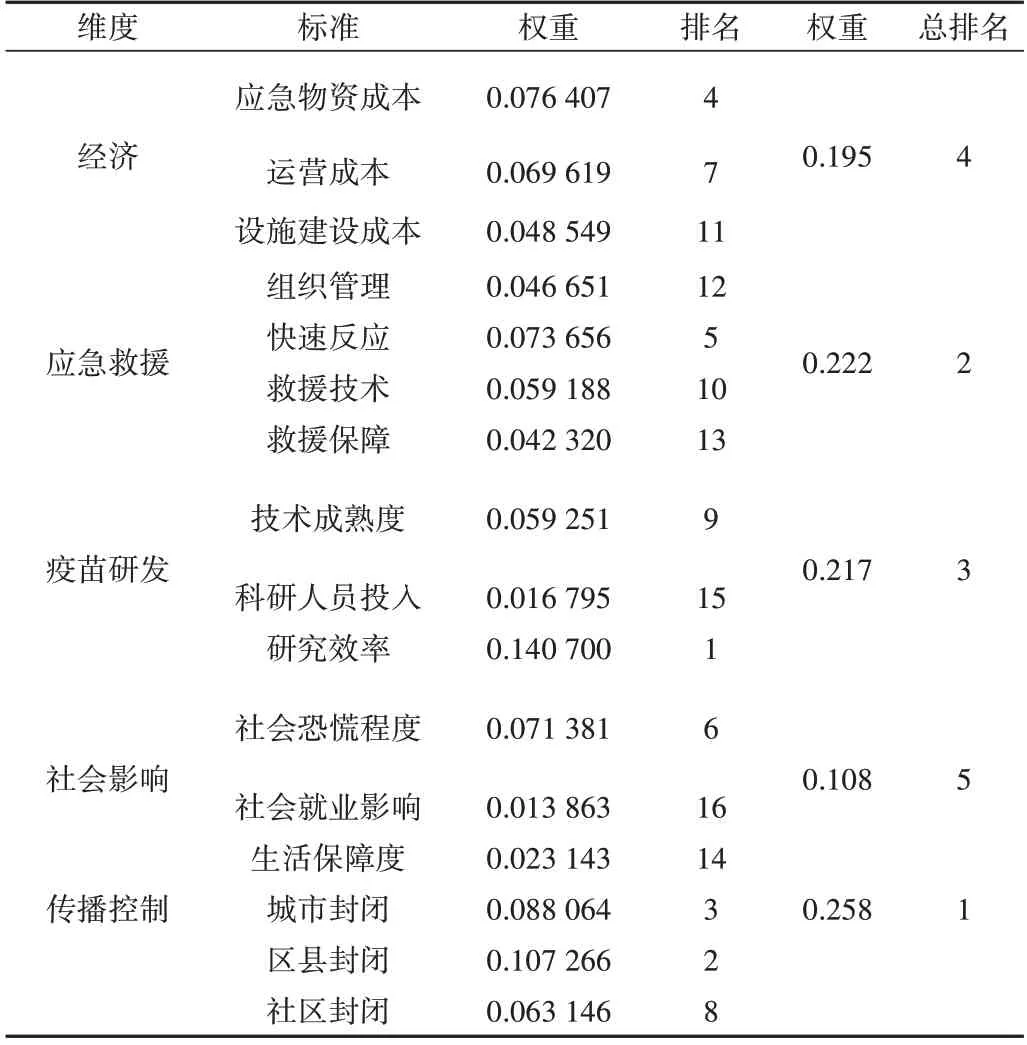
Table 5 Weight ranking表5 权重排名

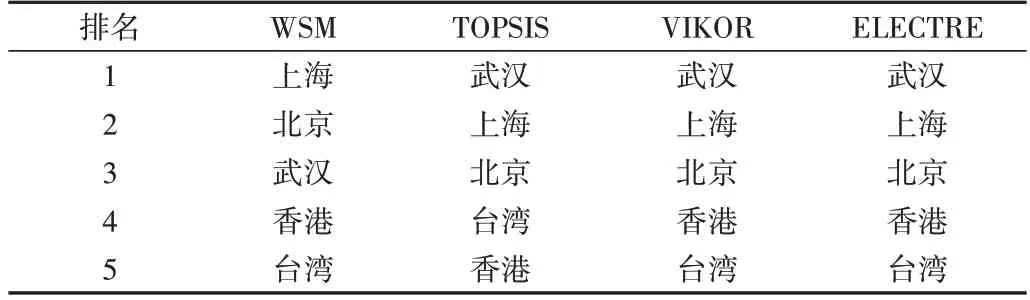
Table 6 Final ranking result表6 最终排名结果

5 敏感性分析

由于标准权重显著影响排名，因此本文利用敏感性分析各省市抗疫水平的排名如何因标准权重变化。首先，通过增加或减少5%或50%的标准权重调整权重值。图1 为每个单独标准的灵敏度分析结果（彩图扫OSID 可见，下同）。

为了将总标准权重固定为1，在每个标准权重增加时，同步将其余标准权重应该按比例进行减少。如图1 所示，深绿色条表示在调整标准权重之后，标准排名并未变化，浅绿色条表示排名存在轻微变化。杆长表示标准重量的容许程度，杆长较长代表标准重量的敏感度较低。

由图1 可见，C6（救援技术）和C9（科研人员投入）的敏感性最低，当使用4 种MCDM 方法改变权重时，排名不变；C1（应急物资成本）、C8（技术成熟度）、C12（就业影响）、C13（生活保障度）较为稳定；C2（运营成本）和C15（区县封闭）最为敏感。

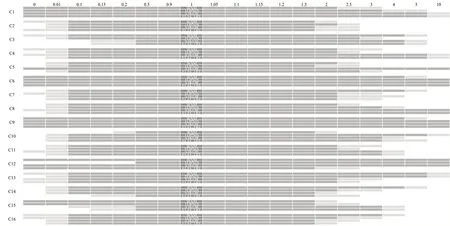
Fig.1 Sensitivity analysis of standard weight图1 标准权重的敏感性分析

接下来进行灵敏度测试，在测试过程中若排名不变，则灵敏度系数等于0；若备选方案的排序增加，并且另一个备选方案的排序减少，则此时的灵敏度系数为2。具体结果见表7-表9。

由表7-表9 可见，当标准权重增加或者减少5%时，对各方法产生的排名均未造成影响；当标准权重增加或减少50% 时，对各方法产生的排名均存在一定影响。其中，WSM 和TOPSIS 方法的影响较小，VIKOR 和 ELECTRE 方法的影响较大。

Table 7 Sensitivity test（standard weight change is 5%）表7 灵敏度测试（标准权重改变量为5%）

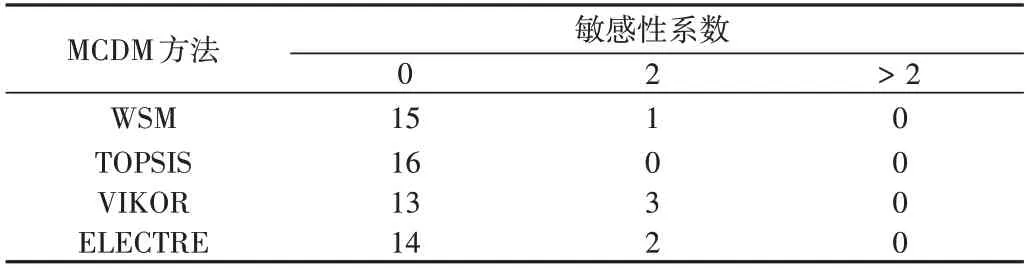
Table 8 Sensitivity test（standard weight change is-50%）表8 灵敏度测试（标准权重改变量为-50%）

Table 9 Sensitivity test（standard weight change is 50%）表9 灵敏度测试（标准权重改变量为50%）

6 结论

本文回顾了MCDM 方法在COVID-19 新冠肺炎疫情中的应用，确定了16 个标准，并使用WSM、TOPSIS、VIKOR和ELECTRE4种方法对中国5个省市及地区的抗疫水平进行排序。实验结果表明，传播控制是评价抗疫水平最重要的标准，其次是应急救援和疫苗研发；疫苗研究效率、区县封闭和城市封闭分别是标准中的重要因素；疫情传播控制的好坏也在一定程度上决定了抗疫水平的高低；经济和社会影响是标准中最后被考虑的因素。