面向不平衡数据基于高斯混合聚类的SMOTE改进算法

陶叶辉，赵寿为

（上海工程技术大学数理与统计学院，上海 201620）

0 引言

实际生活中，不平衡分类的场景出现在多方面，且不同类别的样本数量通常呈现高度的不平衡，如银行信贷［1］、癌症诊断［2］、网页检测［3］等。有关不平衡分类正成为数据分析中非常广泛的一类问题。不平衡学习问题处理主要从算法层与数据层两方面解决。现有的很多研究是通过对原数据进行处理来达到平衡，其中包括过采样、欠采样［4］、过采样与欠采样结合［5］3种方法。

过采样是通过对少数类样本进行简单复制达到与多数类样本的平衡，很容易导致过拟合问题。为此，Chawla等［6］提 出SMOTE（Synthetic Minority Oversampling Technique，SMOTE）算法，很大程度上避免了此类问题。该算法主要有两个缺点：①SMOTE 算法在选择K 近邻上具有一定的盲目性；②SMOTE 算法容易产生边缘化问题。

不少学者针对SMOTE 算法的不足进行了大量研究。钟龙申等［7］提出K-SMOTE 算法，将原始数据中的负类替换为“新增负类”，再利用SMOTE 算法得出新数据集，提高了分类性能；陈斌等［8］提出了KM-SMOTE 算法，使少数类数据集形成以簇为中心的数据聚集，有针对性地进行插值，提高了分类效果。针对K-means 算法存在初始中心选择不足等问题，郭朝有等［9］提出融合Canopy 和K-means 的SMOTE 改进算法，有效克服了K-means 算法初始中心选择随机性问题；楼晓俊等［10］通过引入“聚类一致性系数”和最近邻密度，使得合成的新样本更加均匀有效，提高了分类效果；韩旭等［11］提出了GMMUSA，在不改变类别空间结构基础上，删除多数类的冗余信息，提高了算法在信贷数据方面的分类性能。

以上文献均没有考虑少数类空间结构这一因素。因此，本文提出一种新的算法“GMM-SMOTE”。首先选择将高斯混合模型（Gaussian Mixture Model，GMM）算法运用于少数类样本集中，通过生成不同组数达到聚类目的；然后在保证少数类样本空间结构不变的情况下，删除与聚类中心点重叠的冗余样本；最后利用SMOTE 算法分别对不同的聚簇进行过采样，达到与多数类样本集样本量平衡的目的。采用UCI（University of California，Irvine）标准数据库［12］中的6 组数据集，基于随机森林（Random Forests，RF）分类器进行实验对比，结果显示本文模型的AUC 值平均提高6.09%，可以有效平衡不平衡的数据集。

1 SMOTE过采样

SMOTE 算法的基本思想是基于少数类样本随机插值生成新样本，即一种合成少数类的过采样技术算法。它是对以往随机过采样的一种改进方法，能有效解决传统采样方法容易发生过拟合的问题，提高了算法的泛化能力。

SMOTE 算法步骤如下：①对少数类的每一个样本xi，计算其到少数类样本集Smin中所有样本的欧式距离，得到k 近邻；②根据样本不平衡比例设置采样比例以确定采样倍率，对每个少数类样本xi从其k 个近邻中随机选择若干个样本，假设选择的近邻为xold；③对每个随机选择的近邻xold，分别与xi按照随机插值公式（1）生成新的样本xnew，最终合成一个插值样本均衡数据集。

其中，随机插值公式为：

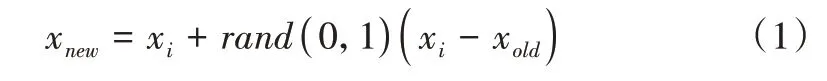
式（1）中，rand(0，1)表示(0，1)区间的随机数。

2 肘部法则及GMM-SMOTE过采样算法

本文提出的GMM-SMOTE 过采样算法是在传统SMOTE 算法基础上引入高斯混合聚类思想。同时，以肘部法则确定高斯混合聚类的初始组数，即聚簇数。下面从肘部法则、高斯混合模型、GMM-SMOTE 算法步骤3个方面分别阐述。

2.1 肘部法则

肘部法则（Elbow Method）通常被用于K-means 算法［13］中，根据每个簇与簇内样本间的和方差（SSE）来反映簇内结构情况。线条畸变程度高低代表簇内样本的空间变化，畸变程度越高，说明簇内结构越松散，反之则越紧密。当某个k 点的畸变程度开始明显变缓时，此点通常为最佳组数点［14］。如图1所示，当k=3时，其为最佳聚类组数。

Fig.1 Elbow method description图1 肘部法示意

2.2 高斯混合模型

高斯混合模型GMM 是由k个单高斯分布模型根据一定的权重组合而成［15］。每个高斯分布可称为一个组数（Component），这些组数线性加成组成GMM 的概率密度函数公式如下：

2.3 GMM-SMOTE算法步骤

实验前，先对实验数据进行预处理。采用10 折交叉验证［16］将不平衡数据样本集X划分为训练样本集S和测试样本集T。将训练集S分成二分类问题：多数类样本集Smax，所含样本数为Nmax；少数类样本集Smin，所含样本数为Nmin。GMM-SMOTE 算法流程如图2所示。

（1）采用GMM 聚类对少数类样本集Smin中的冗余样本进行删除。

对样本集Smin进行GMM 聚类，聚簇中心点为Ck，定义与中心点存在重叠的样本点为冗余样本并将其删除。

其中，设定冗余样本个数删除的阈值为：

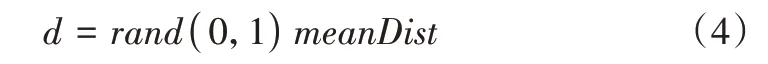
式（4）中，meanDist表示其聚簇中心点Ck到其样本集Smin中其他样本点xi的平均距离，其表达式为：

Fig.2 Synthetic new samples based on GMM-SMOTE algorithm图2 基于GMM-SMOTE算法合成新样本

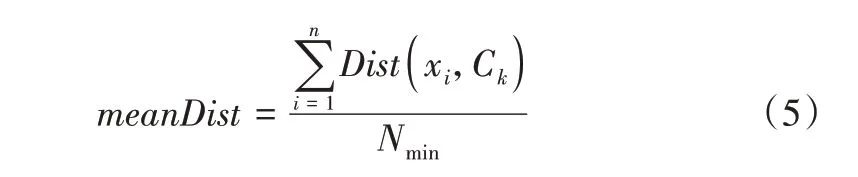
式（5）中，Dist(xi，Ck)为聚簇中心点Ck到其他样本点xi的距离。

输入：训练样本集S，GMM 聚类的组数k，冗余样本个数n；

输出：已被删除冗余样本后的少数类样本集Snew。

详细流程如下：①利用肘部法则确定最佳组数k，得到簇数k1、k2、k3......；②对于每个簇集，利用公式（4）和（5）删除冗余样本。

（2）对少数类进行过采样，合成少数类样本集Snewmin。

输入：样本集Snew

输出：平衡后的新样本集Xnew

流程：①利用公式（1）对完成步骤（1）后的样本集采用SMOTE 过采样算法生成Snewmin；②合并Smax与Snewmin形成新样本集Xnew。

所需过采样数量为：

3 实验结果与分析

3.1 数据集介绍

实验采用来自UCI 数据库中的6 组标准公开数据集，分别为Balancescale、CMC、Vehicle、G-lass、Haberman、Aggregation，且通过10折交叉验证（10-fold cross validation）估计算法精度。实验前需对原数据集进行处理，将多类别数据集分成二分类数据集。本文共采用8 组不同平衡度的数据集，如表1 所示。Balancescale0 数据集将类别3、1 合并为多数类，类别2 为少数类；Balancescale1 数据集将类别2、3 合并为多数类，类别1 为少数类；CMC0 数据集将类别1、3 合并为多数类，类别2 为少数类；CMC1 数据集将类别1、2 合并为多数类，类别3 为少数类；Vehicle 数据集将类别1、2、3合并为多数类，类别4为少数类；Glass 数据集将类别1、3、4、5、6 合并为多数类，类别2 为少数类；Haberman 为二分类数据集；Aggregation 数据集将类别2、3、4、6、7 合并为多数类，其余为少数类，具体如表1所示。

Table 1 Eight groups of two-category data表1 八组二分类数据

3.2 评价指标

评价分类器性能常用指标有准确率（accuracy）、精确率（precision）、召回率（recall）、F1-score、AUC（area under ROC curve）和ROC 等［17］。对于不平衡二分类问题，准确率是无法衡量分类器性能优劣的。由于不平衡二分类的复杂性，本文选择几何均数G-mean 和AUC 值作为评价分类器优劣的指标［18］，采用混淆矩阵来表示分类结果（本文假设少数类为正例，多数类为负例）［19］，如表2所示。

混淆矩阵仅仅统计了分类结果个数，难以衡量模型优劣。

基于混淆矩阵表2，可以得到召回率（recall）、特异度（specificity）、G-mean 等指标。

Table 2 Confusion matrix表2 混淆矩阵

少数类召回率：

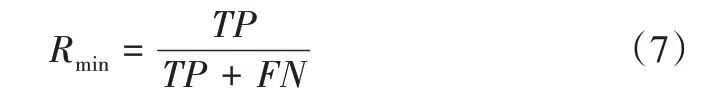
多数类召回率：

本文选择的几何均数G-mean：

AUC 值是基于ROC 曲线得到的。以两个分类器为例，若其中一条ROC 曲线完全包住另一条，则前者分类效果优于后者；若二者相交，则无法通过ROC 曲线直接得出。因而，引入AUC 值，即利用ROC 曲线下的面积来进行比较［20］。

3.3 结果分析

为了横向比较GMM-SMOTE 算法的性能优劣，选择以随机森林（random forests）为分类器进行3 组实验：①随机森林算法对未进行平衡处理的数据集进行分类；②先利用SMOTE 过采样算法对原始不平衡数据集进行处理，变为平衡数据集后，再利用随机森林算法进行分类；③先利用GMM 聚类算法对少数类数据集进行聚类，删除冗余样本点之后，再通过SMOTE 过采样算法以不同聚簇为单位生成人工样本点，使数据集平衡，最后利用随机森林算法进行分类。

表3 为8 组不同数据集在RF、SMOTE+RF 以及GMMSMOTE+RF 3种算法下的性能表现。

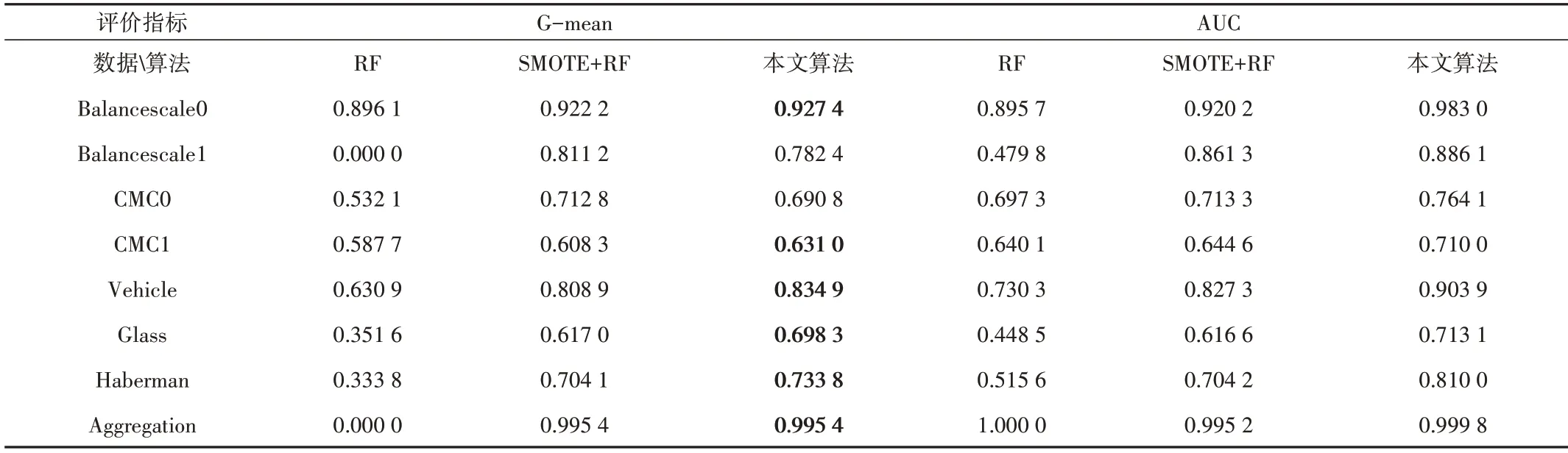
Table 3 Comparison result of RF，SMOTE+RF and the algorithm proposed表3 本文算法与RF、SMOTE+RF比较结果

分析表3可知：

（1）在8组数据集中，GMM-SMOTE+RF模型的Gmean 值有6 组数值（已加粗标记）高于或等于RF 和SMOTE+RF 两种模型，AUC 值均优于其他两种模型。相比于传统模型SMOTE+RF，本文模型的AUC 值平均提高了6.09%，有较好表现。

（2）Aggregation数据集中，GMM-SMOTE算法的Gmean 值持平于SMOTE 算法，但AUC 值相对较高。GMMSMOTE 算法在Balancescale1 和CMC0 两个数据集的Gmean 值略低于SMOTE+RF。另外，Balancescale1 和Aggregation 两个数据集基于RF 模型的G-mean 值为0，且Aggregation 数据集的AUC 值为1。对于高不平衡数据集，RF 算法不稳定，容易造成过拟合问题，分类效果差。

4 结语

传统的分类算法更多考虑的是类间不平衡，而对于类内不平衡的研究较少。本文提出一种基于GMM 聚类的过采样算法，能较好地处理类内不平衡问题。利用GMM 算法先聚类后插值，与传统SMOTE 算法相比插值更具有针对性，避免了新生成偏颇的数据而造成的过拟合问题。在保证少数类样本空间结构不改变的情况下，删除与聚类中心点重叠的冗余样本，极大保留了少数类样本的关键信息。采用UCI 标准数据库中的6 组数据集基于随机森林分类器进行实验对比，结果表明，本文GMM-SMOTE 算法比传统算法表现更优。

本文基于公开数据集验证了GMM-SMOTE 算法能提升分类效果。但该算法还有一些不足，如冗余样本的删除需要不断去调试删除的个数，具有一定的随机性。因此，本文算法仍需进一步改进。