基于Bi-LSTM的呼吸预测算法研究

王凯龙，常兆华，叶 萍

（上海理工大学健康科学与工程学院，上海 200082）

0 引言

目前在全球范围内，肺癌仍是癌症中死亡率最高的疾病之一［1］，近年来以灭活肿瘤细胞为目的的冷冻消融治疗手段引起了人们的广泛关注。该治疗手段需在CT 引导下做氩氦刀经皮穿刺，精准穿刺是治疗的重要条件，但胸腹部肿瘤的位置会随着患者的呼吸发生运动，这种运动会影响穿刺的精准度，在有些情况下肿瘤运动会达到28mm［2］。研究表明，胸腹部外部呼吸信号与肺部肿瘤运动具有良好的相关性，因此利用外部信号跟踪肺部肿瘤位置是可行的［3］。但是由于外部运动信号的获取、软件内部算法的运行以及机械臂延迟而导致的系统延迟会影响呼吸跟踪的实时性［4］，通常这种系统延迟在200ms 左右［5-7］，这会降低机器人的穿刺精度。Ma 等［8］研究表明，利用呼吸信号进行预测的方法能够有效提升穿刺机器人的穿刺精度，他们利用呼吸预测模型对公共数据集中的呼吸信号进行预测，并用运动体模进行穿刺实验，结果表明，预测结果的平均均方根误差（Root Mean Squared Error，RMSE）为0.58mm，穿刺误差的平均均方根（Root Mean Square，RMS）为0.65 mm。

有关呼吸跟踪和呼吸预测的研究在放疗中展开较早，Hoogeman 等［9］的研究表明，使用呼吸跟踪和呼吸预测技术能够有效地减少由呼吸运动和系统延迟引起的几何误差。比较经典的呼吸预测算法有：CyberKnife®的Synchrony®呼吸同步跟踪系统使用的预测算法、支持向量机（Support Vector Machine，SVM）、自回归移动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）和神经网络。

Synchrony®系统在临床实践中表现良好，其利用两个正交的kV 级X 射线系统等中心地投射到患者的治疗部位观测内部肿瘤运动并建立与外部光学标记相关的运动模型，然后使用呼吸预测技术补偿固有的系统延迟［10-11］。Synchrony®呼吸同步跟踪系统应用了一种混合预测算法，该混合算法结合了线性算法、模式匹配和模糊逻辑3 种方法［12-13］。支持向量回归（Support Vector Regression，SVR）是SVM 的一个应用分支，Riaz 等［14］利用SVR 方法对肿瘤运动进行预测，在延迟为1s 的状态下预测结果的RMSE 在2mm以内。Khashei 等［15］研究表明，ARIMA 在时间序列预测方面表现良好，Ichiji 等［16］使用ARIMA 结合多层感知器（Multilayer Perceptron，MLP）对肿瘤运动进行预测，其结果显示平均绝对误差（Mean Absolute Error，MAE）在500ms 的延迟下为0.795 3±0.024 3 mm。Wang等［17］应用七层双向长短期记忆神经网络（Bidirectional Long Short-term Memory，Bi-LSTM）预测呼吸运动信号，设定延迟为400ms 的情况下其预测结果的平均RMSE为0.097 mm、MAE为0.074 mm。

很多相关研究实验所用的呼吸数据样本数量过少，或仅截取呼吸平稳的区段进行实验，无法测试模型的鲁棒性。本文使用了29 组呼吸数据进行实验，在保证样本数量的同时不特意截取呼吸平稳区段，使实验结果更贴近临床需求。本文提出的基于Bi-LSTM 的呼吸预测模型框架不但具有很高的准确性，而且在面对各种复杂呼吸状况时也表现出了较好的鲁棒性。

1 实验数据

1.1 数据获取及预处理

实验中，使用NDI Polaris 光学定位系统采集了23 组志愿者的外部呼吸数据，该系统通过追踪仰卧状态下的志愿者胸腹部体表的红外光学定位支架以获取呼吸数据，系统采样频率设定为20Hz，每组的采样时间为5～7min，采集到的每组数据包括呼吸运动的左右、头脚、前后3 个维度。志愿者在呼吸数据采集过程中完全处于自由呼吸状态，因此数据中包含了基线漂移、呼吸频率改变、深呼吸等状态。此外，实验还加入了德国Lubeck 大学机器人与认知系统研究所公开数据库中的6 组呼吸数据，该数据的志愿者均在肺部有恶性肿瘤。

为了方便实验结果的比较并保证实验数据可靠，本文中统一选取前后方向的数据进行预测，且并不特意截取呼吸数据的平滑段进行试验，保留原数据的诸多不利于预测精度的状况，29组数据均截取6 000个数据点进行实验。

采集的原始呼吸数据的噪声严重影响了之后数据训练效果，因此实验开始时需对每条数据进行平滑降噪处理，在保证呼吸数据原有特性不变的前提下降低信噪比。本文选用Savitzky-Golay 滤波器对原始数据进行平滑降噪处理。

采集到的原始呼吸数据的数值分布并不统一且数值较大，因此还需对呼吸数据作归一化处理，其目的是在统一量纲的同时便于梯度下降的计算、加快训练模型的收敛。实验中采用Z-Score 方法对平滑降噪后的数据作标准归一化处理，并在模型训练完成后将数据去标准化。

1.2 训练样本构建

因每位志愿者的呼吸运动幅值、频率等诸多因素不同，甚至同一人在不同时间所测得的呼吸数据亦大不相同，在呼吸预测中应保证数据时效性，因此每组呼吸数据都需要构建相应的训练样本。

将每条经过标准归一化后数据的前80%作为训练集，后20%作为验证集。将预测时长设定为250ms，能够补偿大部分系统的延迟时间。自测呼吸数据的采样频率为20Hz，德国Lubeck 大学公开数据集中的呼吸数据采样频率也为20Hz 左右（17.5～21.3Hz），即预测步长为5。实验设定通过前50 个数据点的位置变化预测后5 个数据点的位置信息。

利用滑动窗口将训练集X=[x1，x2，x3，…，xend]构成有效的训练样本，即输入矩阵Input和输出矩阵Output。滑动窗口构建训练样本的过程如图1 所示。输入步长为50，预测步长为5，从训练集X中的x1开始将50 个数据点设定为输入矩阵Input的第一列，从x51开始将5 个数据点设定为输出矩阵Output的第一列，随后滑动窗口右移继续采样。输入矩阵Input和输出矩阵Output如下：

Fig.1 Schematic diagram of sliding window图1 滑动窗口示意图

式（1）、式（2）中，n代表滑动窗口右移的步长，每一个训练集X可构建k+1组训练样本。

2 预测模型

2.1 LSTM 模型

循环神经网络（Recurrent Neural Network，RNN）在时间序列数据预测方面有着较好的表现并且广泛应用于多个领域，但因梯度消失或爆炸问题，RNN 在处理长距离依赖问题上的能力有限。Hochreiter 等［18］提出的长短期记忆网络（Long Short-Term Memory，LSTM）引入记忆单元和遗忘门，克服了RNN 的局限性。如图2 所示，LSTM 有4 个门，即输入门i、遗忘门f、控制门c和输出门o［19］。

输入门决定哪些信息可以传递给单元格，定义为：

遗忘门决定了输入中的哪些信息应该从先前的记忆中忽略，定义为：

控制门控制单元状态从Ct-1到Ct的更新，如式（5）、式（6）：

输出门负责生成输出和更新隐藏向量ht-1，定义为：

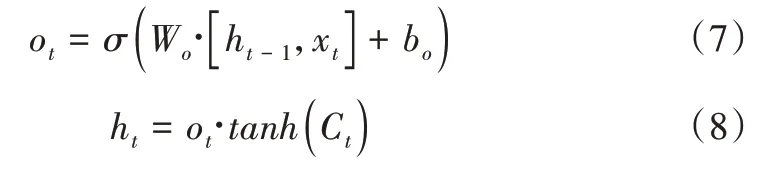
其中，σ是Sigmoid 激活函数，W是相应的权重矩阵，tanh用于将值缩放到-1～1的范围内。

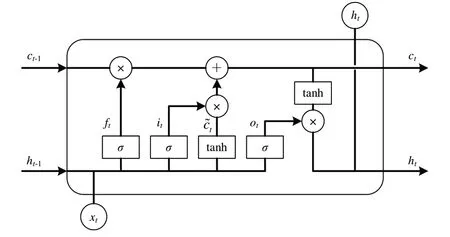
Fig.2 LSTM unit structure图2 LSTM 单元结构

2.2 Bi-LSTM 模型

Bi-LSTM 属于双向循环神经网络（Bi-RNN）的一种，Bi-RNN 于1997 年由Schuster［20］首次提出。Bi-RNN 结构如图3 所示，由两个正负时间方向的RNN 叠加而成，前向状态和后向状态连接在一个输出层，在训练过程中Bi-RNN 在前向和后向两个方向同时进行训练。Bi-RNN 的结构决定了每一时刻的输出都能获取整个输入序列的完整信息而不仅仅是当前时间之前的信息。这种双向结构可以应用于RNN 的变种网络，本实验中就使用了Bi-LSTM。

Fig.3 The general structure of BRNN图3 BRNN的一般结构

3 实验结果与分析

3.1 实验平台及评价标准

本实验基于MATLAB 平台利用29 组呼吸数据对LSTM、门控循环单元（gated recurrent unit，GRU）、Bi-LSTM 3 种算法进行对照比较。实验用计算机装有Intel（R）Core（TM）i7-9750H CPU 和NVIDIA GeForce GTX 1650 GPU。

利用RMSE 和MAE 作为主要的实验结果评价标准，RMSE 表示预测值和真实值之间残差的样本标准差，MAE表示预测值和观测值之间绝对误差的平均值。

式（9）、式（10）中，N代表呼吸样本数据点个数，xi代表呼吸样本数据点的实际值，ˉxi代表该点的算法预测值。此外，本实验还统计了每一例样本预测结果中误差大于0.5mm 的数据点个数。

3.2 模型参数实验

首先，对滑动窗口右移的步长n 取何值做了实验比较，结果如图4 所示。横坐标表示制作训练集时滑动窗口右移的步长，纵坐标表示不同n 值时的预测精度。选用样本1 进行实验，预测算法采用LSTM。实验结果显示，其RMSE 与MAE 均呈现先减小后增大的趋势，可观察到当滑动窗口右移步长为5 时，RMSE 与MAE 最小，预测效果最佳。

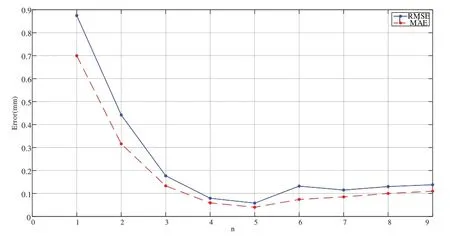
Fig.4 Experiment of sliding window right step size n图4 滑动窗口右移步长n实验测试

Fig.5 Experiment of network layer’s number图5 网络层数实验测试

其次，对预测模型中的网络层数设置进行实验，实验结果如图5 所示。实验选用样本5 进行，预测算法采用Bi-LSTM。横坐标表示从1 至5 不同的Bi-LSTM 网络层数，纵坐标表示不同网络层数的预测精度。可以明显看出，随着网络层数的增加，虽然网络结构逐渐变得复杂，但RMSE与MAE 却呈现上升趋势，因此当预测算法的网络层数为1时，预测效果最佳。

构建训练集时，n 越小所得到的训练样本更多，但却导致样本特征不明显，在网络训练中很容易导致网络过拟合。因此，设置合适的n 值不但能减少训练时长，还可提高预测准确性。设置网络层数时发现更深的网络层使预测精度下降且徒增训练时长，得出复杂的网络结构并非适用所有情况，本实验中隐藏层设为单层预测效果最佳。此外，本实验中网络模型的超参数如下：训练次数、神经元个数、批处理大小、初始学习率、学习率下降因子、下降迭代次数、求解器分别为350、200、all group、0.002、0.1、250、adam。

3.3 呼吸数据预测实验

表1 对29 组呼吸数据预测结果的RMSE 进行统计并在结尾作平均值计算。相较于LSTM、GRU，Bi-LSTM 算法的平均值更小。29 组数据中有19 组，Bi-LSTM 算法预测结果的RMSE 小于LSTM、GRU。

Table 1 RMSE statistics of prediction results（mm）表1 预测结果的RMSE统计（mm）

表2 对预测结果的MAE 进行统计并在结尾作平均值计算。29 组数据中，Bi-LSTM 算法预测结果的MAE 均小于LSTM、GRU。并且，Bi-LSTM 算法预测结果MAE 的平均值明显小于LSTM、GRU。

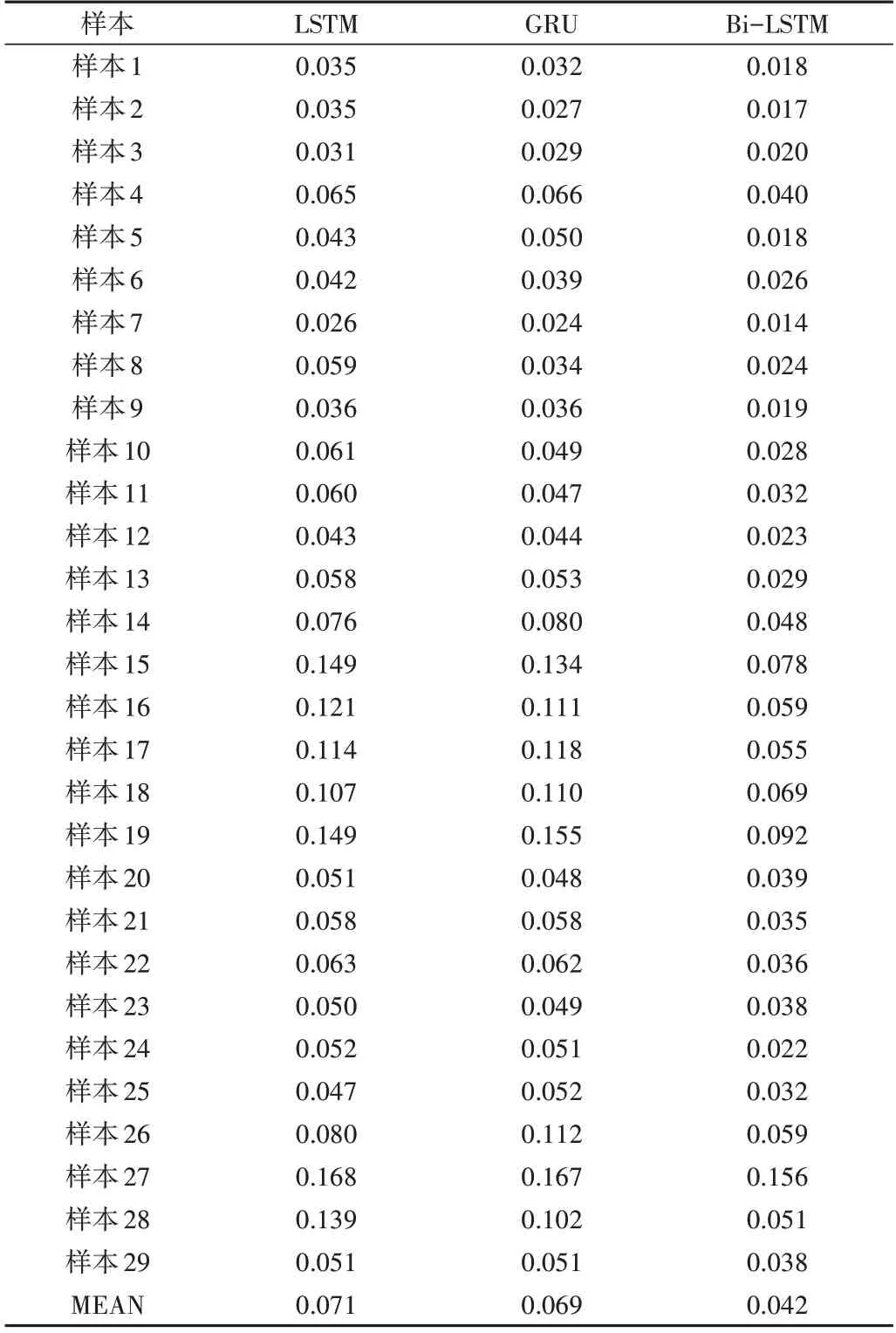
Table 2 MAE statistics of prediction results（mm）表2 预测结果的MAE统计（mm）

此外，针对临床关注的预测误差略大情况出现的次数也做了统计，结果如表3 所示。表3 中统计了预测结果中误差大于0.5mm 的个数，29 组数据中的18 组，Bi-LSTM 算法预测结果中误差大于0.5mm 的个数小于LSTM、GRU，且Bi-LSTM 算法在该统计中平均值亦最小。

图4 中展示的呼吸数据其呼吸频率与幅值均不稳定，且具有较为明显的基线漂移；图5 中展示的呼吸数据其呼吸状态较为稳定，频率与幅值均无较大变化。此外，图6-图7 分别直观展示了两组呼吸数据应用不同算法的预测结果。横坐标表示呼吸数据的点数，纵坐标表示呼吸位置数据，蓝色实线代表真实值，橙色实线代表预测值（彩图扫OSID 码可见）。可以直观看出，LSTM 与GRU 算法的预测结果中，在呼吸的波峰和波谷处均有小幅度的摇摆，Bi-LSTM 的预测结果更拟合于真实值且更为平滑，明显优于LSTM 与GRU。

对实验结果进行分析，从RMSE、MAE 和误差大于0.5mm 的数据点个数这3 个参考标准可知，各项指标Bi-LSTM 最佳。并且，通过直观观察发现，在预测较不稳定的呼吸数据时Bi-LSTM 算法依然结果较好。与很多相关研究相比，本实验并没有特意截取呼吸数据中较平稳的区域进行实验，而是将诸多不利因素（如呼吸频率、幅值明显变化，基线漂移等）都考虑在内，在比较准确性的同时也验证了算法鲁棒性，使结果更贴近临床需求。

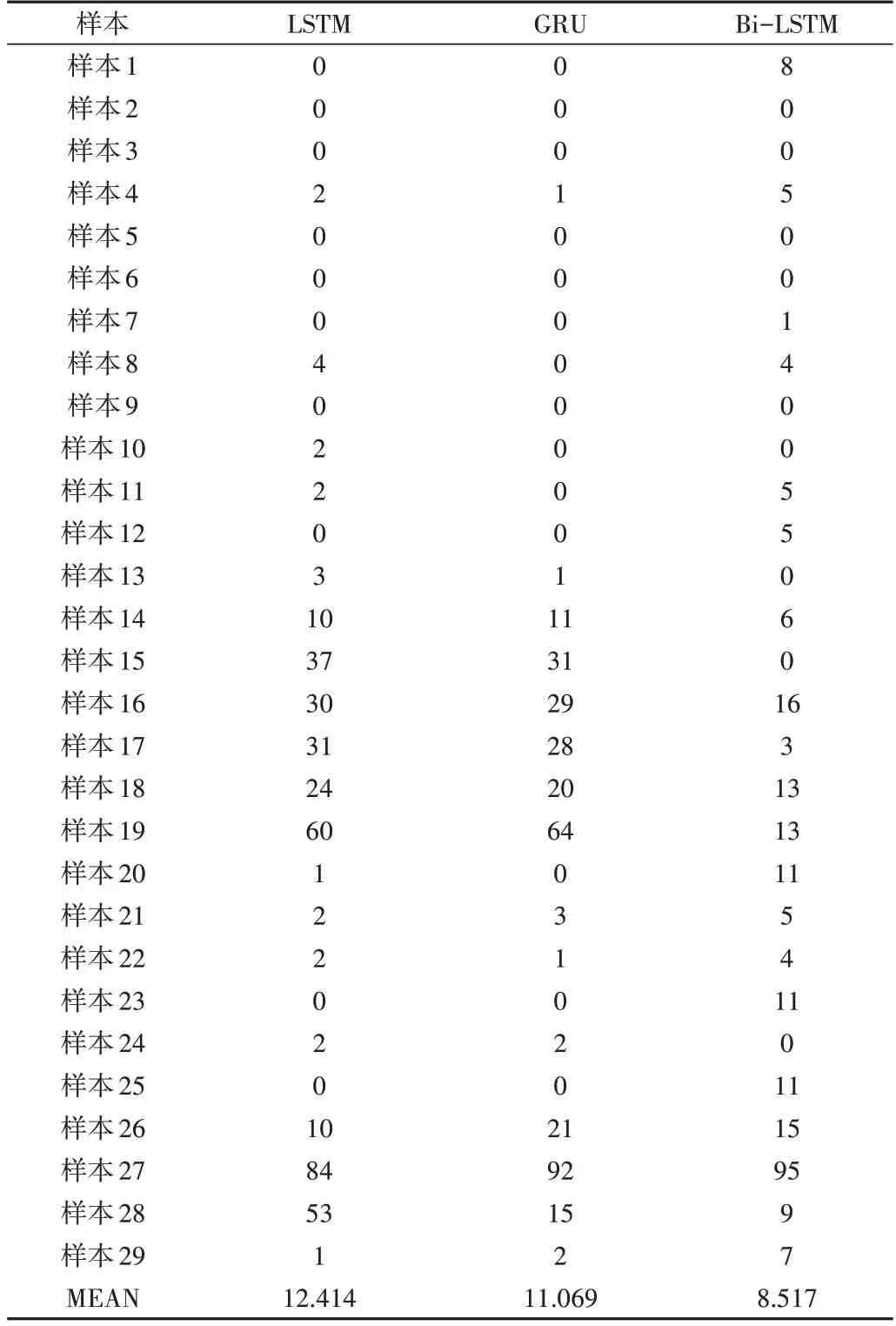
Table 3 Statistics of number of data points with error＞0.5mm表3 误差＞0.5mm的数据点个数统计

Fig.6 Examples of unstable breathing data prediction results图6 不稳定呼吸数据预测结果示例

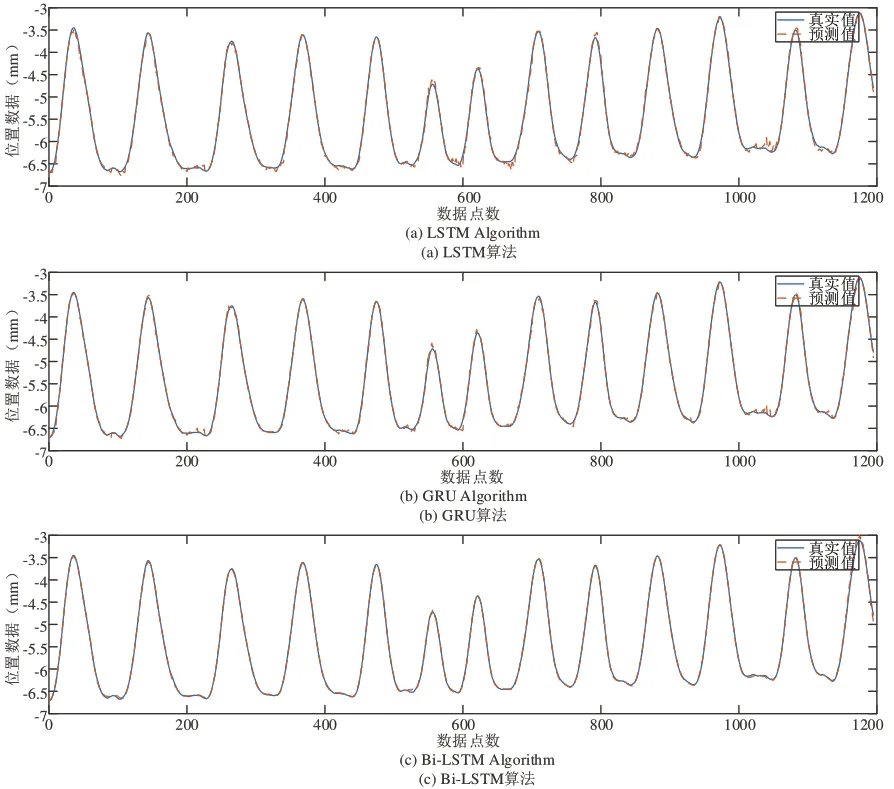
Fig.7 Examples of relatively stable respiratory data prediction results图7 较稳定呼吸数据预测结果示例

4 结语

本文提出一种基于Bi-LSTM 的呼吸预测模型框架，调整优化了模型各参数后用29 组数据进行实验。实验结果表明，其在250ms 的延迟下平均RMSE、MAE 分别为0.091mm、0.042mm，在提高预测准确性的同时也具有较强的鲁棒性，能够应对复杂的呼吸状况。并且，其单层隐藏层的网络结构使得训练速度很快，具有一定的临床应用可行性。后续将从如下方面进行深入研究：①建立内外呼吸关联模型；②搭建仿真穿刺实验平台；③进行仿真穿刺实验。