BOOST峰值电流型PFC变换器的稳定性分析
2022-05-26王晨皓陈艳峰
王晨皓 陈艳峰

摘 要:以BOOST峰值电流型PFC变换器为研究对象,采用数值仿真法和解析建模法对其进行建模及稳定性分析。首先通过MATLAB/Simulink应用软件建立BOOST峰值电流型PFC变换器的电路模型,通过仿真研究其分岔现象,然后建立离散映射方程,并由雅可比矩阵法来分析分岔现象,从而得出各参数的稳定边界。其结果可为BOOST峰值电流型PFC变换器的设计、运行提供依据。
关键词:功率因数校正;稳定性分析;分岔现象;频闪映射;雅可比矩阵
中图分类号:TM46 文献标志码:A 文章编号:1671-0797(2022)10-0008-04
DOI:10.19514/j.cnki.cn32-1628/tm.2022.10.003
0 引言
BOOST峰值电流型PFC变换器是一种有源功率因数校正技术,能提高开关电源功率因数,节省能源,提高电能质量。该变换器由电感、电容、开关管等元件组成,是时变非线性系统,具有很强的非线性,存在分岔现象[1],当电路参数变动经过分岔点时,系统的定性性态(如平衡状态或周期运动的稳定性等)会发生突然变化,引发不稳定现象。在设计开发此变换器时,为了抑制分岔现象,保证电路能在开关频率下稳定运行,有必要开展对此类电路的分岔研究,了解电路各参数的稳定边界及不稳定现象,为设计开发提供理论依据。BOOST峰值电流型PFC变换器存在慢时标分岔及快时标分岔两种分岔现象,本文仅研究其快时标分岔。
本文以BOOST峰值电流型PFC变换器为研究对象,采用数值仿真法和解析建模法对其进行建模及稳定性分析。首先通过MATLAB/Simulink应用软件建立电路模型,通过仿真研究分岔现象,然后建立离散映射方程,并由雅可比矩阵法来分析分岔现象,从而得出各参数的稳定边界。
1 采用数值仿真法分析BOOST峰值电流型PFC变换器的分岔现象
1.1 BOOST峰值电流型PFC变换器建模
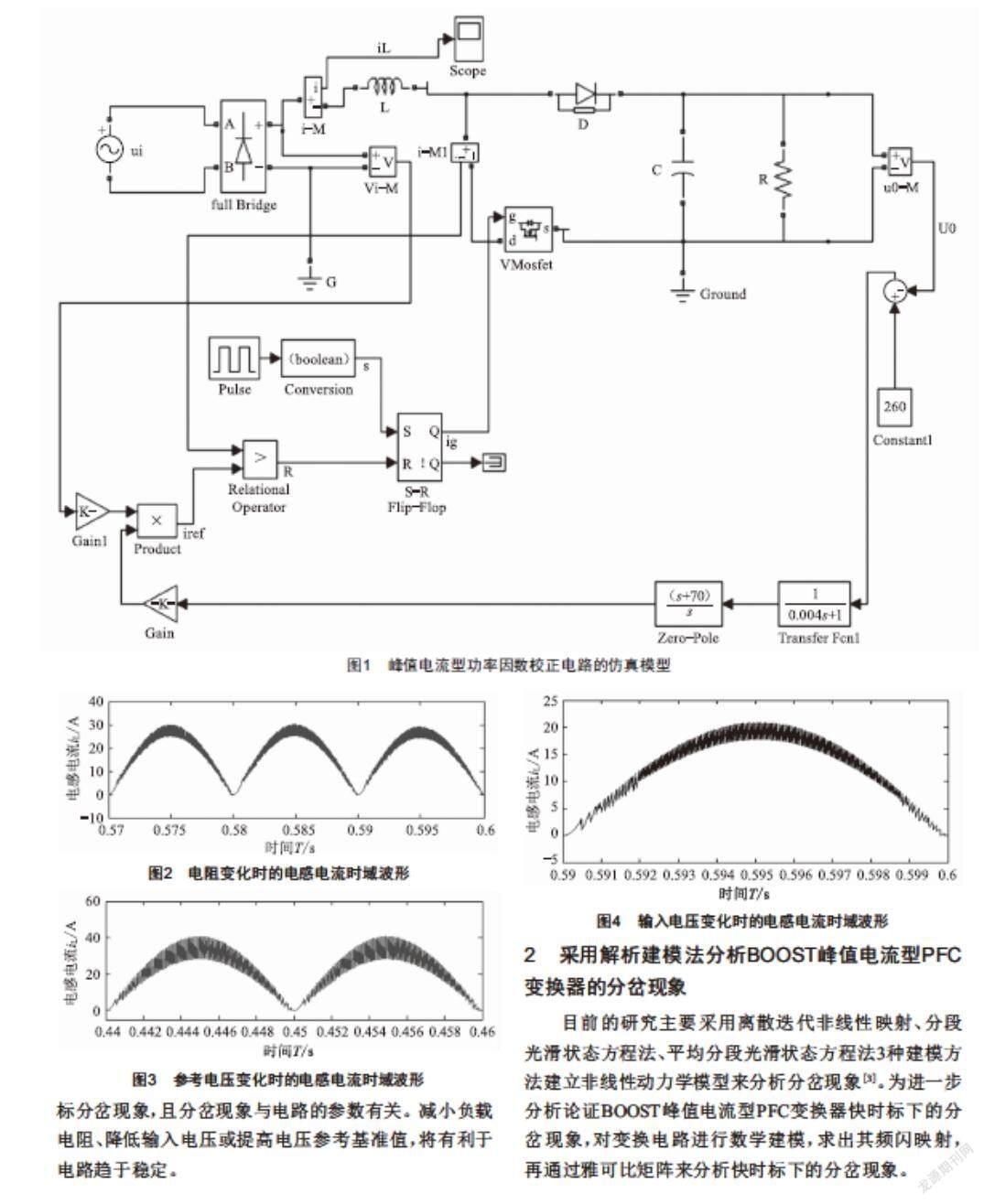
BOOST峰值电流型PFC变换器是一个时变网络,闭环工作时是时变非线性的。采用MATLAB软件的Simulink和SimPowerSystems工具箱进行数值仿真建模,搭建出了对应的Simulink仿真模型[2]。如图1所示,参数选取如下:在主电路中,输入电压频率f=50 Hz,电感L=2 mH,电容C=470 μF;在控制电路中,开关周期Ts=
20 μs,k1=0.08,k2=1/60,TF=4 ms,Tc=1/70 s。
1.2 分岔现象仿真及分析
为详细研究上述模型分岔现象,选择电阻、固定输入电压、参考电压其中之一作为唯一变量,研究其对应的分岔现象,即假定三个物理量电阻R、输入电压ui、参考电压Vref中的两个量不变,只有另一个发生变化时出现分岔现象。
1.2.1 电阻值变化时的分岔现象
固定ui=110 V,Vref=180 V,改变负载电阻进行仿真。当R=85 Ω时,出现分岔现象,iL的波形如图2所示。负载电阻值越大,分岔越严重,由周期1状态变为周期2状态(倍周期分岔现象),而且随着分岔的加劇,分岔点由两端向中间靠近,分岔的范围扩大。
1.2.2 参考电压Vref变化时的分岔现象
固定ui=130 V,R=95 Ω,改变参考电压进行仿真。当Vref=260 V时,出现倍周期分岔现象,电路工作在周期2状态。iL的波形如图3所示,减小Vref,发现分岔更加严重。
1.2.3 输入电压ui变化时的分岔现象
固定Vref=380 V,R=100 Ω,改变输入电压ui,对电路模型进行仿真。当ui=180 V时,存在倍周期分岔现象,电路工作在周期2状态。
iL的波形如图4所示,可见,在t=0.592 s之前和t=0.599 s之后,电感电流存在明显的倍周期分岔现象。进一步增加ui,发现分岔更加严重,电感电流存在明显的倍周期分岔现象。
1.2.4 小结
仿真发现,BOOST峰值电流型PFC变换器存在快时标分岔现象,且分岔现象与电路的参数有关。减小负载电阻、降低输入电压或提高电压参考基准值,将有利于电路趋于稳定。
2 采用解析建模法分析BOOST峰值电流型PFC变换器的分岔现象
目前的研究主要采用离散迭代非线性映射、分段光滑状态方程法、平均分段光滑状态方程法3种建模方法建立非线性动力学模型来分析分岔现象[3]。为进一步分析论证BOOST峰值电流型PFC变换器快时标下的分岔现象,对变换电路进行数学建模,求出其频闪映射,再通过雅可比矩阵来分析快时标下的分岔现象。
2.1 BOOST峰值电流型PFC变换器的频闪映射
以电路的开关频率为采样频率,在每个开关周期的起点对变换器状态变量进行采样,建立其频闪映射数学模型[4-5]。令初始时刻为nTs,此时电感电流iL为iL(n),电容电压uc为uc(n),输入电压ui为ui(n)。当开关频率fs足够高时,则可以认为在每个开关周期Ts内的输入电压ui为定值v。ui(n)=v(n)。
当ton>Ts时,在整个开关周期功率开关管都导通。
iL(n+1)=iL(n)+■·v(n)·Ts (1)
uc(n+1)=uc(n)·e■ (2)
当ton
iL(nTs+ton)=iref =iL(n)+■·v(n)·ton (3)
uc(nTs+ton)=uc(n)·e■ (4)
在nTs+ton—(n+1)Ts,功率开关管截止。
iL(n+1)=e■·[(p1q1+p2q2)·cos γ·tb+
(p1q2-p2q1)·sin γ·tb]+■ (5)
uc(n+1)=e■·(q1·cos γ·tb+q2·sin γ·tb)+v(n) (6)
式中:α=-■;γ=■;p1=■;p2=■;
q1=uc(n)·e■-v(n);q2=■。
当ton e■·[(p1q1+p2q2)·cos γ·tf+ (p1q2-p2q1)·sin γ·tf]+■=0 (7) 由此可求出tf。 在nTs+ton+tf—(n+1)Ts: iL(n+1)=0 (8) uc(n+1)=uc(n)·e■ (9) 通过定出状态变量的初始值,可求出下一周期的解,如此不断反复,最终得到所需精度的频闪映射的采样点的解。 2.2 离散映射的雅可比矩阵 雅可比矩阵是研究变换器非线性动力系统中局部分岔问题的一种解析法[4-5]。对于离散映射Xn+1=f(Xn,μ),在不动点xe处的雅可比矩阵定义为JF=■■。通过推算,BOOST峰值电流型PFC变换器的频闪映射雅可比矩阵为: JF=■ ■ ■ ■■ (10) 通过雅可比矩阵特征值轨迹可以较精确地计算出倍周期分岔点位置,根据映射的不动点方程稳定性定理,不动点的稳定性由其雅可比矩阵的特征值λ决定,当特征值λ=-1时,参数对应的值即变换器由周期1到周期2的分岔点,从而得出快时标下不稳定区域边界。因此,通过这种方法定位变换器的分岔点,就能得到电路可采用的参数范围,确保变换器稳定地工作在周期1区域。 2.3 分岔现象仿真及分析 2.3.1 BOOST峰值电流型PFC变换器的分岔现象 根据上述变换器的频闪映射,开展对快时标下的分岔仿真。当ui=220 V,R=200 Ω,Vref=380 V时,电感电流与输出电压的相图如图5所示,电感电流的采样值如图6所示。出现倍周期分岔现象,电路工作在周期2状态,可明显看出存在快时标下的分岔现象,且由于系统拓扑的变化,电路在模态1、2和模态3之间频繁切换,致使非线性现象变得更为復杂。电路存在倍周期分岔及其他分岔现象,甚至发生混沌现象。 2.3.2 BOOST峰值电流型PFC变换器的稳定边界 设定输入电压频率f=50 Hz,储能电感L=2 mH,电容C=470 μF,开关周期Ts=20 μs。通过上述频闪映射的雅可比矩阵表达式进行计算,得到特征值,从而得到系统的分岔点,最后形成不同电路参数下的稳定性边界。当ui=110 V时,Vref和R各分岔点形成的稳定性边界如图7所示;当R=80 Ω时,Vref和ui各分岔点形成的稳定性边界如图8所示。计算结果形成准确的稳定边界,这样可确保设计BOOST峰值电流型PFC变换器时,准确选择电路参数,避免变换器发生分岔,进入不稳定区域。3 结语 本文采用MATLAB对变换器进行建模及仿真,分析快时标下的分岔现象。接着采用频闪映射法和雅可比矩阵法对电路进行数学建模,并在仿真中进一步分析论证分岔现象,同时得到不同电路参数下的稳定性边界,为BOOST峰值电流型功率因数校正电路的设计、运行提供了依据。 [参考文献] [1] 陆启韶.分岔与奇异性[M].上海:上海科技教育出版社,1995. [2] DRANGA O,TSE C K,IU H H C,et al.Bifurcation Behavior of a Power-Factor-Correction Boost Converter[J].International Journal of Bifurc-ation and Chaos,2003,13(10):3107-3114. [3] 罗晓曙,汪秉宏,邹艳丽.DC-DC开关功率变换器的非线性动力学行为研究[J].力学进展,2003(4):471-482. [4] 马西奎,刘伟增,张浩.快时标意义下Boost PFC变换器中的分岔与混沌现象分析[J].中国电机工程学报,2005,25(5):61-67. [5] WU X Q,TSE C K,DRANGA O,et al.Fast-Scale Instability of Single-Stage Power-Factor-Correction Power Supplies[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2006,53(1):204-213. 收稿日期:2022-02-28 作者简介:王晨皓(1971—),女,河北澧县人,硕士,讲师,从事电力系统控制及通信电源等的教学和研究工作。 陈艳峰(1970—),女,湖南永兴人,博士,教授,从事非线性电路系统理论与功率电子学的研究工作。
