基于价值引领和素养提升的高等数学一流课程建设

林洁

摘  要：“数学素养”的提升与价值塑造相辅相成。针对现阶段我国工科院校学生“数学素养”相对缺乏的实际情况，本文指出了高等数学课程教学中一系列亟待改革的典型问题：“数学无用论”在学生中普遍存在;学生缺少独立思考和表达的机会;缺乏过程性考核及有挑战度的题目;重知识传授而轻育人。基于以上问题，本文在中法合作办学模式下“高等数学（6）”一流课程建设的过程中，提出并实践了一系列改革措施：依据课堂功能，科学设置班型;以提升逻辑推理能力为目标，开展教学活动;注重过程性考核，增加题目挑战度;突出价值引领，开展课程思政教学。

关键词：数学素养;价值引领;课程思政教学

中图分类号：G640    文献标识码：A    文章编号：1673-7164（2022）10-0038-04

一、高等數学课程教学中亟待解决的问题

齐民友教授指出：“数学作为文化的一部分，其最根本的特征是它表达了一种探索精神。”[1]顾沛教授说，数学不仅是一些知识，也是一种素养，即“数学素养”[2]。“数学素养”的提升有利于学生领会数学思想中蕴含的价值观。反过来，突出课程的价值引领又能促进“数学素养”的提升。但要想提升学生的数学素养，我国高等数学课程教学中还存在一些亟待改进的问题。

（一）“数学无用论”在学生中普遍存在

目前，大部分工科生还只是把数学作为一种“工具”，认为学数学的目标只是学会套用公式、会计算即可，感受不到数学的更多用处。因此高校有必要在数学课堂中注重学生数学素养的提升，让学生领会到数学所表达的“探索精神”。

（二）学生缺少独立思考和表达的机会

上课时，很多学生感觉一听就懂，可是自己做题时，却不知该从何下手，也不会用数学语言来表达。这类学生缺乏独立思考和表达的能力。针对此类学生，教师应制定相应的教学策略。

（三）缺乏过程性考核及有挑战度的题目

目前，大多数高校高等数学课程的考核，都是平时成绩与期末成绩相结合。而且，考试的题型基本上是在例题或练习题的基础上稍做改动，真正需要灵活推理的题型并不多。这种考核方式的问题在于一些学生不能及时发现自己的问题，教师也不能及时给予关注，考试成绩未能体现学生的能力。

（四）重知识传授而轻育人

很多教师会因为课时紧张、知识点讲不完，认为没有时间做思政教育。然而，对于学生而言，相比学习知识，更重要的是学做人。尤其是在中外合作办学机构中，课程育人方面的工作更是必不可少。为了在课时紧张的条件下最大程度地实现课程育人的功能，教师在课程建设过程中要仔细挖掘能够与思政教育相结合的知识点，在知识传授的过程中，润物无声地完成育人目标。

二、改进措施

“高等数学（6）”是中欧航空工程师学院（以下简称“中欧学院”）开设的一门重要基础课，将为学生后续学习专业基础课及相关专业课打下必要的数学基础，为其提供必需的数学概念、理论、方法、运算技能和分析、解决问题的能力及素质。课程不同于国内一般的高等数学课程，是法国工程师预科数学教学模式本土化的成果，强调所有数学知识的整体性以及数学各个分支的联系，更加注重培养学生的逻辑严谨性和知识的综合运用能力。

课堂教学是课程思政建设的主渠道[3]。教师要在教育教学方法上不断改革创新，以学生的学习成效为目标，深入开展以学生为中心的教学方式和学业评价方式改革，激发学生学习兴趣，引导学生深入思考，实现思想启迪和价值引领。针对以上问题，该课程采取了以下几种改革措施：

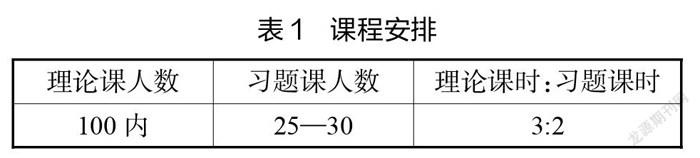
（一）依据课堂功能，科学设置班型

习题课是理论知识的实践平台，通过做题，学生能够找到知识漏洞，练习数学语言的表达。与同类课程相比，本课程设置了更多的习题课课时，并且实行小班授课。

习题课小班授课的优点在于能增加师生互动，为学生提供更多自主思考的空间。基础性习题由学生轮流讲解，以达到锻炼学生表达能力和简明、严密的语言组织能力的目标。

（二）以提升逻辑推理能力为目标，开展教学活动

“数学素养”的通俗说法是“把所学的数学知识都排除或忘掉后，剩下的东西”，例如从数学角度看问题的出发点;有条理的思维，严密的思考、求证;简洁、清晰、准确的表达;在解决问题、总结工作时，逻辑推理的意识和能力;对所从事的工作做到合理的量化、简化、周到的运筹帷幄[2]。

“数学素养”很重要的一方面就是熟练运用准确、简明、规范的数学语言表达自己的数学思想[2]。为此，教师在平时的作业和考试中，对于学生在数学语言的准确表达、规范书写方面应严格要求。教学过程中注重学生数学语言表达能力、严谨思维、抽象思维和逻辑推理能力的培养。

同时，教师应设计难度更高、范围更广、趣味性更强的大作业，培养学生数学知识的综合运用能力和创新思维能力。大作业通常是一套综合性很强的题目，一般围绕一个主题展开，可能是著名定理的证明，也可能是新概念的性质的研究。教师可在中间设计小题，引导学生最终解决该问题。小题通常是以一章所学内容为主要工具，也会用到之前的基础知识。大作业对学生知识的融会贯通、综合运用有更高的要求。题目的设计对教师有较高的要求，可以在学术研究、科技发展前沿成果的基础上进行改编。

（三）注重过程性考核，增加题目挑战度

课程的考核成绩组成为：作业10%、期中考试成绩40%、期末考试成绩50%。

作业并非提交后就能得满分，而是要根据答题情况得分。所以，学生要想拿到较高的作业分数，必须认真思考，给出完善解题思路。

不同于通常的考试，期中和期末考试时长都是3—4小时，题型与大作业类似，题目综合性很强，考查学生对知识掌握的系统性和独立解决问题的能力。该课程的考核方式更注重学生平时的积累，考试题型对学生的能力有更高要求。

（四）突出价值引领，开展课程思政教学

为了提升学生的“数学素养”，教师可以在高等数学课堂中传播数学文化，在传播数学文化的过程中自然地渗透价值引导：教师可以带领学生学习数学家身上的崇高道德和高尚品质以及他们在攻克数学难题的过程中表现出的科学态度和精神;在数学问题的证明中贯穿辩证唯物主义观点的方法，例如理论与实践的统一、事物的普遍联系和系统思维、永恒发展和创新思维等。这些方面都契合了课程思政内容的要求。适时在课堂中融入思政元素，既能加深学生对知识的理解，提高学习兴趣，又能起到课程育人的作用。

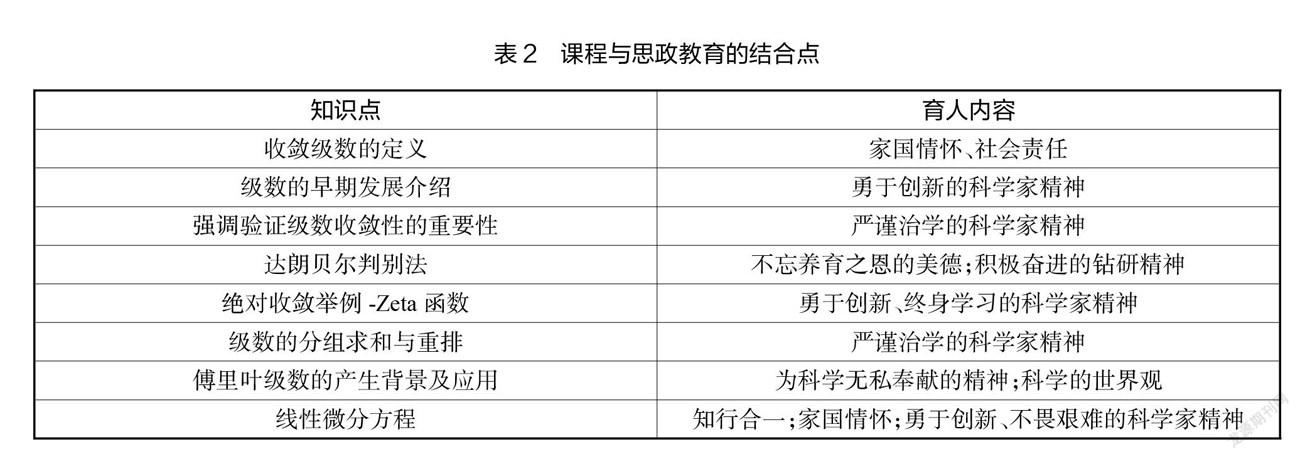
1. 课程与思想政治教育的结合点

《高等学校课程思政建设指导纲要》指出，理学类课程，要在课程教学中把马克思主义立场观点方法的教育与科学精神的培养结合起来，提高学生正确认识问题、分析问题和解决问题的能力;要注重科学思维方法的训练和科学伦理的教育，培养学生探索未知、追求真理、勇攀科学高峰的责任感和使命感[3]。根据该指导思想，本研究挖掘出课程与思想政治教育的结合点（见表2）。

2. 开展课程思政教学的着手点

（1）通过数学家面对数学发展的三次危机的态度教育学生学习科学家精神。数学发展的三次危机的解决，可以让学生懂得危机与机遇并存，只要坚定科学的理念、正确的方法，就可能迎来更大的发展。

（2）利用数学史激励学生的民族自豪感和责任感，增强大学生的民族凝聚力。我国古代和现代数学的辉煌成就可激发学生的民族自豪感和学生强烈的民族责任感。

（3）将数学领域的最新动态引入课堂。比如2018年菲尔兹奖和阿贝尔奖双料得主迈克尔·阿提亚爵士宣称自己证明了黎曼猜想。黎曼猜想的内容是关于黎曼Zeta函数的零点分布问题，课程在绝对收敛性举例时刚好定义了Zeta函数。89岁高龄的迈克尔·阿提亚爵士早已功成名就，却还在挑战世界难题，虽然他的证明最终没有被数学界广泛认可，但是他的精神非常可贵。教师可引导学生通过这一案例找到让自己为之终身学习和努力的兴趣，并享受这个过程。

（4）为强调逻辑严谨性，可列举一些颠覆人们认知的悖论。一些结论在直观上是可行的，但是科学问题不能只靠感觉。比如教师可以通过轮子悖论的动画演示，让学生切身感受到“眼见不一定为实”的道理，进而强调作为大学生要有严谨治学的态度，要承认或使用一个结论，必须在有严谨证明的前提下进行。

（5）通过与课程内容相关的生活实例，帮助学生形成科学的世界观。在介绍傅里叶级数引论时，教师可以通过生活中一些直观形象、生动有趣的例子，向学生介绍傅里叶级数在生活中的应用[4]。

（6）通过讲解数学知识在生产、生活中的重要应用，帮助学生树立学好数学的决心。在微分方程引论中，教师可以通过介绍微分方程在海王星的发现、马王堆一号墓年代的确定、火箭发射以及传染病模型中的应用[5-6]，让学生了解微分方程的强大作用，了解祖国的强大，从而激发学生的爱国热情。

三、课堂教学案例展示

本研究以收敛级数的定义及通用判定准则为课堂教学案例。

（一）教学方案设计

1. 教学内容和目标

该课程主要讲授收敛级数的定义及基本性质，希望学生通过本节课的学习，理解收敛级数的定义，了解级数的早期发展情况以及学习级数的用处，注意验证级数收敛性的重要性，掌握判断级数收敛的几种通用准则。

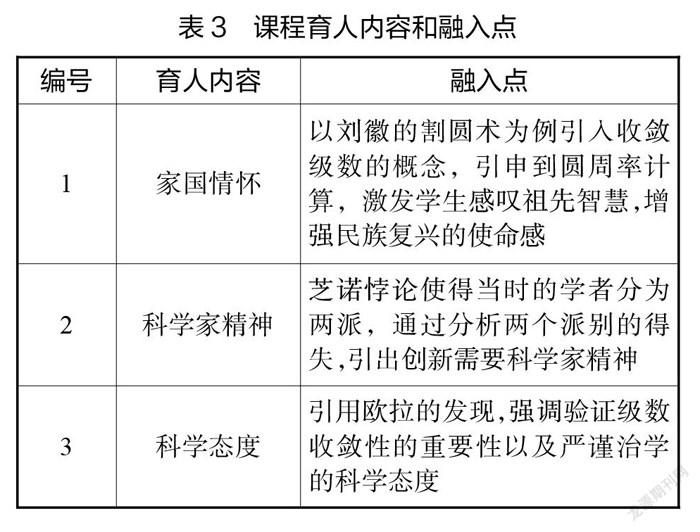
2. 课程育人内容和融入点

本节课的育人内容主要有：家国情怀、科学家精神以及科学态度三个方面。具体融入点见下表：

（二）思政元素的具体融入过程展示

1. 家国情怀

用我国古代刘徽的割圆术来引出收敛级数的定义。教师可从割圆术进一步延伸到圆周率的计算，向学生介绍我国的祖冲之算出的圆周率的精度领先了西方近1000年，使得中国在圆周率计算方面早早地走在了世界的前列，提升学生的民族自豪感。

接着，教师可以强调实现民族复兴，一定要靠科技进步，而科技进步的主力军还是要靠年轻的一代，通过这部分内容的融入，可以提升学生建设祖国的责任感和使命感。

2. 科学家精神

在给学生介绍无穷级数发展史的过程中，针对最早出现的级数形式——几何级数，教师可以讲解阿基里斯追龟的悖论。接着，介绍芝诺悖论引发的数学危机：当时芝诺提出的几个悖论使众学者被分成了两派：一派停滞不前，另一派积极攻克难题。借此机会，教师引出科学家们勇攀高峰、敢为人先的创新精神。《逆商》的作者把人生比作登山，把登上的人分成三类：放弃者、扎营者和攀登者[7]。通过分析这三类人的本质特点，学生很容易知道自己该做出何种选择。

3. 严谨治学的科学态度

介绍完收敛级数的定义后，教师要向学生强调验证级数收敛性的重要性。这部分可以通过数学家欧拉发现的一个反例来引起学生的重视，此时教师可以很自然地提出要求：大学生必须要有严谨治学的科学态度。

四、思政教学效果反馈

通过对授课班级发放问卷，本研究发现学生对于数学文化部分内容的接受度是令人满意的。大部分学生认为课堂上这方面内容对他们起到了价值引领的作用。而且，从数学文化的角度在课堂上融入思政元素基本达到了润物细无声的效果。

五、结语

当前，“高等数学（6）”被认定为校级课程思政精品示范课。希望通过不断地改革，能够使学生认识到数学的重要性，感受到学习数学的乐趣，具备一定的“数学素养”，也希望最大程度地實现高等数学课的育人功能。

参考文献：

[1] 齐民友. 《数学与文化》[M]. 大连：大连理工大学出版社，2008：1-302.

[2] 顾沛. 《数学文化》（第二版）[M]. 北京：高等教育出版社，2017：1-237.

[3] 中华人民共和国中央人民政府. 教育部高等教育司负责人就《高等学校课程思政建设指导纲要》答记者问[EB/OL].  （2020-06-06）. http：//www.gov.cn/zhengce/2020-06/06/content_5517612.htm.

[4] 如何直观形象、生动有趣地给文科学生介绍傅里叶变换？[Z/OL]. （2017-03-25）. https：//www.zhihu.com/question/1999102 6/answer/15640992.

[5] 陈华平，毕迎鑫. 浅析“常微分方程”课程教学中的思政教育[J]. 科技文化，2020（34）：111-112.

[6] 周霞，刘期怀，王先超. 新工科背景下以OBE为导向的常微分方程课程教学改革[J]. 阜阳师范大学学报（自然科学版），2020，37（04）：108-111.

[7] 保罗·史托兹. 逆商[M]. 北京：中国人民大学出版社，2019.

（责任编辑：胡甜甜）