钢箱梁截面有效分布宽度的计算分析

张静元，栾舒茗，聂玉东

(1.黑龙江省公路勘察设计院，黑龙江 哈尔滨 150000；2.黑龙江省公路桥梁勘测设计院有限公司，黑龙江 哈尔滨 150000)

1 概述

进行钢箱梁桥设计时首先要确定桥梁截面布置型式。钢箱梁的截面设计要充分考虑翼缘有效分布宽度,尽可能使截面翼缘受力时全宽有效,减小剪力滞效应对翼缘板应力计算结果的影响[1]。钢箱梁截面单箱宽跨比不宜过大,否则截面不经济,容易造成钢材浪费。以跨径30 m～50 m的多跨连续钢箱梁桥为例,对钢箱梁截面有效分布宽度进行分析研究。

2 钢箱梁截面有效宽度计算

JTG D64—2015公路钢结构桥梁设计规范(以下简称“规范”)[2]的5.1.8条第2款规定,箱形梁桥的翼缘有效分布宽度可以用式(1)和式(2)来计算:

(1)

(2)

以上公式中,式(1)适用于简支梁和连续梁的正弯矩区翼缘有效分布宽度计算,式(2)适用于连续梁的负弯矩区翼缘有效分布宽度计算。

以30 m跨径多跨连续钢箱梁为例,计算不同的翼缘宽度取值时,翼缘的有效分布宽度。按“规范”表5.1.8,计算得到边跨中梁段等效跨径为24 m,中跨中梁段等效跨径为18 m,支点梁段等效跨径为12 m。再取不同的翼缘宽度值,代入式(1)，式(2),得到翼缘有效分布宽度,计算结果见表1。

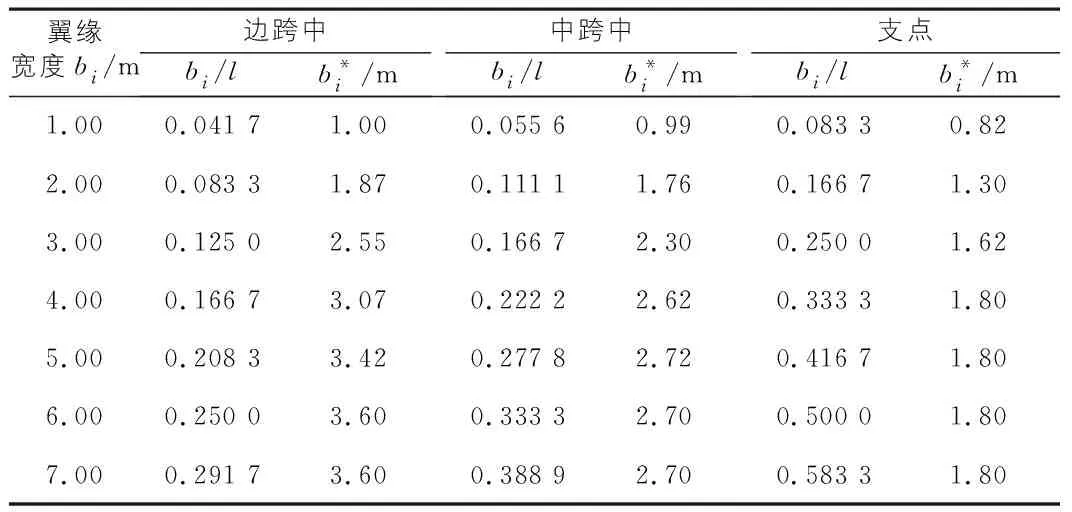
表1 跨径30 m连续钢箱梁翼缘有效分布宽度表

可以看出,对30 m等跨连续钢箱梁桥,其边跨正弯矩区截面的翼缘宽度小于2.0 m时接近全宽有效,翼缘宽度大于6.0 m时有效分布宽度基本不再变化,均为3.6 m;中跨正弯矩区截面的翼缘宽度小于2.0 m时接近全宽有效,而翼缘大于5.0 m时有效分布宽度不再变化,均为2.7 m;支点负弯矩区截面的翼缘宽度小于1.0 m时接近全宽有效,而翼缘大于4.0 m时有效分布宽度不再变化,均为1.8 m。对同一翼缘宽度值,边跨正弯矩区截面的有效分布宽度最大,中跨正弯矩区的次之,支点负弯矩区的最小。

根据表1,可以得到30 m跨径连续钢箱梁翼缘宽度与有效分布宽度关系图,见图1。按同样的方法,得到40 m，50 m跨径连续钢箱梁翼缘宽度与有效分布宽度关系图,见图2，图3。综合来看,30 m跨度钢箱梁,当边跨中、中跨中、支点截面的翼缘宽度分别取值2 m，2 m，1 m时,截面接近全宽有效,有效宽度比例为0.82～0.94;40 m跨度钢箱梁,当边跨中、中跨中、支点截面的翼缘宽度分别取值3 m，2 m，1 m时,截面接近全宽有效,有效宽度比例为0.88～0.92;50 m跨度钢箱梁,当边跨中、中跨中、支点截面的翼缘宽度分别取值4 m，3 m，1 m时,截面接近全宽有效,有效宽度比例为0.90～0.91。截面接近全宽有效时翼缘宽度及有效宽度比例见表2。

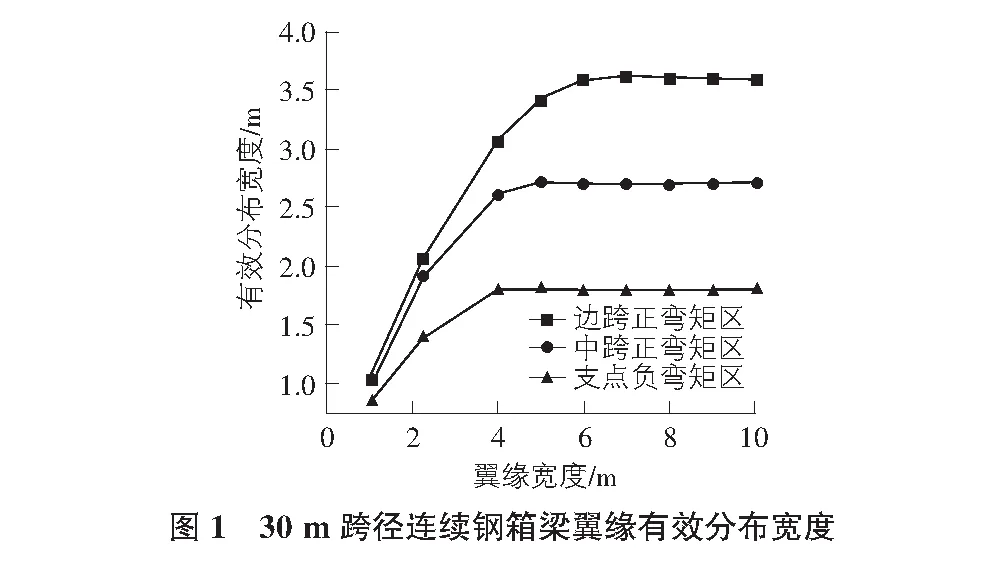
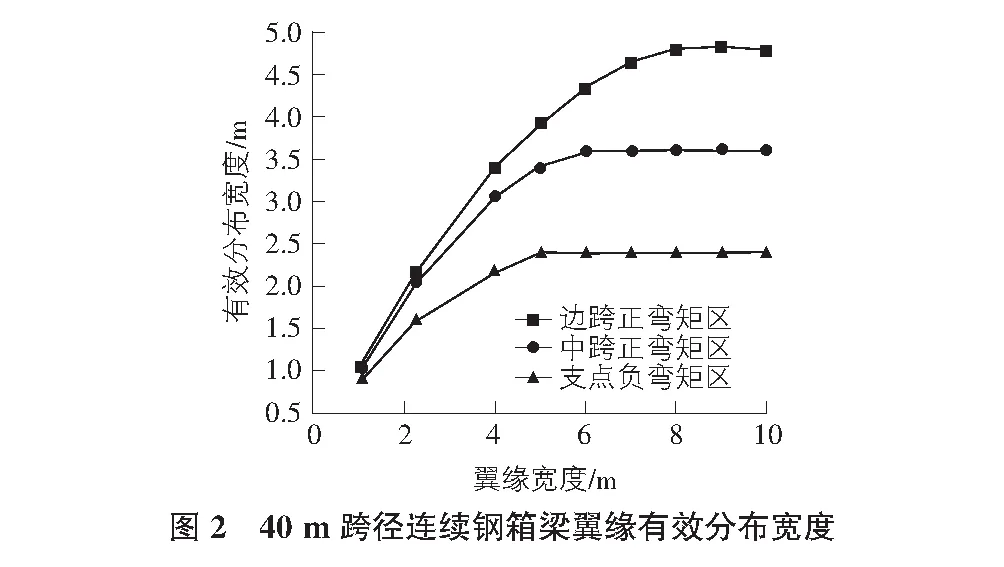
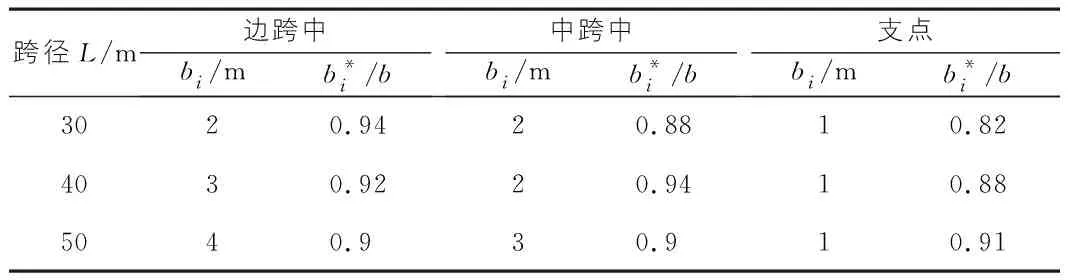
表2 翼缘宽度及有效宽度比例

3 有效分布宽度与跨径关系

对翼缘宽度为1.0 m钢箱梁连续梁(单箱宽2.0 m),计算不同跨径时翼缘有效宽度,结果见表3。可以看出,边跨跨中区、中跨跨中区及支点区这三个分区中,支点区截面的有效分布宽度最小,起控制设计作用。对支点区截面来说,当钢箱连续梁跨径为20 m时,翼缘有效分布宽度0.73 m,随着跨径增大,翼缘有效宽度增加,到跨径120 m时,翼缘有效分布宽度1.0 m,为全截面有效。若认为有效宽度比例达到0.90以上时为接近全截面有效,那么对单箱宽2.0 m钢箱梁连续梁,跨径达到45 m时,支点区截面接近全截面有效,但边跨跨中区、中跨跨中区,早已经全截面有效了。

表3 翼缘宽度为1.0 m时有效翼缘宽度

对截面单箱宽度为1.0 m，2.0 m，3.0 m，4.0 m，5.0 m，6.0 m钢箱梁连续梁,按以上计算方法,可得到有效宽度比例与跨径关系图,限于篇幅,仅列出单箱宽为2 m，4 m，6 m时的关系图,见图4～图6。

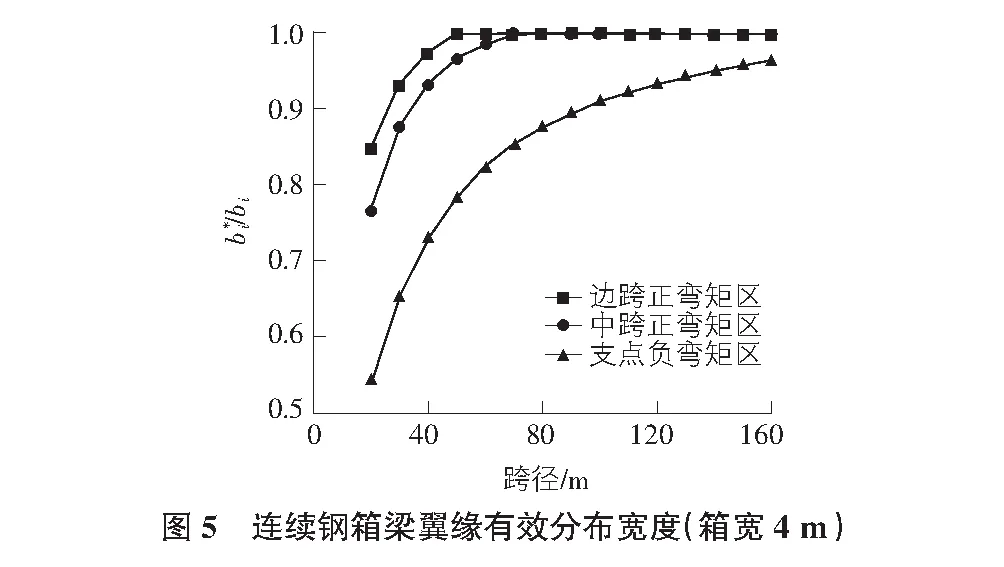
通过图4～图6,可以发现如下规律:

1)对支点区截面,当箱宽为1 m时,截面接近全截面有效时跨径(简称“理想最小跨径”)为23 m;当箱宽为2 m时,理想最小跨径为45 m;当箱宽3 m时,理想最小跨径为70 m;当箱宽4 m时,理想最小跨径为90 m;当箱宽5 m时,理想最小跨径为115 m;当箱宽6 m时,理想最小跨径为140 m。支点区截面箱梁宽度与连续梁跨径的关系可按式(3)确定。同理可得到适用于边跨跨中区和中跨跨中区的式(4)和式(5)。

2)为保证截面接近全截面有效,箱宽应与跨径对应,不宜偏大。例如,跨径90 m时,箱宽可取4.0 m,这时支点区截面接近全截面有效,有效宽度比例为0.9;如果跨径40 m时,箱宽仍然取4.0 m,这时支点区截面有效宽度比例为0.72,截面利用率较差。

3)最大箱宽Bmax(腹板间距)与跨径L关系可按下式计算(单位均为m)。

按支点区:

(3)

按边跨跨中区:

(4)

按中跨跨中区:

(5)

4 截面轮廓尺寸的确定

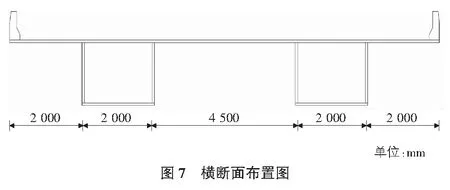
公路桥常用桥宽为12.5 m,这里对桥宽12.5 m的中等跨径钢箱连续梁,给出截面的轮廓布置。前面分析可知,对30 m～50 m跨径连续梁,钢箱梁单箱宽度在2.0 m左右时接近全宽有效,截面较为经济。另外,钢箱梁悬臂翼缘宽度宜取1.0 m～2.5 m,箱室左右翼缘板宽度对称。故将钢箱梁截面布置为双箱单室截面,单箱宽取2.0 m,外侧悬臂翼缘取2.0 m,内侧腹板相距4.5 m,横断面具体布置如图7所示。

5 工程实例

某公路桥梁采用跨径为(30+30+30)m连续的等截面钢箱梁为上部结构。桥梁横向全宽12.5 m,双向两车道。桥面横向布置为:0.75 m(防撞护栏)+11 m(行车道)+0.75 m(防撞护栏)。

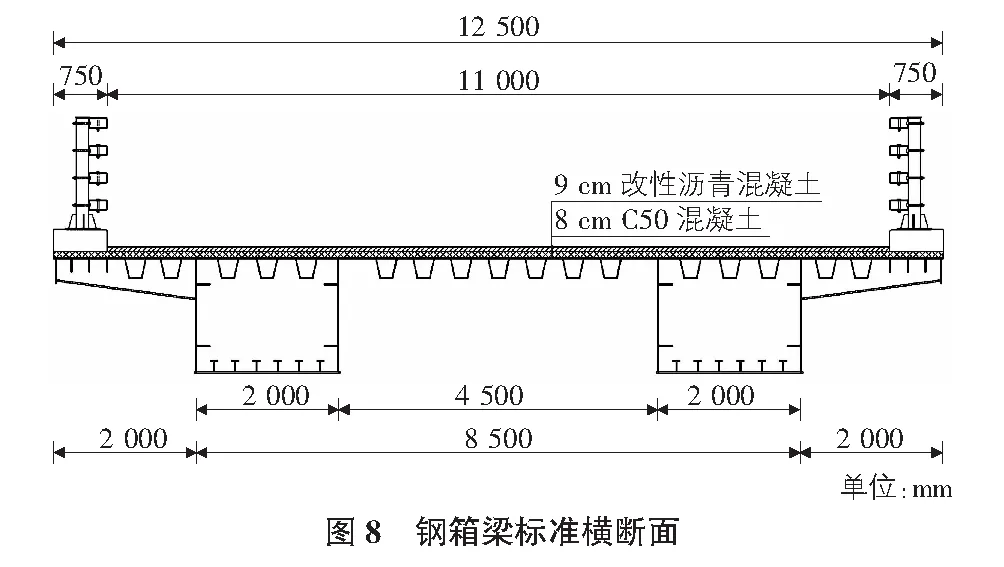
上部结构采用等截面钢箱梁,单箱单室,跨径30 m。箱梁梁高1.6 m;箱梁底板厚度支点附近取18 cm,跨中附近取16 cm;腹板厚度为14 cm,顶板厚度中支点附近取16 cm,跨中附近取14 cm。箱梁由2个单箱单室截面组成,箱梁顶宽12.5 m,单个箱室底宽2 m,箱间距4.5 m,悬臂端长2 m。2个箱室间设置横隔板连接,横隔板分为框架式横隔板和实腹式横隔板,各横隔板间距均为5.0 m,框架式横隔板和实腹式横隔板间距2.5 m交错布置;每个箱室内均设置横隔板,横隔板分为框架式横隔板和实腹式横隔板,各横隔板间距均为5.0 m,框架式横隔板和实腹式横隔板间距2.5 m交错布置;每个箱室内均设置腹板横向加劲肋;箱梁每个支点设置一道支点横隔板。顶板U形加劲肋板厚8 mm,I形加劲肋板厚18 mm;底板T形加劲肋板厚18 mm;顶、底、腹板等主要受力板件采用Q345qE钢材。钢箱梁横向设置2个支座,支座间距6.5 m。钢箱梁标准横断面如图8所示。

5.1 计算参数

1)恒载:钢材重度γ=78.5 kN/m3,桥面铺装采用9 cm改性沥青混凝土+8 cm C50混凝土。

2)自重系数:1.35。

3)活载:公路-Ⅰ级。

4)温度:按整体升温25 ℃、整体降温-45 ℃考虑;基于该桥的桥面铺装形式,梯度温差按JTG D60—2015公路桥涵设计通用规范[3]第4.3.12条取用,考虑钢箱梁顶板厚度范围内,正温差T1=14 ℃，T2=14 ℃,负温差T1=-7 ℃，T2=-7 ℃。

5)支座沉降:中支座不均匀沉降取10 mm,边支座取5 mm。

5.2 有限元模型建立

采用有限元程序建立结构模型,并以JTG D60—2015公路桥涵设计通用规范和JTG D64—2015公路钢结构桥梁设计规范为标准进行验算。有限元计算模型节点91个,单元90个,计算模型如图9所示。

5.3 钢箱梁计算结果分析

1)拉/压弯构件弯曲正应力验算。

根据JTG D64—2015公路钢结构桥梁设计规范第5.3.1条第1款的规定,桥梁钢结构构件的弯曲正应力应满足下式要求:

图4(a)和图4(b)分别逆变器桥臂上的主开关器件S1和S2进行状态切换过程中承受的电压uS1和uS2及所流经的电流iS1和iS2的实验波形，能看出S1和S2在开通过程中完成了零电压软开通动作，在关断过程中完成了零电压软关断动作.图4(c)和图4(d)分别为逆变器辅助开关Sa1和Sa4切换时端电压uSa1和uSa4及所流经的电流iSa1和iSa4的实验波形，可看出Sa1和Sa4在开通过程中分别完成了零电压软开通动作和零电流软开通动作，在关断过程中分别完成了零电压软关断动作和零电流软关断动作.

拉/压弯构件上缘弯曲正应力验算包络图如图10所示。

拉/压弯构件下缘弯曲正应力验算包络图如图11所示。

结论:按JTG D64—2015公路钢结构桥梁设计规范公式5.3.1-1,σ=218.53 MPa≤fd=270 MPa,满足规范要求。

2)剪应力验算。

根据JTG D64—2015公路钢结构桥梁设计规范第5.3.1条第2款的规定,桥梁钢结构构件腹板剪应力应满足下式要求:

γ0τ≤fvd。

剪应力验算包络图如图12所示。

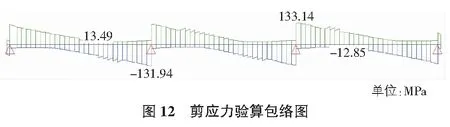
结论:按JTG D64—2015公路钢结构桥梁设计规范公式5.3.1-3,γ0τ=133.14 MPa≤fvd=155 MPa,满足规范要求。

根据JTG D64—2015公路钢结构桥梁设计规范第5.3.1条第4款的规定,受弯实腹式构件腹板在正应力σx和剪应力τ共同作用时,应满足下式要求:

折算应力验算包络图如图13所示。

结论:按JTG D64—2015公路钢结构桥梁设计规范,最大折算应力为231.89 MPa 小于折算应力容许值270 MPa,满足规范要求。

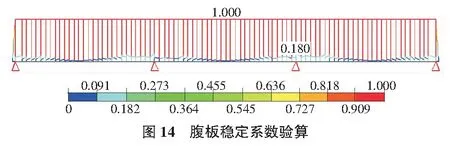
4)腹板稳定系数验算。

根据JTG D64—2015公路钢结构桥梁设计规范第5.3.3条第2款的规定,腹板的稳定应满足规范要求(见图14)。

5)疲劳验算。

按JTG D64—2015公路钢结构桥梁设计规范第5.5.4条规定,采用疲劳荷载计算模型Ⅰ时,应按下列公式验算:

Δσp=(1+Δφ)(σpmax-σpmin);

Δτp=(1+Δφ)(τpmax-τpmin)。

疲劳验算正应力幅图如图15所示。

按照JTG D64—2015公路钢结构桥梁设计规范第5.5.4条验算:疲劳正应力验算满足规范要求。

疲劳验算剪应力幅图如图16所示。

结论:按照JTG D64—2015公路钢结构桥梁设计规范第5.5.4条验算:疲劳应力验算满足规范要求。

6)变形验算。

按照JTG D64—2015公路钢结构桥梁设计规范第4.2条的规定,计算竖向挠度时,应按结构力学的方法并应采用不计冲击力的汽车车道荷载频遇值,频遇值系数为1.0。计算挠度值不应超过规范规定的限值。

按《公路钢筋混凝土及预应力混凝土桥涵设计规范》第6.5.3条验算:(不计冲击系数)频遇组合最大挠度设计值24.193 mm，不大于最大挠度允许值80 mm,满足规范要求。活载竖向位移如图17所示。

计算表明,钢箱梁的拉/压弯构件弯曲正应力验算、剪应力验算、折算应力验算、腹板稳定系数验算、疲劳验算、挠度验算均满足要求。

根据有限元计算结果可知,在考虑钢箱梁截面有效分布宽度条件下,根据钢箱梁截面单箱宽度与连续梁跨径的关系式拟定的钢箱梁截面尺寸满足受力要求。

6 结语

1)对同一钢箱梁,边跨正弯矩区截面的有效分布宽度最大,中跨正弯矩区的次之,支点负弯矩区的最小。2)对30 m～50 m跨径连续梁,钢箱梁单箱宽度在2.0 m左右时接近全宽有效,截面较为经济。3)为保证截面接近全截面有效,箱宽应与跨径对应,不宜偏大。4)钢箱连续梁截面单箱宽度与连续梁跨径关系可按式(3)～式(5)计算后综合确定。5)桥宽12.5 m、跨径30 m～50 m的中等跨径钢箱连续梁截面可采用单箱宽度2.1 m的双箱单室截面型式。